日本であまり知られていないタグチメソッド。その秘密と有用性に迫ります!
目次
タグチメソッドとは?
タグチメソッドとは田口玄一博士が考案した、研究開発や工程管理を効率的に行うための分野です。国内では品質工学と呼ばれています。また、米国などではタグチメソッドと呼ばれて親しまれています。
日本では当初それほど知名度は高くなかったのですが、米国では古くからタグチメソッドの名で親しまれ、多くの生産の現場を改善してきました。
実は世界各国の生産現場を支えているのが田口玄一先生の考案したタグチメソッドなのです!
その背景を経て、日本でも多くの生産現場で使われるようになってきました。しかし、未だにタグチメソッドを実際に取り入れている現場は少なく、リコール問題や品質問題など重大な問題があとを絶ちません。
戦後世界から絶賛された日本の品質の姿は取り戻すことができるのでしょうか
リコールが増えている?!
先ほど申し上げたように現在、日本ではリコール問題が増えています。
下の図は自動車のリコール台数を表したグラフで緑色のバーがリコール台数になります。
この数年で大きく増えていることが分かります。
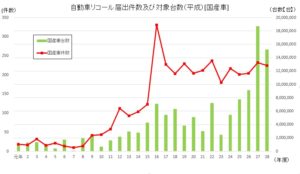
(出典:国土交通省 自動車局HP)
リコールが起きると消費者が被害を被るだけでなく、リコールをした企業に大きな負担がかかります。
最悪の場合、倒産というケースも免れないでしょう。
さて、このようなリコール問題や品質問題を防ぐために先程ご紹介したタグチメソッドが重要な働きをするわけですが、その働きを製品生産プロセスに焦点を当てて考えていきましょう。
製品を生産するプロセス
リコール問題は未然に防ぎたい!世の中に製品が出る前に防ぎたい!
製品生産プロセス
さて、製品を生産する時、どのようなプロセスがあるでしょうか。
①市場調査
②製品開発
③ライン設計
④材料調達
⑤プロトタイプ生産
⑥需要予測
⑦本製品生産
⑧出荷
細かく分けましたが、大きく分けると
①〜⑤で前段階の試作品を生産し改善
⑥〜⑧で実際の製品を生産していきます
①〜⑤の段階で品質を作り込む作業をタグチメソッドではロバストパラメータ設計と呼びます。
⑥〜⑧の段階で実際に工程管理を行い、異常な製品を弾きます。それをタグチメソッドではMTシステムと呼びます。
point!
タグチメソッドは大きく分けて2つ
・ロバストパラメータ設計
・MTシステム
それではこれらの説明にうつっていきましょう!
ロバストパラメータ設計
先程生産の過程で①〜⑤に当たるとご紹介したロバストパラメータ設計ですが、ここでいかに品質を作り込むかによって後々大きく変わってくるのでまず、このロバストパラメータ設計を理解し、実践することが大事です。
多くの生産の現場では、実際に作ってみてから問題があったら改善しようという怠惰な姿勢が散見されます。
例えば、あるモーターを生産する現場で不良が見つかりました。モーターのサイズの規格が製造工程で大きくなっています。
それではこの出力を調整し、モーターのサイズを規格内に抑えることが必要なのか。実はそうではない場合が多いのです。不良の原因は、目に見える出力ではなく、ノイズに対するロバストさの不足による原因が多いのです。
つまり、この場合、モーターのサイズの出力を調整したところで今度はモーターの騒音の規格が超えてしまうなどの別の不良が発生する可能性があります。
そのためタグチメソッドでは、まず、ノイズに対するロバストネスを高め、製品の入力に対する出力のばらつきを抑えた後に出力を調整します。
これによりリコール問題などの未然防止が可能になるのです
MTシステム
MTシステムは先程の製品生産のプロセスにおける⑥〜⑧の段階で用いられる手法群です。
MTシステムはマハラノビス・タグチシステムの略であり、田口先生がマハラノビス距離を用いて提案した各手法群という意味です。
MTシステムは大きく分けると異常検知・回帰に分かれ、その中でもいくつかの手法に分かれています。
・MT法
MTシステムの最も古い代表的な手法で、異常検知に用いられます。
一般的に正常状態は1つですが異常の状態は様々です。
そのため、ある状態を異常と固定し考えていると思わぬ落とし穴にハマり品質問題を起こしてしまうことになりかねません。
そこでMT法では単位空間とマハラノビス距離という概念を用いることで、より様々な異常原因に対応した異常検知が可能です。
以下が具体的な計算手順になります!
- 正常と分かっているp次元のデータ\({\bf x}_i,(i=1,2,\cdots,n)\)から標本平均ベクトル\(\hat{\mu}\)と標本共分散行列\(\hat{{\bf \Sigma}}\)を計算します。
\begin{eqnarray*}
\hat{\mu}&=&\frac{1}{n}\sum_{i=1}^n{\bf x}_i\\
\hat{{\bf \Sigma}}&=&\frac{1}{n}\sum_{i=1}^n({\bf x}_i-\hat{\mu})({\bf x}_i-\hat{\mu})^{T}\\
\end{eqnarray*} - 判別したいデータ\({{\bf x}’}\)の異常スコア\(d({{\bf x}’})\)を計算します。
\begin{eqnarray*}
d({{\bf x}’})&=&({{\bf x}’}-\hat{\mu})^{T}{\bf \hat{\Sigma}}^{-1}({{\bf x}’}-\hat{\mu})\\
\hat{{\bf \Sigma}}&=&\frac{1}{n}\sum_{i=1}^n({\bf x}_i-\hat{\mu})({\bf x}_i-\hat{\mu})^{T}\\
\end{eqnarray*} - \(d({{\bf x}’})\)がある閾値より小さければ正常、大きければ異常と判別します。
機械学習の各種異常検知手法に比べると検出力は弱いですが、もし仮に異常原因がわかっていない場合はMT法が圧倒的に有用となります。
より詳しいことが知りたい方はMT法のページを見てみてください!
・RT法
RT法はMT法の派生手法で比較的新しい手法となっております。
MT法では、サンプル数>変数でないとマハラノビス距離の逆行列が求められず、計算ができません。
それを可能にしたのがRT法です。
RT法では、主成分分析の第1主成分と残差の標準偏差を2つの変数として用います。
以下具体的な計算手順です!
- 正常だと分かっているデータを単位空間とします。単位空間のデータで項目ごとの平均と標準偏差を求めます。
\begin{eqnarray*}
m_j&=&\frac{1}{n}\sum_{i=1}^n{X_{ij}}\\
s_j&=&\sqrt{\frac{1}{n}\sum_{i=1}^n{(X_{ij}-m_j)}^2}\\
\end{eqnarray*} - 各サンプルにおいて各項目を並べたベクトルと各項目の平均を並べたベクトルをそれぞれ次のように表します。
\begin{eqnarray*}
{\bf x}_i&=&{(X_{i1},X_{i2},\cdots,X_{ip})}^T\\
{\bf m}&=&{(m_{1},m_{2},\cdots,m_{p})}^T\\
\end{eqnarray*} - 各サンプルで統計量\({Y}_{i1}\)と\({Y}_{i2}\)を求めます。
\begin{eqnarray*}
{Y}_{i1}&=&\frac{{\bf m}^T{{\bf x}_i}}{{\bf m}^T{\bf m}}\\
{Y}_{i2}&=&\sqrt{\frac{S_{ei}}{p-1}}\\
{S}_{ei}&=&{{\bf x}_i}^T{{\bf x}_i}-\frac{({\bf m}^T{{\bf x}_i})^2}{{\bf m}^T{\bf m}}\\
\end{eqnarray*} - \({Y}_{i1}\)と\({Y}_{i2}\)を用いて分散共分散行列\(V\)を求めます。
\begin{eqnarray*}
\bar{Y}_{1}&=&\frac{1}{n}\sum_{i=1}^n{Y_{i1}}\\
\bar{Y}_{2}&=&\frac{1}{n}\sum_{i=1}^n{Y_{i2}}\\
V_{11}&=&\frac{1}{n-1}\sum_{i=1}^n{(Y_{i1}-\bar{Y}_{1})^2}\\
V_{22}&=&\frac{1}{n-1}\sum_{i=1}^n{(Y_{i2}-\bar{Y}_{2})^2}\\
V_{12}&=&V_{21}=\frac{1}{n-1}\sum_{i=1}^n{(Y_{i1}-\bar{Y}_{1})(Y_{i2}-\bar{Y}_{2})}\\
V &=& \left(
\begin{array}{ccc}
V_{11} & V_{12} \\
V_{21} & V_{22} \\
\end{array}
\right)\\
\end{eqnarray*} - 分散共分散行列\(V\)の余因子行列\(A\)を求めます。
\begin{eqnarray*}
A = \left(
\begin{array}{ccc}
V_{22} & -V_{12} \\
-V_{21} & V_{11} \\
\end{array}
\right)\\
\end{eqnarray*} - 各サンプルのマハラノビス距離の2乗を求めます。
\begin{eqnarray*}
D_{i}^2&=&\frac{1}{2}(Y_{i1}-\bar{Y}_{1},Y_{i2}-\bar{Y}_{2})A
\left(
\begin{array}{ccc}
Y_{i1}-\bar{Y}_{1} \\
Y_{i2}-\bar{Y}_{2} \\
\end{array}
\right)\\
\end{eqnarray*}
さて、この解析手順を見ると元々はp次元あったデータを2つの統計量に要約してからマハラノビス距離を算出しています。
これが長所の理由です。
これにより高次元の場合にも解析のできる非常に有用な手法となっています。
より詳しいことが知りたい方はRT法のページを見てみてくださいね!
・T法
T法は回帰に用いられる手法です。
説明変数を目的変数から推定する逆回帰というテクニックを用いて解析を行います。説明変数の数に依存しないため変数>サンプル数の状況下でも計算可能となっております。重回帰分析と比較されることの多い手法です。
試作品を作った段階ではサンプル数が多く取れません。その状況で説明変数と目的変数の関係を見たい時、従来の重回帰分析では説明変数を減らすしか方法がありませんでした。しかし、T法を使えば、多くの説明変数と目的変数の関係を小サンプルの状況で観測することができます。
以下具体的な計算手順です!
T法による解析の手順は以下の通りです。
- 学習データの中から目的変数が中位にあるデータを単位空間とします。学習データから単位空間の平均を引くことでデータの基準化を行います。
\begin{eqnarray*}
\bar{x}_{j}&=&\frac{1}{n}\sum_{i=1}^n{x^{unit}}_{ij}, \bar{y}=\frac{1}{n}\sum_{i=1}^n{y^{unit}}_{i}\\
X_{ij}&=&x_{ij}-\bar{x}_{j}, M_{i}=y_{i}-\bar{y}\\
\end{eqnarray*} - 比例定数\(\hat{\beta_j}\)とSN比\(\hat{\eta_j}\)を算出します。
\begin{eqnarray*}
\hat{\beta_j}&=&\frac{\sum_{i=1}^lX_{ij}M_i}{r}\\
\hat{\eta_j}&=&\frac{\frac{1}{r}(S_{\beta_j}-V_{e_j})}{V_{e_j}}\\
r&=&{\sum_{i=1}^lM_{i}^2}\\
S_{T_j}&=&{\sum_{i=1}^lX_{ij}^2}\\
S_{\beta_j}&=&\frac{(\sum_{i=1}^lX_{ij}M_i)^2}{r}\\
S_{e_j}&=&S_{T_j}-S_{\beta_j}\\
V_{e_j}&=&\frac{S_{e_j}}{l-1}\\
\end{eqnarray*} - 逆推定をすることで各説明変数に対する目的変数の推定値\(\hat{M}_{ij}\)を求めます。
$$\hat{M}_{ij}=\frac{X_{ij}}{\hat{\beta_j}}$$ - 各説明変数に対する目的変数の推定値\(\hat{M}_{ij}\)をSN比\(\hat{\eta_j}\)によって重み付け総合をして基準化済みの総合推定値\(\hat{M}_{i}\)を算出します。
\begin{eqnarray*}
\hat{M}_{i}&=&\frac{1}{\sum_{j=1}^p\hat{\eta}_j}{\sum_{j=1}^p{\hat{\eta}_j\hat{M}_{ij}}}\\
\end{eqnarray*} - 単位空間の平均を加えることで基準化前の総合推定値\(\hat{y}_{i}\)を求めます。
\begin{eqnarray*}
\hat{y}_{i}&=&\frac{1}{\sum_{j=1}^p\hat{\eta}_j}{\sum_{j=1}^p{\hat{\eta}_j\hat{M}_{ij}}}+\bar{y}\\
\end{eqnarray*}
単位空間の標準化の仕方によって派生手法であるTa法やTb法なども提案されています。
T法に関してはこちらに詳しくまとめていますのでご参照ください。
より詳しいことが知りたい方はT法のページを見てみてくださいね!
まとめと書籍
いかがだったでしょうか。
タグチメソッドはあまり知られていない考え方かもしれませんが、世界中の品質を支える大切な手法です。
今後さらにタグチメソッドが多くの現場で使われるようになり、日本そして世界の品質・生産の現場が良くなることを願っています。
ちなみにタグチメソッドを勉強する上で有用な書籍を以下に取り上げておきますので良かったらご覧ください。
タグチメソッド入門
非常に簡単にタグチメソッドについて述べられています。
分量も少なくスラスラ読めると思うので初めてタグチメソッドを勉強するという方はまず読んでみると良いと思います。
入門タグチメソッド
先程の「タグチメソッド入門」じゃ物足りないよという人にはこちらの本をおすすめします。
タグチメソッドの背後にあるアルゴリズムや式構造を理解することができると思います。
入門MTシステム
上記の2つだと、ロバストパラメータ設計についてはある程度理解が進むと思いますが、MTシステムに関して深く知りたい方はこちらを読んでみることをおすすめします。

























