実データにつきものなのが、データの欠損。
そのようなデータを欠損データとか欠測データとか言ったりしますが、この記事では欠損データで統一します。
欠損データをそのまま分析してしまうと様々な不都合が生じます。
そこでこの記事では、そんな欠損データへの対応方法を徹底的にまとめていきます!
最後には、Pandasでの実装やオススメの本を紹介していきますよ!
ちなみに以下のYoutube動画で詳しく解説していますので是非こちらも参考にしてみてください!
目次
欠損データとは?

欠損データとはデータの一部が何かしらの理由によって取得できなかったデータのことを言います。
例えば、「毎日の売り上げデータがあったとしてパソコンの故障である日のデータが消えてしまった!」なんてことになると欠損データになります。
データに欠損があると通常の回帰分析などをしようとしてもそのままでは解析出来ないので何かしらの対応をする必要があります。
決定木系のツリーモデル(XGBoost、LightGBM、ランダムフォレスト)では欠損値があっても分析が出来ますが、やはり欠損値があると正しい評価が出来ない可能性があります。
表:欠損データ
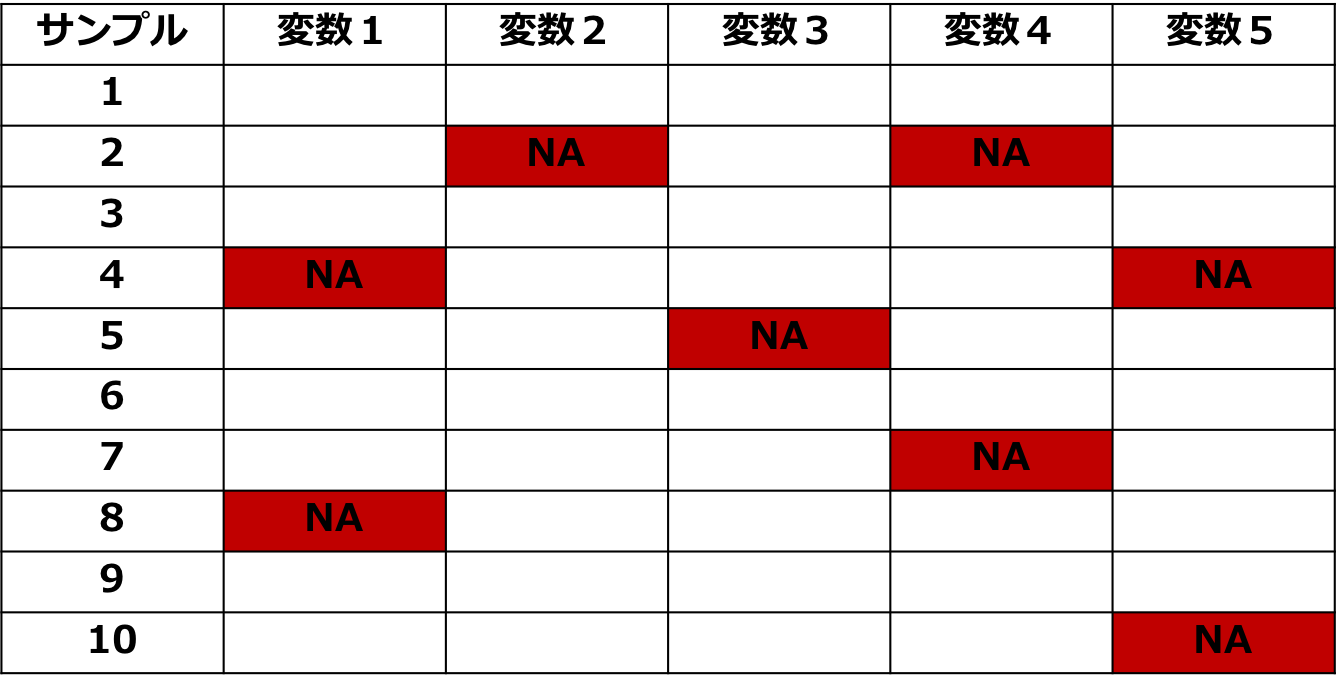
欠損データの扱いには二つの重要なポイントあります。
・欠損メカニズム
・解析のための処理方法
解析したいデータの欠損メカニズムを把握して適切な処理をしないと結果に偏りが出るおそれがあります。
欠損値の発生メカニズム
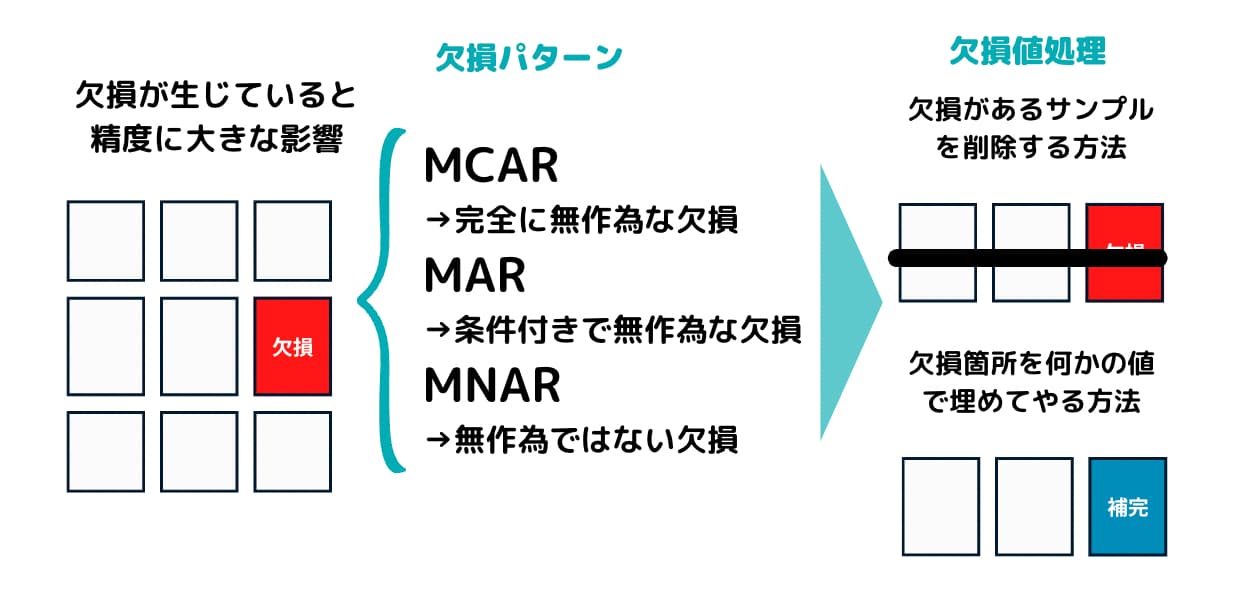
欠損メカニズムとはLittleさんとRubinさんによって提唱されたなぜ欠損をするのかを考えたものです。
メカニズムの種類によって欠損は「無視可能」と「無視不可能」に分類されます。
無視可能とは「欠損データの解析結果ともし欠損していなかった場合の完全なデータの解析結果との間に違いがない」ことを言います。
このように重要である欠損メカニズムは三つに分類されます。
MCAR
一つ目は完全に無作為な欠損という意味でMissing Completely At Randomの略で「MCAR」と呼びます。
これはある値の欠損する確率がデータと全く関係がない、完全にランダムに欠損することを言います。
先のデータでいうと体重を測ってもらう人ごとにサイコロを振ってもらって1が出たら体重を計らないとすれば欠損はMCARになります。
この欠損は常に無視可能です。
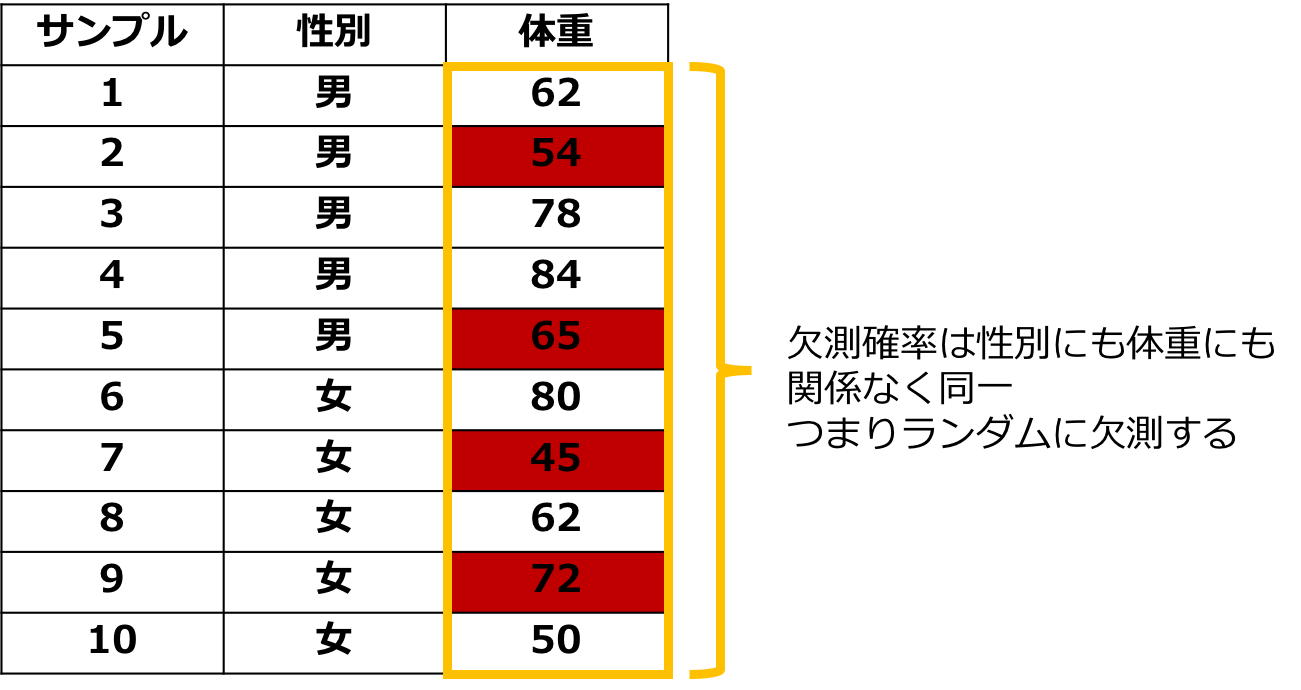
図:MCARのイメージ
MAR
二つ目は条件付きで無作為な欠損というものでMissing At Randomの略で「MAR」と呼びます。
これは、ある値が欠損する確率が観測されたデータで条件づけるとランダムになることを言います。
先のデータでいうと、男性と比べて女性の方が体重を計りたくないと考えるので性別によって欠損確率が変わります。
しかし、女性だけに絞ると欠損はランダムと考えられるのでMARになります。
欠損がMARの場合は欠損が存在するサンプルを削除して分析をすると推定結果が偏ることがあるので適切に処理する必要があります。
MARの場合でも無視可能とすることが多いです。
実際のデータでは欠損はMARの場合が多いです。
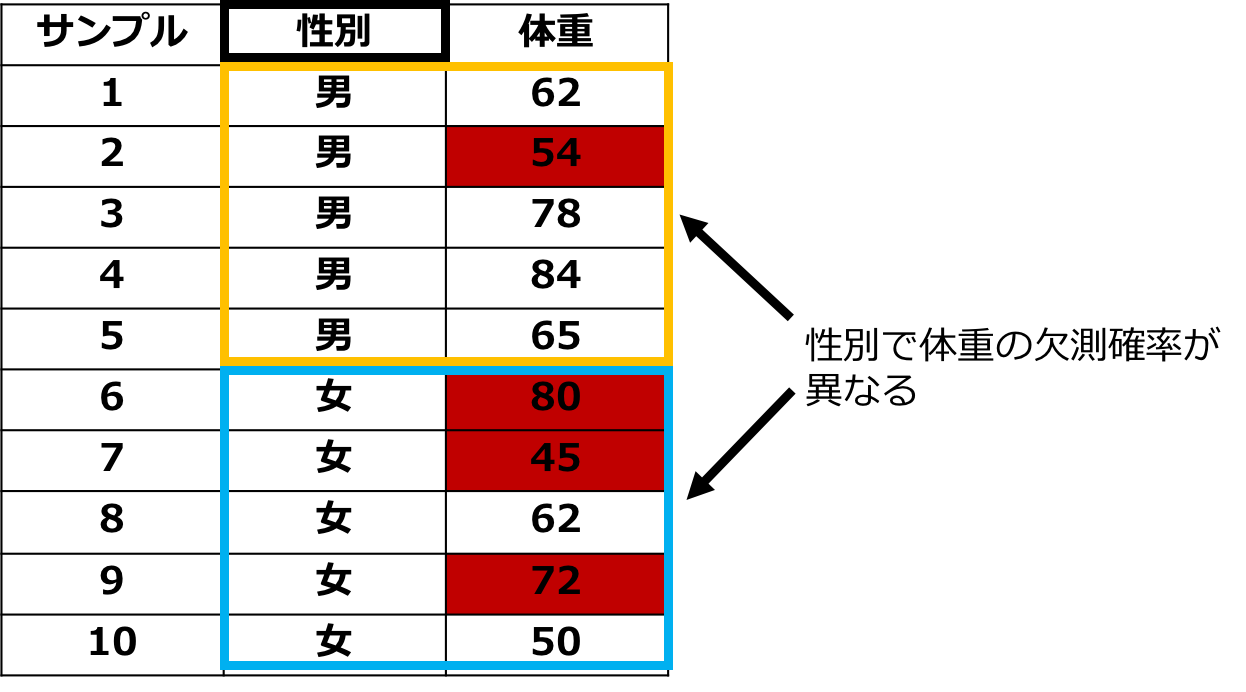
図:MARのイメージ
MNAR
三つ目は無作為ではない欠損というものでMissing Not At Randomの略で「MNAR」と呼びます。
これは、ある値が欠損する確率が欠損データ自体に依存していることを表します。
先のデータでいうと、体重が重い人ほど体重を計りたくないと考えると体重によって欠損確率が変わります。
データの中に体重を予測できる情報がなければ欠損は無視不可能になります。
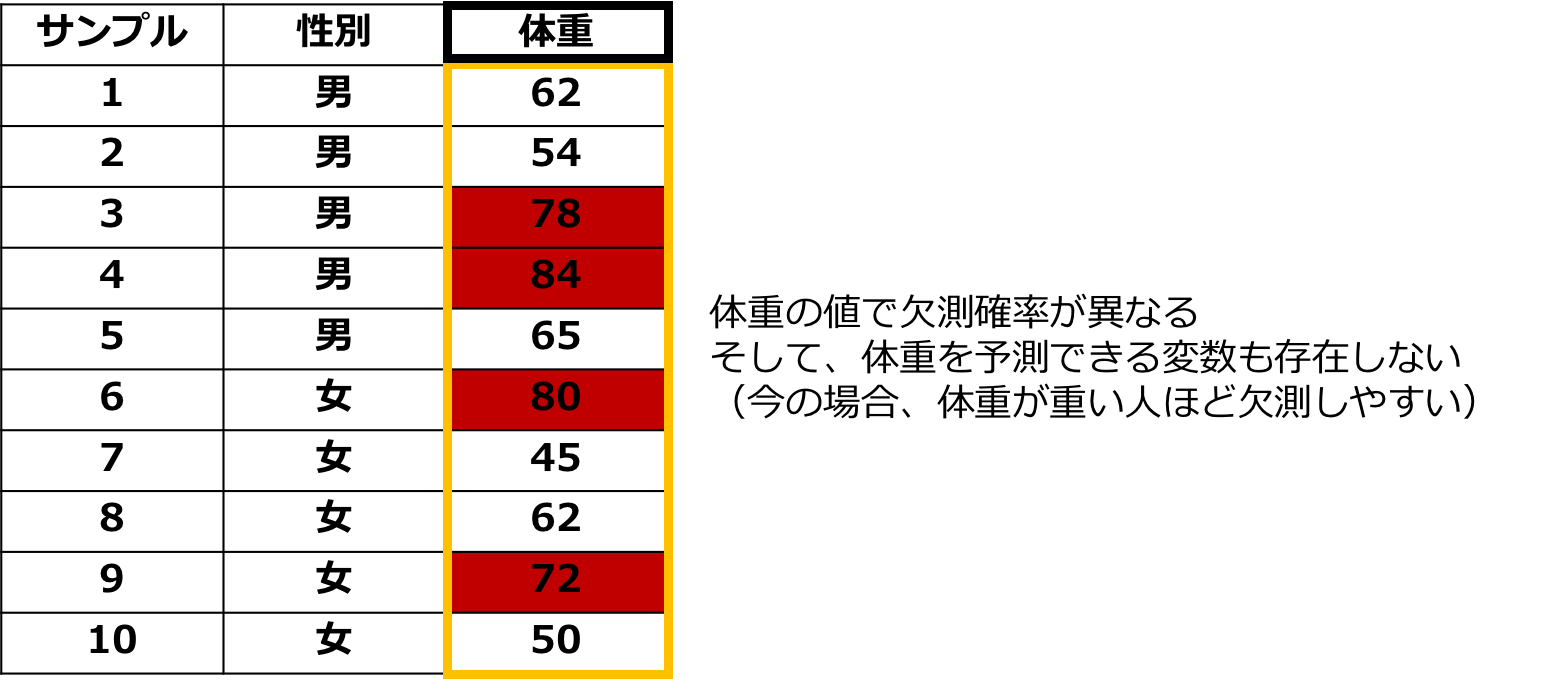
図:MNARのイメージ
欠損値の処理方法

処理方法はざっくり三つに分けられます。
欠損があるサンプルを削除する方法
最も単純なのは各サンプルで欠損が発生しているのであればそのサンプルを削除してしまう方法があります。
削除して完全なデータにしてから回帰分析などの解析を行います。
これはリストワイズ法と呼ばれます。
リストワイズ法は欠損がMCARであれば推定結果は不偏ですがMARの場合には偏りが出ることがあります。
また、サンプルを削除するので解析するときに推定効率が下がるなどの問題も起こりかねません。
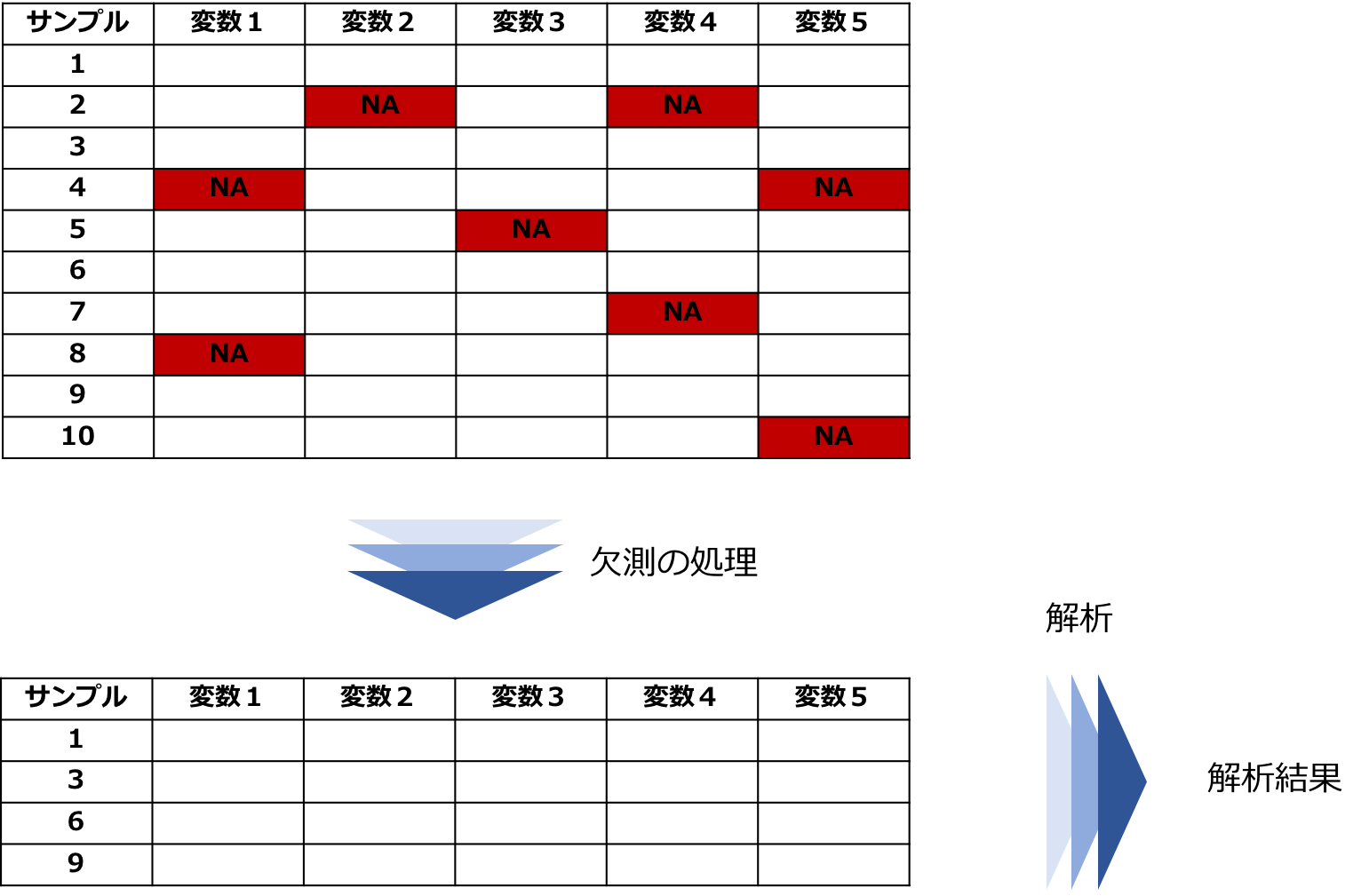
図:リストワイズ法での処理と解析
欠損箇所を何かの値で埋めてやる方法
二つ目は欠損箇所を何かの値で埋めてやる方法で代入法あるいは補完法と呼ばれます。
欠損部分に何かの値を代入することで完全なデータにしてから回帰分析などの解析を行います。
欠損がMARの場合でも代入法だとリストワイズ法のような問題が起きません。
代入法には単一代入法と多重代入法に分けられます。
単一代入法
これは一つの欠損部分に一つの値を代入する方法です。
手法としては
・平均値代入法
・比率代入法
・回帰代入法
・確率的回帰代入法
・ホットデック法
などがあります。
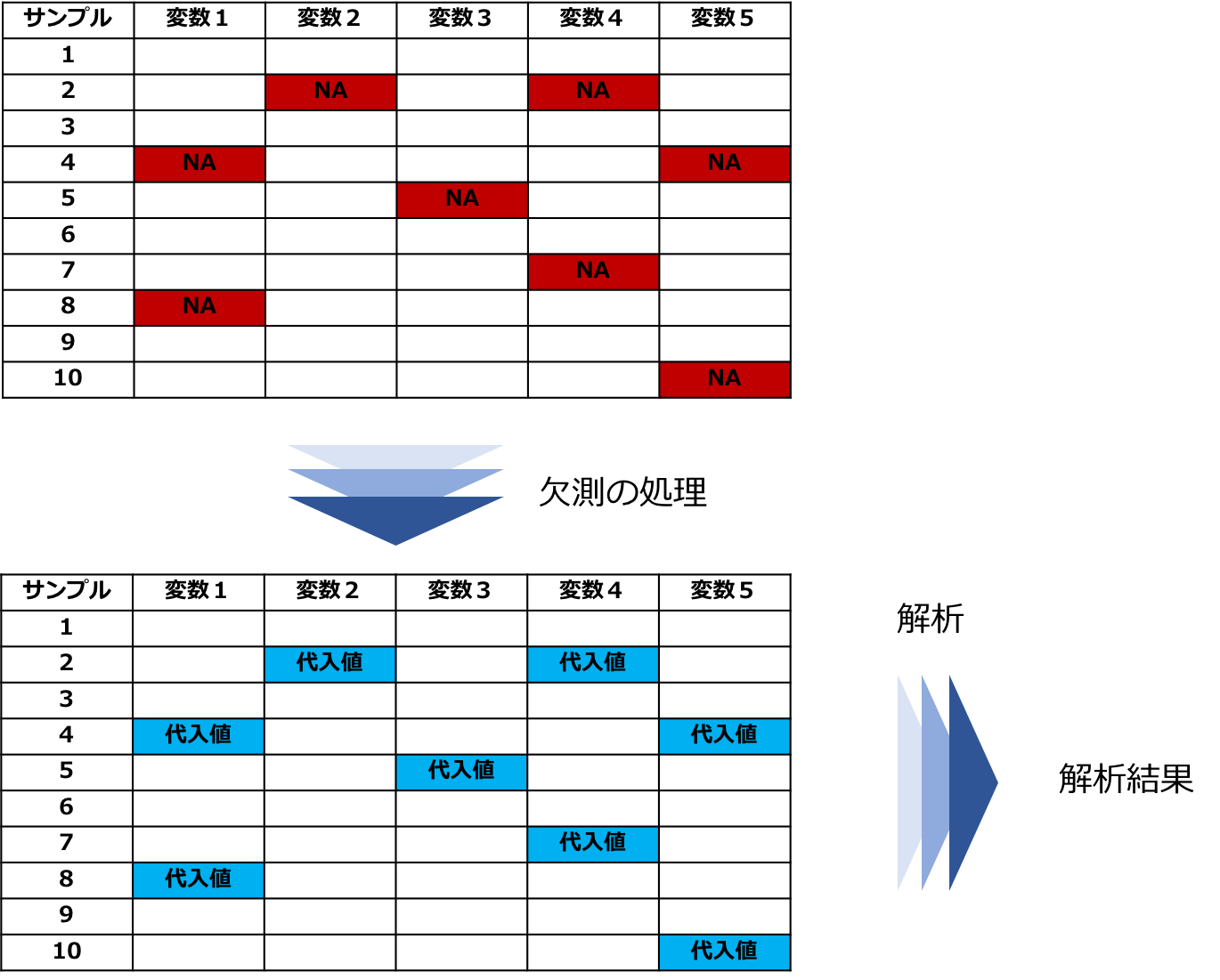
図:単一代入法での処理と解析
多重代入法
これは一つの欠損部分に複数の値を代入する方法です。
単一代入法では代入に用いるモデルが一つだけであり代入のためのモデルのばらつきを評価できていません。
そこで考えられたのが多重代入法です。
欠損データの事後予測分布から無作為に抽出されたM個のデータセットそれぞれで代入を行い、その後それぞれのデータセットで回帰分析などの目的としている解析を行います。
そして最後にM個の解析結果を統合することで最終的な解析結果とします。

図:多重代入法での処理と解析
欠損があってもそのまま解析する方法
三つ目は欠損があっても、統計モデルなどを仮定することで尤度に基づく解析方法があります。
手法としては
完全情報最尤推定法
などがあります。
欠損データをPandasで確認・補完してみよう!

最後に実際にカンタンな例を用いてPythonのPandasで欠損値の確認・補完をしていきます!
Pandasはデータ加工に便利なPythonのライブラリです。
ここでは実際にデータがあった方が分かりやすいので、Kaggleで有名なタイタニックのデータセットを使用します。
ちなみにpandasには既存のサンプルデータセットは入っていないのですが、seabornというライブラリを使えばサンプルデータセットを読み込むことが可能です。
タイタニックのデータであれば以下のように記述することで読み込みが可能。
import seaborn as sns
df = sns.load_dataset('titanic')タイタニックの生死データは非常に有名ですが、実は結構な欠損があるんです。
欠損値を確認してみましょう!
df.isnull().sum()によって各カラムの欠損値の数を集計することができます。
survived 0
pclass 0
sex 0
age 177
sibsp 0
parch 0
fare 0
embarked 2
class 0
who 0
adult_male 0
deck 688
embark_town 2
alive 0
alone 0
dtype: int64
続いて欠損値を処理する方法について見ていきましょう!
df.dropna()dropnaを使うことで欠損値が1つでも入っている行を削除することができます。
処理後の行数を確認してみると、
df.dropna().shape(182, 15)
182行に減っていることが分かります。
元々は891行ありました。
fillna()を使うことで欠損値を埋めることができます。
df['age'].head(10)0 22.0
1 38.0
2 26.0
3 35.0
4 35.0
5 NaN
6 54.0
7 2.0
8 27.0
9 14.0
Name: age, dtype: float64
年齢の欠損値を埋めてみましょう!
df['age'].fillna(0).head(10)0 22.0
1 38.0
2 26.0
3 35.0
4 35.0
5 0.0
6 54.0
7 2.0
8 27.0
9 14.0
Name: age, dtype: float64
6行目を0で埋めることができましたね!
ここで平均値などを代入することもできます。
このようにPandasを使うことで簡単にデータの欠損値を補完することができるんです。
Pandasでの各種処理は以下の記事でまとめていますので是非参考にしてみてください!

欠損データのまとめとおすすめ参考書
欠損データについて見てきました!
最後に欠損データのおすすめ書籍を紹介しておきましょう!
なかなか欠損データについてまとめられた書籍は少ないんですが、以下の二冊は非常に分かりやすいので是非読んでみてください!
■欠損データの統計解析 (統計解析スタンダード)
欠損データの扱いを全体的に分かりやすくまとめています。
■欠損データ処理: Rによる単一代入法と多重代入法 (統計学One Point)
(2024/04/24 23:07:48時点 Amazon調べ-詳細)
欠損データの扱いの中でも代入法、特に多重代入法のやり方が詳しく分かりやすく書かれています。
Rのコードも載っているので実際に解析してみると理解が早く進みます。
以下の記事で統計学全般のオススメ書籍を紹介しているのであわせてご覧ください!

また機械学習やPythonについての勉強方法については以下の記事でまとめています!


ちなみに機械学習やPythonについて網羅的に学びたい方は当メディアが運営するAIデータサイエンス特化のスクール「スタアカ(スタビジアカデミー)」をチェックしてみてください!


























