統計学において頻繁に登場する有意差という概念。
実際にビジネスの現場で使われていることも多々ありますが、しっかりと有意差という概念に対して理解した上で使われているのか疑問に思うことがあります。
この記事では、そんな「分かっているようで意外と分かっていない有意差」に関して見ていきます。
有意差を含めた統計学全般について学びたい方は、ぜひスタビジアカデミーの統計学概要コースを覗いてみてください!
また統計学の基礎を学べるUdemy講座を以下で公開していますので是非見てみてください!
※Twitterにメンションいただければ講師クーポン発行可能です!
有意差とは
有意差とは何なのか??
動画でも解説していますよ!
コトバンクから有意差の意味を引っ張ってきました。
統計上、ある事柄の起こる確率が有意水準未満であること、つまり偶然であるとは考えにくいことをいう。(出典:コトバンク)
有意差という言葉をそのまま捉えると「意味の有る差」。
つまり、有意差があるかどうかを測るというのは、その事象には意味があるのかを測るということ。
偶然起きたのかそうでないのかを調べるのが「有意差」なのです。
有意差はどうやって見る?

それでは、そんな有意差はどのように見ていけばよいのでしょうか?
まずは、単純な検定で有意差を見ていきましょう。
検定を用いる状況として、例えばアイス製造会社を考えてみましょう。
この会社が製造しているバニラアイスの内容量は200mlに設定しているはずです。
ある日、社長が「200mlになっていない気がする」と生産管理の担当者に伝えました。そこで、生産管理の担当者であるAさんとBさんは本当に200mlになっているかどうかを確かめることにしました。
そして、製造した製品の中から無作為に10個ほど選んで内容量を測ったところ次のようになりました。
$$205,198,197,208,204,202,207,199,207,203 (ml)$$
このデータから平均値を計算すると\(\bar{x}=203\)でした。さて、設定は200mlからずれているのでしょうか。
ここで、用語を整理しておきます。
・母集団…ある傾向をもつアイスの集まり。(神にしか分からない)
・母数…母集団の特徴を定める傾向のこと。例えば、母平均や母分散。(神にしか分からない)
・標本…母集団から得られた観測値群のこと。今の場合、選んだアイス10個のこと。
・帰無仮説…何も違いがないという仮説。今の場合、「アイスの平均の設定が200mlでずれていない」ということ。
・対立仮説…何か違いがあるという仮説。今の場合、「アイスの平均の設定が200mlからずれている」ということ。
・棄却…帰無仮説を否定すること
検定では確率分布という道具を使います。
今の場合はアイスの平均に関する検定なので正規分布を用います。
また、簡単のために母分散は\(4^2\)と知っていることにしておきます。そうすると母集団は\(N(\mu,4^2)\)に従います。そして、問題は\(\mu\)が200であるのかどうなのかということです。
仮に、\(\mu=200\)であるとしましょう。
平均\(\bar{x}=203\)を正規化した\(u\)は\(N(0,1^2)\)に従います。
このとき、正規分布の確率密度関数から分布の端っこの面積が5%になる点はどこかを計算すると-1.960と1.960という値になります。
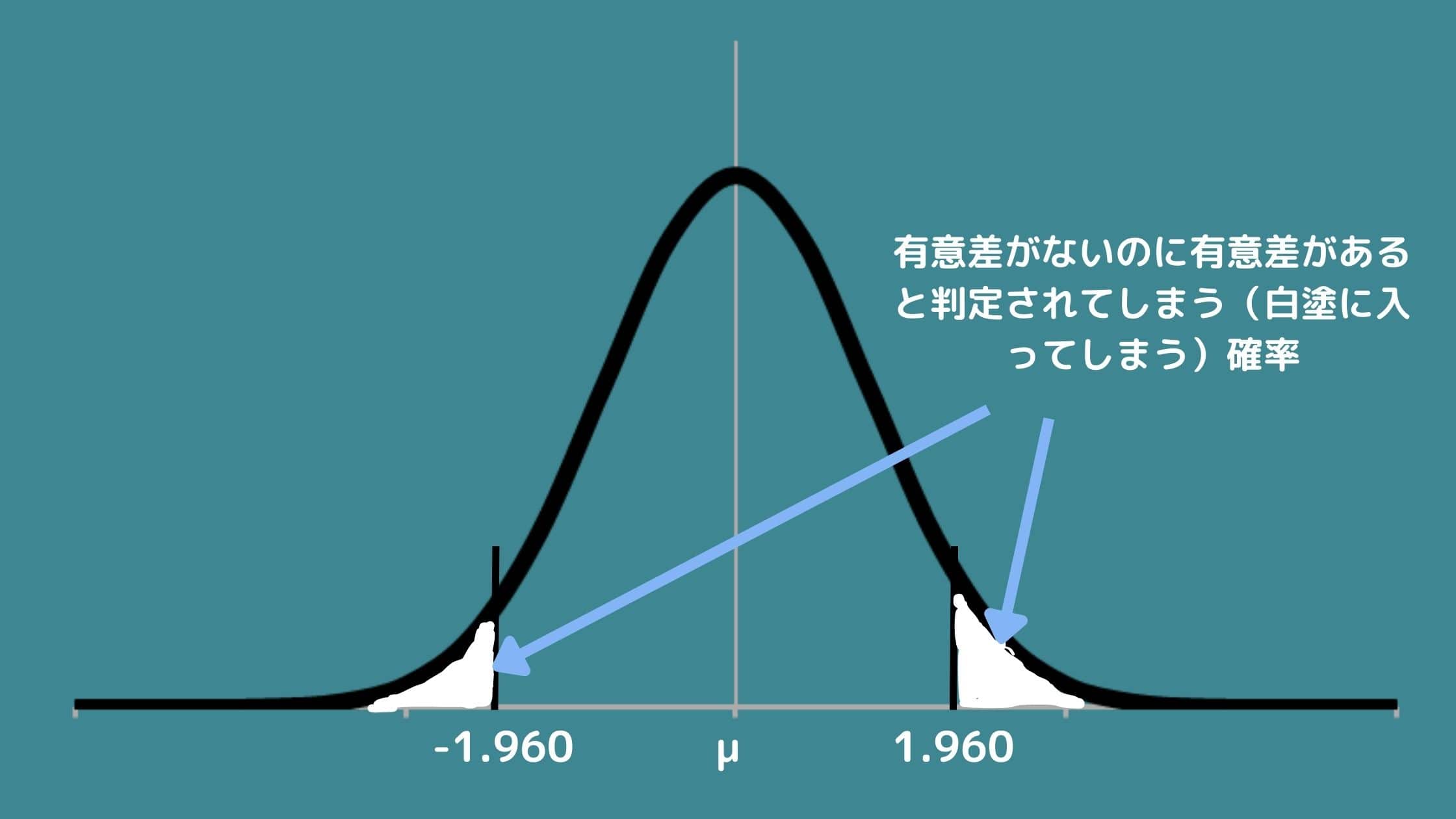
これはつまり\(N(0,1^2)\)に従うデータが「-1.960よりも小さい」あるいは「1.960よりも大きい」可能性が5%くらいしかあり得ないということを意味します。
さて、いま計算して\(|u|\)を求めると2.372という値になりました。この値は1.960より大きいです。
この結果の解釈は、
\(\mu=200\)と考えて、つまり、データが\(N(200,4^2)\)に従うと考えて計算した結果、たった5%も起こらないようなことになってしまったということ。
\(\mu=200\)つまり帰無仮説は間違っていたんじゃないの?というのが検定の論理なんです。
この5%というのは有意水準と呼ばれ、この5%を下回った場合に有意差があると言われるんです。有意水準は一般的に5%や1%が用いられます。
今回は母分散が既知であることにしていましたが、実際の場面では母平均が分からないのに母分散が既知であることは稀です。ってか普通ありえないですよね笑
そこで母分散も未知であるとして標本分散を用いて検定を行うのが通常です。そのような検定方法をt検定と呼び、最もよく使われるので覚えておくと良いでしょう!
検定に関してはこちらに詳しくまとめていますので良ければご覧ください!

この有意差は一見単純な検定だけに使われているように思われがちですが、統計学に関わる全ての手法に有意差の概念は組み込まれているのです。
例えば複数の説明変数と目的変数の関係を見る重回帰分析。
説明変数の選択には有意差の概念が組み込まれており、それぞれの変数が目的変数に寄与しているかどうかを帰無仮説、対立仮設を立てて有意水準を決め検定しているのです。
例えば「複数の説明変数の回帰係数は0である」と帰無仮説をおき、検定を行うことが挙げられます。
有意差のありがちな誤解

有意差についてある程度分かっていただけたと思いますが、ありがちな間違いがあるのでここで紹介しておきます。
先ほどの例で、\(|u|\)が1.960より小さい場合は\(\mu=200\)つまり帰無仮説が正しいと考えて良いのでしょうか?
実は対立仮設を棄却できたからと言って、帰無仮説が正しいとは言えないのです。
有意な差があるとは言えない、ということが分かっただけで有意な差がないとは言えないんです。
これはよく勘違いされている部分なので有意差を考える上で必ず覚えておきましょう。
有意差 まとめ
最後に有意差についてまとめておきましょう!
・ある事象が偶然起きたのかそうでないのかを調べることができるのが「有意差」
・有意差は回帰分析などの統計的手法に広く取り入れられている
是非有意差についてちゃんと理解して用いることで一歩進んだビジネスパーソンになりましょう!
有意差をはじめとした統計の基礎を理解するには以下の書籍がオススメです。
他にも統計学を勉強する上でオススメの本をこちらにまとめているのでよければご覧ください!

書籍で勉強するのはちょっと・・・という方は当メディア運営のスタアカ(スタビジアカデミー)で学んでみてください!
「統計学概要」というコースで、有意差を理解する上で重要な統計的検定について学びt検定やカイ二乗検定について手を動かして実装していきますよー!
スタアカ(スタビジアカデミー)
 公式サイト:https://toukei-lab.com/achademy/
公式サイト:https://toukei-lab.com/achademy/
| 【価格】 | ライトプラン:980円/月 プレミアムプラン:98,000円 |
|---|---|
| 【オススメ度】 | |
| 【サポート体制】 | |
| 【受講形式】 | オンライン形式 |
| 【学習範囲】 | データサイエンスを網羅的に学ぶ 実践的なビジネスフレームワークを学ぶ SQLとPythonを組み合わせて実データを使った様々なワークを行う マーケティングの実行プラン策定 マーケティングとデータ分析の掛け合わせで集客マネタイズ |
データサイエンティストとしての自分の経験をふまえてエッセンスを詰め込んだのがこちらのスタビジアカデミー、略して「スタアカ」!!
当メディアが運営するスクールです。
24時間以内の質問対応と現役データサイエンティストによる複数回のメンタリングを実施します!
カリキュラム自体は、他のスクールと比較して圧倒的に良い自信があるのでぜひ受講してみてください!
他のスクールのカリキュラムはPythonでの機械学習実装だけに焦点が当たっているものが多く、実務に即した内容になっていないものが多いです。
そんな課題感に対して、実務で使うことの多いSQLや機械学習のビジネス導入プロセスの理解なども合わせて学べるボリューム満点のコースになっています!
ウォルマートのデータを使って商品の予測分析をしたり、実務で使うことの多いGoogleプロダクトのBigQueryを使って投球分析をしたり、データサイエンティストに必要なビジネス・マーケティングの基礎を学んでマーケティングプランを作ってもらったり・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践してもらったりする盛りだくさんの内容になってます!
・BigQuery上でSQL、Google Colab上でPythonを使い野球の投球分析
・世界最大手小売企業のウォルマートの実データを用いた需要予測
・ビジネス・マーケティングの基礎を学んで実際の企業を題材にしたマーケティングプランの策定
・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践して稼ぐ
ちなみに自作の有意差算出Webアプリケーションを作ってみましたのでぜひ合わせてチェックしてみてください!