線形計画法の解法

線形計画法を解くためには、いくつかの主要な解法があります！

ここでは２つの変数を持つ線形計画問題に適用できる直観的な解法である「図式解法」と、許容解の空間を移動しながら最適解を探すアルゴリズムである「シンプレックス法」について説明します！

図式解法

まずは前のレッスンの製品の生産問題を例に、図式解法で最適解を求めていきます。

まずは制約条件をグラフにプロットしてみましょう！

3つの制約条件から1次方程式をグラフ化する要領で図示していきます。

２つの式と非負制約を基に、制約条件を満たす範囲をグレーで塗りつぶしたものは以下のようになります！

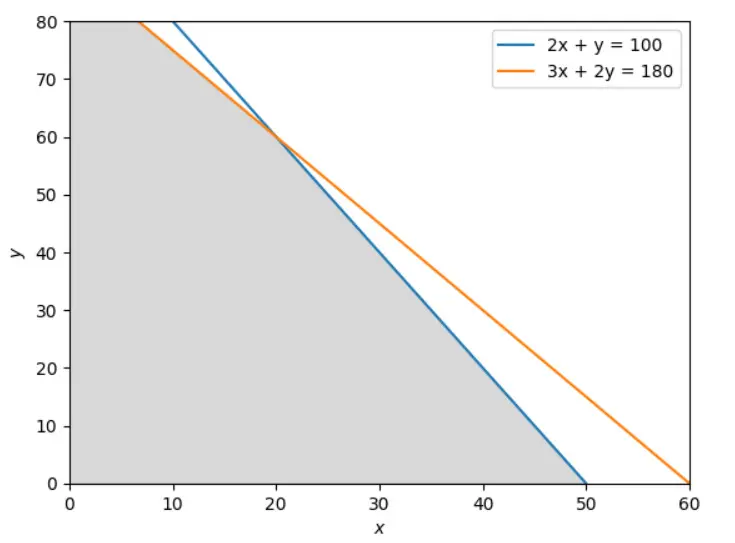
図式化が完了したら、実際に図から最適解になりそうなところを見ていきます！具体的には全部で4点あるグレーの制約条件の頂点に着目することで最適解を見つけることが出来ます！

大変申し訳ございませんが、y軸の切片は見切れております

それでは実際に以下の4つの頂点についてそれぞれ評価し、最大化していきたい合計利益を計算します！

・(0, 0)
・(50, 0)
・(0, 90)
・(20, 60)

2点目と3点目はそれぞれの1次方程式の切片です！

4点目についてはオレンジと青のグラフの交点であり、連立方程式を計算して求めましょう！

そして頂点の各点における目的関数の値は以下になります。

・(0, 0)：Z=40(0)+30(0)=0
・(50, 0)：Z=40(50)+30(0)=2000
・(0, 90)：Z=40(0)+30(90)=2700
・(20, 60)：Z=40(20)+30(60)=2600

最適解は、これらの頂点の中で目的関数の値が最大となる点です。

上記よりこの例では、(0, 90)が最適解でありZ=2700となります。

つまり、今回の例では、製品Aを1個も作らずに全て製品Bを生産するのが利益の面で最適解であるといった結果が確認できました！

続いて、シンプレックス法について簡単に説明します！

シンプレックス法は、線形計画法の中でも広く使用されていて、一言で表すと「許容解の空間を移動しながら最適解を探すアルゴリズム」となっています！

基本的な考え方

・初期の許容解を選定する。

・目的関数の値が改善する限り、隣接する許容解に移動していく。

・値の改善が見られなくなったら、その時点の解を最適解として終了。

実際のステップ

１．初期解の設定：開始点を設定する。

２．方向の選択：どの方向に移動するかを決定する。

３．ステップサイズの決定：どのくらい移動するかを決定する。

４．解の更新：新しい解に移動し、この流れを繰り返す。

実際には少し複雑な計算等も発生しますがここでは割愛します。

簡単ですがシンプレックス法についても紹介しました！

メリットしては、非常に高い精度で最適解を求めることができ、かつ効率的に解を求めることができる点が挙げられます！

反対にデメリットとしては、初期解の選択が適切でないと計算が非効率になる可能性がある点や、高次元空間での計算量が膨大になることがある点が挙げられるでしょう。

課題

前のレッスンで独自で設定した線形計画問題を図式解法で解いてみよう！