こんにちは！スタビジ編集部です！
線形計画法とは、ある目標を達成するために最適な方法を見つける数学の手法です。
例えば、限られた予算でお菓子をできるだけたくさん買いたいとき、どのお菓子を何個買えばいいか？を決定するのに使います！
目標（お菓子の数）と条件（予算）を数式にして、条件に合った最も良い答えを計算から導き出すのが線形計画法です！
今回はこの線形計画法について詳しく解説し、Pythonでの実装例も紹介していきます！
・線形計画法とはなにか
・線形計画問題の具体例
・線形計画法の複数の解法
・実際の応用事例
・Pythonでの実装
以下のYoutube動画でも解説していますのであわせてチェックしてみてください！
目次
線形計画法とは？
線形計画法は、多くの制約条件の下で最適な解を見つけるための強力な数学的手法です！
ビジネス、エンジニアリング、経済学など、さまざまな分野で広く利用されています。
例えば、限られたリソースを最も効率的に使って利益を最大化したり、コストを最小化したりする際に役立ちます！
ビジネスにおいては、生産計画、在庫管理、輸送問題などで頻繁に利用されます。
もう少し手法について細かく見ていきましょう。
線形計画法は、目的関数を最大化または最小化するための手法で、いくつかの線形な制約条件の下で行われます。
ここで、目的関数は最大化または最小化をしたい対象（例えば利益、コスト）を表し、制約条件は資源の制限や技術的な制約などを表します！
目的関数
最適化の対象となる関数。例えば、利益を最大化する場合の利益関数や、コストを最小化する場合のコスト関数。
例：利益=2x + 3y という式があった時にxとyの値を変えて利益を最大化することが目的。
制約条件
目的関数を最適化するために守らなければならない条件。これには資源の限界や技術的な制限が含まれ、通常、不等式や等式で表現される。
許容解
制約条件を満たす解。制約条件の範囲内で目的関数の値を計算できる解。
最適解
全ての許容解の中で目的関数の値が最も良くなる（最大または最小となる）解。
この最適解を見つけることが線形計画法の目的。
線形計画法問題の具体例
続いて、線形計画法の具体例についてわかりやすい例を取り上げて見ていきましょう！
製品の生産計画
ある工場では、製品Aと製品Bを生産しています。
それぞれの製品を生産するには異なる資源が必要であり、資源には限りがあります。
目標は、資源の上限という制約条件を満たしつつ、利益を最大化するために各製品をどれだけ生産するかを決定することです！
問題設定
問題設定は以下の通りです！
製品Bの利益：30ドル
製品Aを1個生産するのに必要な資源：2時間の労働力と3キログラムの原材料
製品Bを1個生産するのに必要な資源: 1時間の労働力と2キログラムの原材料
利用可能な労働力: 100時間
利用可能な原材料: 180キログラム
制約条件の設定と目的関数
上記の問題設定から、今回の生産計画を行う際の制約条件を式として表していきます！
今回は制約条件として以下の３つを設定する必要があるでしょう！
$$2x+y\leq100（労働力の制約）$$
$$3x+2y\leq180（原材料の制約）$$
$$x\geq0,y\geq0（非負制約）$$
ここで、xは製品Aの生産量、yは製品Bの生産量を表します。
実際に最適化の対象となる関数である「目的関数」は以下の式で表現することが出来ますね！
$$最大化Z=40x+30y$$
次の章では、こういった制約条件付きの目的関数を解くための解法についてご紹介します！
線形計画法の解法
線形計画法を解くためには、いくつかの主要な解法があります！
ここでは２つの変数を持つ線形計画問題に適用できる直観的な解法である「図式解法」と、許容解の空間を移動しながら最適解を探すアルゴリズムである「シンプレックス法」について説明します！
図式解法
まずは上記の製品の生産問題を例に、図式解法で最適解を求めていきます。
まずは制約条件をグラフにプロットしてみましょう！
3つの制約条件から1次方程式をグラフ化する要領で図示していきます。
２つの式と非負制約を基に、制約条件を満たす範囲をグレーで塗りつぶしたものは以下のようになります！
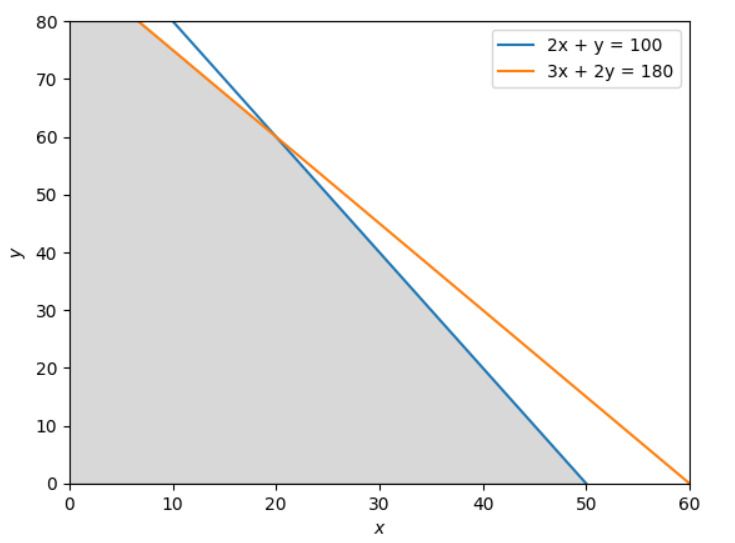
図式化が完了したら、実際に図から最適解になりそうなところを見ていきます！
具体的には全部で4点あるグレーの制約条件の頂点に着目することで最適解を見つけることが出来ます！（y軸の切片は見切れております）
それでは実際に以下の4つの頂点についてそれぞれ評価し、最大化していきたい合計利益を計算します！
- $$(0, 0)$$
- $$(50, 0)$$
- $$(0, 90)$$
- $$(20, 60)$$
2点目と3点目はそれぞれの1次方程式の切片です！
4点目についてはオレンジと青のグラフの交点であり、連立方程式を計算して求めましょう！
そして頂点の各点における目的関数の値は以下になります。
- $$(0, 0)： Z = 40(0) + 30(0) = 0 $$
- $$(50, 0)： Z = 40(50) + 30(0) = 2000 $$
- $$(0, 90)：Z = 40(0) + 30(90) = 2700 $$
- $$(20, 60)：Z = 40(20) + 30(60) = 2600 $$
最適解は、これらの頂点の中で目的関数の値が最大となる点です。
上記よりこの例では、$$(0, 90)$$が最適解であり、$$ Z = 2700 $$となります。
シンプレックス法
続いて、シンプレックス法について簡単に説明します！
シンプレックス法は、線形計画法の中でも広く使用されていて、一言で表すと「許容解の空間を移動しながら最適解を探すアルゴリズム」となっています！
・初期の許容解を選定する。
・目的関数の値が改善する限り、隣接する許容解に移動していく。
・値の改善が見られなくなったら、その時点の解を最適解として終了。
１．初期解の設定：開始点を設定する。
２．方向の選択：どの方向に移動するかを決定する。
３．ステップサイズの決定：どのくらい移動するかを決定する。
４．解の更新：新しい解に移動し、この流れを繰り返す。
実際には少し複雑な計算等も発生しますがここでは割愛します。
簡単ですがシンプレックス法についても紹介しました！
メリットしては、非常に高い精度で最適解を求めることができ、かつ効率的に解を求めることができる点が挙げられます！
反対にデメリットとしては、初期解の選択が適切でないと計算が非効率になる可能性がある点や、高次元空間での計算量が膨大になることがある点が挙げられるでしょう。
線形計画法の応用例
線形計画法は多くの分野で広範に応用されており、限られた資源を最適に配分する問題を効率的に解決するための強力なツールです！
製造業から物流、金融、エネルギー、ヘルスケア、農業、マーケティング、公共政策、教育に至るまでさまざまな分野でその効果が発揮されています。
ここでは、その中のいくつかを取り上げて紹介します！
製造業
実際に本記事で取り上げた例は製造業に関するものでしたね！
生産計画では、複数の製品を生産するために限られた資源（労働力・機械・材料など）をどのように配分すれば最大の利益を得られるかを計画します！
また、製品の在庫管理においては、原材料の注文量や製品の生産量を最適化するために線形計画法が使用されます。
これにより、在庫コストを最小限に抑えつつ、需要に応じた供給を確保します。
物流・運輸
物流に関しては、複数の倉庫から複数の顧客に商品を配送する際に、輸送コストを最小化するルートを決定します！
また、配送業者が複数の車両を使って顧客に商品を届ける場合には、各車両のルートを最適化する必要があり、線形計画法を使って配送コストを最小化しつつ、時間内に配送を完了させるような最適なルートを見つけます。
マーケティング
マーケティング領域でも線形計画法は広く応用されています！
その一つが広告予算の配分。
企業が複数の広告チャネルに対して限られた予算をどのように配分すれば最も効果的かを決定する際に線形計画法を使用します。
最適な予算配分を見つけることで、広告効果を最大化します。
ヘルスケア
最後にへルスケア。
病院が限られた医療資源（医師、看護師、手術室、ベッド）を効率的に配分する際に線形計画法が使用されます。
最適なスケジュールを立てることで、患者の待ち時間を短縮し、医療サービスの質を向上させます。
Pythonでの線形計画法の実装
線形計画法の概要について掴んだところで、次はPythonでの実装例を見ていきましょう！
ここでは本記事で取り上げている製品の生産計画の問題を例に、Pythonで最適解を出力します！
以下の流れで進めていきます！
1. 目的関数の設定
2. 制約条件の設定
3. 線形計画法の実行と結果の表示
(4. 制約条件に用いる変数が3種類以上の問題にも適用可能！！)
1. 目的関数の設定
まずは必要なライブラリのインストールと、解きたい最適化問題の目的関数を設定します！
今回は以下を解きたいのでしたね！
$$最大化Z=40x+30y$$
こちらの係数をコード上で入力していくのですが、今回解きたい問題が最大化問題であるのに対し、多くのPythonのソルバーは最小化問題を解く仕様となっています。
よって「最大化問題を最小化問題に変換」する必要があります！
これを行うには目的関数の符号を反転させればよく、そのために係数が[-40, -30]とマイナスになっています！
from scipy.optimize import linprog
# 目的関数の係数（最小化問題として解くために、利益の負値を設定）
c = [-40, -30]2. 制約条件の設定
続いて、制約条件もステップ１と同様に係数を入力していきます！
入力したい制約条件は以下です！
$$2x+y\leq100（労働力の制約）$$
$$3x+2y\leq180（原材料の制約）$$
$$x\geq0,y\geq0（非負制約）$$
後ろ３行で非負制約を設定しています。
# 制約条件の係数
A = [[2, 1], [3, 2]]
b = [100, 180]
# 変数の非負制約を設定
x_bounds = (0, None)
bounds = [x_bounds, x_bounds]3. 線形計画法の実行と結果の表示
最後に、線形計画法を実行し、結果を表示させます！！
流れはとってもシンプルですね！
# 線形計画問題を解く
result = linprog(c, A_ub=A, b_ub=b, bounds=bounds, method='simplex')
# 結果の表示
print(f'Optimal value: {-result.fun}')
print(f'x_A (Product A): {result.x[0]}')
print(f'x_B (Product B): {result.x[1]}')
実際に表示された結果を確認してみましょう！
今回は製品Aを全く生産せず製品Bを90個生産するとしたときに利益が2700と最大になるという結果が読み取れます！
線形計画法の解法の章で説明した「図式解法」で求めた結果と一致していることがわかりますね！
4. 制約条件に用いる変数が3種類以上でも適用可能！
ステップ３までで、図式解法が可能な2変数での線形計画問題を例に出して実行してみました！
Pythonを利用すれば制約条件の変数が3つ以上に増えたパターンや、目的関数である変数（ここでは製品の種類）を3種類以上に増やしたパターンの問題も解くことが出来ます！
以下のコードでは、製品の種類が3種類に増え、制約条件に労働力と原材料だけでなく機械稼働時間という制約を加えています。
from scipy.optimize import linprog
# 目的関数の係数
c = [-50, -40, -30]
# 制約条件の係数
A = [
[1, 2, 1], # 労働力の制約
[2, 1, 3], # 原材料の制約
[1, 2, 2] # 機械稼働時間の制約
]
b = [100, 150, 120]
# 変数の非負制約を設定
x_bounds = (0, None)
bounds = [x_bounds, x_bounds, x_bounds]
# 線形計画問題を解く
result = linprog(c, A_ub=A, b_ub=b, bounds=bounds, method='simplex')
# 結果の表示
print(f'Optimal value: {-result.fun}')
print(f'x_A (Product A): {result.x[0]}')
print(f'x_B (Product B): {result.x[1]}')
print(f'x_C (Product C): {result.x[2]}')
コードとしては変数が増えても特段変わらないことがわかります！
結果は以下のように出力されました。
このように結果の個数が整数じゃないケースももちろんありますが、製品A：66個、製品B：16個、製品C：０個生産することが最大利益に近いことが読み取れます！
まとめ
本記事では、線形計画法の基本概念や具体例を用いた解法、Pythonでの実装方法まで詳しく解説しました！
線形計画法は、資源の最適配分やコストの最小化など、さまざまな場面でとても重要な役割を果たしています！
特に、複数の制約条件が存在する問題に対して、効率的な解を導くための強力なツールです。
また、Pythonを用いることで複雑な線形計画問題も簡単に解決することができることが分かりましたね！
ぜひ一度、ご自身のビジネスシナリオや研究テーマに合わせて、線形計画法を実装してみてください！
今回分析に用いたPythonについて勉強したい方は以下の記事を参考にしてみてください！
さらに詳しくAIやデータサイエンスの勉強がしたい！という方は当サイト「スタビジ」が提供するスタビジアカデミーというサービスで体系的に学ぶことが可能ですので是非参考にしてみてください！
AIデータサイエンス特化スクール「スタアカ」
| 【価格】 | ライトプラン：1280円/月 プレミアムプラン：149,800円 |
|---|---|
| 【オススメ度】 | |
| 【サポート体制】 | |
| 【受講形式】 | オンライン形式 |
| 【学習範囲】 | データサイエンスを網羅的に学ぶ 実践的なビジネスフレームワークを学ぶ SQLとPythonを組み合わせて実データを使った様々なワークを行う マーケティングの実行プラン策定 マーケティングとデータ分析の掛け合わせで集客マネタイズ |
データサイエンティストとしての自分の経験をふまえてエッセンスを詰め込んだのがこちらのスタビジアカデミー、略して「スタアカ」！！
当メディアが運営するスクールです。
24時間以内の質問対応と現役データサイエンティストによる複数回のメンタリングを実施します！
カリキュラム自体は、他のスクールと比較して圧倒的に良い自信があるのでぜひ受講してみてください！
他のスクールのカリキュラムはPythonでの機械学習実装だけに焦点が当たっているものが多く、実務に即した内容になっていないものが多いです。
そんな課題感に対して、実務で使うことの多いSQLや機械学習のビジネス導入プロセスの理解なども合わせて学べるボリューム満点のコースになっています！
Pythonが初めての人でも学べるようなカリキュラムしておりますので是非チェックしてみてください！
ウォルマートのデータを使って商品の予測分析をしたり、実務で使うことの多いGoogleプロダクトのBigQueryを使って投球分析をしたり、データサイエンティストに必要なビジネス・マーケティングの基礎を学んでマーケティングプランを作ってもらったり・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践してもらったりする盛りだくさんの内容になってます！
・BigQuery上でSQL、Google Colab上でPythonを使い野球の投球分析
・世界最大手小売企業のウォルマートの実データを用いた需要予測
・ビジネス・マーケティングの基礎を学んで実際の企業を題材にしたマーケティングプランの策定
・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践して稼ぐ
＼今すぐ試す／
# 線形計画問題を解く
result = linprog(c, A_ub=A, b_ub=b, bounds=bounds, method='simplex')
# 結果の表示
print(f'Optimal value: {-result.fun}')
print(f'x_A (Product A): {result.x[0]}')
print(f'x_B (Product B): {result.x[1]}')
スタビジのコンテンツをさらに深堀りしたコンテンツが動画と一緒に学べるスクールです。
プレミアムプランでは私がマンツーマンで伴走させていただきます！ご受講お待ちしております！
