強化学習を具体例と共にわかりやすく解説！Q学習をPythonで実装してみよう！

ウマたん

当サイト【スタビジ】の本記事では、強化学習について具体例と共に解説していきます！また最終的に強化学習の中で最も一般的なアルゴリズムであるQ学習をPythonで実装していきます。迷路の最適経路を見つけるプログラムを作っていきますよ！

データサイエンティストのウマたん(@statistics1012)です。

機械学習手法の中にある3つの学習手法の中でも特に今後多くの分野に応用されることが見込まれる「強化学習」

機械学習には教師あり学習・教師なし学習・強化学習の3つがあるのですが、教師あり学習・教師なし学習と比べてちょっと分かりにくく、とっつきにくいのが強化学習なんです。

この記事では、そんな強化学習について簡単にまとめていきたいと思います。

ウマたん

強化学習は今後様々なイノベーションを起こしていくだろう！

より詳しく強化学習について学びたい方は以下の私のUdemy講座で学べるのでぜひチェックしてみてください！

強化学習を学ぼう！Pythonで迷路問題やブラックジャックを強化学習させたエージェントを作っていこう！

【時間】	4時間
【レベル】	初級

強化学習についてガッツリ学びたいならこれ！Q学習のアルゴリズムを学び迷路最適ルート発見やブラックジャックの行動選択を強化学習で学習させていきます！

今なら購入時に「3X4948P6EZTY」という講師クーポンコードを入れると94%OFFになりますのでぜひご受講ください！

＼30日以内なら返金無料／このコースを見てみる

以下のYoutube動画でも解説しているのであわせてチェックしてみてください！

強化学習とは？

実は、強化学習自体のアルゴリズムは古くからあり有名な手法がQ学習という手法。

簡単に言うと、

ある状態sにおいてaという行動を取った場合の報酬をQ(s,a)と定義し、Q値の合計が最大になるような行動を取っていくというアルゴリズム

ロボたん

状態s?行動a?よくわからない、、、

ウマたん

大丈夫！みんなも人生で度々経験していることなんだ！

みなさんは自転車に乗ることはできるでしょうか？

今では不自由なく乗れる自転車も最初は何度か転んで試行錯誤しながら乗れるようになったはず。

この経験こそが強化学習そのものなのです。

強化学習のステップはシンプルです。

このループをまわすことで最も報酬を得やすい行動にチューニングしていくことができるのです。

正確には連続的な行動から得られる報酬の合計値である収益を最大化する行動をしていきます。

例えば自転車に乗るための行動は次のようなものです。

• ペダルをこぐ
• ハンドルを操作する（左右に曲がる）
• バランスを取る
• ブレーキをかける

子供はこれらの選択肢の中からその時の状態に応じてペダルをこいだり、ハンドルを操作してバランスを取ったりします。

各行動の結果として、うまく進めたり、転んだりします。うまく進めたときは「成功」の感覚を得て、転んだときは「痛い」や「怖い」と感じます。

子供は、特定の状態においてどの行動が良い結果（うまく進む）をもたらすかを記憶し行動を改善するのです！

このように強化学習は、自転車の乗り方を学ぶ子供が何度も試行錯誤を繰り返しながら、「どうやってうまく自転車に乗るか」を学ぶプロセスとよく似ています。

子供は転ぶこともありますが、転んだ経験を通じてどうすれば転ばないかを学びます。

これが強化学習の基本的な考え方です。

現実世界での行動と結果を通じて、徐々に最適な行動を選ぶようになるのです！

強化学習と機械学習とディープラーニングの関係性は？

ここで混乱しがちなのが、強化学習と機械学習とディープラーニングの違い。

強化学習＝ディープラーニング？と勘違いされていることもありますが、この2つは別物です。

あえて言うなら強化学習を取り入れたディープラーニングであるDeep Q-Network (DQN)というアプローチが有名なので強化学習=ディープラーニングという勘違いが起きてしまうのでしょう。

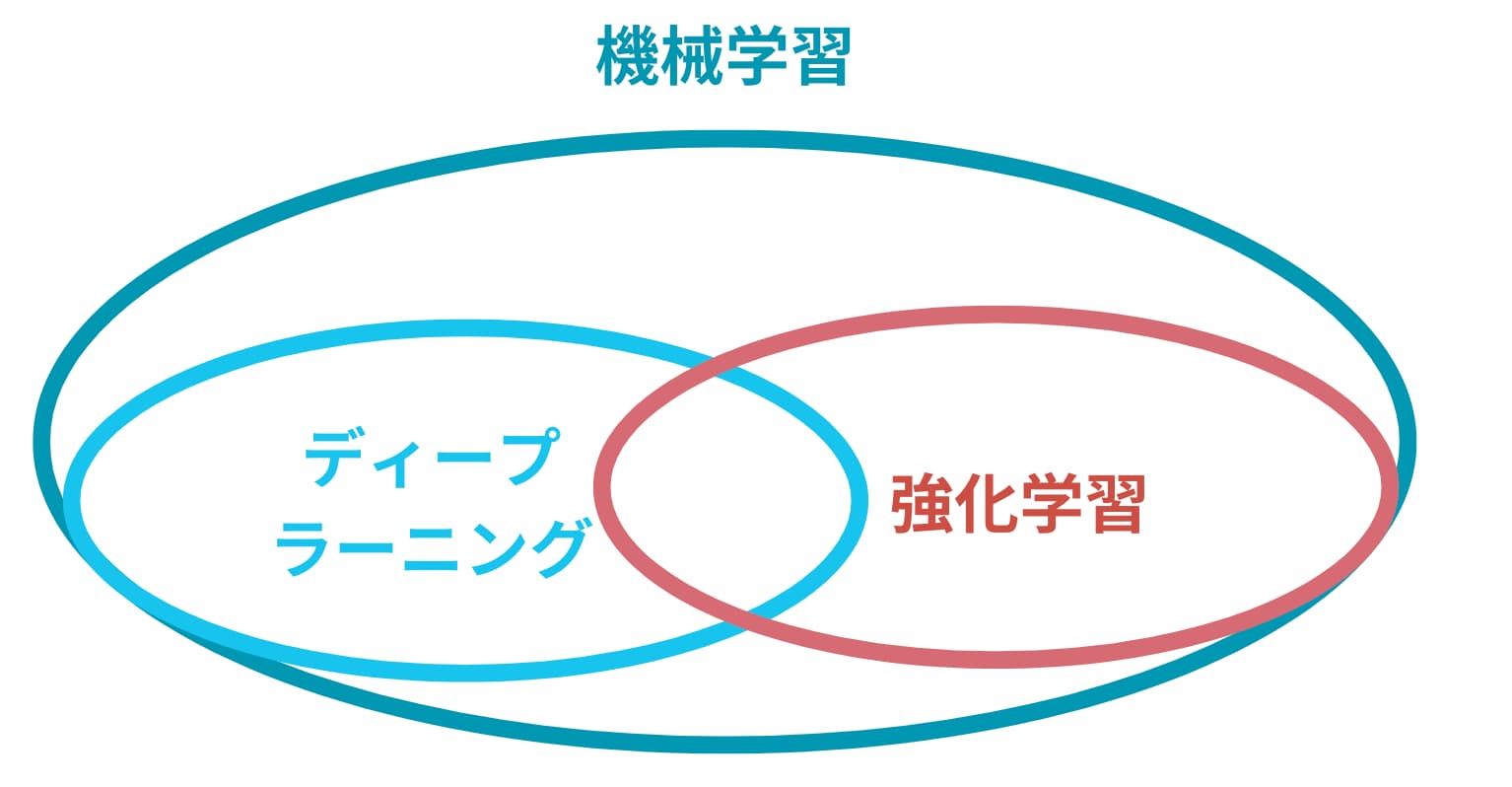
実際のところは、機械学習の一部に強化学習とディープラーニングが存在し、それらが重なることもあるけれど同一なものではないということです。

強化学習の具体例

それでは続いて強化学習の具体例について見ていきましょう！

自動運転

自動運転車の制御システムにも強化学習が利用されています。

車が安全に道路を走行するために、さまざまな状況に対する最適な行動を学習します。

例えば、他の車両との距離を保つ、信号や標識に従う、障害物を避けるなどのタスクを、実際の走行データやシミュレーションを通じて学びます。

自動運転技術は各社がこぞって開発にいそしんでいますが、やはりテスラが強いですねー！

既にテスラは世界中に展開して走っていてテスラ自体が走るソフトウェアでありリアルタイムで大量のデータを取得できるので他の会社と比べて圧倒的に強化学習のサイクルを回しやすいです。

格闘ゲームなどのCPU

強化学習は、ゲームのCPUの動きに適応されるなど既に様々な分野で実装されています。

例えば格闘ゲームなどは、その状態に応じて行動をして報酬を得ることの繰り返しになります。

強化学習を利用することで強いCPUを作ることができます。

AlphaGO

強化学習はそもそも学習に時間がかかるため行動パターンが複雑だと解を導くことができません。

囲碁は19×19もの数の交点があり、状態（s）と行動（a）のパターンが膨大です。

そこで登場したのがディープラーニング。

先ほどもお伝えしましたが、ディープラーニングと強化学習を組み合わせたDeep-Q-networkという手法をGoogleが開発し、それを基にプロ棋士をも凌駕する人工知能Alpha Goが作られたのです。

ちなみに囲碁は19×19であるのに対してチェスと将棋は9×9。将棋は取った将棋を新たに置くことができるのでチェスより複雑。

ということで、人工知能VS人類の勝負は、チェス（1997年）、将棋（2012年ごろ）、囲碁（2016年）に人類が敗北を喫しています。

強化学習をPythonで実装する方法

それでは最後に強化学習をPythonで実装してみましょう！

迷路の最適経路を進む問題を強化学習を使って考えていきます。

この時、強化学習の最適化アルゴリズムの中でも最も有名なQ学習を使っていきます。

それではコードを見ていきましょう！

いきなりコード全体を見ていきます。

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.colors as mcolors

# より複雑な迷路の設定
maze = np.array([
    [0, 1, 0, 0, 0, 1, 0, 0, 0, 0],
    [0, 1, 0, 1, 0, 1, 0, 1, 1, 0],
    [0, 0, 0, 1, 0, 0, 0, 0, 1, 0],
    [0, 1, 1, 1, 1, 1, 1, 0, 1, 0],
    [0, 1, 0, 0, 0, 0, 1, 0, 1, 0],
    [0, 1, 0, 1, 1, 0, 1, 0, 1, 0],
    [0, 0, 0, 0, 1, 0, 0, 0, 1, 0],
    [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 1, 1, 1, 1, 1, 1, 1, 1, 0]
])

# 定数の設定
START = (0, 0)
GOAL = (9, 9)
REWARD_GOAL = 100
REWARD_STEP = -1
ALPHA = 0.1
GAMMA = 0.9
EPSILON = 0.1
EPISODES = 200

# Qテーブルの初期化
q_table = np.zeros((maze.shape[0], maze.shape[1], 4))

# 行動の設定 (上、右、下、左)
actions = [(-1, 0), (0, 1), (1, 0), (0, -1)]

def is_valid(state):
    return 0 <= state[0] < maze.shape[0] and 0 <= state[1] < maze.shape[1] and maze[state] == 0

def next_state(state, action):
    next_state = (state[0] + action[0], state[1] + action[1])
    if is_valid(next_state):
        return next_state
    else:
        return state

def choose_action(state):
    if np.random.uniform(0, 1) < EPSILON:
        return np.random.choice(len(actions))
    else:
        return np.argmax(q_table[state])

def update_q_table(state, action, reward, next_state):
    best_next_action = np.argmax(q_table[next_state])
    td_target = reward + GAMMA * q_table[next_state][best_next_action]
    td_error = td_target - q_table[state][action]
    q_table[state][action] += ALPHA * td_error

# 学習
rewards = []
for episode in range(EPISODES):
    state = START
    total_reward = 0
    while state != GOAL:
        action = choose_action(state)
        next_st = next_state(state, actions[action])
        if next_st == GOAL:
            reward = REWARD_GOAL
        else:
            reward = REWARD_STEP
        update_q_table(state, action, reward, next_st)
        state = next_st
        total_reward += reward
    rewards.append(total_reward)

# 結果の可視化
plt.plot(range(EPISODES), rewards)
plt.xlabel('Episode')
plt.ylabel('Total Reward')
plt.title('Total Rewards per Episode')
plt.show()

# 学習結果の確認と迷路の可視化
state = START
path = [state]
while state != GOAL:
    action = np.argmax(q_table[state])
    state = next_state(state, actions[action])
    path.append(state)

# 迷路と経路の可視化
maze_with_path = maze.copy()
for s in path:
    maze_with_path[s] = 2

cmap = mcolors.ListedColormap(['white', 'black', 'red'])
bounds = [0, 0.5, 1.5, 2.5]
norm = mcolors.BoundaryNorm(bounds, cmap.N)

plt.figure(figsize=(10, 10))
plt.imshow(maze_with_path, cmap=cmap, norm=norm)
plt.title('Maze and Optimal Path')
plt.show()

print("Optimal Path:")
print(path)

結果は以下のようになりました。

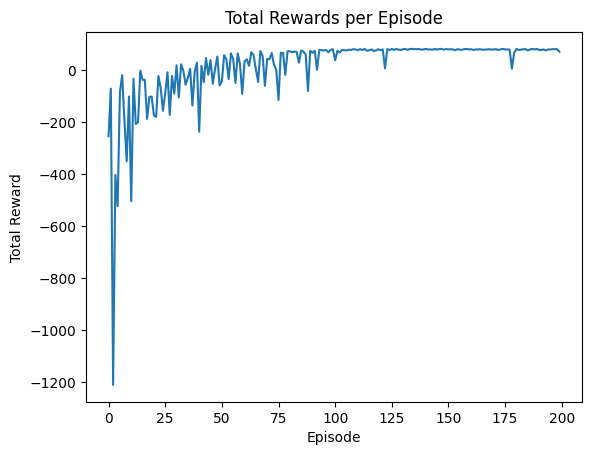
こちらはTotal Rewardを縦軸に回数を横軸に取ったグラフを表しています。

最初の方はTotal Rewardが大きくマイナスなのですが徐々に上昇していき100回を超えたあたりからほぼ高止まりしていることが分かります。

最終的に見つけ出した迷路の最適経路は以下の通りです。

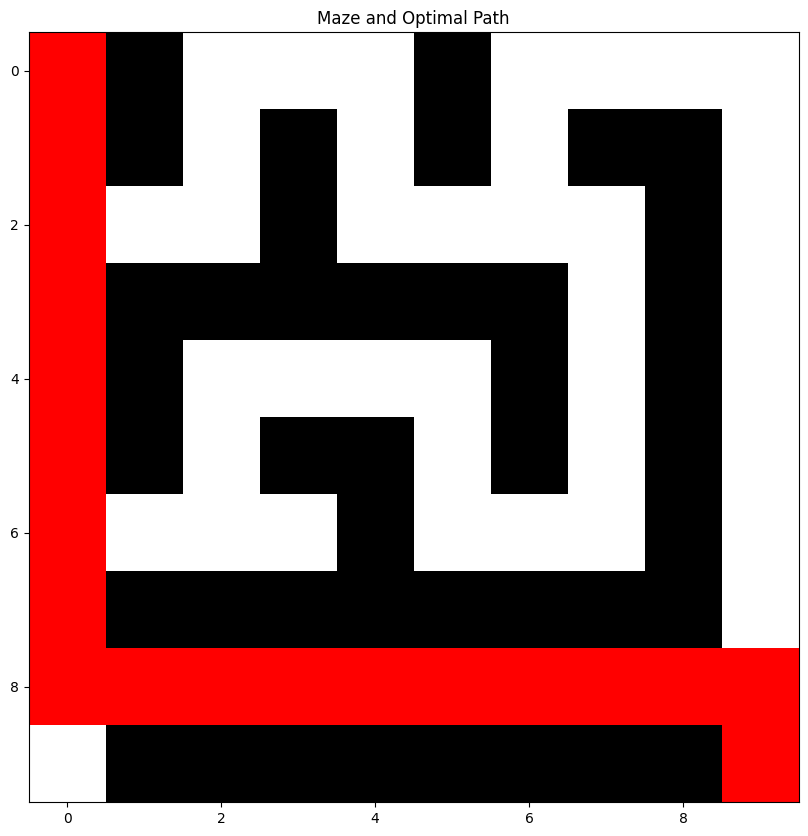
まさに無駄な道を通らず最適にゴールにたどり着いていることが分かりますね！

このように強化学習を使えば試行錯誤を繰り返しながら最適な経路を見つけ出すことができるのです。

それではコードの中身を具体的に見ていきましょう！

各種事前設定

まずは各種設定を進めていきます。

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.colors as mcolors

# より複雑な迷路の設定
maze = np.array([
    [0, 1, 0, 0, 0, 1, 0, 0, 0, 0],
    [0, 1, 0, 1, 0, 1, 0, 1, 1, 0],
    [0, 0, 0, 1, 0, 0, 0, 0, 1, 0],
    [0, 1, 1, 1, 1, 1, 1, 0, 1, 0],
    [0, 1, 0, 0, 0, 0, 1, 0, 1, 0],
    [0, 1, 0, 1, 1, 0, 1, 0, 1, 0],
    [0, 0, 0, 0, 1, 0, 0, 0, 1, 0],
    [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 1, 1, 1, 1, 1, 1, 1, 1, 0]
])

# 定数の設定
START = (0, 0)
GOAL = (9, 9)
REWARD_GOAL = 100
REWARD_STEP = -1
ALPHA = 0.1
GAMMA = 0.9
EPSILON = 0.1
EPISODES = 200

# Qテーブルの初期化
q_table = np.zeros((maze.shape[0], maze.shape[1], 4))

# 行動の設定 (上、右、下、左)
actions = [(-1, 0), (0, 1), (1, 0), (0, -1)]

まず、迷路を10×10のマスで表していて、通れる道を0、壁を1で表現しています。

続いてスタートの初期値とゴールの位置を定義しています。

報酬の定義

さらにREWARD_GOAL = 100ではゴールした際に得られる報酬、REWARD_STEP = -1では行動の度に減る報酬を定義しています。

すなわちこの問題では、どこかに移動する度に1点報酬が減り、最終的にゴールした際に100点もらえるようになっています。

すなわち報酬の合計を最大化するためには最短の移動でゴールすることが求められます。

学習率の定義

続いてALPHA = 0.1では学習率を定義しています。

学習率は、新しい行動をした時にその行動を元にどのくらいQ値（最適な行動を選ぶためのテーブル）を更新するかの更新率を表します。

割引率の定義

またGAMMA = 0.9では割引率を定義しています。

割引率は将来の報酬を現在価値に置き換えた時にどのくらい割り引いて考えるかの指標です。

今回のケースではそれほどあまり意味がないかもしれませんが、全体の報酬を考える上でなるべく将来よりも現在の報酬に重きを置いた方がよいケースがあります。

探索率の定義

EPSILON = 0.1では探索率を定義しています。

Q学習では現在の状態に応じて最適な行動を取るようなアプローチを取っていきますが、常に現在のQ値に応じて最適な行動を取っていては新たな可能性を模索できません。

そこで探索率を設けて、一定の確率でランダムな行動を行うようにします。

施行回数・Qテーブル・行動の定義

続いて、EPISODES = 200では施行回数を定義しています。今回はゴールに至るまでの施行を200回繰り返します。

続いてQテーブルを定義しています。これは現在の状態（10×10のどこにいるか）に対しておこなった行動（上、右、下、左）に応じてもらえるQ値（もらえる報酬）を表します。

これにより現在の状態において最適な行動を取れるようになります。

各種関数の定義

続いて関数の定義をしています。

def is_valid(state):
    return 0 <= state[0] < maze.shape[0] and 0 <= state[1] < maze.shape[1] and maze[state] == 0

def next_state(state, action):
    next_state = (state[0] + action[0], state[1] + action[1])
    if is_valid(next_state):
        return next_state
    else:
        return state

def choose_action(state):
    if np.random.uniform(0, 1) < EPSILON:
        return np.random.choice(len(actions))
    else:
        return np.argmax(q_table[state])

def update_q_table(state, action, reward, next_state):
    best_next_action = np.argmax(q_table[next_state])
    td_target = reward + GAMMA * q_table[next_state][best_next_action]
    td_error = td_target - q_table[state][action]
    q_table[state][action] += ALPHA * td_error

まずis_valid関数では、次に選んだ状態が迷路の中にあるか、そして壁ではないかを判定しています。

そしてnext_state関数では、現在の状態からの次の状態を定義しそこにis_valid関数を適用させて問題なければ次の状態に移動、問題があれば元の状態のままにします。

choose_action関数では、探索率の確率でランダムに行動を決めて、それ以外はQテーブルに基づいて現時点での最適な行動をとります。

そして最後にupdate_q_tableでは、Qテーブルの値を更新しています。

学習と可視化

そして事前設定と関数の定義が完了したので実際に学習と結果の可視化を進めていきます。

# 学習
rewards = []
for episode in range(EPISODES):
    state = START
    total_reward = 0
    while state != GOAL:
        action = choose_action(state)
        next_st = next_state(state, actions[action])
        if next_st == GOAL:
            reward = REWARD_GOAL
        else:
            reward = REWARD_STEP
        update_q_table(state, action, reward, next_st)
        state = next_st
        total_reward += reward
    rewards.append(total_reward)

# 結果の可視化
plt.plot(range(EPISODES), rewards)
plt.xlabel('Episode')
plt.ylabel('Total Reward')
plt.title('Total Rewards per Episode')
plt.show()

# 学習結果の確認と迷路の可視化
state = START
path = [state]
while state != GOAL:
    action = np.argmax(q_table[state])
    state = next_state(state, actions[action])
    path.append(state)

# 迷路と経路の可視化
maze_with_path = maze.copy()
for s in path:
    maze_with_path[s] = 2

cmap = mcolors.ListedColormap(['white', 'black', 'red'])
bounds = [0, 0.5, 1.5, 2.5]
norm = mcolors.BoundaryNorm(bounds, cmap.N)

plt.figure(figsize=(10, 10))
plt.imshow(maze_with_path, cmap=cmap, norm=norm)
plt.title('Maze and Optimal Path')
plt.show()

print("Optimal Path:")
print(path)

今までの説明からなんとなく分かると思いますが、Qテーブルの情報から現在の状態にあわせて最適な行動を取りそれに基づいてQテーブルの情報を更新していきます。

それをゴールにたどり着くまで繰り返すという処理を200回繰り返していきます。

一見複雑そうに見えますが、思ったよりも複雑ではないことが分かると思います！

なんとなく強化学習のQ学習のアプローチについて理解いただけたでしょうか？

ぜひおさえておいてください！

強化学習　まとめ

ここまで読んでいただきありがとうございました！

本記事では、強化学習に関して解説してきました。

強化学習は今後のAI時代において非常に重要なアプローチです。

ここでは概論だけお伝えしてきましたが、もっと深く知りたい方は以下のYoutubeの強化学習シリーズを参考にしてみてください！

これだけ詳しくわかりやすく強化学習について解説しているYoutubeは見たことがありません。

さらに、より詳しく強化学習について学びたい方は以下の私のUdemy講座で学べるのでぜひチェックしてみてください！

強化学習を学ぼう！Pythonで迷路問題やブラックジャックを強化学習させたエージェントを作っていこう！

【時間】	4時間
【レベル】	初級

強化学習についてガッツリ学びたいならこれ！Q学習のアルゴリズムを学び迷路最適ルート発見やブラックジャックの行動選択を強化学習で学習させていきます！

＼30日以内なら返金無料／このコースを見てみる

また、さらに詳しくAIやデータサイエンスの勉強がしたい！という方は当サイト「スタビジ」が提供するスタビジアカデミーというサービスで体系的に学ぶことが可能ですので是非参考にしてみてください！

AIデータサイエンス特化スクール「スタアカ」

【価格】	ライトプラン：1280円/月 プレミアムプラン：149,800円
【オススメ度】
【サポート体制】
【受講形式】	オンライン形式
【学習範囲】	データサイエンスを網羅的に学ぶ 実践的なビジネスフレームワークを学ぶ SQLとPythonを組み合わせて実データを使った様々なワークを行う マーケティングの実行プラン策定 マーケティングとデータ分析の掛け合わせで集客マネタイズ

データサイエンティストとしての自分の経験をふまえてエッセンスを詰め込んだのがこちらのスタビジアカデミー、略して「スタアカ」！！

当メディアが運営するスクールです。

24時間以内の質問対応と現役データサイエンティストによる複数回のメンタリングを実施します！

カリキュラム自体は、他のスクールと比較して圧倒的に良い自信があるのでぜひ受講してみてください！

他のスクールのカリキュラムはPythonでの機械学習実装だけに焦点が当たっているものが多く、実務に即した内容になっていないものが多いです。

そんな課題感に対して、実務で使うことの多いSQLや機械学習のビジネス導入プロセスの理解なども合わせて学べるボリューム満点のコースになっています！

Pythonが初めての人でも学べるようなカリキュラムしておりますので是非チェックしてみてください！

ウォルマートのデータを使って商品の予測分析をしたり、実務で使うことの多いGoogleプロダクトのBigQueryを使って投球分析をしたり、データサイエンティストに必要なビジネス・マーケティングの基礎を学んでマーケティングプランを作ってもらったり・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践してもらったりする盛りだくさんの内容になってます！

・BigQuery上でSQL、Google Colab上でPythonを使い野球の投球分析
・世界最大手小売企業のウォルマートの実データを用いた需要予測
・ビジネス・マーケティングの基礎を学んで実際の企業を題材にしたマーケティングプランの策定
・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践して稼ぐ

＼今すぐ試す／スタアカの受講はこちら