こんにちは!データサイエンティスト兼デジタルマーケターのウマたん(@statistics1012)です
過去のデータを元に将来のデータを予測したい!
こういう場面って多いですよね?
店舗の売り上げに関してもそうだし、株価だってそうだし視聴率だって。
そんな時に登場するのが時系列分析!
そんなやっかいな時系列データですが、なかなか分かりやすい書籍がない!
沖本さんの「計量時系列分析」は、確かに良書ですがとっかかりとしては難易度が高いんです。
(2025/12/14 22:27:45時点 Amazon調べ-詳細)
こちらの「現場で使える時系列データ分析」は簡単な説明とRによる実装が分かりやすく書いてありますが、理論的な内容は薄いです。
(2025/12/14 17:18:33時点 Amazon調べ-詳細)
個人的には「現場で使える時系列データ分析」を読んだ後に「計量時系列分析」を読めばよいかなと思ってます。
ちなみに以下の記事でおすすめの時系列分析の本をご紹介しているのでよかったら見てみてください。

そんなこんなでなかなか難しい!という声を聞く時系列分析についてこの記事でまとめておきます!
Rでの実装や深い理論が気になる方は前述した2冊を読んでみてください!
目次
そもそも時系列分析とは?
当たり前ですが、得られたデータに順序があるデータを時系列データと呼びます。
逆にデータに順序がなく一つの時期に複数のデータがある状況をクロスセクションデータと呼びます。
また、結構実データ解析とか行っていると遭遇する可能性の高いデータにパネルデータと呼ばれるものがあります。
これは、時系列データとクロスセクションデータが組み合わさったもの!
簡単な具体例を挙げると、
特定の店舗の10年間の売り上げは時系列データ
全国チェーンの各店舗の1日の売り上げはクロスセクションデータ
全国チェーンの各店舗の10年間の売り上げデータはパネルデータ
となります。
パネルデータを用いることの利点は第一に,これまでのクロスセクション ・データや時系列デー夕と比べた場合,観察点が格段に増加するので推定精度が上がることが期待できる
(引用元:Google-「パネルデータの意義 とその活用」)
パネルデータの解析はまた違ったアプローチがあるので置いておいて、今回は一つの店舗での売り上げデータである時系列データのお話をしましょう!
時系列データ分析をする上でおさえておきたい基礎知識
まずはじめに時系列データ分析をする上でおさえておきたい基礎知識についてまとめておきましょう!
クロスセクションデータにはない自己共分散
クロスセクションデータいわゆる静的なデータに良く用いられる統計量として平均・分散・標準偏差・共分散・相関係数などがありますね。
その中で相関を求める上で重要になってくる共分散。
共分散を求めることで各変数の相関構造を求めたりデータの構造を知ることができるのですが、時系列データには自己共分散という概念が存在します。
各期の観測値\(y_t\)、各期の期待値を\(\mu_t\)とした時、自己共分散の定義はこんな感じ!(参考:計量時系列分析)
\begin{eqnarray}
Cov(y_t,y_{t-1})=E[(y_t-\mu_t)(y_{t-1}-\mu_{t-1})]
\end{eqnarray}
各期の共分散というイメージですね。
すなわち共分散が正の場合その期同士は平均に対して同じ方向への挙動を示しやすく、負の場合は平均に対して違う方向への挙動を示しやすいということです。
・共分散が正の場合、同じ方向への挙動
・共分散が負の場合、違う方向への挙動
この自己共分散は自己相関につながり、時系列データの構造を把握する上で非常に重要になってきます。
定常性という概念
まず、時系列分析において確認しておかなくてはならないのが定常性の概念!
定常性には弱定常性と強定常性があるんですが、正直確認しておくのは弱定常性だけで良いでしょう!
基本的にこの弱定常性が仮定されないと統計的な解釈はできません。
弱定常性の定義はこちら!(参考:計量時系列分析)
任意の\(t\)と\(k\)において
\begin{eqnarray}
\left\{
\begin{array}{l}
E(y_t)&=&\mu\\
Cov(y_t,y_{t-k})&=&E[(y_t-\mu)(y_{t-k}-\mu)]\\
\end{array}
\right.
\end{eqnarray}
数式で見てもいきなりは分からないと思うんですが、
期ごとの期待値(平均値)は一緒だよということと
期の差が同じなら共分散は一緒だよということ
です。
・期ごとの期待値(平均値)は一緒
・期の差が同じなら共分散は一緒
これらを満たしているのならそのデータは弱定常となります。
具体的にどのような状況かというと、各期の平均が一緒なので上昇傾向はないよということ。
長期的に見ても平均は動かず一緒です。
そして、期の差が同じなら共分散は一緒というのは、平均へ回帰してくるイメージ。
2期先の共分散が負なら常に2期の周期で平均へ戻ってきますよね。今期が正の方向なら2期先の期は負の方向に移動するので。
この二つの制約条件を守ってくれるのが弱定常というわけです!
なんだかばらつきながらジクザグしているけど全体で見たら平坦なデータって感じ。
一番単純なのはこんな感じのやつ。
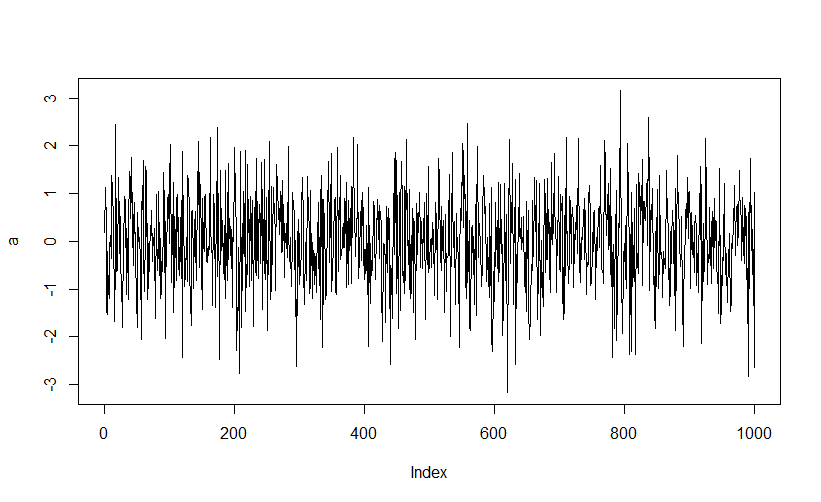
Rで簡単に記述できます。
弱定常性のことをただ単に定常と呼ぶこともあるのでここでも弱定常のことを定常と呼ぶことにします。
ちなみにこの定常性を満たさないものを非定常と呼びます。
店舗の売り上げデータも株価データも視聴率データもぜーんぶ基本的には非定常です。
このあとに出てくるMAモデルもARモデルも定常性を仮定して当てはめるのでこの定常性という概念は必ず覚えておきましょう!
強定常性という概念もあるんですが、弱定常性のことを単に定常と呼ぶこともあるくらい、そこまで解析においては重要でない概念なのでここでは弱定常性だけにとどめておきます。
強定常性に関しては沖本さんの本を読んでみてください!
定常性について詳しくはこちらでまとめています。

時系列データ分析のモデル
続いて時系列データ分析に用いられるモデルについて簡単に見ていきましょう!
MAモデル
やっと時系列モデリングのお話に入ります。
時系列データのほとんどは、前述した自己共分散すなわち自己相関を持っています。
自己相関を持ったデータをモデリングする方法としてはどのようなものが考えられるでしょうか?
たとえば
\begin{eqnarray}
\left\{
\begin{array}{l}
y_t&=&a+b\\
y_{t-1}&=&b+c\\
\end{array}
\right.
\end{eqnarray}
こんな感じ。
このようにモデリングすると、共通の成分\(b\)を通して、\(y_t\)と\(y_{t-1}\)が相関をもつことが期待できますね!
これがMA(Moving Average)モデルの考え方です。
MAモデルとはホワイトノイズと呼ばれる誤差項を共通項にすることで各期が相関を持ったモデルです。
\begin{eqnarray}
y_t=\mu+\epsilon_t+\theta_1\epsilon_{t-1} ,
\epsilon_t\sim{W.N.(\sigma^2)}
\end{eqnarray}
※ホワイトノイズは全ての期において平均\(0\)分散\(\sigma^2\)を満たし、\(W.N.(\sigma^2)\)と記述する。
こんな感じ。
ホワイトノイズを元に\(y_t\)と\(y_{t-1}\)が相関を持っているのが分かります!
また、\(\theta_1\)というパラメータが\(y_t\)と\(y_{t-1}\)の相関の強さを決めているのが分かりますね。
これは\(y_t\)と\(y_{t-1}\)の相関しか記述していないので1次自己相関と呼びますが、2次、3次・・・といくらでも記述することは可能です。
最適なあてはまりの良い次数を決定してモデリングするんです→ここらへんは重回帰におけるモデリング決定理論と同じでAICを用いたりします。
詳細は省きますが、このMAモデルは常に定常になります。
ARモデル
またもう一つは、
\(y_t=ay_{t-1}+b\)
こんな感じにして\(y_t\)を\(y_{t-1}\)で表せるようにしたモデル。これが相関を持つのは明らかですね!
これがAR(autoregressive process)モデルの考え方です。
1次のARモデルは、
\begin{eqnarray}
y_t=c+\phi_1{y_{t-1}}+\epsilon_t,
\epsilon_t\sim{W.N.(\sigma^2)}
\end{eqnarray}
と定義されます。
\(\phi_1\)を元に\(y_t\)と\(y_{t-1}\)が相関を持っているのが分かりますね!
この時、\(|\phi_1|>1\)となってしまったらどうなるでしょうか。
そう、発散してしまうんですね。すなわち非定常です。
そのため基本的にARモデルにおける\(\phi_1\)は\(|\phi_1|<1\)で与えます。
ARMAモデル
そして、これらのMAモデルとARモデルをどちらもモデルに組み込んだのが、
ARMAモデル!
ARMAモデルを記述するとこんな感じ!
\begin{eqnarray}
y_t=c+\phi_1{y_{t-1}}+\epsilon_t+\theta_1\epsilon_{t-1}, \epsilon_t\sim{W.N.(\sigma^2)}
\end{eqnarray}
単純にARモデルとMAモデルのモデル式を組み合わせただけですね!
これはARモデルもMAモデルも1次相関しか持たせていませんが、2次、3次・・・と項を増やすことでより柔軟なモデリングが可能になります!
多くの時系列データに対してこのARMAモデルに当てはめて構造把握や予測を行うことになります!
ARIMAモデル
ARMAモデルを少し拡張したのがARIMAモデル!
基本的に株価や視聴率や売り上げなどのトレンドや季節要因のある非定常データは、そのままARMAモデルを当てはめても上手くいかないことが多いです。
しかし、それらのデータは期ごとの差分をとることで定常性が満たされることが多いです。
その時系列データの差分をとって差分のデータに落とし込むことで定常にし、ARMAモデルを適用しよう!とするのがARIMAモデルです!
ディープラーニングによる時系列データ分析(RNN)
最先端の技術であり日々進化を続けるディープラーニング。
そんなディープラーニングにはRNN(リカレントニューラルネットワーク)という手法が存在します。
これにより、時系列データをディープラーニングにより分析できるようになったのです。
通常のディープラーニングは情報が別のレイヤーに伝播していきますが、
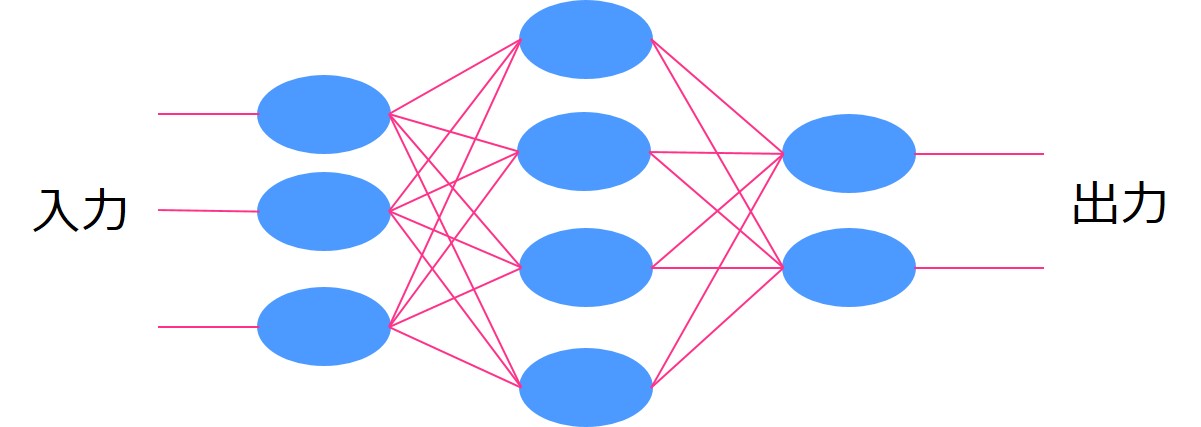
リカレントニューラルネットワークでは同じレイヤーに情報が伝播していきます。
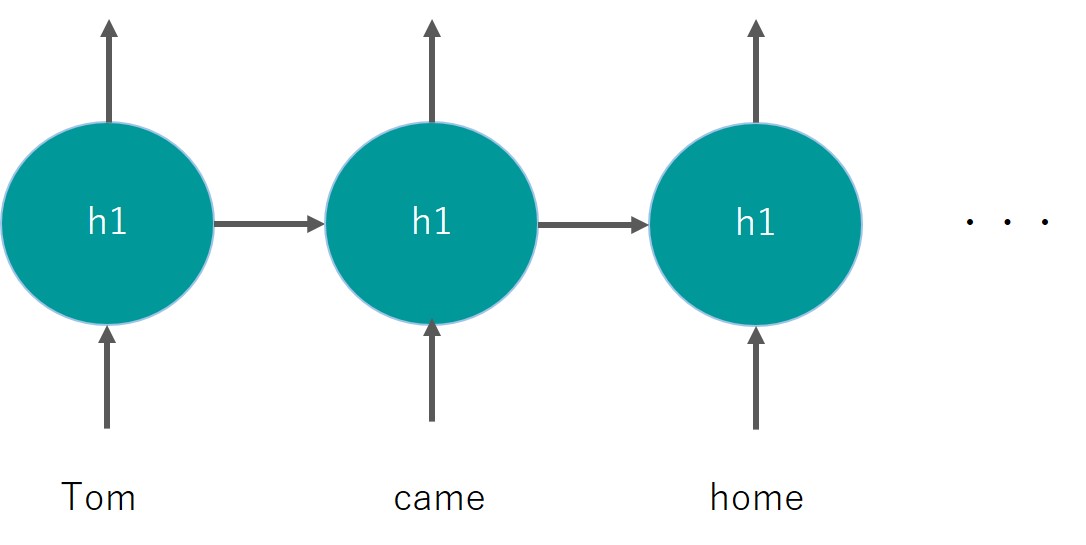
時系列データ分析というと株価や売り上げデータなどをイメージされると思いますが、実は言語処理も文字の時系列データになるのです。
Google翻訳やAIスピーカーなどの技術もRNNを基にしているんですよー!!
詳しく知りたい方は、以下の書籍を見てみてください!
また記事でもまとめていますのでよければのぞいてみてください!

時系列データ分析 まとめ
本記事では、時系列データにおける定常性の概念からモデリングの理論的な話をしてきました。
時系列データ分析について学ぶにためにはもはや王道になっている以下の沖本さんの書籍は購入しておいて損はないでしょう!
(2025/12/14 22:27:45時点 Amazon調べ-詳細)
さらに時系列データ分析についてもっと知りたいという方はこちらでオススメの本をまとめていますので是非ご覧ください!

データサイエンスや機械学習の勉強方法については以下の記事で詳しくまとめているのでチェックしてみてください!