機械学習と統計学/多変量解析の違いについてデータサイエンティストがモノ申す!!

こんにちは!
データサイエンティストのウマたん(@statistics1012)です!
大学院時代は統計学専攻で、伝統的な統計学から割と最近の機械学習まで扱っていました。
みなさんは、機械学習と聞くとどんなイメージを持ちますか?
割と最近の手法というイメージを持つのではないでしょうか?
それでは、重回帰分析は機械学習手法でしょうか?
機械学習という言葉は便利なので様々なところで使われており、言葉が独り歩きしている感もあります。
機械学習使っとけばいいんだ!的な風潮は危ないですね。
「スタビジ」でも機械学習手法と統計学は明確に分けております。
統計学に端を発する手法群は多変量解析と呼ばれることが多いです。
そんなイマイチ境目の分からない機械学習と統計学(多変量解析)の違いについて見ていきましょう!
Youtubeでも解説していますのでよければチェックしてみてくださいね!
目次
機械学習と統計学の違い

機械学習と統計学の大きな違いは、目的の違いにあります。
・機械学習手法は精度追求型
・統計学的手法は解釈追求型
どういうことか見ていきましょう。
機械学習手法は精度追求型
機械学習手法は徹底的に精度を追い求めます。
高いパフォーマンスを出せば出すほど良いのです。
そのため、アルゴリズムが複雑で中身がブラックボックスであったとしても問題ありません。
精度が少しでも上がれば良いのです。
逆に予測精度を追求することで、データの構造は可視化しにくくなっています。
そのため、出てきた結果に対して解釈の余地を与えられないことが多いです。
機械学習手法では、データの型を特に気にしませんのでどんな構造のデータでもとにかくアルゴリズムに突っ込むとそれなりの結果が出てきます(各種パラメータチューニングをする必要はあります)
統計学的手法は解釈追求型

一方で、統計学的アプローチは現状のデータの構造を可視化し、解釈を与えることに意味を見出します。
そのため、なるべくアルゴリズムは単純かつ分かりやすいモノを好みます。
また統計学的手法では、データの型をあらかじめ想定してモデルを組みます(パラメトリックモデル)。
そのためデータが想定したモデルにぴったり合致した時の威力はすさまじいモノがあります。
実際にビジネスに活かすことが出来るのは解釈追求型の統計学的手法であることも多いです。
ただ、得られた結果から相関関係は分かりますが因果関係がほぼ分からないということを念頭に置いておくことが大事です。
ほとんどの場合、因果関係は分かりません。
因果関係を苦労して探して紐解いた頃には因果は変わってしまっているかもしれないのです。
基本的には、相関関係から導き出したビジネスソリューションに対して成功したら、やはり因果関係があったんだねと証明できることになります。
統計学の学問の中には統計的因果推論という奥深い分野もあります。

機械学習手法と統計学的手法の使い分けの違い

それではどんな時に機械学習手法を用いて、どんな時に統計学的手法を用いると良いのでしょうか?
機械学習手法を用いる場面
先ほども述べましたが機械学習は精度追求型です。
そのため、データの構造はよく分からないけどとりあえず予測精度が高くなれば良い!という場面で好まれます。
例えば、ユーザーレコメンドや広告配信アロケーションなどロジックは分からなくても精度さえ高くなれば良いという場面で用いられます。
統計学(多変量解析)を用いる場面
データの構造を紐解いてそこから新たな知見を導き出したい場合、統計学的アプローチが用いられることが多いです。
また他人に提案・報告する上でも説明しやすいので、上位レイヤーへの提案やコンサルから事業会社への提案は、統計学的アプローチを使っていることが多いです。
また機械学習に比べるとアルゴリズムが単純で計算スピードも速いので、それほど精度を追求する意味がない場合は統計学的アプローチを用いたほうが良いです。
機械学習手法と統計学的手法の種類
それでは最後に機械学習手法にはどのような手法があるのか、統計学的手法にはどのような手法があるのか見ていきたいと思います。
正直、境目が微妙な手法もありますのでご了承ください。
機械学習手法
機械学習手法の種類は数え上げたらキリがありませんので、ここでは有名どころを挙げておきます。
ランダムフォレスト
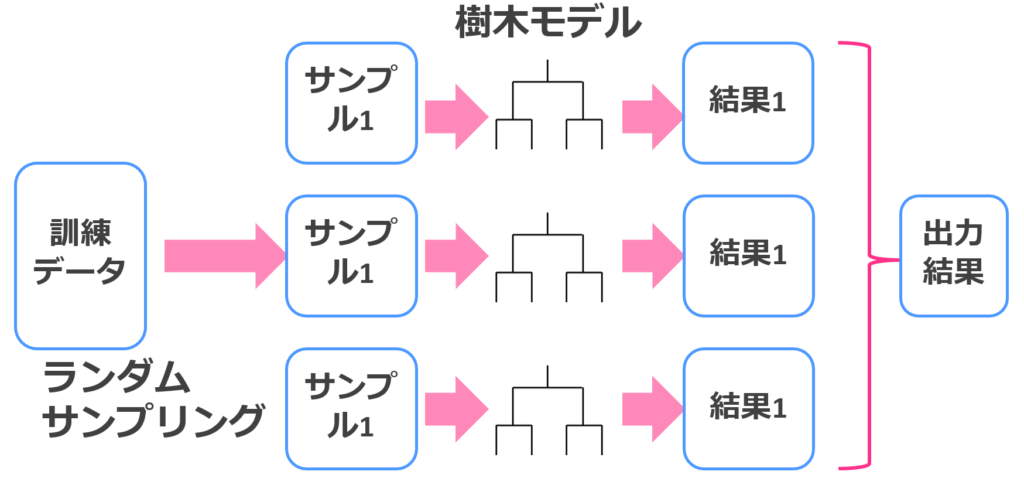
ランダムフォレストは、決定木とバギングを組み合わせた手法でそれなりの精度を簡単にたたき出してくれます。
それほど計算負荷もかからないので、ちょっとしたデータを解析するのにはもってこいです。
ランダムフォレストに関してはこちらの記事を参考にしてみてください。

SVM(サポートベクターマシン)
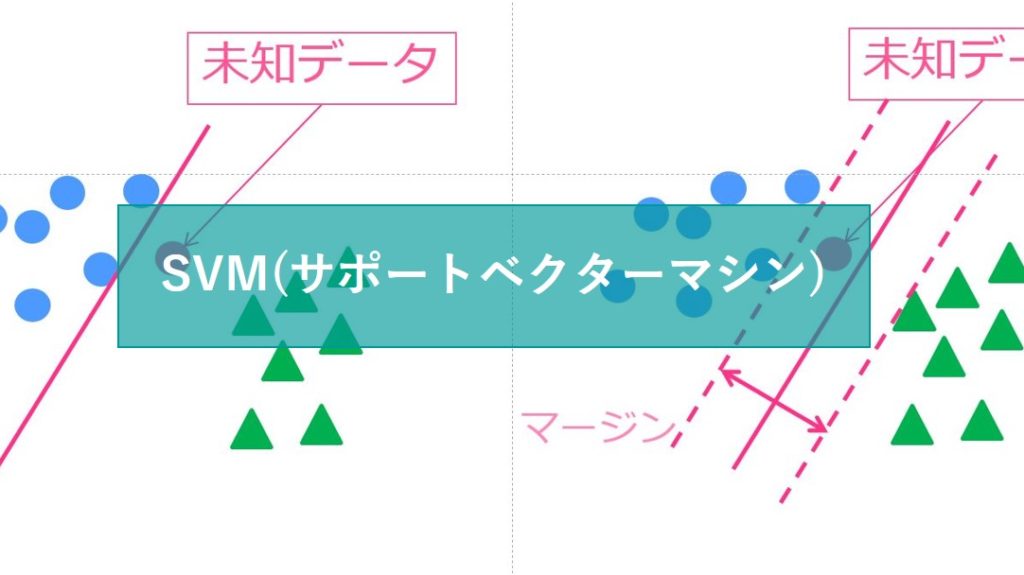
SVMもランダムフォレスト同様の精度が期待できる優秀な手法です。
応用の幅が広く様々な分野で使われています。計算負荷は高めです。
SVMについて詳しくはこちら!

ニューラルネットワーク
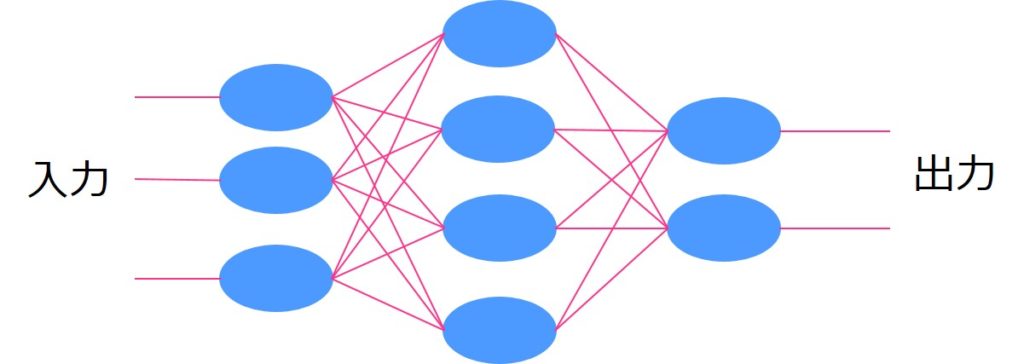
ニューラルネットワークはディープラーニングの基となった手法です。
ニューラルネットワーク単体ではそれほど高い精度は見込めませんが、中間層を増やせば増やすほど学習が進み(ディープラーニングに近づき)精度が高くなります。
その分、計算負荷も上昇します。
ニューラルネットワークに関して詳しくはこちら!

XGboost
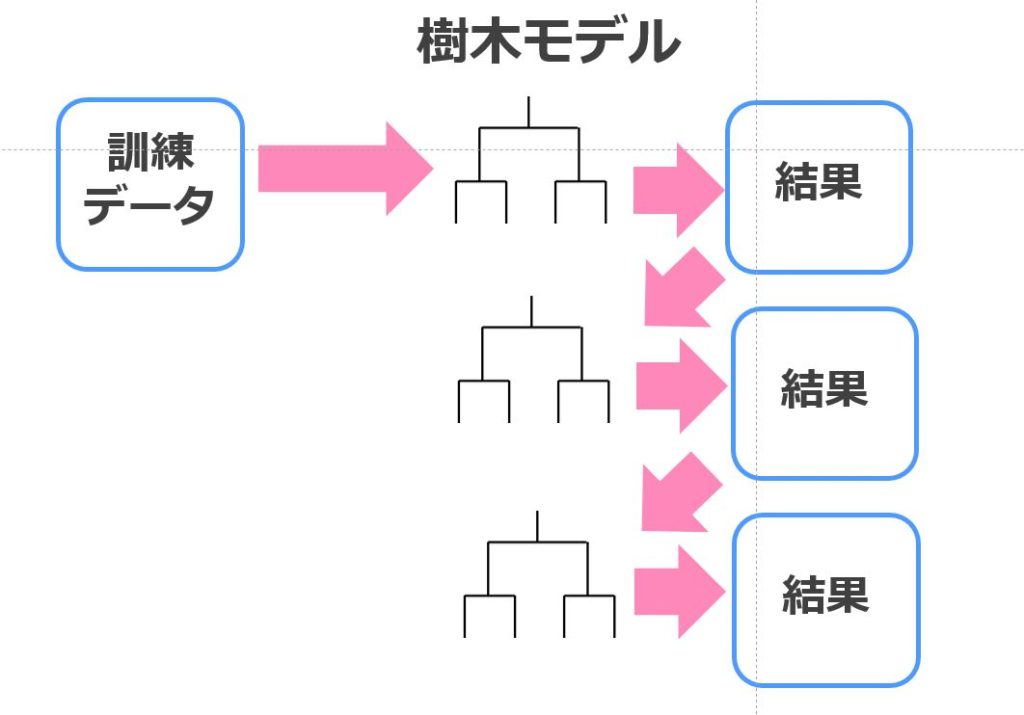
XGboostは、決定木と勾配ブースティングを組み合わせた手法で相当高い精度が見込めます。
教師あり学習の中では、今でも十分最前線で使われている優秀な手法になっております。
XGboostに関しては以下の記事をご覧ください!

勾配ブースティング手法は他にもいくつかあります。
Xgboostの後発であるLightGBM、Catboostなんてのもあり、高精度が見込めますので興味のある方はチェックしてみてください!

統計学的手法
統計学的手法もいくつか種類がありますので、ここでは押さえておきたい手法群だけピックアップしておきます。
重回帰分析(線形回帰)
重回帰分析は最も一般的であり、アルゴリズムも分かりやすい手法。
回帰系手法の中で最も分かりやすく、結果の解釈も容易。
実装が容易で、実務の場でも良く用いられている手法の1つです。
回帰分析に関してはこちらの記事にまとめています。

主成分分析
主成分分析は次元圧縮の場面で使われます。
主成分分析を用いることで、複数ある変数をいくつかの変数で表現することができます。
主成分分析に関しては以下の記事にまとめています!

クラスター分析
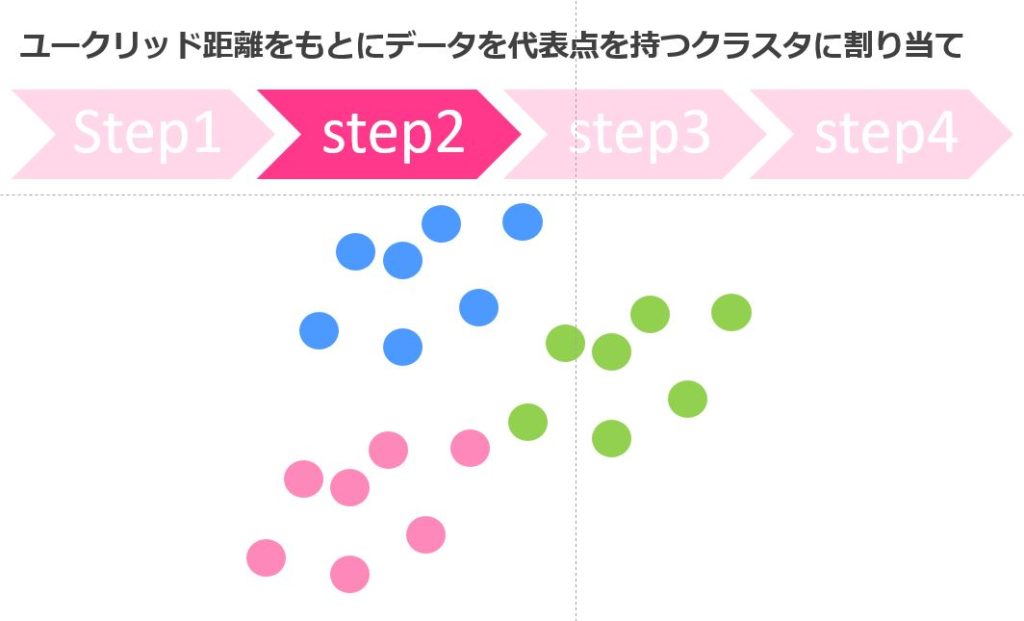
クラスター分析は、サンプルをいくつかの集団にグループ分けすることができる手法であり、教師なし学習として幅広く使われています。
クラスター分析には階層的クラスター分析と非階層的クラスター分析がありますが、大量のデータセットに対して用いるなら非階層的クラスター分析がオススメです。
こちらの記事にまとめています。

機械学習と統計学のおすすめ勉強法

最後にそんな機械学習と統計学の勉強法についてまとめておきましょう!
どちらも被っている部分は多いのですが、勉強すべき範囲や勉強におすすめの教材を紹介していきます!
是非参考にしてみてください!
もしどちらも網羅的に学びたいのであれば当メディアが運営するスクール「スタアカ(スタビジアカデミー)」がオススメです!
是非チェックしてみてください!
機械学習の勉強法
機械学習領域では、線形代数の勉強や微分の勉強をした後に各機械学習手法の理論の勉強に移るのがおすすめです。
そのためには以下のステップでの勉強がおすすめです。
・Udemyの「【初学者向け】データ分析コンペで楽しみながら学べるPython×データ分析講座(私の講座)」で機械学習の基礎をPython実装を理解
・Udemyの「【キカガク流】人工知能・機械学習 脱ブラックボックス講座ー初級編ー」で機械学習の理論のベースとなる微分を理解
・Udemyの「【キカガク流】人工知能・機械学習 脱ブラックボックス講座 – 中級編 –」で機械学習の理論のベースとなる線形代数を理解
・書籍の「はじめてのパターン認識」で機械学習の手法の理論を理解
・書籍の「これなら分かる最適化数学」で最適化手法を深堀り
この流れで勉強すれば間違いなく、理論と実践の両輪をある程度回しながら機械学習をしっかり身につけることが出来ると思います。
機械学習の勉強法について詳しくは以下の記事でまとめていますので是非チェックしてみてください!

統計学の勉強法
続いて統計学の勉強法では、記述統計と推計統計をおさえた上で簡単な多変量解析の勉強に進んでいくのがベターです。
統計学では以下のステップの勉強がおすすめです。
・Udemyの「【初学者向け】統計学の基礎をアニメーションを通じてビジネス観点で理解していこう!(私の講座)」で基礎を理解
・書籍の「入門統計解析法」で統計学理論について理解
・書籍の「多変量解析法入門」で多変量解析について理論的に理解
これである程度統計学について理論的に理解することができます。
詳しくは以下の記事でまとめていますのでこちらも合わせてチェックしてみてください!

機械学習と統計学の違い まとめ
本記事では、機械学習手法と統計学の違いについて見きました。
正直「この手法は機械学習で、この手法は統計学的手法だ」というのを覚えることには何の意味もありません。
機械学習と統計学的アプローチでは目的が違うのだということを念頭に置き、使い分けていきましょう。
・機械学習手法は精度追求型
・統計学的手法は解釈追求型
機械学習と統計学をしっかり学びたい方は当メディアが運営するスクール「スタアカ(スタビジアカデミー)」をチェックしてみてください!
スタアカ(スタビジアカデミー)
 公式サイト:https://toukei-lab.com/achademy/
公式サイト:https://toukei-lab.com/achademy/
| 【価格】 | ライトプラン:1280円/月 プレミアムプラン:149,800円 |
|---|---|
| 【オススメ度】 | |
| 【サポート体制】 | |
| 【受講形式】 | オンライン形式 |
| 【学習範囲】 | データサイエンスを網羅的に学ぶ 実践的なビジネスフレームワークを学ぶ SQLとPythonを組み合わせて実データを使った様々なワークを行う マーケティングの実行プラン策定 マーケティングとデータ分析の掛け合わせで集客マネタイズ |
データサイエンティストとしての自分の経験をふまえてエッセンスを詰め込んだのがこちらのスタビジアカデミー、略して「スタアカ」!!
当メディアが運営するスクールです。
24時間以内の質問対応と現役データサイエンティストによる複数回のメンタリングを実施します!
カリキュラム自体は、他のスクールと比較して圧倒的に良い自信があるのでぜひ受講してみてください!
他のスクールのカリキュラムはPythonでの機械学習実装だけに焦点が当たっているものが多く、実務に即した内容になっていないものが多いです。
そんな課題感に対して、実務で使うことの多いSQLや機械学習のビジネス導入プロセスの理解なども合わせて学べるボリューム満点のコースになっています!
ウォルマートのデータを使って商品の予測分析をしたり、実務で使うことの多いGoogleプロダクトのBigQueryを使って投球分析をしたり、データサイエンティストに必要なビジネス・マーケティングの基礎を学んでマーケティングプランを作ってもらったり・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践してもらったりする盛りだくさんの内容になってます!
・BigQuery上でSQL、Google Colab上でPythonを使い野球の投球分析
・世界最大手小売企業のウォルマートの実データを用いた需要予測
・ビジネス・マーケティングの基礎を学んで実際の企業を題材にしたマーケティングプランの策定
・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践して稼ぐ
機械学習と統計学をより詳しく知りたい・勉強したい方は以下の記事をご覧ください!