こんにちは！
データサイエンティストのウマたん(@statistics1012)です！
データ分析を行っていると以下のような場面にぶち当たることがあるのではないでしょうか？
そんな時に有用なのが「主成分分析」
主成分分析は、古くから使われている伝統的な手法ですが、現在も最前線で使われる強力な手法。
この記事では、そんな「主成分分析」について見ていき、最終的にはPythonでの実装を行っていきます。
以下のYoutube動画でも解説していますよ！
主成分分析とは
主成分分析は、1900年代前半にピアソンやホテリングにより導かれた手法であり、長い歴史を持っています。
Principal component analysis (PCA) in many ways forms the basis for multiv~ate data analysis
引用元：Google-“Principal Component Analysis”
教師データ（正解データ）がいらない手法であり、手元にあるデータの次元を圧縮し構造化するのに優れています。
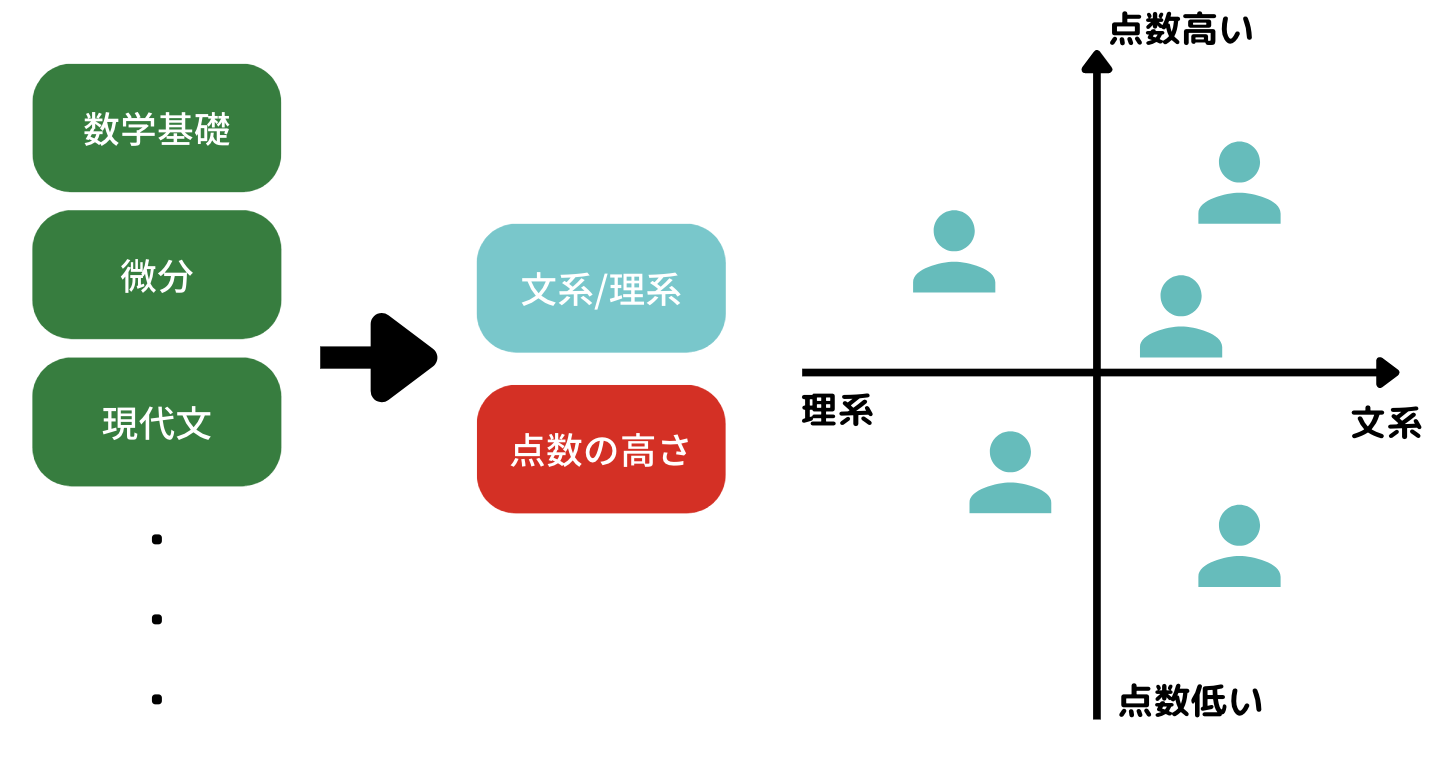
良く主成分分析の例として取り上げられるのが学校の成績の例。
生徒それぞれに対して算数・国語・理科・社会の点数が変数として存在します。
そんなデータセットに対して主成分分析をかけると、たとえば
・点数の高さを表した変数
・文系か理系かを表した変数
の2つに集約することができます。
元々4つあった変数を2つの変数に集約することでデータをより分かりやすく解釈できるようになる可能性があります。
この「2つ」という数字は恣意的に設定することが可能ですが、このようなデータセットであった場合は2つでほぼデータを説明できる結果になるはずです。
主成分軸によってデータをどのくらい説明できるか寄与率が算出されるのですが、概ね主成分軸の寄与率を足し上げていった時に80％を超えれば問題ないでしょう！
主成分分析のメリット
主成分分析のメリットは2つあります。
データの構造が分かりやすくなる
主成分分析を行うことで、データの構造を分かりやすくすることが可能です。
変数が多くデータの構造が分かりにくい時は、主成分分析をかけてみると良いでしょう。
次元圧縮により計算負荷を下げる
多次元データは計算負荷が物凄くかかります。
そんな多次元データに対して主成分分析をかけることにより、次元が圧縮され計算負荷が大幅に下がります。
先ほどの算数・国語・理科・社会だとあまり感じられないかもしれませんが、例えば、数学基礎・微分・線形代数・確率・現代文・古文・漢文・政治経済・現代社会・・・・
みたいな感じでものすごく多くの科目が合った場合、それを2つの軸に分けるとシンプルで分かりやすくなるということが実感できるでしょう。
主成分回帰（PCR）という手法が存在し、まさに多次元データへ適用される手法になっています。
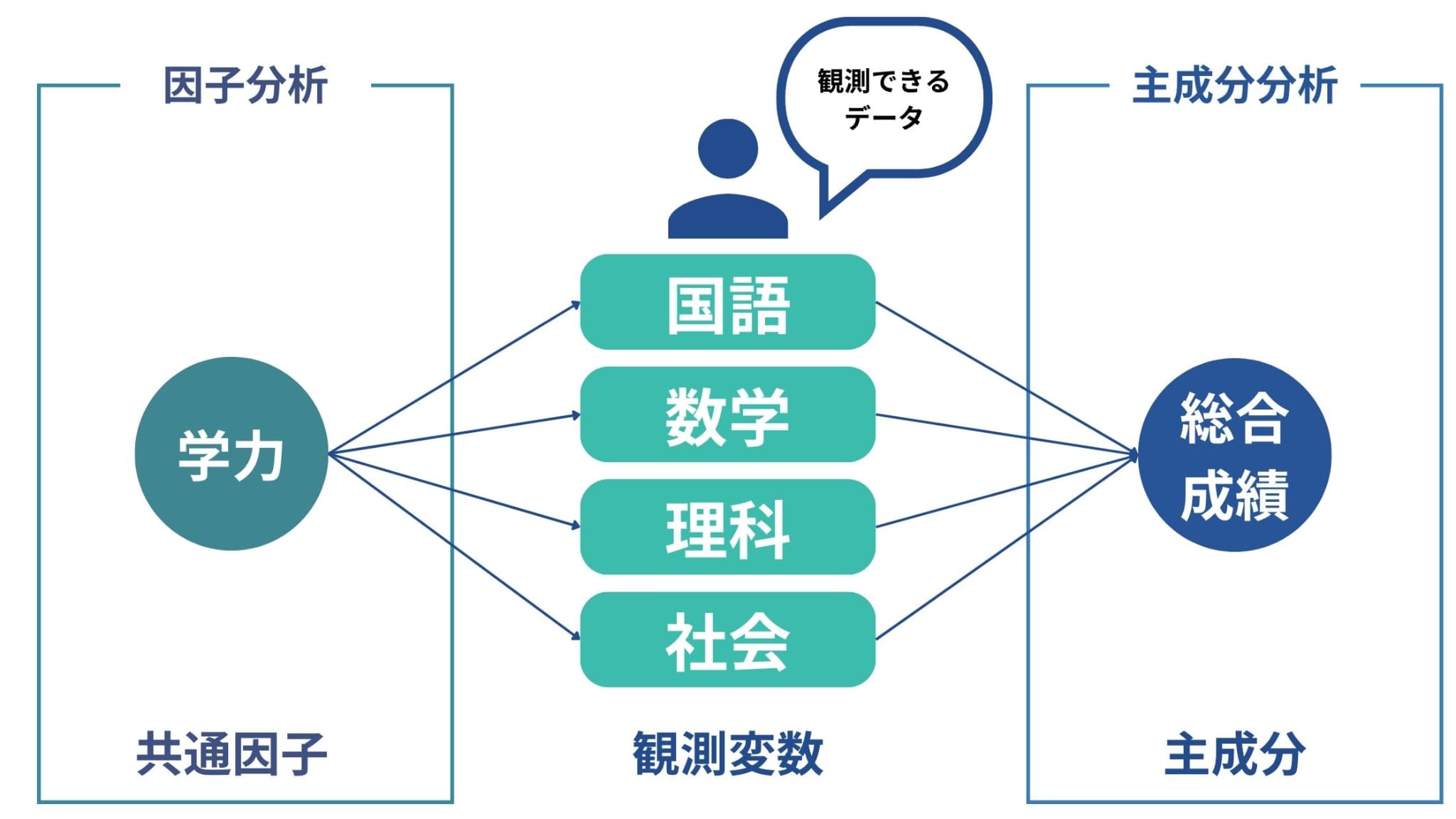
ちなみに主成分分析と似た手法に因子分析があります。
どちらも「より少ない変数にまとめる」というプロセスを辿りますが、両者の違いはズバリ分析の目的です。
因子分析が各観測変数から共通している部分を探索する分析であるのに対し、主成分分析は各観測変数をより少ない変数にまとめる分析です。
目的に合わせて分析手法を選択していきましょう！
・観測変数間の背後に存在する共通因子を見つけたい → 因子分析
・観測変数をより少ない変数にまとめたい → 主成分分析
因子分析について詳しくは以下の記事で解説しています！
主成分分析をPythonで実装してみよう！
それでは、最後にPythonで主成分分析を実装していきましょう！
非常に簡単に実装することが可能です。
使用するデータは、統計科学研究所の「成績データ」。以下のURLからダウンロードできます。
https://statistics.co.jp/reference/statistical_data/statistical_data.htm
| kokugo | shakai | sugaku | rika | ongaku | bijutu | taiiku | gika | eigo |
| 30 | 43 | 51 | 63 | 60 | 66 | 37 | 44 | 20 |
| 39 | 21 | 49 | 56 | 70 | 72 | 56 | 63 | 16 |
| 29 | 30 | 23 | 57 | 69 | 76 | 33 | 54 | 6 |
| 95 | 87 | 77 | 100 | 77 | 82 | 78 | 96 | 87 |
| 70 | 71 | 78 | 67 | 72 | 82 | 46 | 63 | 44 |
| 67 | 53 | 56 | 61 | 61 | 76 | 70 | 66 | 40 |
| 29 | 26 | 44 | 52 | 37 | 68 | 33 | 43 | 13 |
9科目の点数が166人分入ってます。
主成分分析自体は、scikit-learn内のライブラリを用います。
from sklearn.decomposition import PCA
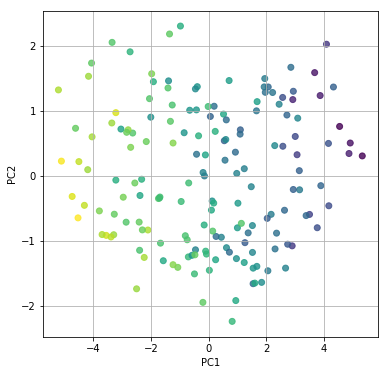
実際に第1主成分と第2主成分を軸にデータをプロットしてみるとこんな感じ
寄与率を見てみると以下のようになっており、ほぼ第2主成分までで80％を超えていることが分かります。
array([0.66738119, 0.12202057, 0.05453805, 0.04521959, 0.03336222, 0.02460657, 0.02030967, 0.01902168, 0.01354047])
Pythonの学習については以下にまとめていますので合わせて参考にしてみてください。
主成分分析 まとめ
主成分分析について簡単に見てきました。
最後に主成分分析についてまとめておきましょう！
■データの構造を分かりやすく出来る
■次元圧縮により計算負荷を下げることが出来る
■Pythonで簡単に実装できる
主成分分析は様々な場面で活用できる優秀な手法です！
もし主成分分析について詳しく知りたい方はこちらの書籍がオススメ！
是非参考にしてみてください！
多変量解析手法については以下の記事でより詳しくまとめていますので見てみてください！
統計学や機械学習やデータサイエンスの勉強法については以下の記事をぜひ参考にしてみてください！
ちなみにもし、これらを全て包括的に学びたいのであれば当メディアが運営するスクールであるスタビジアカデミー、略して「スタアカ」がオススメです！
イラスト出典：Illustration by Stories by Freepik
スタビジのコンテンツをさらに深堀りしたコンテンツが動画と一緒に学べるスクールです。
プレミアムプランでは私がマンツーマンで伴走させていただきます！ご受講お待ちしております！
