統計モデリングとは何か?線形モデルから階層ベイズまでをわかりやすく解説

統計モデリングと聞くと非常に堅苦しいイメージを持つかもしれませんが、統計を語る上で非常に重要な考え方なんです。
この記事では、そんな統計モデリングを出来るだけ簡単に説明していきます!
回帰分析と非常に関係が深いので、先に以下の記事を読んでみることをオススメします。

この記事では、通称「緑本」と呼ばれている以下の本を参考にしています。
非常に読みやすく分かりやすいので一読することをオススメします。
最も単純な線形モデルから順に拡張されたモデルを紹介していきますよー!
目次
統計モデリングとはそもそも何か
まずは、統計モデリングとは何か・統計モデリングがなぜ必要か見ていきましょう!
普段なんとなーく線形回帰分析を使っていませんか?
実は線形回帰分析というのは目的変数の分布に正規分布を仮定しているという制限があるのです。
ビジネスシーンで使われるデータは正規分布に従っていないことが多く、それらを分析に用いる時は注意が必要です。
ちなみに以下のようにBox-cox変換を用いることで無理やり正規分布に近似させる方法もあります。

そこで重要なのが、そのデータに合ったモデルを定義すること。
すなわちそれが統計モデリング。
ポアソン回帰やロジスティック回帰などは統計モデリングの初歩的手法ですね。
ただ、ここで大事なのは複雑な手法を知ることではありません。
世の中のデータの真値に完璧に一致する分布など存在しません。
いかに手元にあるデータからそのデータの母集団分布をコスパ良くモデリングすることができるか。
必ずしも複雑なモデリングをすれば良いというわけではないので注意が必要です。
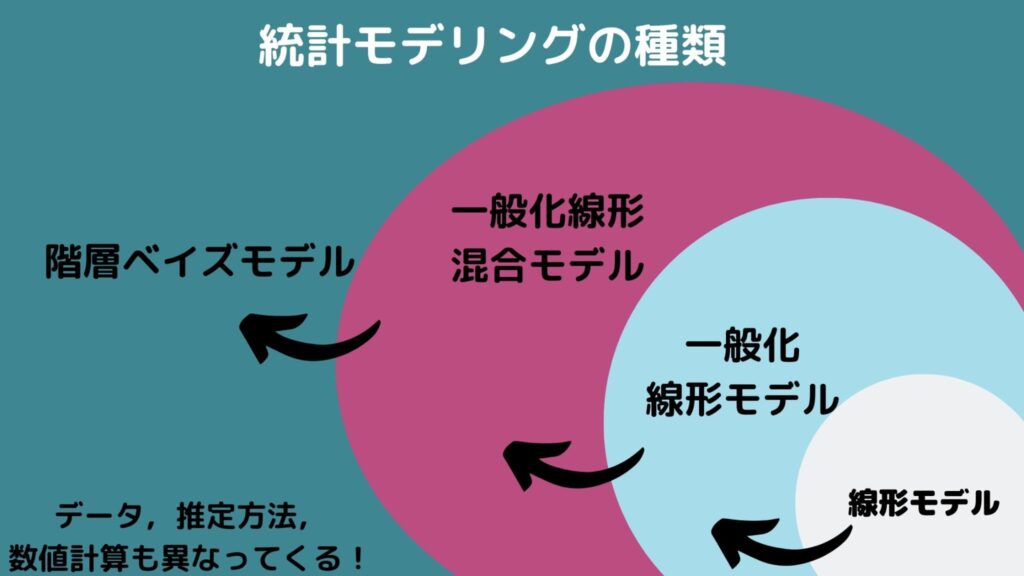
統計モデリングの種類
まず、いくつかのモデリングのステップがあることを覚えておきましょう。
線形モデル(単回帰分析)
↓
一般線形モデル(よく使う重回帰分析とか)
↓
一般化線形モデル(ポアソン回帰・ロジスティック回帰とか)
↓
一般化線形混合モデル
↓
階層ベイズ
下に行けば行くほどモデリングが複雑になってきます。
正直、一般化線形モデルまではビジネスシーンで使いますがそれ以降はあまり使う場面はないかもですね。
統計モデリング①:線形モデル
線形モデルは次の式で表されます。
\begin{eqnarray*}
{y_i}&=&{{\bf x}_i^T}{\beta}+{\epsilon_i},{\epsilon_i}\sim N(0,\sigma^2)\
\end{eqnarray*}
線形モデルの特徴は\({\bf x}_i\)を与えた時の\(y_i\)の条件付き分布が正規分布に従うというところです。特に、誤差分散が全ての\(i\)に対して同一である場合に限ります。すなわち、次の様になります。
\begin{eqnarray*}
{y_i}|{\bf x_i}\sim N({{\bf x}_i^T}{\beta},\sigma^2)\
\end{eqnarray*}
いわゆる通常の単回帰分析のモデルですね。パラメータは通常の最小二乗法で推定します。
統計モデリング②:一般線形モデル
一般線形モデルは線形モデルの拡張であり次の式で表されます。
\begin{eqnarray*}
{\bf Y}&=&{\bf X}{\bf B}+{\bf E},{\epsilon_i}\sim MVN({\bf 0},{\bf Sigma})\
\end{eqnarray*}
\({\bf X}\)は計画行列を表します。
一般線形モデルの特徴は\({\bf X}\)を与えた時の\({\bf Y}\)の条件付き分布が多変量正規分布に従うというところです。特に、誤差分散共分散行列が任意の正定値対称行列になります。パラメータは(重み付き)最小二乗法で推定します。
線形モデルから一般線形モデルへと拡張することで重回帰分析・分散分析・共分散分析などを同じモデルとして表すことが出来ます。
それだけでなく、目的変数が複数の場合である、多変量重回帰分析や多変量分散分析もこのモデルで表されます。
多変量重回帰分析は、詳細な日本語の文献もほとんどないんですよね・・
統計モデリング③:一般化線形モデル
線形モデルでは、目的変数は正規分布を仮定していました。
しかし、世の中のデータには正規分布に従うとは考えづらいデータも多く存在します。
そこで、さらに拡張されたものが一般化線形モデルです。
例えば、「\(n_i\)個体中\(y_i\)個体が生存した」というのを目的変数とする場合には、目的変数が二項分布に従うロジスティック回帰モデルになります。
ロジスティック回帰モデルは次の式で表されます。
\begin{eqnarray*}
&&{y_i}|{p_i}\sim B(n_i,p_i)\
&&log\left(\frac{p_i}{1-p_i}\right)={{\bf x}_i^T}{\beta}\
\end{eqnarray*}
他にも例えば、「アイスが\(y_i\)個売れた」というのを目的変数とする場合には、目的変数がポアソン分布に従うポアソン回帰モデルになります。
\begin{eqnarray*}
&&{y_i}|{\lambda_i}\sim Po(\lambda_i)\
&&\log(y_i)={{\bf x}_i^T}{\beta}\
\end{eqnarray*}
一般化線形モデルでは、パラメータは最尤法で推定します。
統計モデリング④:一般化線形混合モデル
一般化線形混合モデルは、サンプルに個人、場所、時間などのグループ構造が存在する場合にグループ間の差による変動も組み込んだモデルです。
例えば、次の様なデータを想定します。業界別に「経常利益」・「純資産」・「一年以内に倒産したか」を集めたデータです。
このデータから倒産予測モデルを作りたいと考えます。
表:倒産データ
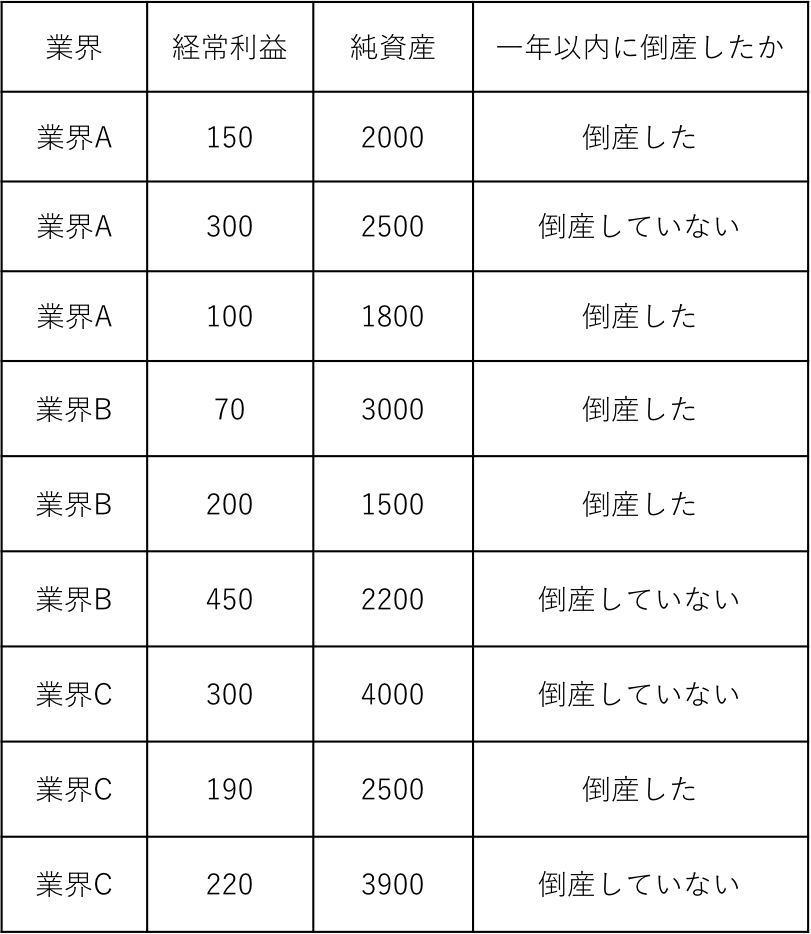
このデータでは、目的変数は「一年以内に倒産したか」という二値のデータになるので、二項分布に従うと考え、ロジスティック回帰を適用しようとします。
しかし、感覚的には業界によって倒産のしやすさも異なってくると考えられます。
つまり、「業界間の変動」を考慮する必要があります。
通常のロジスティック回帰である一般化線形モデルでは、この「業界間の変動」は存在しないものとしてモデル化してしまいます。そこで、一般化線形混合モデルを用います。
各企業\(i\)について、\(y_i\)を「一年以内に倒産したか」、\(x_{i1}\)を「経常利益」、\(x_{i2}\)を「純資産」とすると、次の様なモデルになります。
\begin{eqnarray*}
&&{y_i}|{p_i}\sim B(1,p_i)\
&&log\left(\frac{p_i}{1-p_i}\right)={{\bf x}_i^T}{\beta}+{r_j}\
&&{r_j}\sim N(0,s^2)\
\end{eqnarray*}
ここで、\(r_j\)は「業界間の変動」を表す変量効果であり今は正規分布を仮定しています。\(j\)は業界を表します。
一般化線形混合モデルでは、パラメータを推定する時、\(r_j\)も推定しようとするとパラメータの数が多すぎ最尤法では不安定になったり、そもそも最尤法では推定出来ないこともあります。推定したいのは\(beta\)だけなので\(beta\)のみを推定することにします。
その方法は積分によって\(r_j\)を消し去ることです。そうすることで、\(beta\)と\(r_j\)の正規分布のパラメータ\(s\)のみになり、最尤推定することが出来ます。
しかし、変量効果が多くなると消し去るパラメータの数も多くなります。
すると、その分だけ積分回数も増えてしまいます。
多重積分は計算時間もかかり、推定も不安定になります。
そこで、MCMCを用いる階層ベイズモデルが必要になります。
統計モデリング⑤:階層ベイズモデル
階層ベイズモデルは一般化線形混合モデルをベイズ化したものになります。
一般化線形混合モデルの説明で、変量効果が多くなった時にはMCMCを用いるのが良いと述べました。
MCMCはベイズの一つではありませんが、ベイズと深く関わるものです。
そこで、一般化線形混合モデルをベイズ統計学の枠組みで再構築したものが階層ベイズモデルになります。
ベイズ統計学に関しては以下の動画も参考にしてみてください!
ベイズ統計学ではパラメータも確率変数であると考えます。
すなわち、ただ一つの真値を持つのではなく、何かしらの確率分布に従うと考えます。
先ほどの例でいうと、\(r_j\)が正規分布に従うと考え、\(r_j\)のパラメータ\(s\)がさらに何かしらの分布に従うと考えます。
倒産予測モデルのパラメータの関係を図にして表してみます。
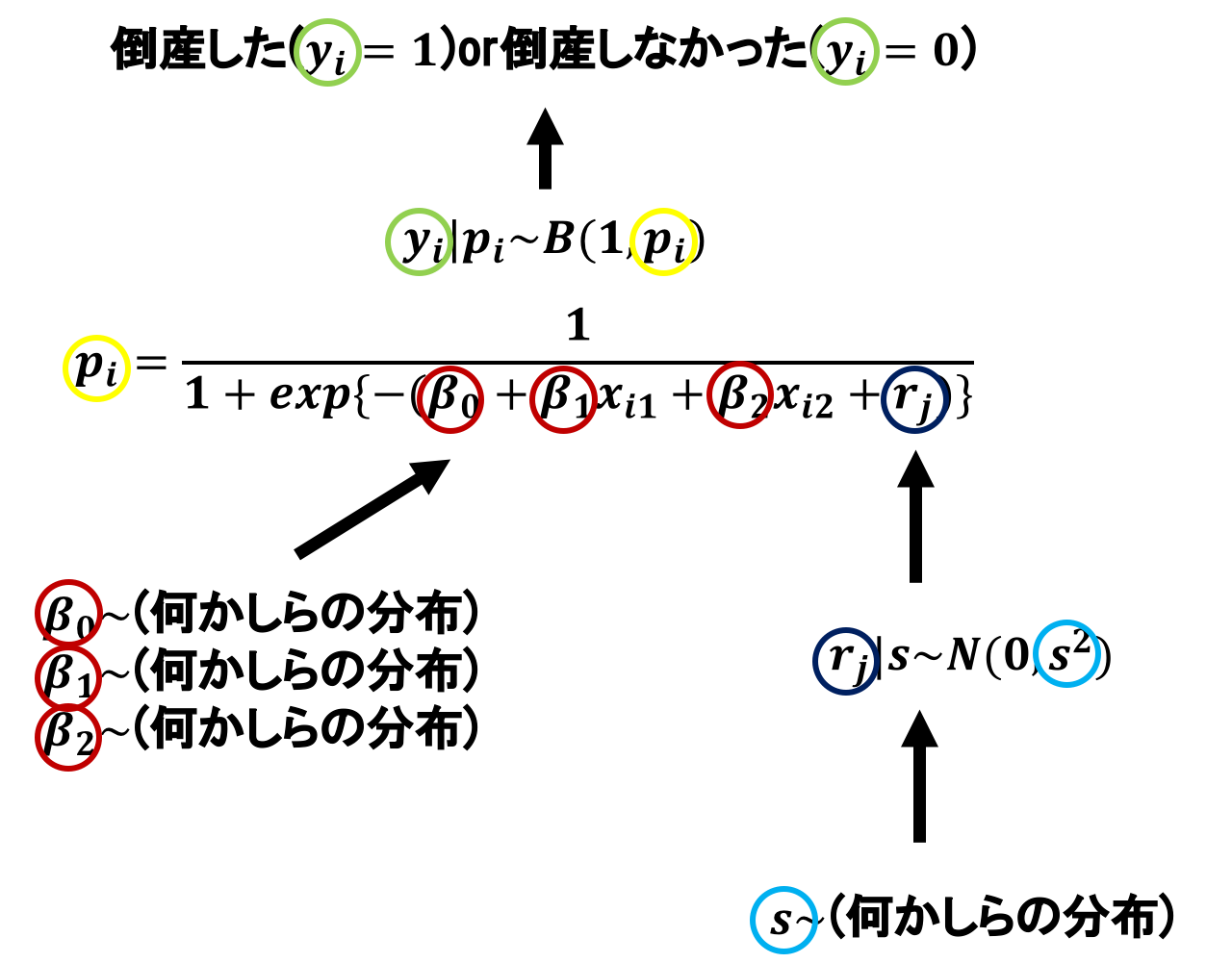
図:階層のイメージ
この図の様に、「パラメータのパラメータのパラメータの…」という様に「階層化」されるため階層ベイズモデルと呼ばれます。
統計モデリングを実装するには
統計モデリングを実装するにはどうすれば良いか。
基本的に一般化線形モデルまでは、RもしくはPythonに入っている関数を使えば簡単に実装することが可能です。
しかし、階層ベイズを使い複雑なモデリングを行いたい場合はStanという新たなモデリングツールを使うことをオススメします!
Stanはあまり良い書籍が出ていないのですが、以下の本はオススメです!
R×Stanを勉強したいなら絶対目を通しておくべきです。
Stanを勉強する上でのオススメ本は以下にまとめていますので良ければご覧ください!

Stan×Pythonなら以下のUdemy講座が圧倒的におすすめです!
この教材では、ベイズの基本的な概念から階層ベイズまでPythonとStanを使いながら実装していきます。
理論と実装が分かりやすく学べるので非常におすすめなんです!
なかなかStanが学べる教材はないので貴重です。
Pythonの勉強は以下の記事を参考にしてみてください!

Pythonやデータサイエンス全般について学びたい方は当メディアが運営するサービス「スタアカ」を是非チェックしてみてください!
網羅的に学べます!
統計モデリング まとめ
本記事では、統計モデリングについてみてきました。
最後にまとめておきましょう!
■統計モデリングの種類
・線形モデル
・一般線形モデル
・一般化線形モデル
・一般化線形混合モデル
・階層ベイズモデル
■統計モデルは解析したいデータの特徴にあわせて選ぶ必要がある
・目的変数は連続変量か離散変量か?
・正の値のみか負の値も取るか?
・上限や下限はあるか?
・データにグループによる変動(変量効果)は存在するか?
・変量効果はいくつあるのか?
■モデルと推定方法の関係
線形モデル・一般線形モデル:最小二乗推定
一般化線形モデル・一般化線形混合モデル:最尤推定
階層ベイズモデル:ベイズ推定
■推定を実現する数値計算方法
最尤推定:ニュートン法・準ニュートン法
ベイズ推定:MCMC
以下の本を読めば線形モデルから階層ベイズまでの流れをスムーズに理解することができます。
この本は圧倒的にオススメなので是非読んでみてください!
ここから統計学の勉強・機械学習の勉強に進みたいなら以下の記事をチェックしてみてください!



























