ロジスティック回帰の理論とRによる実装方法を徹底解説!
データサイエンティストのウマたん(@statistics1012)です!
一般化線形モデルの一つである、ロジスティック回帰。
有名であり基本的な手法ですが、実務でもよく使われる汎用性の高い手法です。
ロジスティック回帰は多変量解析という分野以外に機械学習という枠組みでも基本的な手法として出てきます。
この記事では、そんなロジスティック回帰について見ていきたいと思います。
・ロジスティック回帰を用いる場面
・ロジスティック回帰の計算方法
・ロジスティック回帰の実装
・ロジスティック回帰の勉強法
目次
ロジスティック回帰の適用場面

回帰分析は目的変数に負の値でも正の値でもとる連続変量を考えていました。
より正確にいうと、線形回帰において説明変数\(x_i\)を与えた時の\(y_i\)の条件付き分布には正規分布を仮定しています。
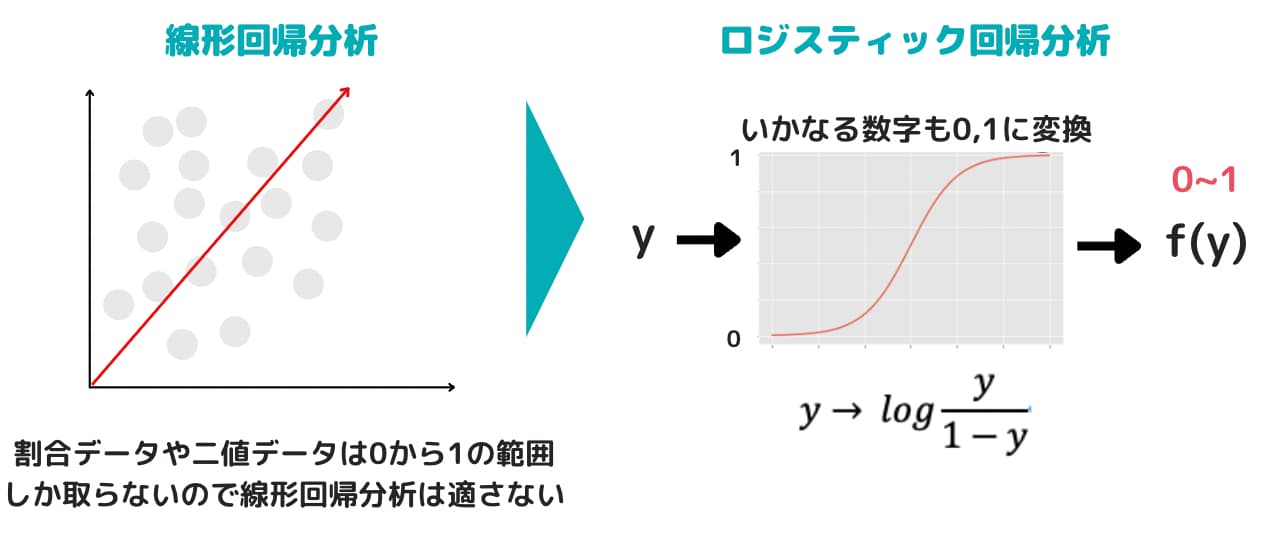
しかし、世の中には、「100人中70人の病気が治った。」や「ある会社が倒産したかどうか」などの割合データや二値データが存在します。
どちらも、値は0から1の範囲しかとりません。
この時、線形回帰を行うとどうなるでしょうか。
推定された目的変数は負の値になったり1を超える場合もあり、扱いに困ってしまいます。
そんな時に用いる方法がロジスティック回帰です。
以下の動画でも解説していますので是非チェックしてみてください!
その他の手法含む機械学習系、その他のAI用語を一挙にまとめた以下の記事も合わせて要チェックです!

ロジスティック回帰モデル
それでは、具体的にロジスティック回帰モデルとは何なのか見ていきましょう
Using components of linear regression reflected in the logit scale, logistic regression iteratively identifies the strongest linear combination of variables with the greatest probability of detecting the observed outcome.
引用元:Google-“Logistic Regression: A Brief Primer”
ロジスティック回帰が用いられる場面は目的変数が二値もしくは割合データの場合です。
二値や割合データが従う分布として最も考えられやすいものは二項分布です。
例えば、「\(m_i\)個体中\(y_i\)個体が生存した」というデータは、\(B(m_i,p_i)\)に従うと考えます。この時、\(p_i\)が未知パラメータになります。
この\(p_i\)と\({\bf x}^T\beta\)(線形予測子と呼びます。)を紐付ける関数を考えてみましょう。
\(p_i\)は0から1の範囲の値しか取らないので、\({\bf x}_i^T\beta\)が正の無限大になっても負の無限大になっても0~1の範囲に収まっており、また、単調な関数が良いです。そこで、次の様な関数を用いて\(p_i\)と紐付けます。
\begin{eqnarray*}
p_i&=&\frac{1}{1+exp(-{\bf x}_i^T\beta)}\\
\end{eqnarray*}
この右辺の関数のことをロジスティック関数と呼びます(だからロジスティック回帰)。
こうすることで、\(\beta\)を求めれば\(p_i\)が分かり、\(y_i\)の従う分布を把握できる様になりました。
では次に、どの様にして\(\beta\)を求めていくかを考えていきます。
先ほどの式を右辺が\({\bf x}_i^T\beta\)だけになる様に変換すると下の式の様になります。
\begin{eqnarray*}
log\left(\frac{p_i}{1-p_i}\right)&=&{\bf x}_i^T\beta\\
\end{eqnarray*}
左辺は\(p_i\)を\(1-p_i\)で割って対数をとったものになっています。\(p_i\)を成功の確率と解釈すれば、\(1-p_i\)は失敗の確率と捉えることができます。
この\(\frac{p_i}{1-p_i}\)はオッズと呼ばれます。オッズは結果の解釈で重要になるので後で改めて説明します。
また、オッズの対数をとるこの変換をロジット変換と呼び、\(logit(p_i)\)とも表したりします。
この変換によって、回帰分析っぽくなりました。
さて、ここから\(\beta\)の推定に入っていきます。
\(\beta\)の推定方法

ロジット変換によって回帰分析っぽい式になりました。
ロジスティック回帰では\(\beta\)の推定方法は重み付き最小二乗法と最尤法の二種類があります。
重み付き最小二乗法
最小二乗法によって\(\beta\)の推定を行いたいのですが、最小二乗法を用いる時によいとされるのは目的変数の条件付き分布がサンプルに対して等分散の正規分布に従うと考えられる時です。
ここで、\(logit(p_i)\)の分布を考えてみましょう。
まず、得られているデータから\(p_i\)を作るため\(p_i=\frac{y_i}{m_i}\)とします。\(y_i\)は二項分布に従うと考えているため、期待値と分散は次の様になります。\begin{eqnarray*}
E[y_i]&=&m_ip_i\\
V[y_i]&=&m_ip_i(1-p_i)\\
\end{eqnarray*}
次に、\(logit(p_i)=log\left(\frac{p_i}{1-p_i}\right)=log\left(\frac{y_i}{m_i-y_i}\right)\)の分散をデルタ法で近似します。
\begin{eqnarray*}
log\left(\frac{p_i}{1-p_i}\right)\approx \frac{1}{m_ip_i(1-p_i)}
\end{eqnarray*}
二項分布と正規分布の性質より\(m_ip_i(1-p_i)\)が十分大きい時、正規分布に従うと見なせます。
そして、重み\(\sqrt{w_i}=\sqrt{m_ip_i(1-p_i)}\)を\(logit(p_i)\)にかけることで、等分散性を確保してから最小二乗法を行います。
重みを付けているため重み付き最小二乗法と呼びます。
最尤法
重み付き最小二乗法は複雑な計算も必要なく手計算でも可能ですが、一つ大きな問題があります。それは、\(m_i=1\)である時の二値データでは解析できないことです。
無理やり解析しても結果は不安定なものになります。そこで、現在ではコンピュータの発展により最尤法による推定が主流です。
目的変数は二項分布に従うというところから、尤度関数を導きます。
同時確率関数は
\begin{eqnarray*}
\displaystyle \prod_{ i = 0 }^n \binom{ m_i }{ y_i }p_i^{y_i}(1-p_i)^{m_i-y_i}&=&exp\left[\displaystyle \sum_{ i = 1 }^{ n } {y_i}log\left(\frac{p_i}{1-p_i}\right)+{m_i}log\left(1-p_i\right)+log\binom{ m_i }{ y_i }\right]\\
\end{eqnarray*}
となるので、対数尤度関数は
\begin{eqnarray*}
l({\bf p};{\bf y})&=&\displaystyle \sum_{ i = 1 }^{ n } {y_i}log\left(\frac{p_i}{1-p_i}\right)+{m_i}log\left(1-p_i\right)+log\binom{ m_i }{ y_i }\\
\end{eqnarray*}
ここから、\(p_i\)を\({\bf x}_i^T\beta\)の式の方で書き直して、パラメータを\(\beta\)のみにします。
そして、微分することで\(\beta\)を推定します。
この計算は式で綺麗に求めるのは難しいためニュートン法などの数値計算方法を用いる必要があります。
ロジスティック回帰の結果解釈

得られた\(\beta\)をどの様に解釈すれば良いでしょうか。
線形回帰であれば、偏回帰係数は他の変数が一定である基でその変数を1単位増加させた時に目的変数へ与える影響を表していました。
しかし、ロジスティック回帰の場合では、\(\beta\)の大きさがロジスティック関数で変換されるので、よく分かりません。
そこで、オッズを使って解釈します。説明変数が3個のモデルで左辺をオッズにした式を下に示します。
\begin{eqnarray*}
\frac{p_i}{1-p_i}&=&exp\left(\beta_0+\beta_1x_i1+\beta_2x_i2+\beta_3x_i3\right)\\
\end{eqnarray*}
ここで、変数1が1単位増えた時の式は次の様になります。
\begin{eqnarray*}
\frac{p_i^*}{1-p_i^*}&=&exp\left(\beta_0+\beta_1(x_i1+1)+\beta_2x_i2+\beta_3x_i3\right)\\
&=&exp\left(\beta_1\right)exp\left(\beta_0+\beta_1x_i1+\beta_2x_i2+\beta_3x_i3\right)\\
\end{eqnarray*}
すると、変数1が1単位増える前の式との関係は次の様になります。
\begin{eqnarray*}
\frac{p_i^*}{1-p_i^*}&=&exp\left(\beta_1\right)\frac{p_i}{1-p_i}\\
\end{eqnarray*}
すなわち、「変数1が1単位増えるとオッズ比が\(exp(\beta)\)倍になる。」という解釈ができます。
ロジスティック回帰で実際にデータ分析

続いて、ロジスティック回帰モデルの人工データを用いてロジスティック回帰・Lasso・Ridgeの精度比較を行います。
Lasso・Ridgeは回帰分析の一種でスパースなデータセットに対して効果的です。
スパース推定に関してはこちらの記事にまとめていますのであわせてご覧ください!

実験の設定と手順
・比較手法:通常のロジスティック回帰・Lasso回帰・Ridge回帰
・評価指標:テストデータの平均誤判別率
・シミュレーション回数:100回
実験の流れは簡単にこんな感じです。
- 人工データを生成
- データを解析
- 指標を算出して結果を格納
- 1~3を100回繰り返す
- 結果の平均とばらつきで比較
人工データ生成
今回のデータの生成モデルを次に示します。
\begin{eqnarray*}
y_i&\sim&B(m_i,q_i)\\
m_i&=&1\\
q_i&=&\frac{1}{1+exp(-1-{\bf x}_i^T{\bf \beta})}\\
{\bf \beta}&=&(1,-1,0,\cdots,0)^T\in {\bf R}^p\\
{\bf x_i}&\sim& N({\bf \mu},{\bf \Sigma})\\
{\bf \mu}&=&{\bf 0}_p\\
{\bf \Sigma}&=&{\bf I}_p\\
i&=&1,2,\cdots,n\\
\end{eqnarray*}
線形回帰のときと同様で、説明変数は\(p\)次元であり、平均0・独立で発生させています。
また、\(\beta\)は\(p\)次元ベクトルであり、変数1と変数2のみが目的変数へ寄与があります。
つまり、かなりスパースな設定になっています。
今回は、\(p\)を5,10,50と変化させて実験してみます。
シミュレーション実験
シミュレーション実験をしてみましょう。
サンプルサイズ\(n\)は1100とします。
100個のデータを学習データ、残りの1000個のデータをテストデータとして実験します。
今回用いるコード(\(p=50\)の場合)を載せておきます。
実行する前に入っていないパッケージはインストールしておいてください。
ばらつきも含めて見たいので結果を箱ひげ図で表します。
通常のロジスティック回帰はglmと表記してあります。
・\(p=5\)の結果

やはり説明変数の数も多くないのでどの手法も同程度ですね。
・\(p=10\)の結果
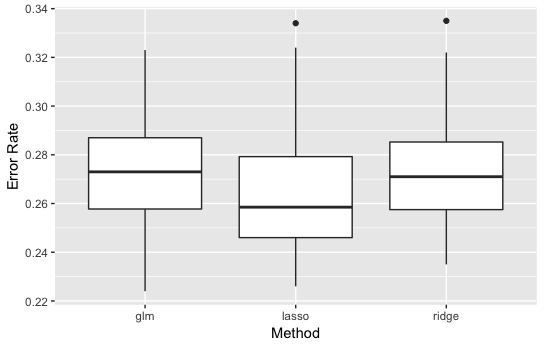
Lassoが少し良い精度を示しているように見えます。
・\(p=50\)の結果
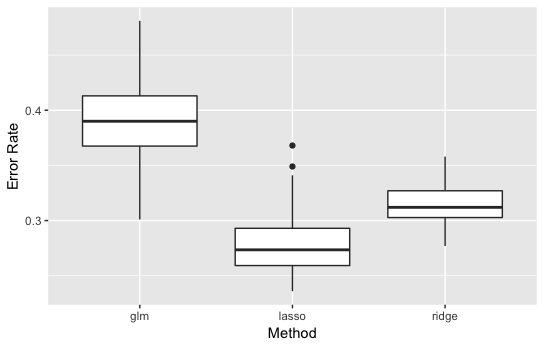
かなり、差が出ました。
線形回帰のときと同様でLassoタイプのロジスティック回帰が最も良くなりました。
また、実行してみるとglm()では\(p=50\)のとき警告メッセージが出てきてしまいます。これは、変数の数が多くて推定が不安定になったからと考えられます。
どうでしょうか。結果は予想通りでしたね!
精度比較の結果よりシミュレーションでロジスティック回帰モデルのデータの作り方や実際の解析の仕方を伝えたかったので分かっていただけたら嬉しいです!
ロジスティック回帰の勉強法

ロジスティック回帰の理論と実装について見てきました。
より深く知りたい方に向けてロジスティック回帰のおすすめ勉強法を紹介していきます。
理論を書籍で勉強
理論に関しては書籍にエッセンスが詰まっていますので、書籍を用いて勉強することをオススメします。
以下の2冊がオススメ!
特にデータ解析のためのモデリング入門は通称緑本と呼ばれていて、ロジスティック回帰などの一般化線形モデリングから階層ベイズなどの統計モデリングの応用まで幅広く学べる良書です。
実装をWebサービスで勉強
書籍で勉強だけしていてもイメージがわかないと思うので是非当メディアが運営する以下のスクール「スタアカ(スタビジアカデミー)」で手を動かしながら学んでみてください!
 公式サイト:https://toukei-lab.com/achademy/
公式サイト:https://toukei-lab.com/achademy/
| 【価格】 | ライトプラン:1280円/月 プレミアムプラン:149,800円 |
|---|---|
| 【オススメ度】 | |
| 【サポート体制】 | |
| 【受講形式】 | オンライン形式 |
| 【学習範囲】 | データサイエンスを網羅的に学ぶ 実践的なビジネスフレームワークを学ぶ SQLとPythonを組みあわせて実データを使った様々なワークを行う マーケティングの実行プラン策定 マーケティングとデータ分析の掛け合わせで集客マネタイズ |
データサイエンティストとしての自分の経験をふまえてエッセンスを詰め込んだのがこちらのスタビジアカデミー、略して「スタアカ」!!
当メディアが運営するスクールです。
24時間以内の質問対応と現役データサイエンティストによる複数回のメンタリングを実施します!
カリキュラム自体は、他のスクールと比較して圧倒的に良い自信があるのでぜひ受講してみてください!
他のスクールのカリキュラムはPythonでの機械学習実装だけに焦点が当たっているものが多く、実務に即した内容になっていないものが多いです。
そんな課題感に対して、実務で使うことの多いSQLや機械学習のビジネス導入プロセスの理解などもあわせて学べるボリューム満点のコースになっています!
ウォルマートのデータを使って商品の予測分析をしたり、実務で使うことの多いGoogleプロダクトのBigQueryを使って投球分析をしたり、データサイエンティストに必要なビジネス・マーケティングの基礎を学んでマーケティングプランを作ってもらったり・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践してもらったりする盛りだくさんの内容になってます!
・BigQuery上でSQL、Google Colab上でPythonを使い野球の投球分析
・世界最大手小売企業のウォルマートの実データを用いた需要予測
・ビジネス・マーケティングの基礎を学んで実際の企業を題材にしたマーケティングプランの策定
・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践して稼ぐ
ロジスティック回帰 まとめ
本記事では。ロジスティック回帰について見てきました!
最後に簡単にまとめておきましょう!
・ロジスティック回帰とは目的変数が二値もしくは割合データの場合に用いる回帰分析である!
・パラメータの推定方法は重み付き最小二乗法か最尤法がある!
・結果の解釈はオッズを用いる!
ロジスティック回帰を勉強した後は、統計学をより深めるか様々な機械学習手法を学ぶか、より広範にデータサイエンスを学ぶとよいでしょう!
以下の記事をぜひ参考にしてみてください!



























