共分散構造分析をわかりやすく解説!Pythonでパス図を出力してみよう!

こんにちは!スタビジ編集部です!
データを分析する際、以下のような問題に直面することがあるのではないでしょうか?
そんな時に有用なのが共分散構造分析(SEM : Structural Equation Modeling)。
共分散と呼ばれる数値を利用して、変数間の因果関係をモデル化することができます。
この記事では、そんな共分散構造分析の特徴とPythonでの実装を見ていきたいと思います。
以下のYoutube動画でも解説しているのであわせてチェックしてみてください!
目次
共分散構造分析とは

共分散構造分析とは多変量解析の分析手法のひとつであり、直接観測できない「潜在変数」と直接観測できる「観測変数」の因果関係をモデル化することができる手法です。
解析によって、因果関係の向きや強さを明らかにすることができます。
例えば、以下のようなワインの満足度に関するアンケートデータが手元にあるとしましょう。
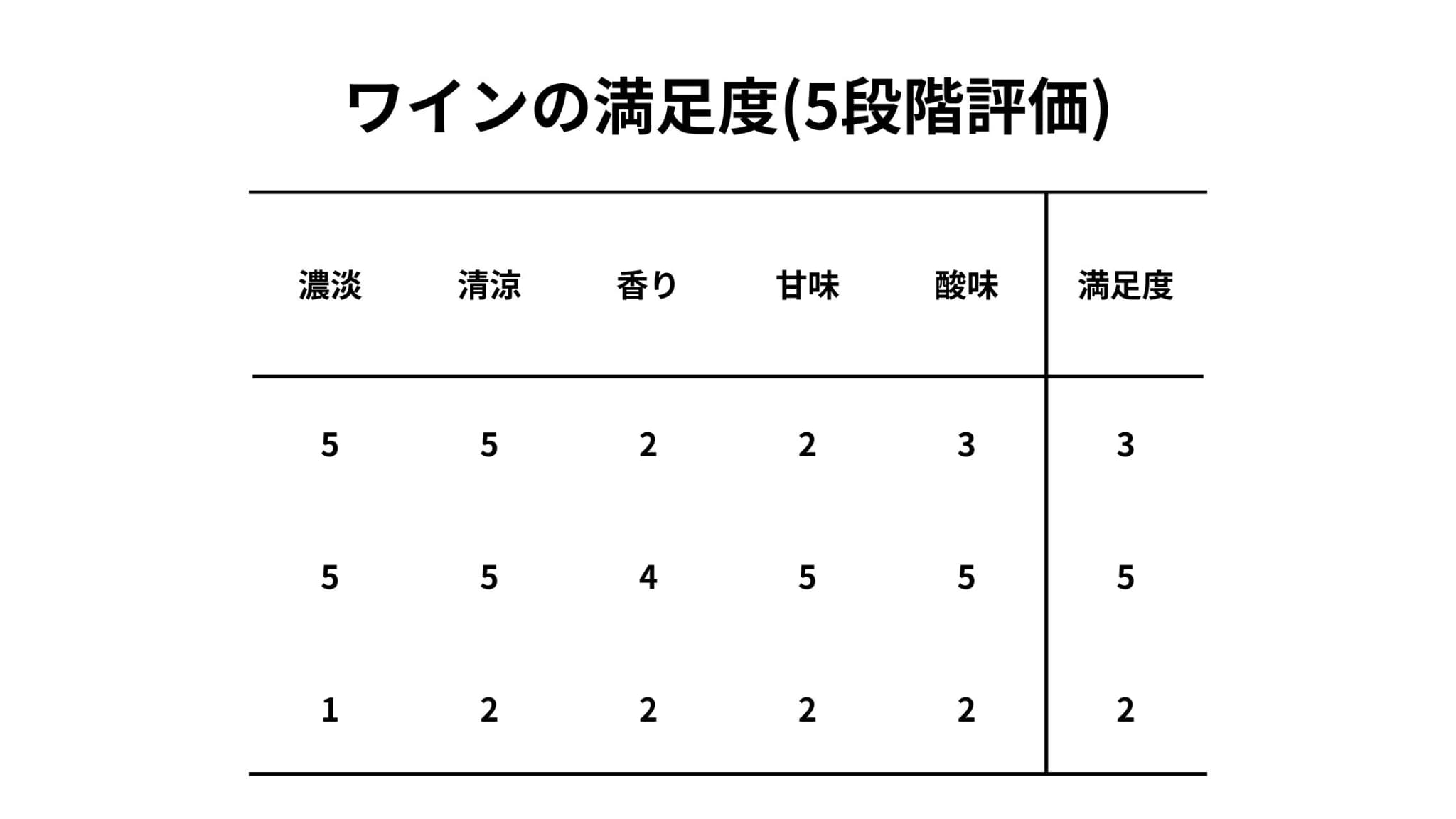
5つの評価項目と満足度で構成されていることがわかります。
一般的に、ワインのおいしさ(満足度)は色の濃淡や清涼感などの「見た目」と、香りや甘味、酸味などの「風味」によって評価されるという因果関係が考えられます。
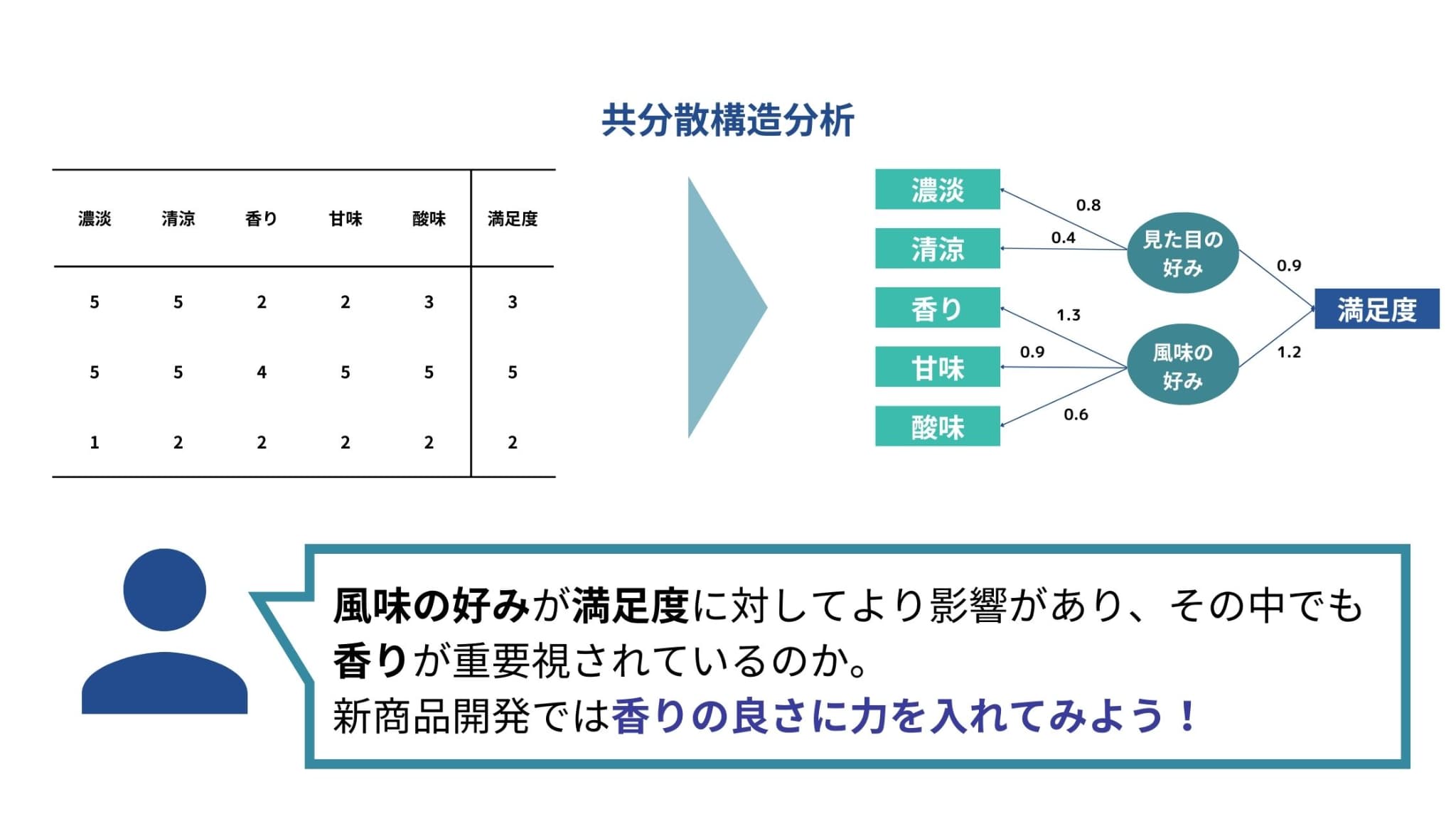
そこで、「見た目」と「風味」という潜在変数があるという仮説を立て、共分散構造分析を行ってみます。
すると、
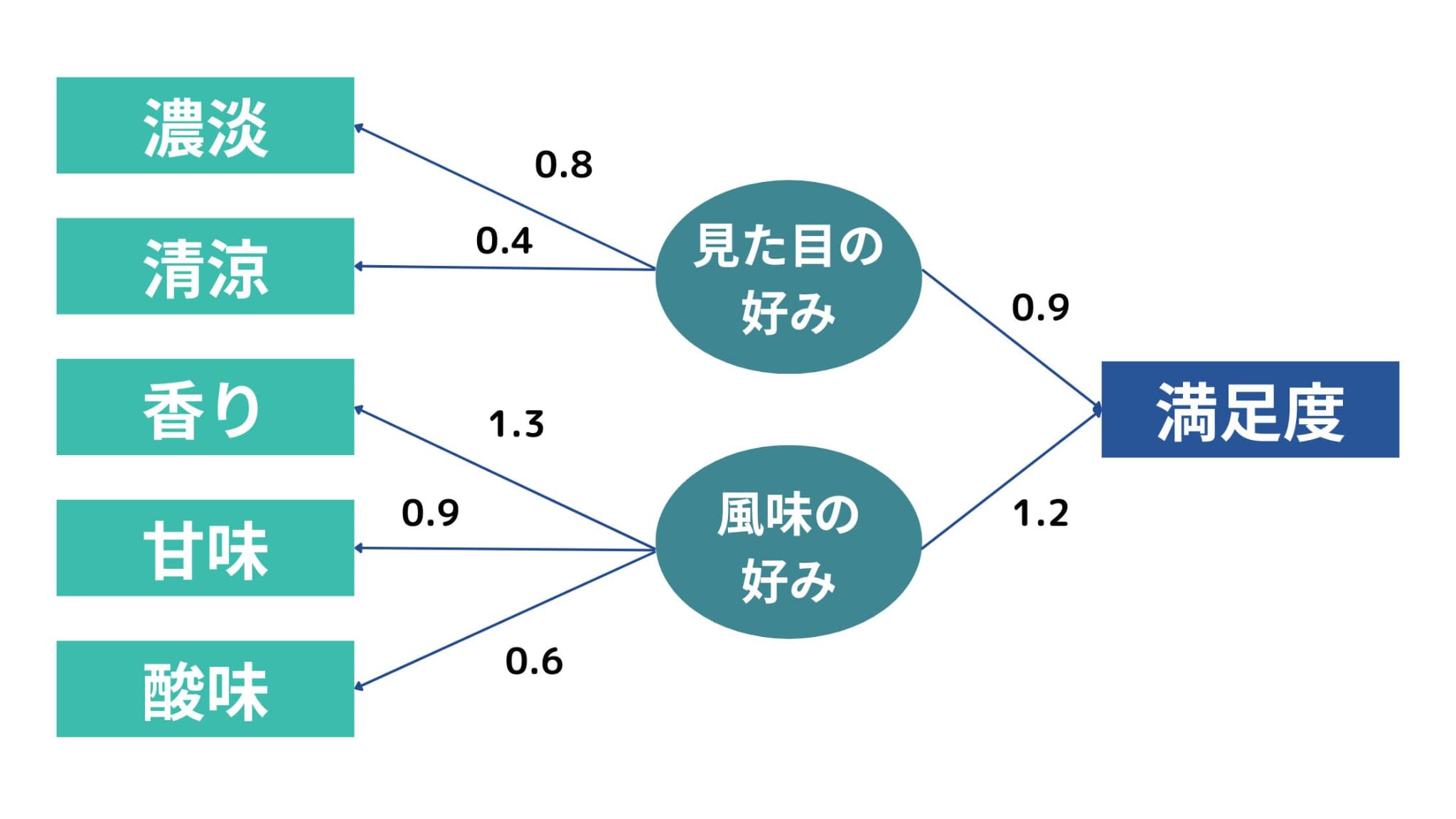
このような図が結果として得られます(イメージ)。この図をパス図と呼びます。
図にある数値は標準偏回帰係数で、因果の大きさを示しています。
このように、共分散構造分析を行うことで観測変数と潜在変数の因果関係をモデル化することができ、変数間の構造を簡単に把握することができるようになります。
そうなんです。
実は共分散構造分析とは、パス解析と因子分析の両方の機能を持つ分析手法なのです!
パス解析とは、観測変数だけを用いて因果関係をパス図としてモデル化する手法のこと。
みなさんもよく知る回帰分析の、標準偏回帰係数を因果関係の強さとみなしてモデル化します。
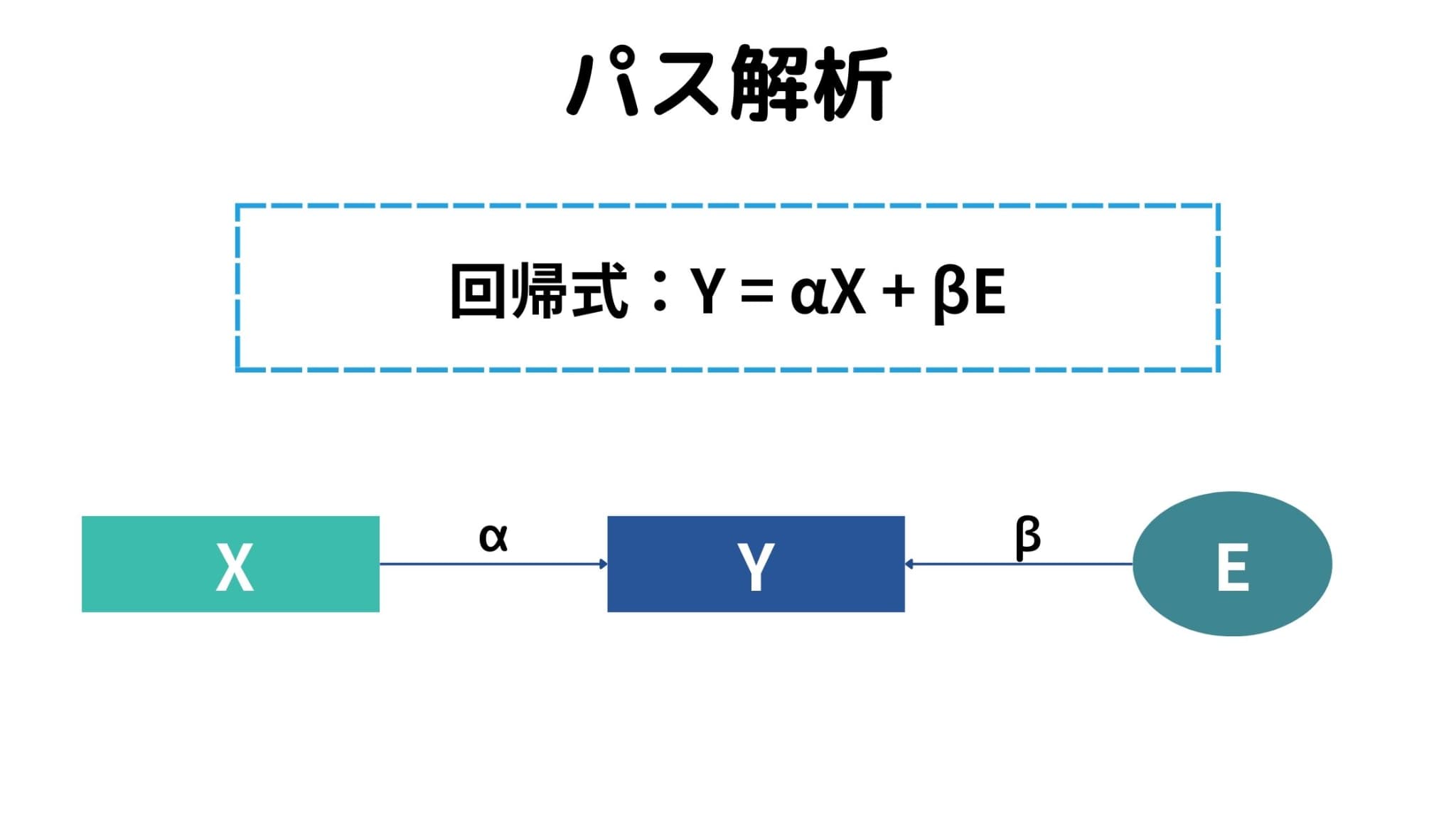
これにさらに因子分析の機能が加わることで、観測変数を潜在変数化し、上の例のように因果関係を把握することができるようになるのです。

共分散構造分析のメリット

共分散構造分析のメリットは主に2つあります。
1. データの構造がわかりやすくなる
共分散構造分析を行うことで、データの構造がわかりやすくなります。
上のワインの例で示したように、結果をパス図として出力できるので、どの変数がどの変数と関係を持つのかが一目でわかります。
2. 変数間の因果関係がわかる
共分散構造分析を行うことで、変数間の因果関係がわかります。
もう一度、先ほどのワインの例を見てみましょう。

この図を見ると、例えば、見た目の好み→満足度の値が0.9であるのに対し、風味の好み→満足度の値が1.2であることがわかります。
この値は、因果の大きさを表しています。
つまり、風味の好みの方が満足度に対してより大きな影響を与えると言えます。
同様に、風味の好みが香りの点数に対してより大きな影響を与えるということも言えますね。
このように、因果の方向を知ることができ、因果の大きさを比較できるのが共分散構分析の大きなメリットです。
共分散構造分析を行う際の注意点

共分散構造分析を行う際、注意しなければならないことが2つあります。
1. 目的変数が観測されているデータに対して適用可能
1つ目は、目的変数が観測されているデータに対して適用することが可能ということです。
因子分析と似ているため勘違いされがちですが、共分散構造分析の目的は潜在変数と観測変数の因果関係をモデル化すること。
つまり、原因から生じる結果を示す変数が必要ということです。
ここが因子分析との違いでもあり、手法の使い分けのポイントでもあるので注意しましょう。
2. 妥当な仮説の設定
2つ目は、最初に妥当な仮説を設定する必要があるということです。
上のワインのアンケートデータ例でも行っていますが、共分散構造分析では最初に仮説を立ててから構造モデルを作っていきます。
最初の段階でおかしな仮説を立ててモデルを作ってしまうと、妥当な結果が得られなくなってしまいます。
一般的な理論や他者の論文などを参考にして、妥当な仮説を立ててから分析をスタートすることを心がけましょう。
共分散構造分析の活用例

共分散構造分析はいくつかの変数が観測されているデータに対して適用することができます。
そんな中でも、よく共分散構造分析が用いられるのがアンケート結果の分析。
上のワインの例と同じように、「ある目的変数に対して、どの観測変数、潜在変数がどのくらい効果をもたらしているのか」を分析することを目的として用いられます。
さらに分析結果を活用することで、マーケティング戦略の立案なども効率的に行うことができます。
Pythonで共分散構造分析をやってみよう

ここからは、Pythonで実際に共分散構造分析をやっていきます。
分析の目的は、パス図を出力して変数間の因果関係を明らかにすること!
以下の流れで分析を進めていきます。
1. ライブラリのインストール
2. データの準備
3. 変数の標準化
4. 基礎分析(相関の確認)
5. 仮説モデルの設定
6. 共分散構造分析の実行
7. パス図の出力
1. ライブラリのインストール
今回はsemopyと呼ばれるライブラリを使用します。
また、分析で使用するモジュール等もここで全てimportしておきます。
今回はGoogle colabで実行していくため必要なライブラリを以下のように!pip installでインストールしておきます。※ターミナルから入れる場合は!を付けずにpip installしてください。
numpyやpandasなどは元からGoogle colabにインストール済みなので改めて!pip install必要はありません。
#共分散構造分析を行うためのライブラリ
!pip install semopy#パス図を出力するためのライブラリ
!pip install graphviz#モジュールのインポート
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import semopy
from semopy import Model
from sklearn import datasets2. データの準備
データはscikit-learnが提供している糖尿病患者のデータを使用します。
#糖尿病データセット
df = datasets.load_diabetes(as_frame=True).frame
df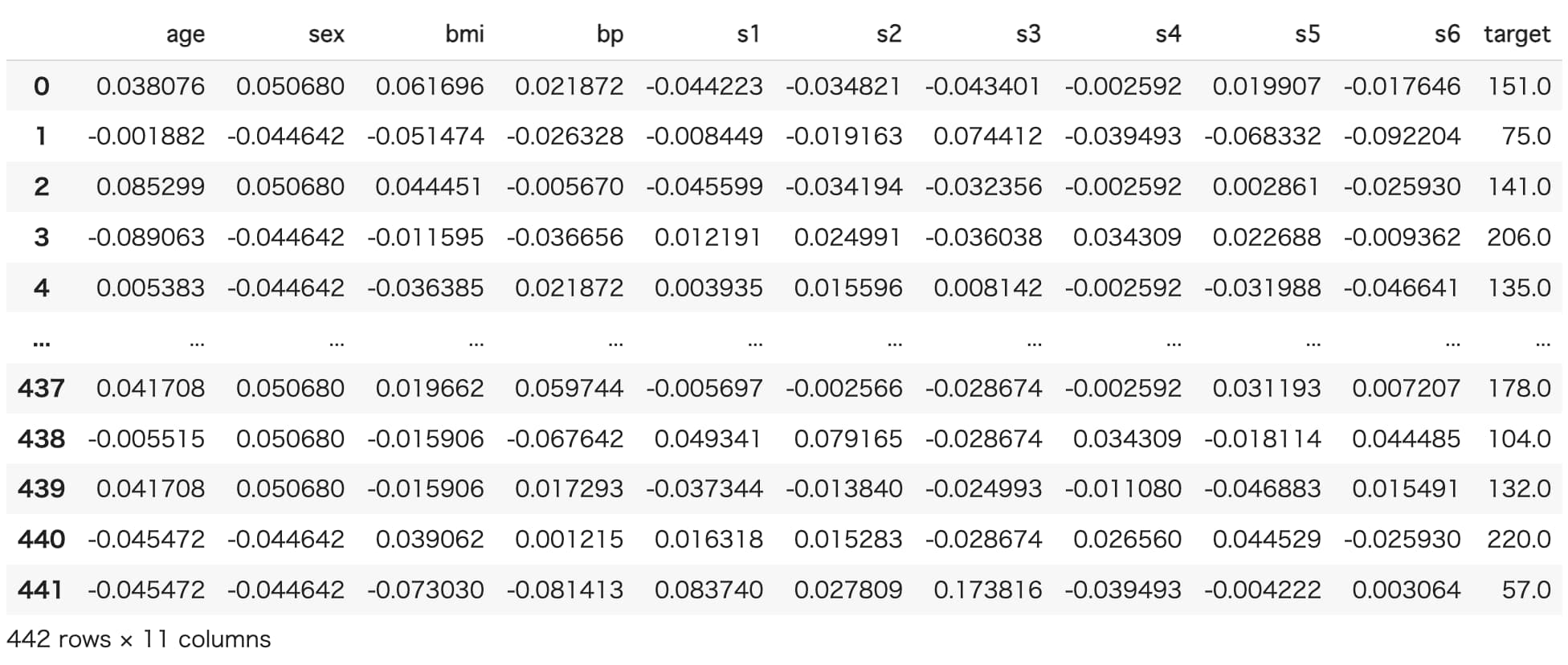
各変数の説明は以下の通りです。
age:年齢
sex:性別
bmi:BMI
bp:平均血圧
s1:TC(血液中の総コレステロール値)
s2:LDL(低比重リポタンパク質、悪玉コレステロール)
s3:HDL(高比重リポタンパク質、善玉コレステロール)
s4:TCH(=TC÷HDL=総コレステロール値/善玉コレステロール)
s5:LTG(血液中の中性脂肪値の対数)
s6:GLU(血糖値)
target:測定時から1年後の糖尿病の進行度を示す値
サンプルサイズは442です。
3. 変数の標準化
次に、各変数の単位による影響をなくすためのデータの標準化を行います。
一見すると読み込んだ時点でtarget以外の変数が標準化されていそうに見えますが、特殊な標準化がされているようなので、一般的な標準化(平均 0、分散 1)を行います。
#データの標準化
df_std = df.apply(lambda x: (x-x.mean())/x.std(), axis=0)
df_std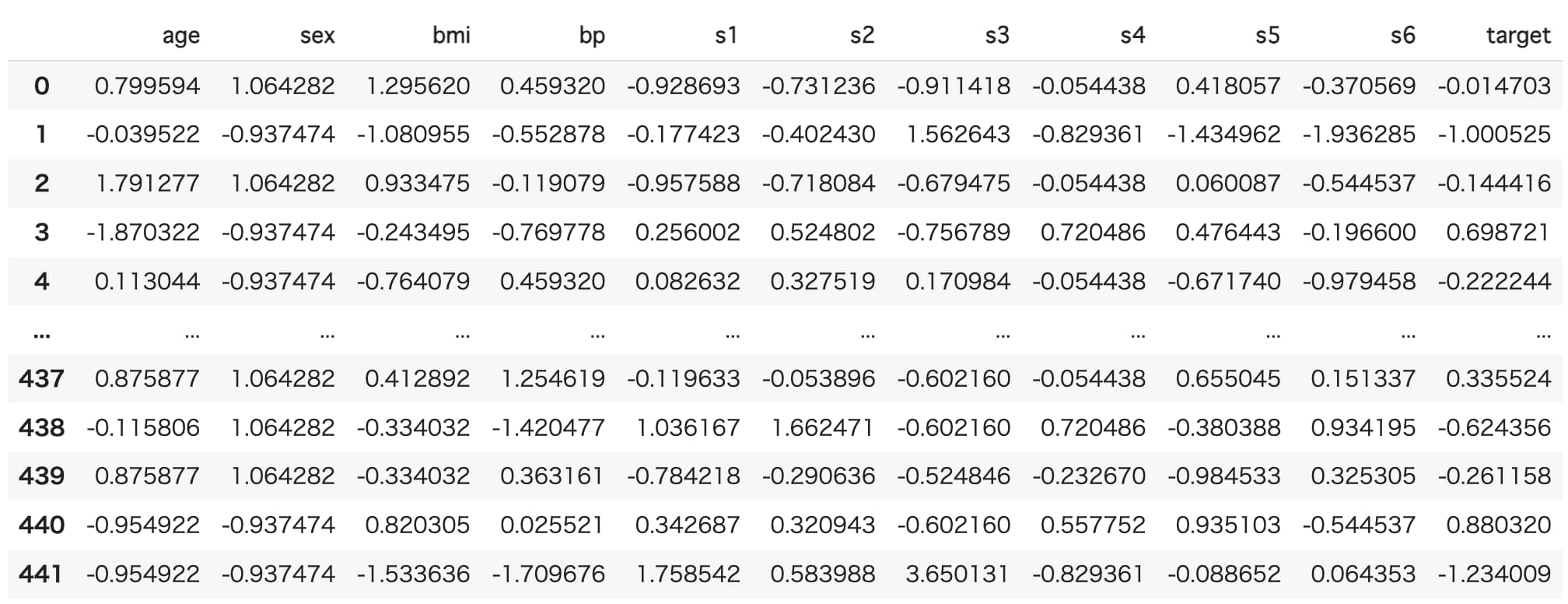
それぞれの変数が標準化されていることがわかります。
4. 基礎分析(相関の確認)
続いて、仮説を考えるための基礎分析を行います。
ここでは各変数の相関を見てみましょう。
df_std_corr = df_std.corr()
df_std_corr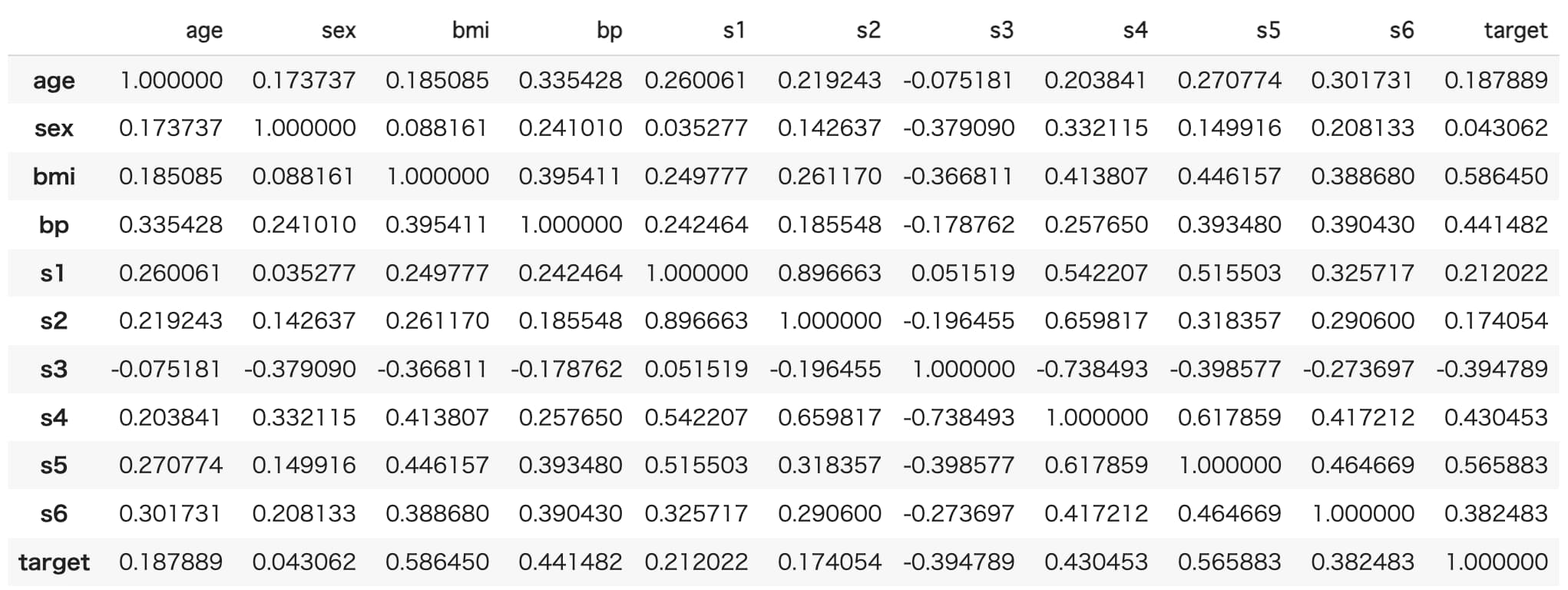
これだと少しわかりづらいので、ヒートマップを表示してみます。
sns.heatmap(df_std_corr, cmap="coolwarm", vmin=-1, vmax=1, annot=True)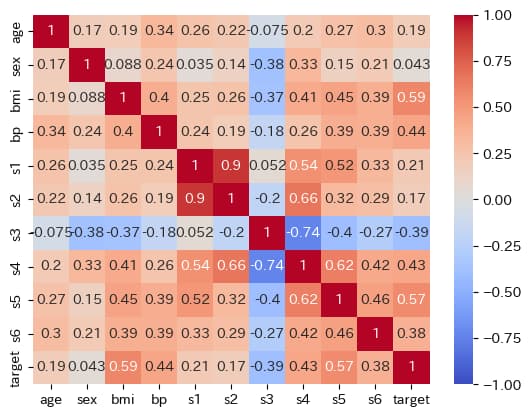
相関の大きさが色によって表現されています。
ヒートマップより、以下のことがわかります。
目的変数と最も相関が高いのはBMI、次いでs5、bp、s4
bpとBMI、s4とBMI、s4とs1、s4とs2、s4とs3、s5とBMI、s5とs1、s5とs3、s5とs4、s6とs4、s6とs5には相関あり
これをもとに、仮説を考えていきます。
5. 仮説モデルの設定
先ほどの基礎分析の結果から次のような仮説を考えました。
<仮説>
・BMI、bp、s1~s6の背後には生活習慣(LifeStyle)という潜在変数が存在
・age、sexの背後には個人情報(PersonalInfo)という潜在変数が存在
・生活習慣(LifeStyle)は個人情報(PersonalInfo)である程度説明がつく
・targetは生活習慣(LifeStyle)である程度説明がつく
・targetは個人情報(PersonalInfo)である程度説明がつく
・基礎分析の結果で見られた相関関係が観測変数間に存在する
これらの仮説をそれぞれ式(モデル)として表すと、以下のように記述することができます。
# 仮説モデルを変数descに代入する
desc = '''
# 測定方程式(潜在変数 =~ 観測変数)
LifeStyle =~ bmi + bp + s1 + s2 + s3 + s4 + s5 + s6
PersonalInfo =~ age + sex
# 構造方程式(目的変数 ~ 説明変数 、潜在or観測どちらでも良い)
LifeStyle ~ PersonalInfo
target ~ LifeStyle
target ~ PersonalInfo
# 共変関係(双方向、潜在or観測どちらでも良い)
bmi ~~ bp
bmi ~~ s4
s4 ~~ s1
s4 ~~ s3
bmi ~~ s5
s5 ~~ s1
s5 ~~ s3
s5 ~~ s4
s6 ~~ s4
s6 ~~ s5
'''これが今回立てた仮説モデルとなります。
6. 共分散構造分析の実行
さて、仮説モデルを考えることができたので、共分散構造分析を行ってみます。
5.において仮説モデルを文字型でそれぞれ入力しましたが、そのままで大丈夫です。
仮説モデルが格納された変数をModel()に代入し、学習を行っていきます。
# 学習器を用意
mod = Model(desc)
# 学習結果をresに代入する
res = mod.fit(df_std)
# 学習結果のパラメータ一覧を表示する
inspect = mod.inspect()
print(inspect)
このような形で、学習後のパラメータを確認することができます。
また、仮説モデルに基づき作成されたモデルの評価指標を見てみましょう。
# モデルの評価指標を表示
stats = semopy.calc_stats(mod)
# 転置して表示
print(stats.T)
様々な指標が表示されていますが、ここで注目したいのがCFI、GFI、AGFI、NFIの4つ。
詳しい説明は省きますが、これらはモデルの適合度指標と呼ばれ、0.95以上であれば良いモデルと言えます(詳しくはこちら)。
今回の結果では大きく下回っているため、良いモデルとは言えません。
ただし、これらの値が良くなければモデルとして全く意味をなさないというわけではありません(変数間の構造をある程度把握することは可能です)。
モデルの評価指標とパス図を確認してみて、総合的な判断を下すのが良いでしょう。
7. パス図の出力
最後に、本分析の目的であるパス図の出力を行います。
pass_graph = semopy.semplot(mod, "sample.png",plot_covs=True,engine="circo")
pass_graph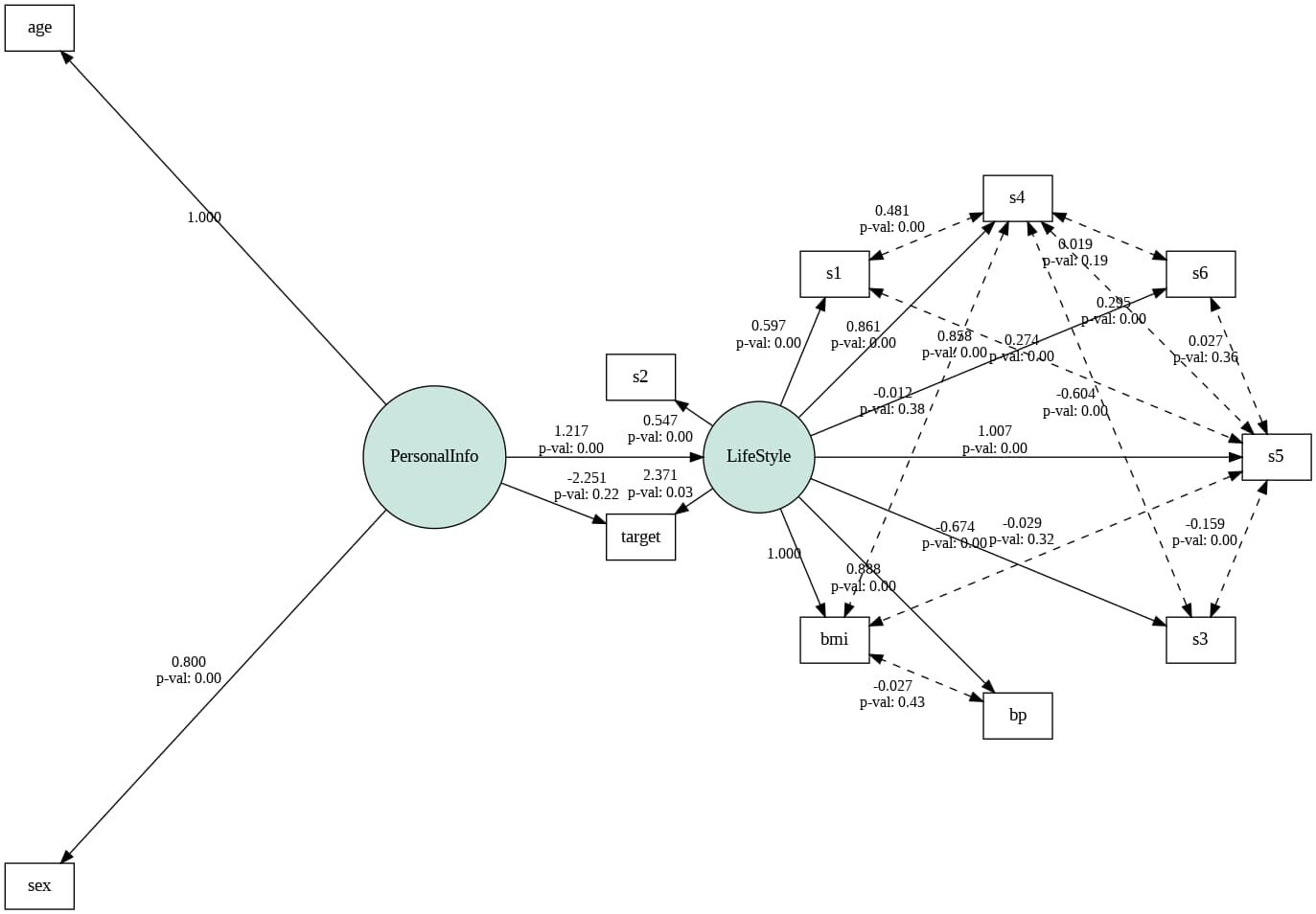
パス図には標準偏回帰係数(因果の大きさを示す値)とp-value(有意性を示す値、0.05未満なら有意)が記載されています。
出力結果より、生活習慣(LifeStyle)からtargetへの効果は2.371で、有意であることがわかります。一方で、個人情報(PersonalInfo)からtargetへの効果は-2.251で、有意ではないことがわかります。
このことから、モデルの適合度はそれほど高くはないが、BMIやbpなどの値を決める変数である生活習慣が1年後の糖尿病の進行状況に効果を及ぼすと言えます。
今回は各観測変数を2つの潜在変数にまとめるという仮説を立てましたが、他の仮説モデルを立てて同様に分析を進めると、また違った結果が得られるかもしれません。
まとめ
今回は共分散構造分析の概要からPythonでの実装方法まで解説していきました。
共分散構造分析は、ビジネスの現場においてよく用いられる手法です。
共分散構造分析を用いることで、因果関係をモデル化することができ、マーケティング戦略などへ落とし込むこともできます。
複数の変数が観測されているデータが手元にあり、何かしらの仮説が考えられる場合は積極的に共分散構造分析を行っていきましょう!
また、今回分析に用いたPythonについて勉強したい方は以下の記事を参考にしてみてください!

さらに詳しくAIやデータサイエンスの勉強がしたい!という方は当サイト「スタビジ」が提供するスタビジアカデミーというサービスで体系的に学ぶことが可能ですので是非参考にしてみてください!
AIデータサイエンス特化スクール「スタアカ」

| 【価格】 | ライトプラン:1280円/月 プレミアムプラン:149,800円 |
|---|---|
| 【オススメ度】 | |
| 【サポート体制】 | |
| 【受講形式】 | オンライン形式 |
| 【学習範囲】 | データサイエンスを網羅的に学ぶ 実践的なビジネスフレームワークを学ぶ SQLとPythonを組み合わせて実データを使った様々なワークを行う マーケティングの実行プラン策定 マーケティングとデータ分析の掛け合わせで集客マネタイズ |
データサイエンティストとしての自分の経験をふまえてエッセンスを詰め込んだのがこちらのスタビジアカデミー、略して「スタアカ」!!
当メディアが運営するスクールです。
24時間以内の質問対応と現役データサイエンティストによる複数回のメンタリングを実施します!
カリキュラム自体は、他のスクールと比較して圧倒的に良い自信があるのでぜひ受講してみてください!
他のスクールのカリキュラムはPythonでの機械学習実装だけに焦点が当たっているものが多く、実務に即した内容になっていないものが多いです。
そんな課題感に対して、実務で使うことの多いSQLや機械学習のビジネス導入プロセスの理解なども合わせて学べるボリューム満点のコースになっています!
Pythonが初めての人でも学べるようなカリキュラムにしておりますので是非チェックしてみてください!
ウォルマートのデータを使って商品の予測分析をしたり、実務で使うことの多いGoogleプロダクトのBigQueryを使って投球分析をしたり、データサイエンティストに必要なビジネス・マーケティングの基礎を学んでマーケティングプランを作ってもらったり・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践してもらったりする盛りだくさんの内容になってます!
・BigQuery上でSQL、Google Colab上でPythonを使い野球の投球分析
・世界最大手小売企業のウォルマートの実データを用いた需要予測
・ビジネス・マーケティングの基礎を学んで実際の企業を題材にしたマーケティングプランの策定
・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践して稼ぐ

























