因子分析をわかりやすく解説!主成分分析との違いやPythonでの実装方法!

こんにちは!
データサイエンティストのウマたん(@statistics1012)です!
データを分析する際、以下のような問題に直面することがあるのではないでしょうか?
そんな時に有用なのが因子分析。
「原因」を探索して理解するための手法として、マーケティングの現場でもよく用いられる手法なんです!
この記事では、そんな因子分析の特徴とPythonでの実装を見ていきたいと思います。
以下のYoutubeでも解説しているので合わせてチェックしてみてください!
目次
因子分析とは

因子分析は、心理学者が人間の心理的能力の把握を試みたことに端を発しています。
教師データ(正解データ)がいらない手法であり、手元にあるデータの背後にある共通因子を探る解析手法です。
もっと簡単に言うと、原因を探索するための解析手法。
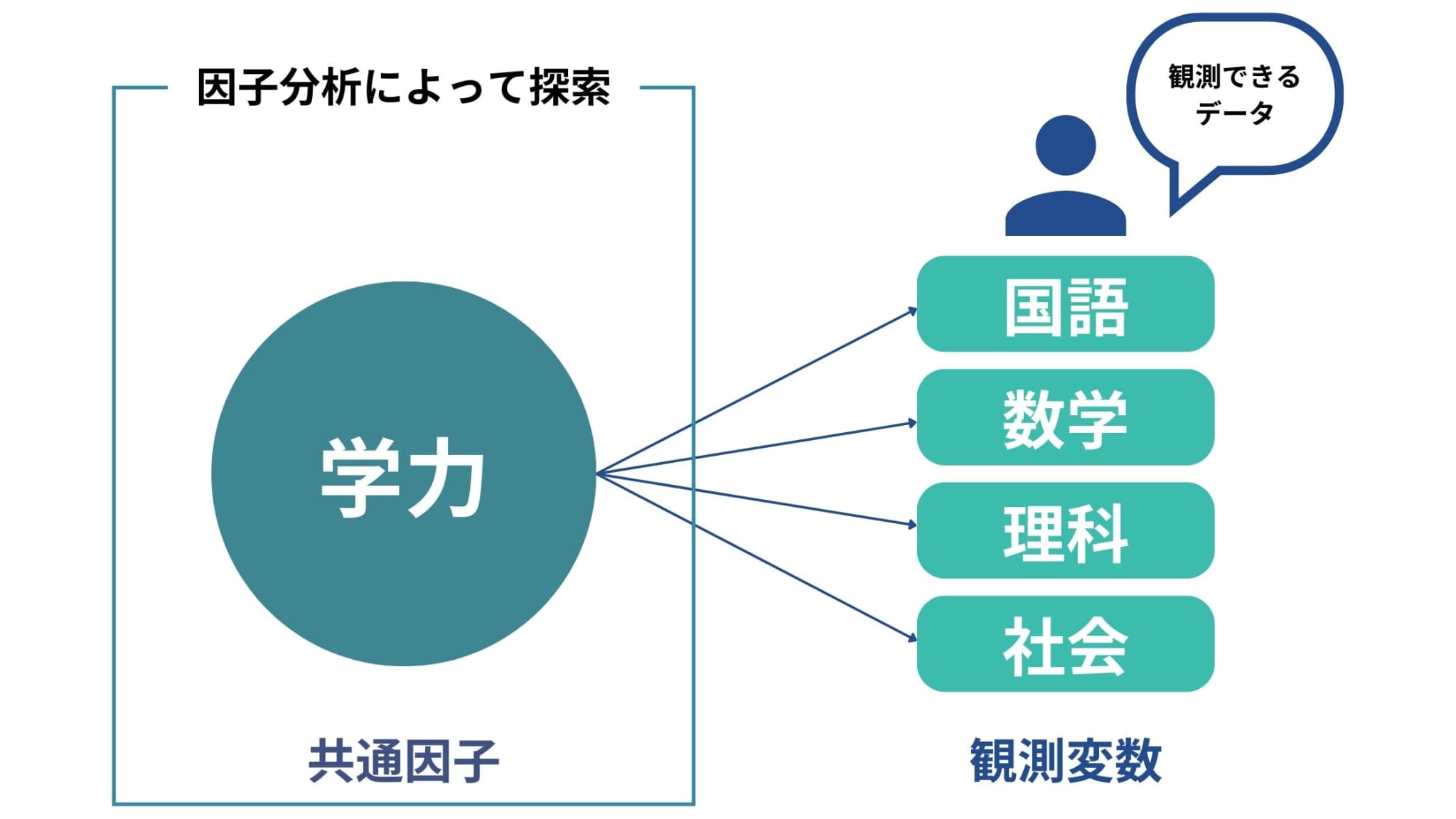
良く例として取り上げられるのが学校の成績の例。
生徒それぞれに対して国語・数学・理科・社会の点数が変数として存在する場合を考えてみましょう。
一般的に、これら4つの科目の成績の間には正の相関があると考えられます。
因子分析では、このように4つの科目間に相関があると考えられる時、「実は背後には学力という共有に作用する潜在的な因子があり、学力とそれぞれの科目に正の相関があるので、4科目間に相関が現れている」と考えます。
つまり、学力が高いから成績が良いという考え方です。
学力は直接観測することができないため、各科目の成績から学力を探索しようとしているのです。
因子分析のメリット

因子分析のメリットは主に2つあります。
1. データの構造がわかりやすくなる
因子分析を行うことで、データの構造がわかりやすくなります。
以下の図は、学校の成績データに対して因子分析を行った結果を示した図です。
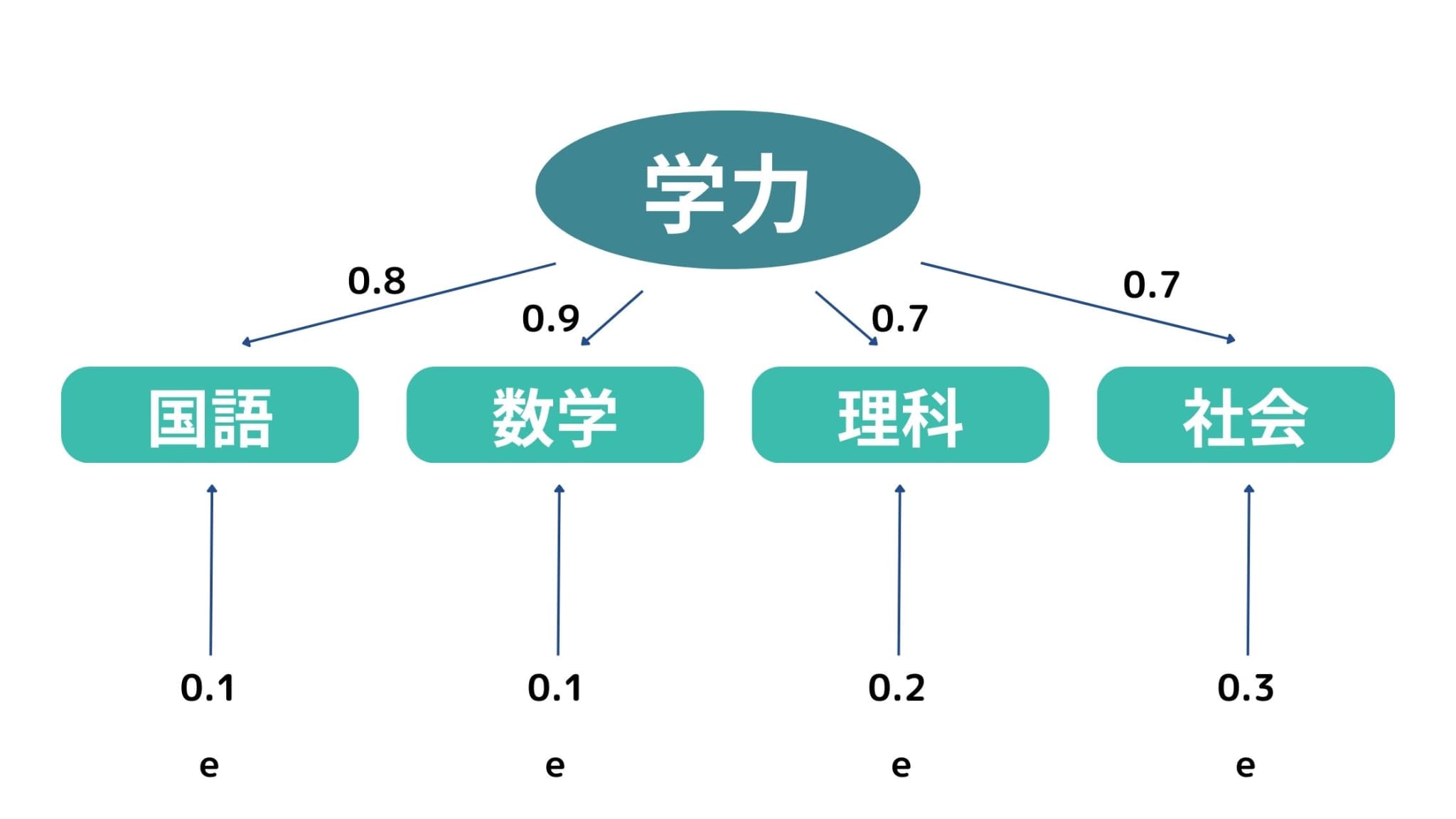
先ほどの例で、各科目の背後に存在する「学力」という共通因子を探索できると述べましたが、因子分析ではさらにどのくらい共通しているかを数値で算出することができます。
数字の絶対値が大きければ大きいほど、強く関係していると解釈することができます。
また「e」は独自因子と呼ばれ、他の変数と共通しない因子を表します。
例えば国語の点数は、「学力+独自因子」の2つの因子で構成されていることになります。
このように、因子分析によりデータの構造がわかりやすくなるのです。
2. データの解釈が容易になる
因子分析を行うことで、データを解釈しやすくなります。
先ほどと同様、学校の成績データを例に考えてみましょう。
以下のように、各生徒ごとに国語・数学・理科・社会の4つの点数が得られているとします。
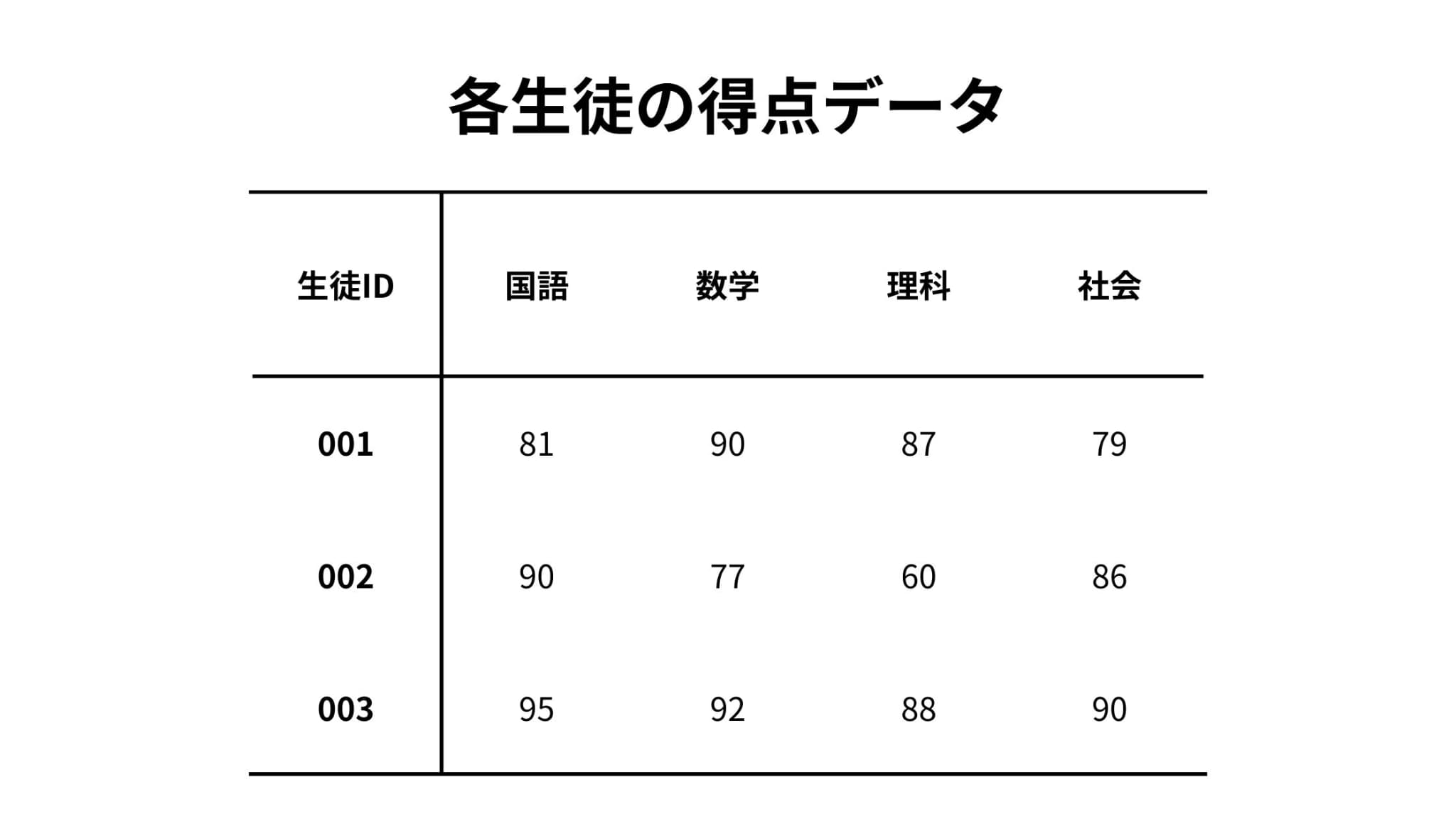
これでもある程度生徒の傾向はわかりますが、少々わかりづらい、、、。
そこでこのデータに対して因子分析を行い、共通因子である「学力」に変換すると以下のようになります。
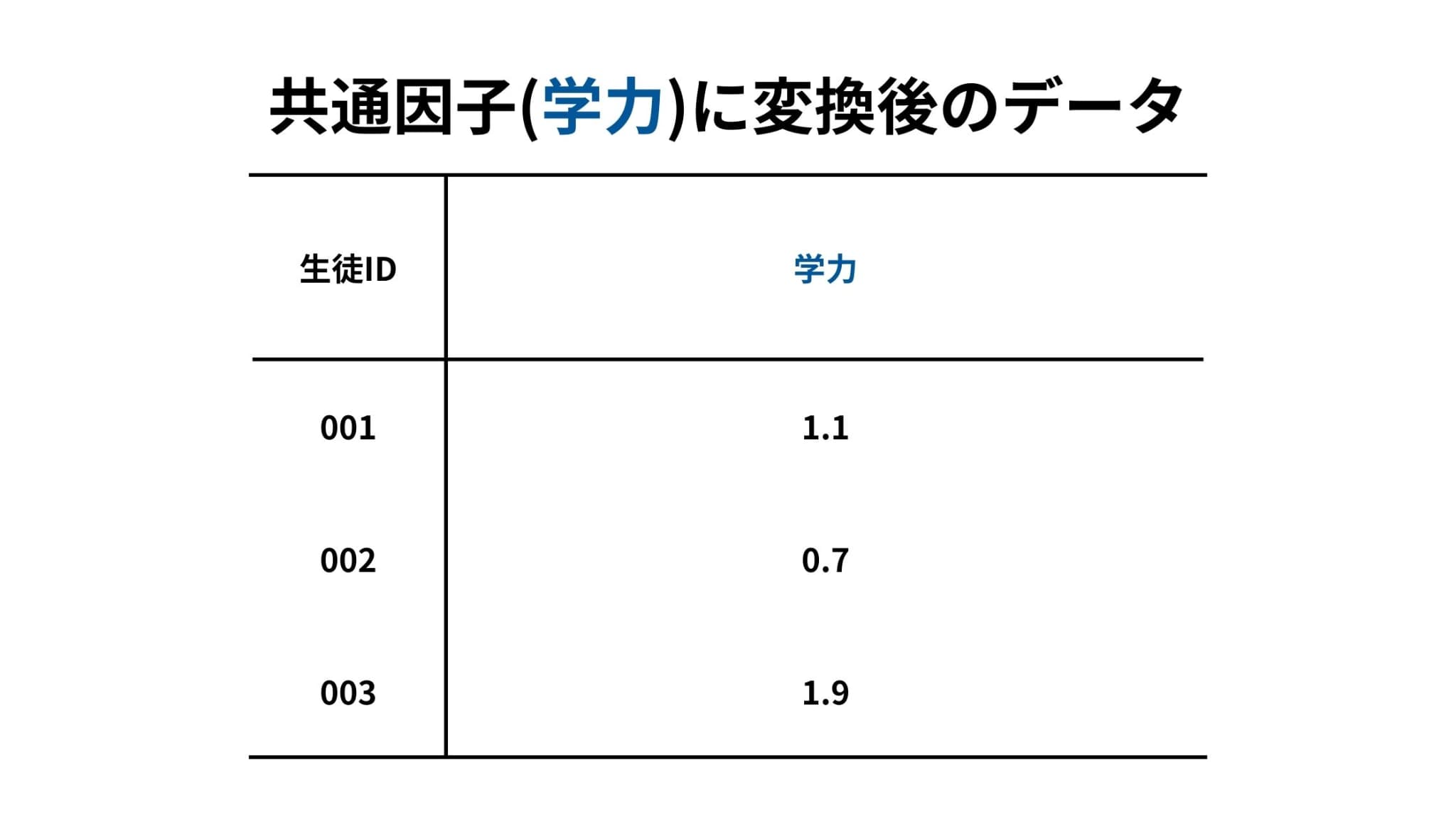
変数が1つだけとなり、各生徒の学力が一目でわかるようになりました。
また以下のように、「理系能力」と「文系能力」のような共通因子が得られることもあります。
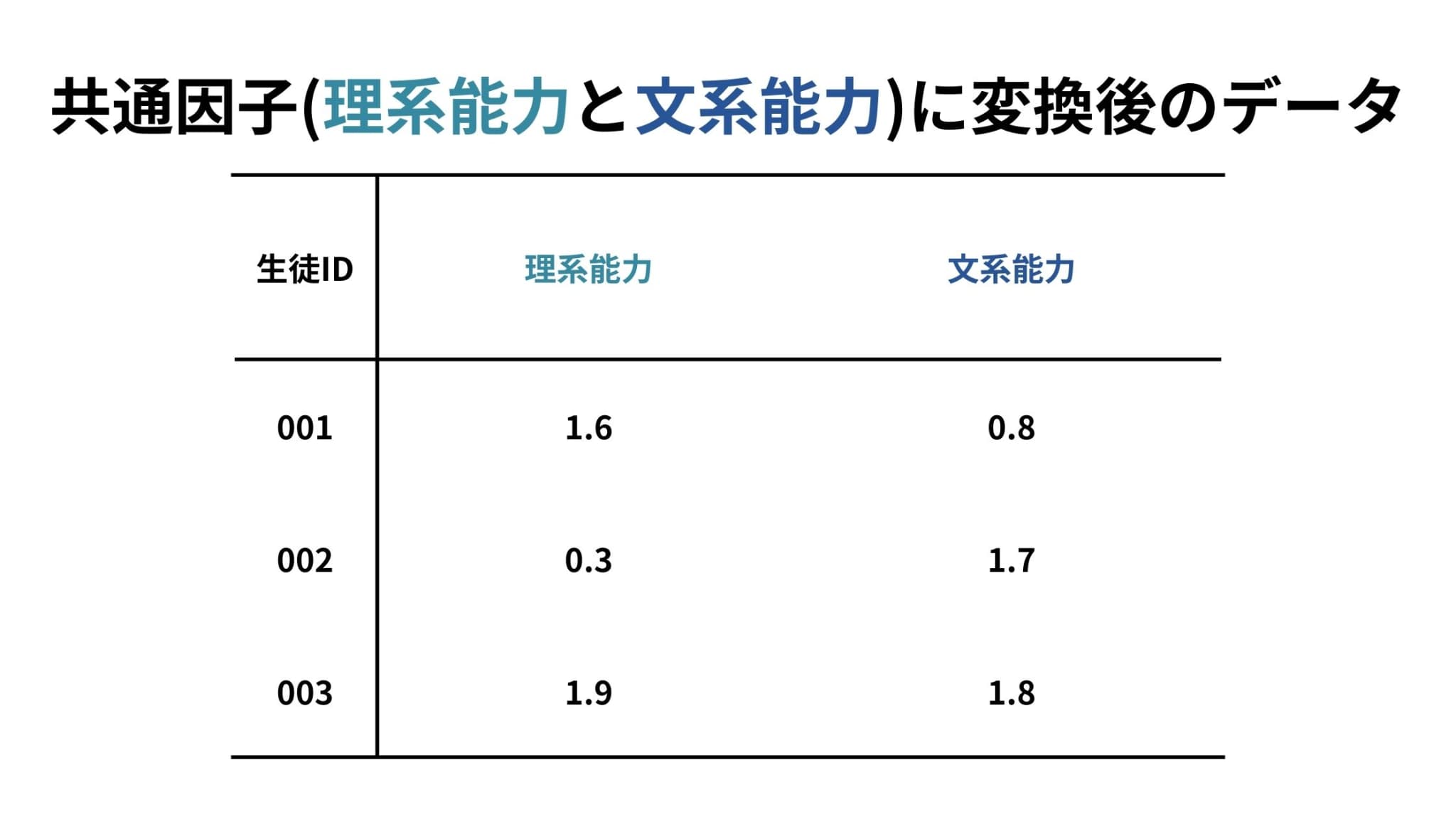
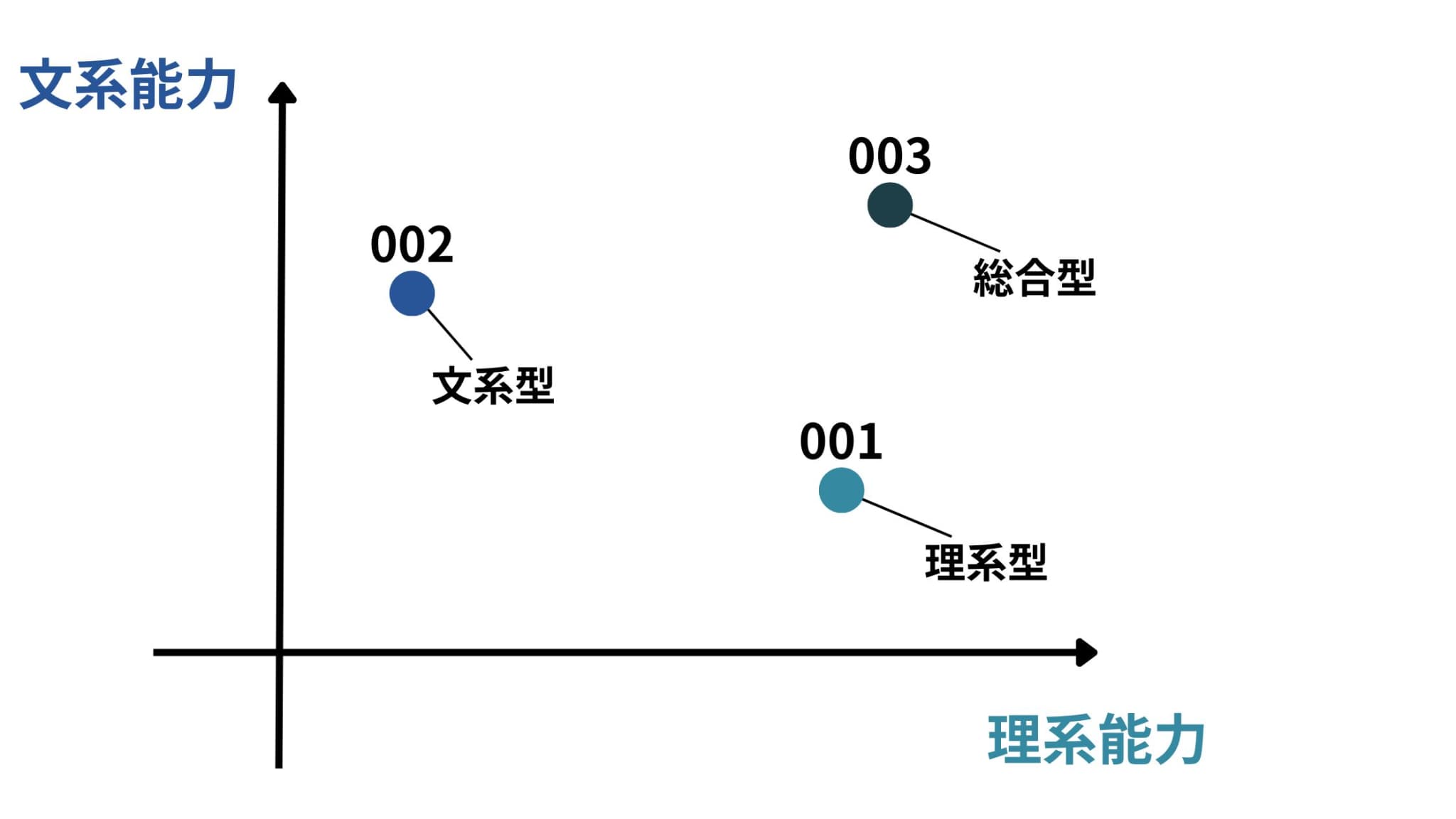
この2つの値を使えば、以下のように生徒の学力が一目でわかるグラフもすぐに作成できますね!
因子分析の活用例

因子分析はいくつかの変数が観測されているデータに対して適用することができます。
ここでは2つの活用例を紹介していきます。
1. アンケート結果の分析
よく因子分析が用いられるのがアンケート結果の分析。
主にアンケート回答者のグループ分けを目的として用いられます。
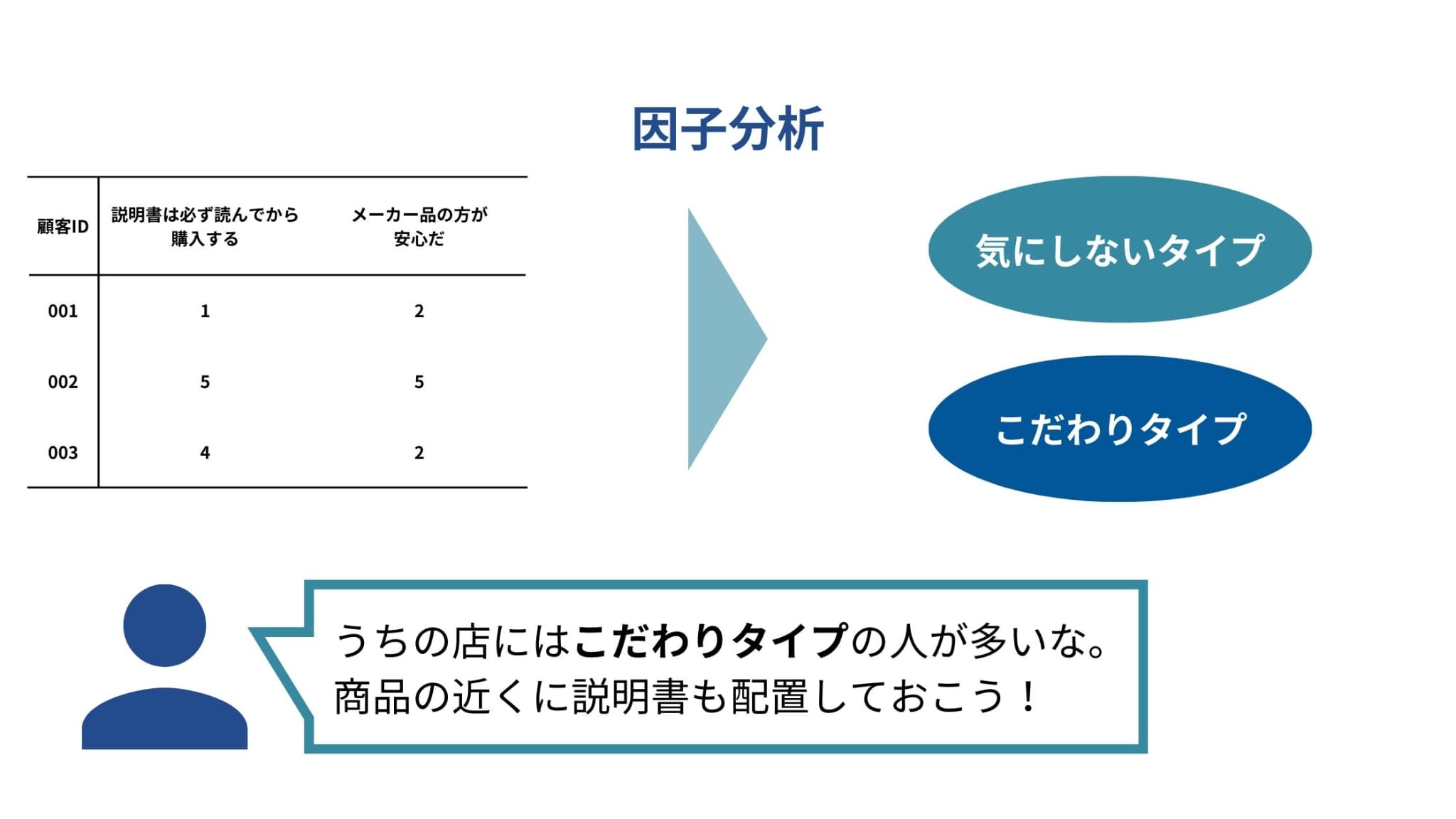
例えば、消費者の買い物行動についてのアンケートデータが手元にあるとしましょう。
「説明書は必ず読んでから購入する」、「メーカー品の方が安心だ」などの質問項目に対し、1(そう思わない)〜5(そう思う)の点数で答えるような形式です。
このデータに対して因子分析を行うことにより、消費者の購買行動に関する潜在因子を見つけ出し、それに基づいた消費者のグループ分けを行うことができます。
さらに分析結果を活用することで、マーケティング戦略の立案などを効率的に行うことができます。
2. 変数のまとめ
メリットの部分でも紹介したように、因子分析によって複数の変数をより少ない変数としてまとめることができます。
もちろん可視化のためにも重宝しますが、よく使われるのが重回帰分析との組み合わせ。
重回帰分析にそのまま説明変数を使用するのではなく、因子分析でまとめた変数を説明変数として使うことがよくあります。
これにより、モデルの解釈性の向上や多重共線性の回避が期待できます。

主成分分析との違い
ここで、よく似た分析である主成分分析との違いを説明しておきましょう!

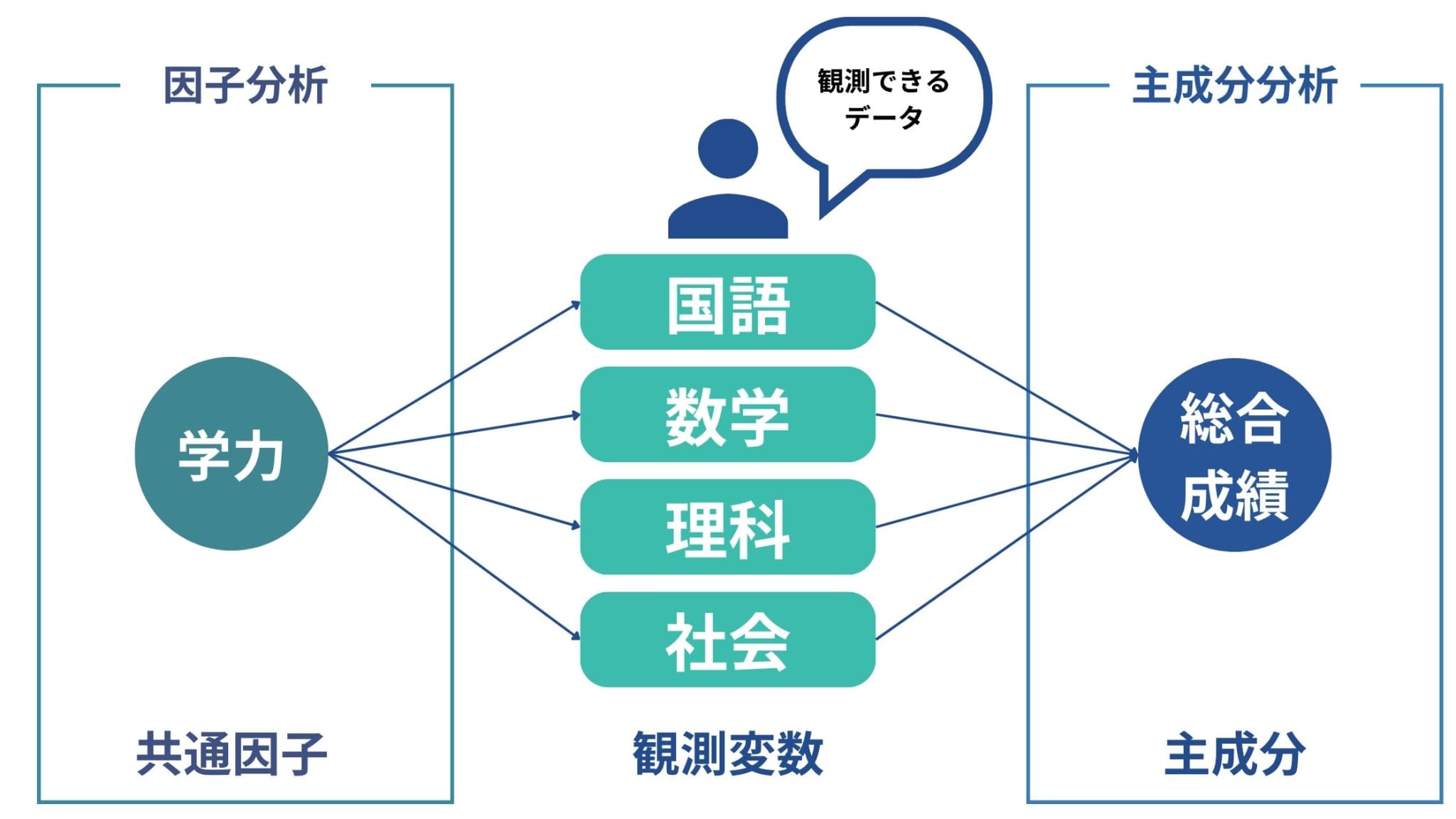
どちらも「より少ない変数にまとめる」というプロセスを辿りますが、両者の違いはズバリ分析の目的です。
因子分析が各観測変数から共通している部分を探索する分析であるのに対し、主成分分析は各観測変数をより少ない変数にまとめる分析です。
目的に合わせて分析手法を選択していきましょう!
・観測変数間の背後に存在する共通因子を見つけたい → 因子分析
・観測変数をより少ない変数にまとめたい → 主成分分析
Pythonで因子分析をやってみよう

ここからは、Pythonで実際に因子分析をやっていきます。
分析の目的は、共通因子を見つけ出すこと!
以下の流れで分析を進めていきます。
1. ライブラリのインストール
2. データの準備
3. 変数の標準化
4. 因子数の決定
5. 因子分析の実行
6. 結果の解釈
1. ライブラリのインストール
今回はfactor_analyzerと呼ばれるライブラリを使用します。
また、分析で使用するモジュール等もここで全てimportしておきます。
pip install factor_analyzerpip install japanize_matplotlib#ライブラリのインストール
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
from factor_analyzer import FactorAnalyzer2. データの準備
データはscikit-learnが提供しているワインデータを使用します。
#データの読み込み
from sklearn import datasets
wine_data = datasets.load_wine(as_frame=True).frame #ワインデータセットの読み込み
df = wine_data.drop('target',axis=1) #ワインの種類を示す変数を削除
df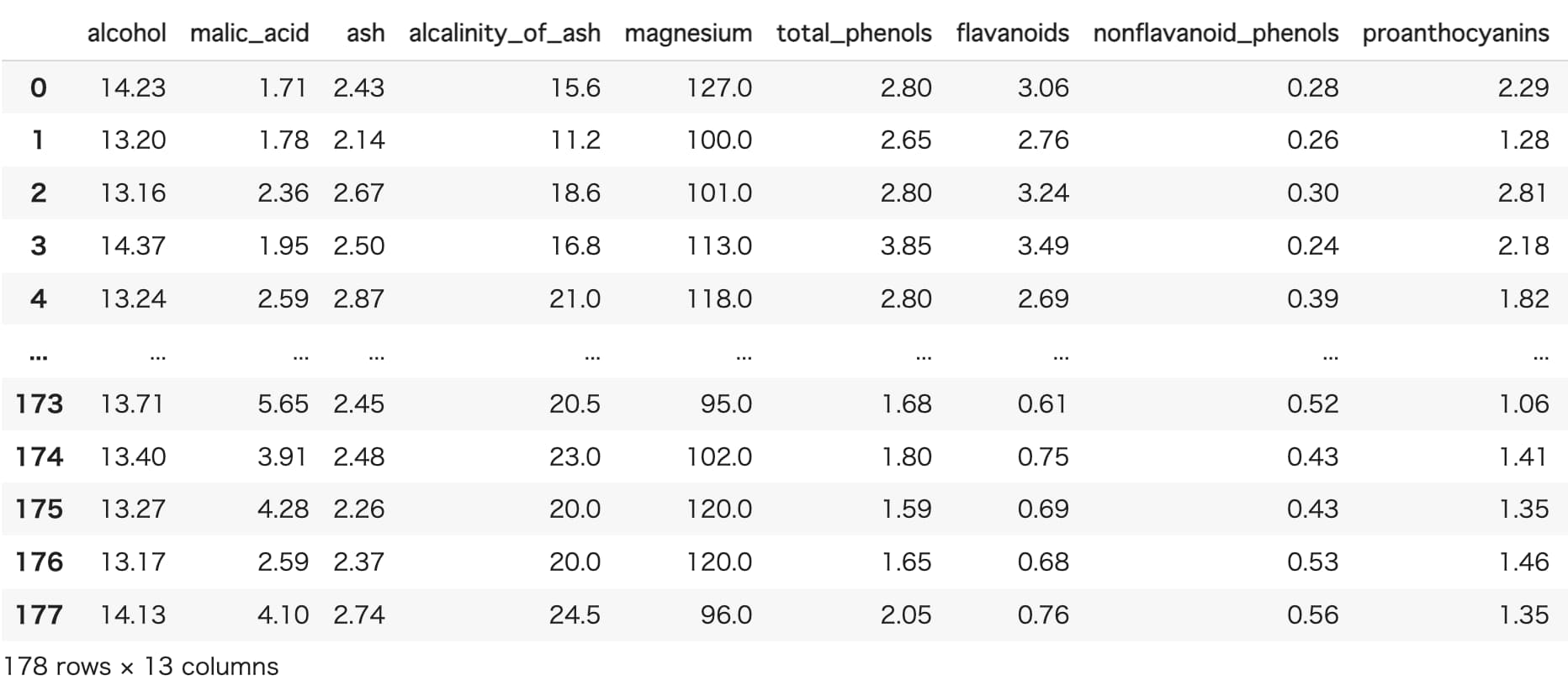
アルコール濃度やリンゴ酸濃度、ワインの種類など計14変数のデータセットとなっています。
なお今回は因子分析によって共通因子を探ることを目的としているので、ワインの種類を示す変数は削除しています。
サンプルサイズは178です。
3. 変数の標準化
次に、各変数の単位による影響をなくすためのデータの標準化を行います。
#データの標準化
df_std = df.apply(lambda x: (x-x.mean())/x.std(), axis=0)
df_std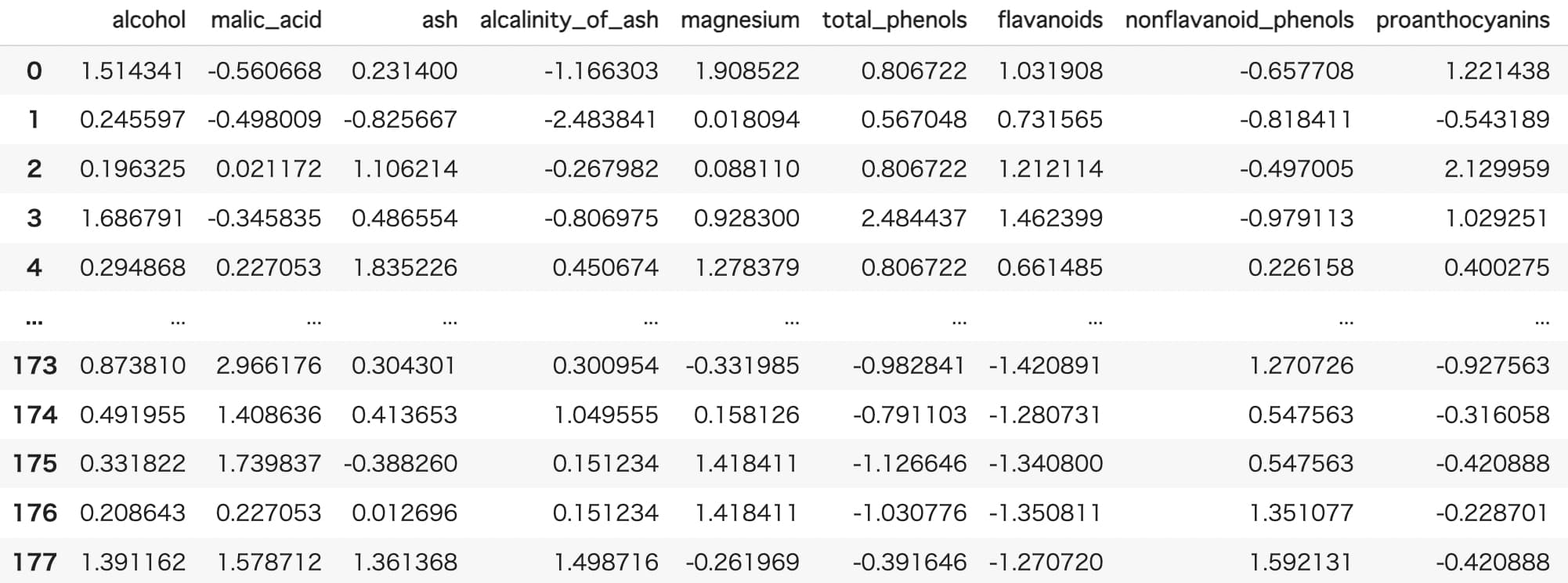
それぞれの変数が標準化されていることがわかります。
4. 因子数の決定
続いて、先ほど標準化したデータフレームの相関行列を算出し固有値を求めます。
その後、スクリープロットを描いて因子数を決定します。
#相関行列を求める
df_std_corr = df_std.corr()
#固有値を求める
ev = np.linalg.eigvals(df_std_corr)
ev_sorted = sorted(ev,reverse=True)#スクリープロットの描画
#固有値をプロット
plt.plot(ev_sorted, 's-')
# 軸名を指定
plt.xlabel("因子の数")
plt.ylabel("固有値")
plt.grid()
plt.show()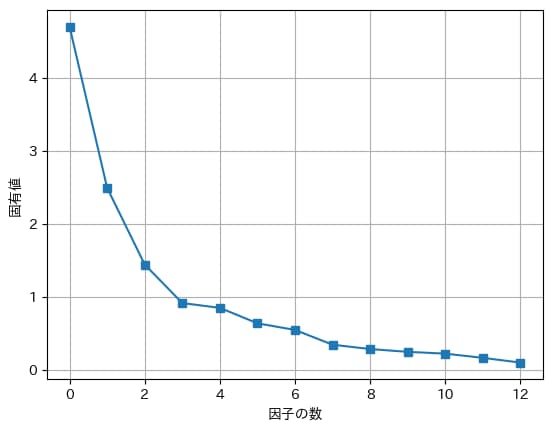
因子数の選び方には、固有値1.0以上の因子数、または固有値の累積パーセントが60%以上の因子数、またはスクリープロットが安定する因子数の3つがあります。
上のスクリープロットを見ると、3つの因子が固有値1.0以上であり、その後はスクリープロットがある程度安定していることがわかります。
よって因子数は3とします。
5. 因子分析の実行
以下のコードで因子分析を実行します。
# 因子分析の実行
fa = FactorAnalyzer(n_factors=3, rotation="promax")
fa.fit(df_std)n_factorsで因子数を指定します(今回は先ほど決定した因子数3)。
また、rotationで軸の回転方法を指定します(今回はプロマックス回転)。
6. 結果の解釈
続いて、分析結果の解釈を行います。ですがその前に、結果の見方を説明しておきましょう。
以下が分析結果になります。
# 因子負荷量,共通性の表示
loadings_df = pd.DataFrame(fa.loadings_, columns=["第1因子", "第2因子","第3因子"]) #fa.loadingsで因子負荷量を算出
loadings_df.index = df_std.columns
loadings_df["共通性"] = fa.get_communalities() #共通性の算出
loadings_df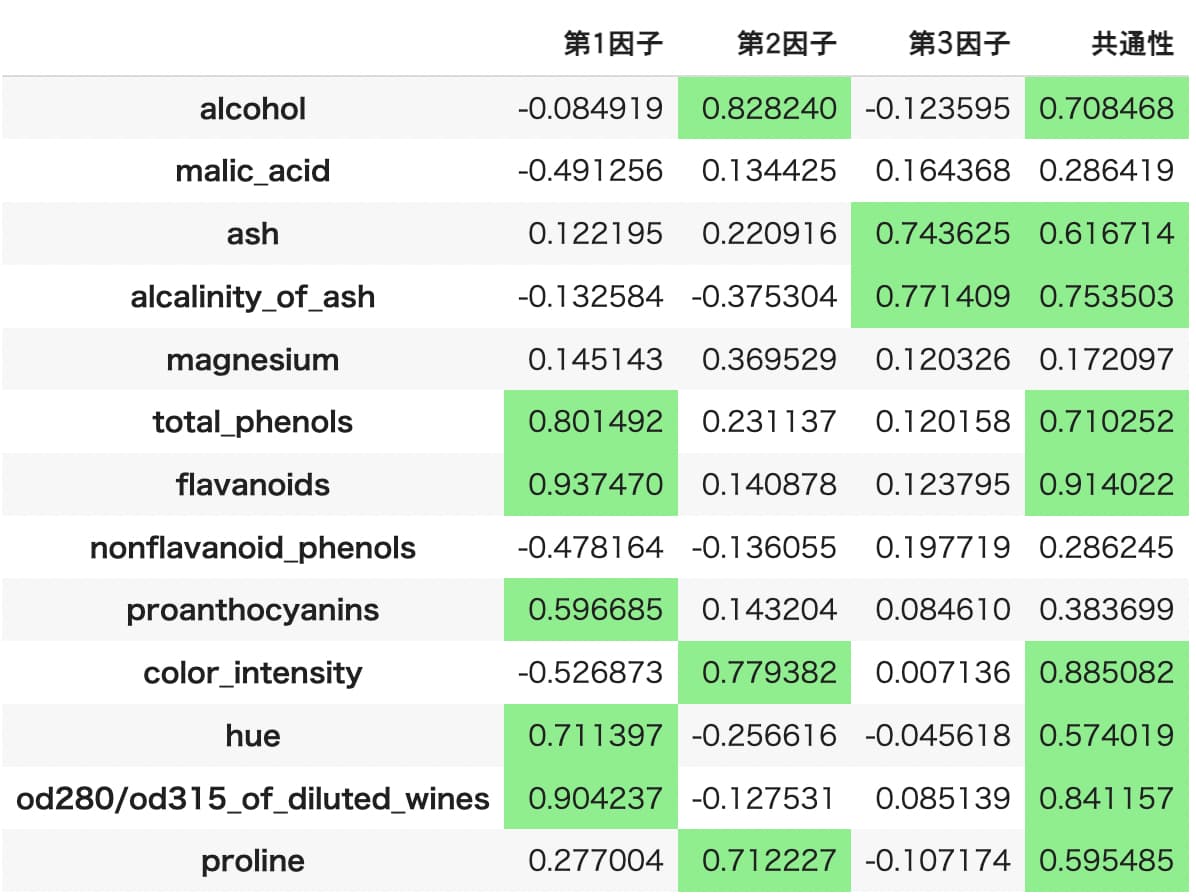
各変数ごとに因子負荷量と共通性が算出されていることがわかります。見やすくするため、値が0.5より大きい値に色付けをしてあります。
因子負荷量とは、各因子と各変数との相関係数です。つまり関係性が深い変数ほど値が大きくなり、-1から1の間の値を取ります。
共通性とは、各変数からみた因子負荷量の合計値です。つまり共通性が高いほど分析により算出された因子と深く関係していることになります。逆に、共通性が低い変数は、独自因子の割合が高いことを意味します。
さて、ここから結果の解釈に入っていきます。
因子分析の結果の解釈では、各因子に名前をつけることで解釈を行います。各変数の因子負荷量の値をもとに、因子に名前をつけていきます。
名前をつけた結果を以下に示します。
因子1:ポリフェノール量
因子2:アルコール量
因子3:ミネラル量
順番に見ていきます。
因子1:ポリフェノール量
因子1での因子負荷量が大きかったのが以下の変数。
total_phenol:フェノール量
flavanoids:フラボノイド量
proanthocyanins:プロアントシアニン量
hue:色調
od280/od315_of_diluted_wines:薄めたワインの280nmと315nmの波長の光に対する濁度
ポリフェノール類や色に関する変数がまとまっていることがわかります。
実際、赤ワインなどの色もポリフェノールが関連しているそうなので、そういった関連性をうまく一つの因子にまとめられています。
以上より、因子1をポリフェノール量と名づけました。
因子2:アルコール量
因子2での因子負荷量が大きかったのが以下の変数。
alcohol:アルコール濃度
color intensity:色の強度
proline:プロリン量
アルコール濃度、色、プロリン(アミノ酸の一種)の3つの変数がまとまっています。
各変数の関連性がわからなかったので、最も因子負荷量の大きいアルコール濃度より、因子2をアルコール量と名づけました。
因子3:ミネラル量
因子3での因子負荷量が大きかったのが以下の変数。
ash:灰分濃度
alcalinity of ash:灰のアルカリ性
灰分(ミネラル)に関する変数がまとまっていますね。
以上より、因子3をミネラル量と名づけました。
因子分析の結果、観測されたワインに関する13個の変数には3つの共通因子(ポリフェノール量、アルコール量、ミネラル量)があることがわかりました!
まとめ
今回は因子分析の概要からPythonでの実装方法まで解説していきました。
因子分析は、ビジネスの現場においてよく用いられる手法です。
因子分析を用いてデータの背後に存在する共通因子を見つけることで、問題の根本的対策を考えることができます。
複数の変数が観測されているデータがあれば、積極的に因子分析を行っていきましょう!
また、今回分析に用いたPythonについて勉強したい方は以下の記事を参考にしてみてください!

さらに詳しくAIやデータサイエンスの勉強がしたい!という方は当サイト「スタビジ」が提供するスタビジアカデミーというサービスで体系的に学ぶことが可能ですので是非参考にしてみてください!
AIデータサイエンス特化スクール「スタアカ」

| 【価格】 | ライトプラン:1280円/月 プレミアムプラン:149,800円 |
|---|---|
| 【オススメ度】 | |
| 【サポート体制】 | |
| 【受講形式】 | オンライン形式 |
| 【学習範囲】 | データサイエンスを網羅的に学ぶ 実践的なビジネスフレームワークを学ぶ SQLとPythonを組み合わせて実データを使った様々なワークを行う マーケティングの実行プラン策定 マーケティングとデータ分析の掛け合わせで集客マネタイズ |
データサイエンティストとしての自分の経験をふまえてエッセンスを詰め込んだのがこちらのスタビジアカデミー、略して「スタアカ」!!
当メディアが運営するスクールです。
24時間以内の質問対応と現役データサイエンティストによる複数回のメンタリングを実施します!
カリキュラム自体は、他のスクールと比較して圧倒的に良い自信があるのでぜひ受講してみてください!
他のスクールのカリキュラムはPythonでの機械学習実装だけに焦点が当たっているものが多く、実務に即した内容になっていないものが多いです。
そんな課題感に対して、実務で使うことの多いSQLや機械学習のビジネス導入プロセスの理解なども合わせて学べるボリューム満点のコースになっています!
Pythonが初めての人でも学べるようなカリキュラムにしておりますので是非チェックしてみてください!
ウォルマートのデータを使って商品の予測分析をしたり、実務で使うことの多いGoogleプロダクトのBigQueryを使って投球分析をしたり、データサイエンティストに必要なビジネス・マーケティングの基礎を学んでマーケティングプランを作ってもらったり・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践してもらったりする盛りだくさんの内容になってます!
・BigQuery上でSQL、Google Colab上でPythonを使い野球の投球分析
・世界最大手小売企業のウォルマートの実データを用いた需要予測
・ビジネス・マーケティングの基礎を学んで実際の企業を題材にしたマーケティングプランの策定
・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践して稼ぐ

























