こんにちは！
データサイエンティストのウマたん（@statistics1012）です。
統計学の分野で、記述統計学→推計統計学→単変量解析と来て、続いて応用的に登場するのが多変量解析！
複数の変数が存在するデータの構造を把握しパターンを見出すことに秀でた手法です。
多変量解析は、昔から存在する手法であっても現在も実務で使われているケースが多いです。
多変量解析をマスターしておくことで必ず実務の場面で役立ちます。
ということで、この記事ではそんな多変量解析について見ていきたいと思います！
目次
多変量解析とは
まずは、多変量解析とはどのような手法群なのか詳しく見ていきましょう！
以下のYoutube動画でも詳しく解説していますよ！
多変量解析とは、その名の通り「複数の変数を持った手元のデータを解析して何かしらの知見を得ること」。
よくマーケティングの文脈で用いられるのが、売れる商品の傾向を多変量解析で見ていった時に「おむつとビールの売上に相関があった」と。
これによりビールとおむつを近くに置くことで売上がアップしたそうな。
※ウォルマートの例で、本当の話なのかは紆余曲折あります
このように大量にある商品の売上の相関を調べることで、新たな傾向を見つけることができました。
この手の分析はアソシエーション分析と呼ばれ、回帰分析を行う前手に使われることが多いです。
このように統計学に端を発する多変量解析では、既存の大量データの構造を分析して何かしらの特徴を得ることを最終ゴールとします。
実は、その部分が機械学習と違う部分。
機械学習は現状のデータ構造の把握よりもとにかく未知データの予測精度を上げることを最終ゴールとすることが多いです。
機械学習と統計学の違いについては以下の記事で詳しくまとめています！
多変量解析の種類とRでの実装
続いて多変量解析にはどんな種類があるのか見ていきましょう！
適宜Rでの実装もあわせておこなっていきますよー！
重回帰分析
多変量解析の中でまず初めに覚えておいてほしい手法が、重回帰分析。
回帰分析とは「ある変数を用いて他の変数を説明（予測）するモデルを作ること」です。
土地の価格を築年数や駅からの距離や広さなどの変数で説明するみたいなモデルがよくカリキュラムに出てきますねー！
n個のサンプルがあるデータセットで一つの目的変数をp個の説明変数で説明するモデルを作ると以下のようになります。
$$y_i=\beta_0+\beta_1x_{i1}+\cdots+\beta_px_{ip}+\epsilon_i, \epsilon_i \sim N(0,\sigma^2),(i=1,\cdots,n)$$
\(y\)：目的変数、\(\beta_0\)：ある定数、\(\beta_j\)：ある係数、\(\epsilon\)：誤差項を表しています。また添え字のiはサンプルを表します。
重回帰分析は全ての手法の原点であり、絶対に抑えて欲しい手法です。
重回帰分析についてはRでの実装方法含め以下の記事で詳しくまとめていますのでチェックしてみてください！
主成分分析
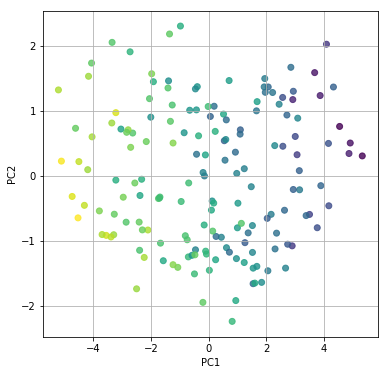
主成分分析は、1900年代前半にピアソンやホテリングにより導かれた手法であり長い歴史を持っています。
教師データ（正解データ）がいらない手法であり、手元にあるデータの次元を圧縮し構造化するのに優れています。
良く主成分分析の例として取り上げられるのが学校の成績の例。
生徒それぞれに対して算数・国語・理科・社会の点数が変数として存在します。
そんなデータセットに対して主成分分析をかけると、見事に2つの変数に集約することができます。
算数と理科は理系の能力、国語と社会は文系の能力。元々4つあった変数を2つの理系・文系という能力に集約することができるのです。
データの構造を分かりやすくすることが可能です。
変数が多くデータの構造が分かりにくい時は、主成分分析をかけてみると良いでしょう。
主成分分析については以下の記事で詳しくまとめています！
コレスポンデンス分析
多変量解析手法の1つでありアンケート調査の可視化などに使われる「コレスポンデンス分析」
コレスポンデンス分析は、データの可視化に非常に優れた手法であり、マーケティングの場でよく使われます。
それでは、早速コレスポンデンス分析をRで実装してみます。
使用するデータは、統計科学研究所の「成績データ」。以下のURLからダウンロードできます。
https://statistics.co.jp/reference/statistical_data/statistical_data.htm
| kokugo | shakai | sugaku | rika | ongaku | bijutu | taiiku | gika | eigo |
| 30 | 43 | 51 | 63 | 60 | 66 | 37 | 44 | 20 |
| 39 | 21 | 49 | 56 | 70 | 72 | 56 | 63 | 16 |
| 29 | 30 | 23 | 57 | 69 | 76 | 33 | 54 | 6 |
| 95 | 87 | 77 | 100 | 77 | 82 | 78 | 96 | 87 |
| 70 | 71 | 78 | 67 | 72 | 82 | 46 | 63 | 44 |
| 67 | 53 | 56 | 61 | 61 | 76 | 70 | 66 | 40 |
| 29 | 26 | 44 | 52 | 37 | 68 | 33 | 43 | 13 |
9科目の点数が166人分入ってます。
166人から30人抽出してコレスポンデンス分析にかけてみます。
コレスポンデンス分析はMASSパッケージのcorrepという関数で行うことが可能です。
コードは以下のように非常に簡単に実装が可能なんです。
最後の行で、結果をプロットしています。
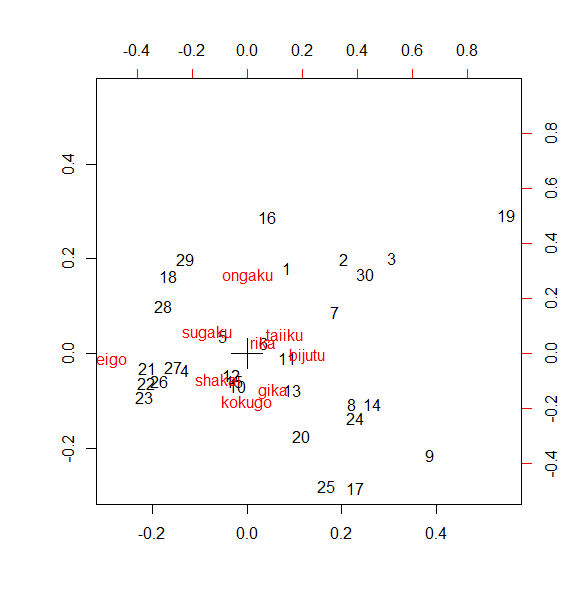
音楽と英語が他の科目と少し離れていることが分かります。
これにより、科目同士の近さや生徒の強い科目などが可視化することができました。
コレスポンデンス分析については以下の記事で詳しくまとめています！
コンジョイント分析
消費者にとって、商品のどんな機能が響くのか知りたい場合に用いられる「コンジョイント分析」
直接的に機能の良し悪しを聞くのではなく様々なスペックの商品に点数を付けてもらうことにより機能の効用値を算出するのがコンジョイント分析になります。
コンジョイント分析を行うことで、消費者にとって最適なスペックを把握することができます。
それでは、コンジョイント分析をRで実装していきましょう！
パッケージ「conjoint」を用います。
teaというデータセットに入っている、プロファイルデータを使ってコンジョイント分析を行います。
tprofは以下のようなプロファイルデータ。
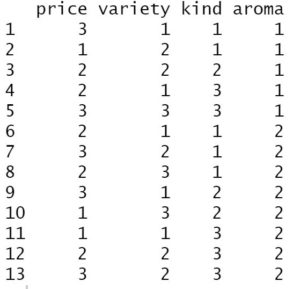
tlevnにはそれぞれの水準データが入っています。
分かりにくいのですが、この商品プロファイルは3水準×3水準×3水準×2水準になっており、priceの水準が「low/medium/high」、varietyの水準が「black/green/red」、kindの水準が「bags/granulated/leafty」、aromaの水準が「yes/no」。
最後にそれらに対する効用値が100人分入ったデータがtprefm。
これらのデータをコンジョイント分析にかけると、自動的にグラフをプロットしてくれます。
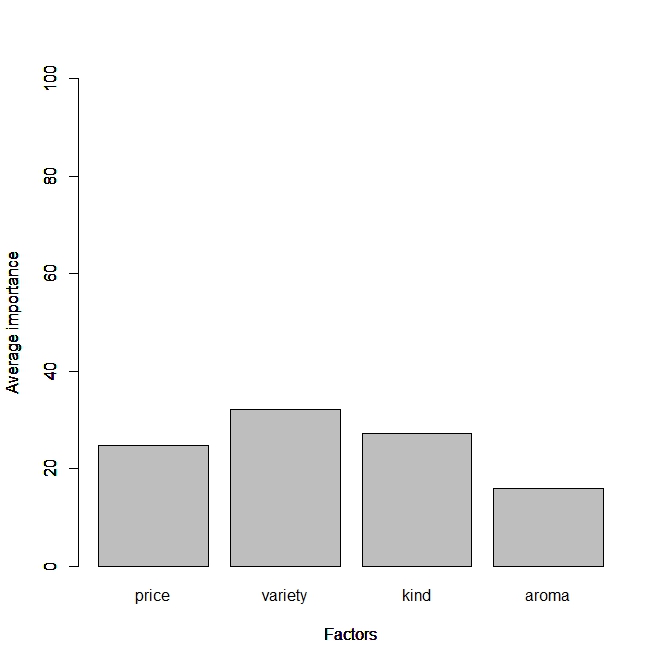
これにより要因ごとの寄与率が分かります。varietyの寄与率が若干高いですねー。
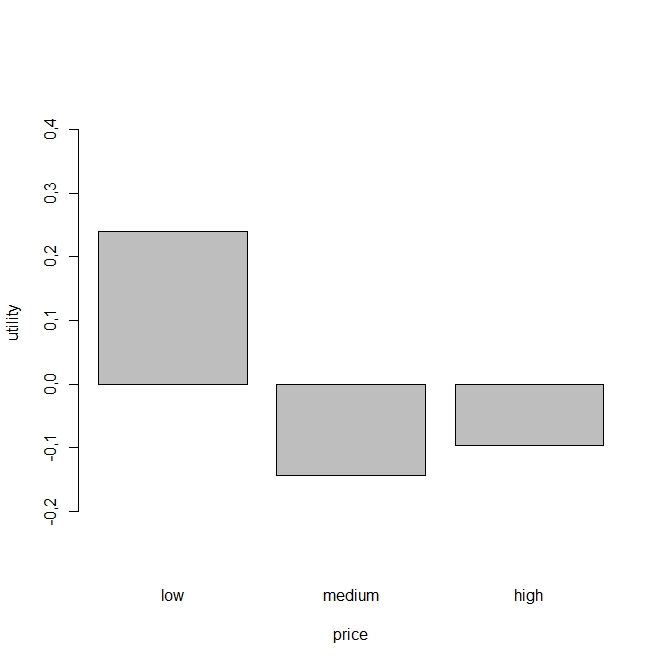
価格の部分効用値が分かります。
コンジョイント分析については以下の記事で詳しくまとめています！
階層的クラスター分析
教師なし学習の定番として取り上げられるクラスター分析！
手元のデータの特徴を基に、ある規則によってグループ分けします。
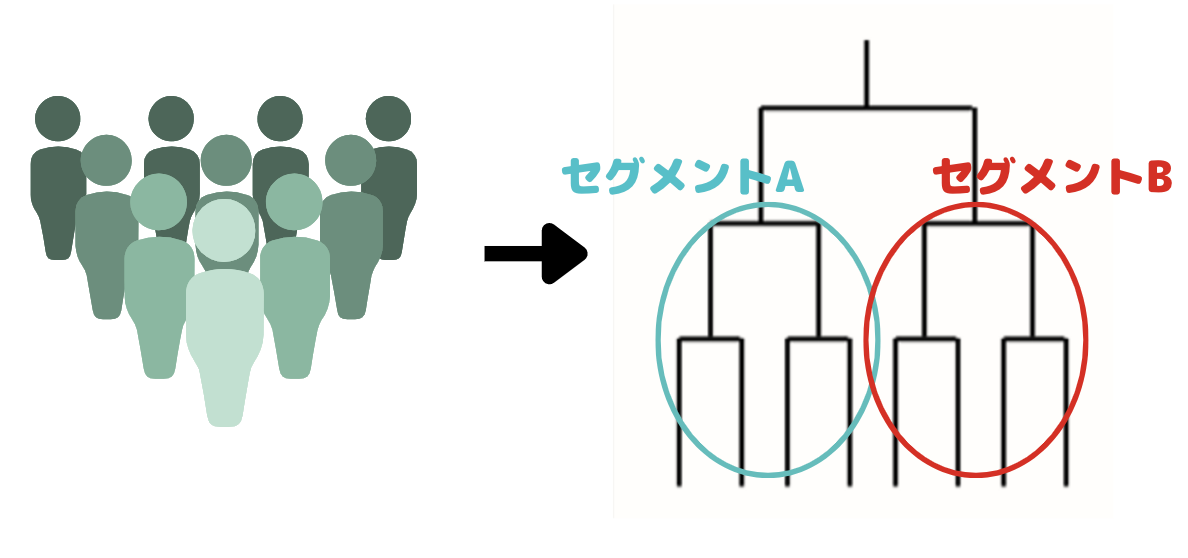
クラスター分析には階層的なタイプと非階層的なタイプがあり、階層的なタイプの方がどのようにグループ分けされたかが可視化され分かりやすくなっています。
一方、大規模データでは非階層的クラスター分析の方が計算負荷が低いため、実データでは専ら非階層的クラスター分析が使われるのが一般的です
クラスター分析については以下の記事でまとめています！
k-means
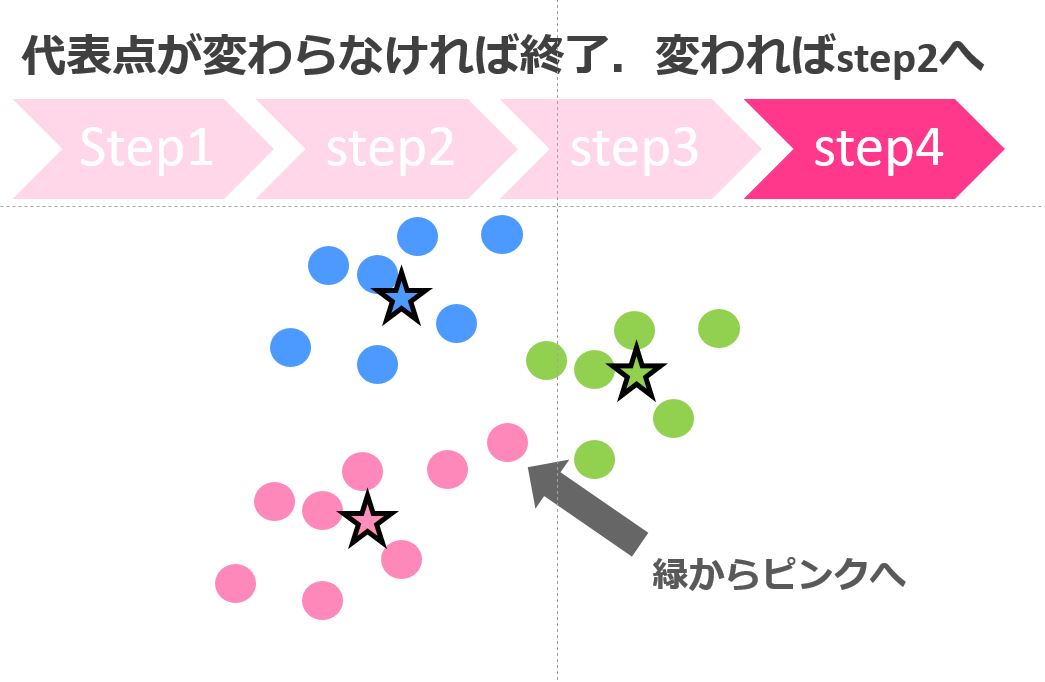
k-means法はまさに非階層のクラスター分析！
一般的にビジネスの場では膨大なデータを扱うことが多いため非階層的クラスター分析が良く用いられます。
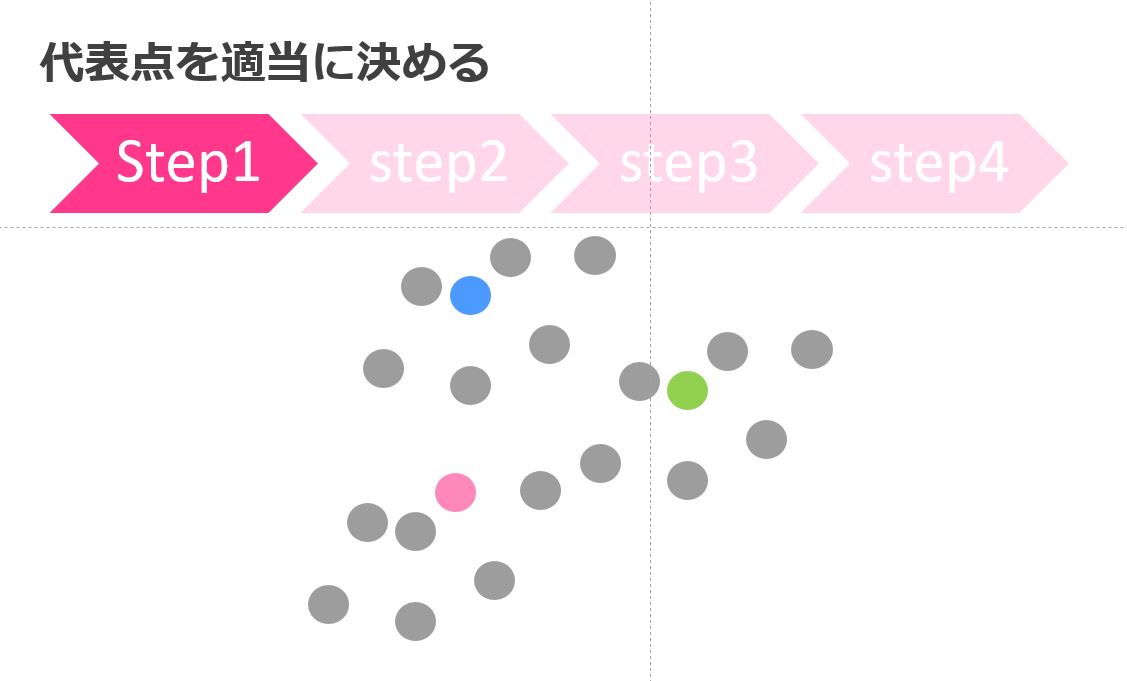
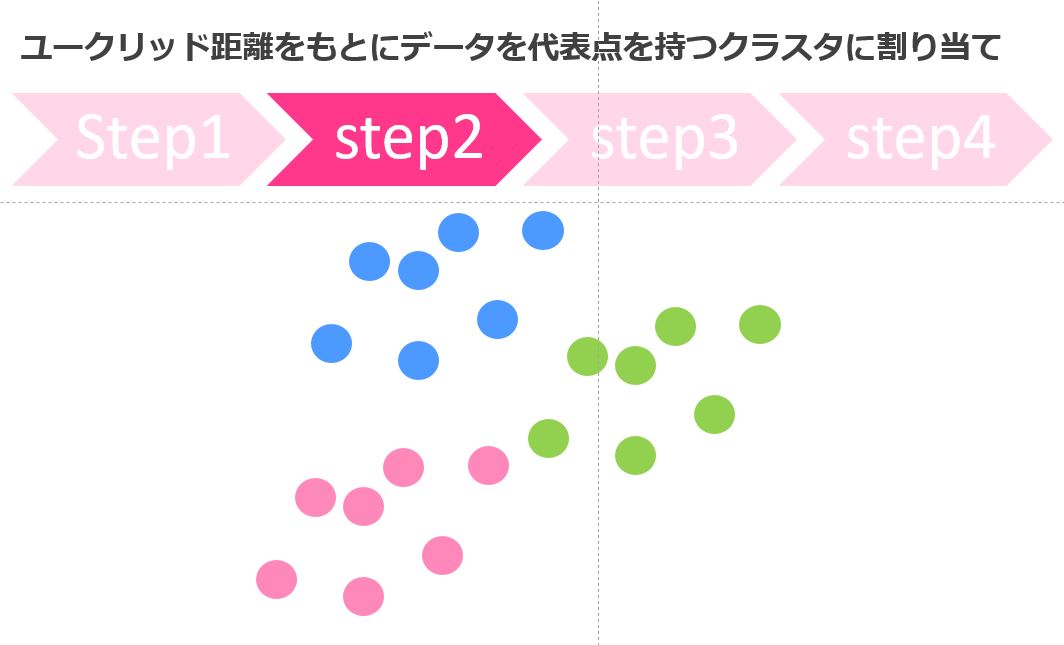
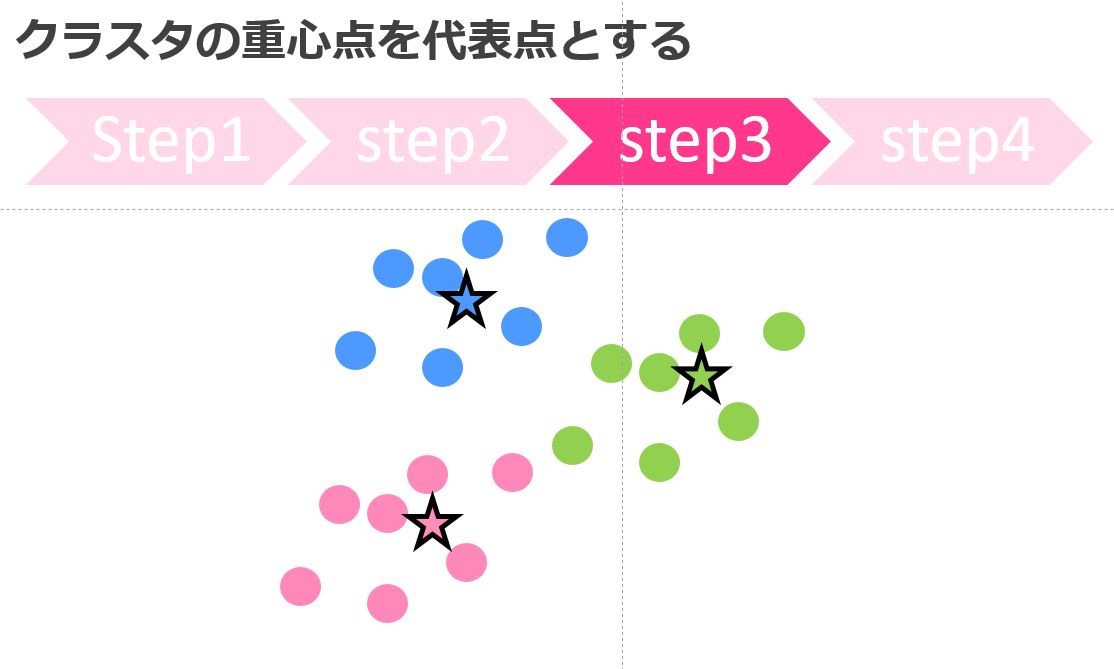
k-means法では、パラメータを基にクラスターの数をあらかじめ決めておきます。
そのクラスターの数に応じて何回かの分類処理を経て最終的にクラスター分けを行うのがk-means法の特徴です。
Rのパッケージで簡単に実装できるのでおこなってみましょうー！
irisというめちゃんこ有名なR内のデータセット（150サンプル5変数で花びらの特徴を表したデータセット）を使います。
3つの花のタイプに分かれているので、そのラベルがk-means法とx-means法で上手く分類できるかどうか見ていきますよー！
実際に行ってみた結果がこちら
■k-means法
| 1 | 2 | 3 | |
| setosa | 0 | 50 | 0 |
| versicolor | 48 | 0 | 2 |
| virginica | 14 | 0 | 36 |
Verginicaは少し外してますが、それ以外は比較的当たってますね！
正答率は89％です。
k-means法について以下の記事でまとめていますのでよければチェックしてみてください！
多変量解析を学ぶ方法
多変量解析について詳しく見てきましたが、どのように勉強すれば良いのか勉強法について見ていきましょう！
多変量解析は統計学の基礎知識を身に付けた後に学ぶ手法群です。
統計学の基礎知識がまだ身に付いていないよ、という方は以下の記事を参考にしてみてください！
書籍で学ぶ
多変量解析に関しては有用な書籍がいくつかあります。
書籍で学べる自信のある人はぜひ書籍で学んでみましょう！
多変量解析入門
多変量解析の幅広い知識を身に付けたいなら手っ取り早いのがこちらの多変量解析法入門。
基礎となる回帰のお話から主成分分析などの話が丁寧に分かりやすく載っています。
単回帰、重回帰、判別分析、主成分分析のところは丁寧に読み込んでおくと良いでしょう。
データ解析モデリング
(2025/07/01 10:47:33時点 Amazon調べ-詳細)
緑本とデータサイエンス界隈で呼ばれる超名著！
多変量解析における回帰系の分析手法から複雑な混合分布を仮定した一般化線形混合モデルの話までの流れを理解しておく上で非常に有用な本です。
多変量解析の世界からベイズ統計学・機械学習への橋渡しに最適です。
他の多変量解析の本に関しても以下の記事でまとめていますのでチェックしてみてくださいね！
Webサービスで学ぶ
多変量解析を学ぶのであればWebサービスを利用してみるのも手です！
手前味噌ですが、以下のUdemy講座で分かりやすく多変量解析の各手法の説明とPython（Rじゃなくてすいません）による実装をまとめています！
【初学者向け】データ分析コンペで楽しみながら学べるPython×データ分析講座
| 【オススメ度】 | |
|---|---|
| 【講師】 | 僕自身！今なら購入時に「DE4947023A44D47EA223」という講師クーポンコードを入れると90%オフ以上の割引価格になりますのでぜひご受講ください！ |
| 【時間】 | 4時間 |
| 【レベル】 | 初級～中級 |
このコースは、なかなか勉強する時間がないという方に向けてコンパクトに分かりやすく必要最低限の時間で重要なエッセンスを学び取れるように作成しています。
アニメーションを使った概要編とハンズオン形式で進む実践編に分かれており、概要編ではYoutubeの内容をより体系的にデータ分析・機械学習導入の文脈でまとめています。
データサイエンスの基礎について基本のキから学びつつ、なるべく堅苦しい説明は抜きにしてイメージを掴んでいきます。
是非興味のある方は受講してみてください！
スタアカ（スタビジアカデミー）で学ぶ
公式サイト：https://toukei-lab.com/achademy/
| 【価格】 | ライトプラン：1280円/月 プレミアムプラン：149,800円 |
|---|---|
| 【オススメ度】 | |
| 【サポート体制】 | |
| 【受講形式】 | オンライン形式 |
| 【学習範囲】 | データサイエンスを網羅的に学ぶ 実践的なビジネスフレームワークを学ぶ SQLとPythonを組みあわせて実データを使った様々なワークを行う マーケティングの実行プラン策定 マーケティングとデータ分析の掛け合わせで集客マネタイズ |
データサイエンティストとしての自分の経験をふまえてエッセンスを詰め込んだのがこちらのスタビジアカデミー、略して「スタアカ」！！
当メディアが運営するスクールです。
多変量解析だけでなくデータサイエンスに必要な広範な範囲を網羅的に学ぶことが可能です！
24時間以内の質問対応と現役データサイエンティストによる1週間に1回のメンタリングを実施します！
カリキュラム自体は、他のスクールと比較して圧倒的に良い自信があるのでぜひ受講してみてください！
他のスクールのカリキュラムはPythonでの機械学習実装だけに焦点が当たっているものが多く、実務に即した内容になっていないものが多いです。
そんな課題感に対して、実務で使うことの多いSQLや機械学習のビジネス導入プロセスの理解などもあわせて学べるボリューム満点のコースになっています！
ウォルマートのデータを使って商品の予測分析をしたり、実務で使うことの多いGoogleプロダクトのBigQueryを使って投球分析をしたり、データサイエンティストに必要なビジネス・マーケティングの基礎を学んでマーケティングプランを作ってもらったり・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践してもらったりする盛りだくさんの内容になってます！
・BigQuery上でSQL、Google Colab上でPythonを使い野球の投球分析
・世界最大手小売企業のウォルマートの実データを用いた需要予測
・ビジネス・マーケティングの基礎を学んで実際の企業を題材にしたマーケティングプランの策定
・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践して稼ぐ
ご受講お待ちしております！
データサイエンティストを目指す人向けのスクールに関しては以下の記事で比較しておりますので是非チェックしてみてください！
多変量解析 まとめ
本記事では、多変量解析の手法とRでの実装、そして最終的には多変量解析の勉強法について見てきました！
最後に多変量解析の種類についてまとめておきましょう！
以下の記事でそれぞれの勉強法についてまとめているのでチェックしてみてください！
スタビジのコンテンツをさらに深堀りしたコンテンツが動画と一緒に学べるスクールです。
プレミアムプランでは私がマンツーマンで伴走させていただきます！ご受講お待ちしております！
