【入門】ディープラーニング(深層学習)の仕組みとPython実装のやり方!

こんにちは!
消費財メーカーでデジタルマーケター・データサイエンティストを経験後、現在は独立して働いているウマたん(@statistics1012)です!
最近はどっぷりディープラーニング(深層学習)に浸かっています。
ディープラーニングのアルゴリズムをブラックボックス的なモノだと考えている方も多いでしょう。
しかし!ディープラーニングの仕組み・考え方は非常にシンプルなのです。
この記事では入門と題していますが、ディープラーニングの基礎的な仕組みからPythonでの実装まで見ていきます。
ちなみにデータサイエンスの基本からディープラーニングまで一気通貫で学びたい方は当サイト「スタビジ」が提供する「スタアカ(スタビジアカデミー)」というサービスで体系的に学ぶことが可能ですので是非チェックしてみてください!

目次
ディープラーニングとは
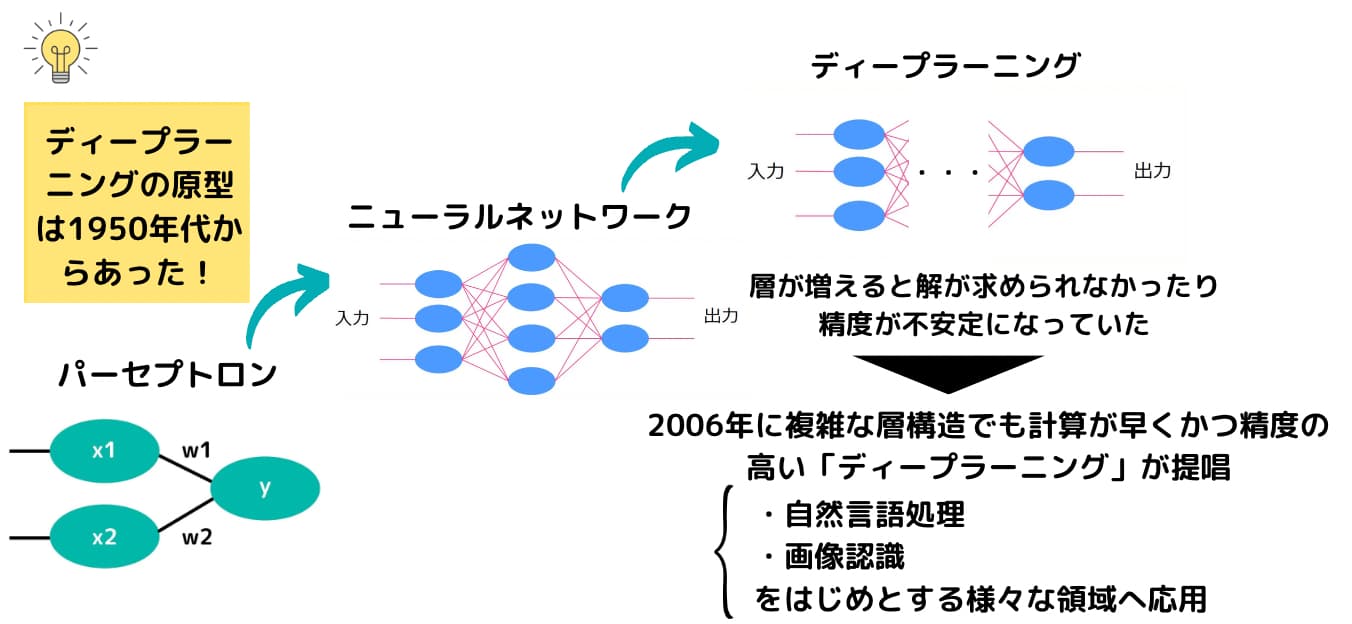
まずはディープラーニングについて簡単に見ていきましょう!
実は、ディープラーニングの原型は1940年代から存在していたと言われています。
1940年~1950年にかけて人間の神経を模した仕組み「ニューラルネットワーク」が確立されました。
人間の神経が信号を伝播させていくようにある入力を次の層へと重み付けをして伝播させていき出力を求めます。
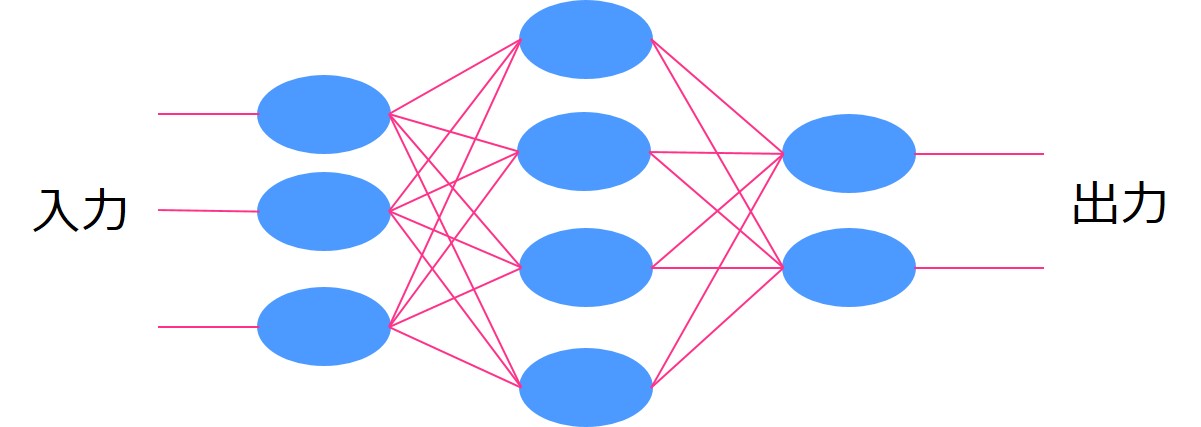
この層を多層にしていくのがディープラーニングなのですが、当時のマシンパワーでは計算量が膨大過ぎて実現不可能でした。
計算負荷を軽減する誤差逆伝播法(バックプロパゲーション)などの計算手法の登場やマシンパワーの増強により現在に至ります。
そんな計算負荷の問題が解消され深層ニューラルネットワーク(ディープラーニング)が日の目を浴びたのは2006年。
このブレークスルーによって再びAIのブームが巻き起こり、第3次AIブームへと突入していくのです。
AIの歴史については以下の記事でまとめていますのでよければご覧ください!

ディープラーニングの仕組み

さて、そんなディープラーニングですがどのような仕組みで成り立っているのでしょうか?
先ほど人間の脳を模した仕組みと述べましたが実際にどのようなカタチで信号が伝播していくのか、そしてその伝播をどのようにチューニングしているのか簡単に見ていきたいと思います。
ディープラーニングの基礎を学ぶ上では以下の書籍が非常に参考になります!
あまりにも有名ですが、是非目を通してみてください。こちらの記事でもこの書籍を参考にしていきます。
ディープラーニングの基本を理解する上で押さえておかなくはいけないのは以下の3点。それぞれについて見ていきます。
・パーセプトロン
・活性化関数
・損失関数と勾配法
パーセプトロン
パーセプトロンとは1957年にアメリカの研究者であるローゼンブラットによって考案されたアルゴリズムです。

パーセプトロンがニューラルネットワークに発展しそこから近年のディープラーニングへと繋がっているのです。
ニューラルネットワークそしてディープラーニングについて学ぶためには、まずはパーセプトロンについて押さえておく必要があります。
パーセプトロンは以下のようなイメージ。
入力\(x_1\)と\(x_2\)に対して重み\(w_1\)と\(w_2\)が掛け合わされ足されます。
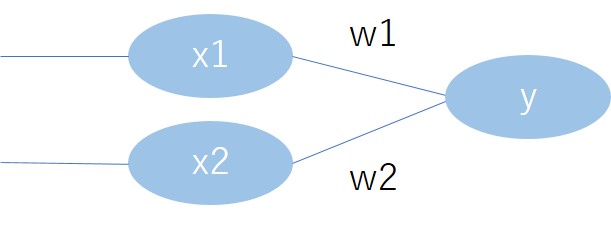
そして、足しあわされた値がある閾値を超えれば\(y\)の出力値が変わるモデルです。
閾値を\({\theta}\)と置き数式で書くと以下のようなモデルになります。
\begin{eqnarray} y= \left\{ \begin{array}{l} 0 (w_1x_1+w_2x_2<=\theta) \\ 1 (w_1x_1+w_2x_2>\theta) \end{array} \right.\end{eqnarray}
この数式をグラフにすると以下のようになりステップ関数と呼びます。
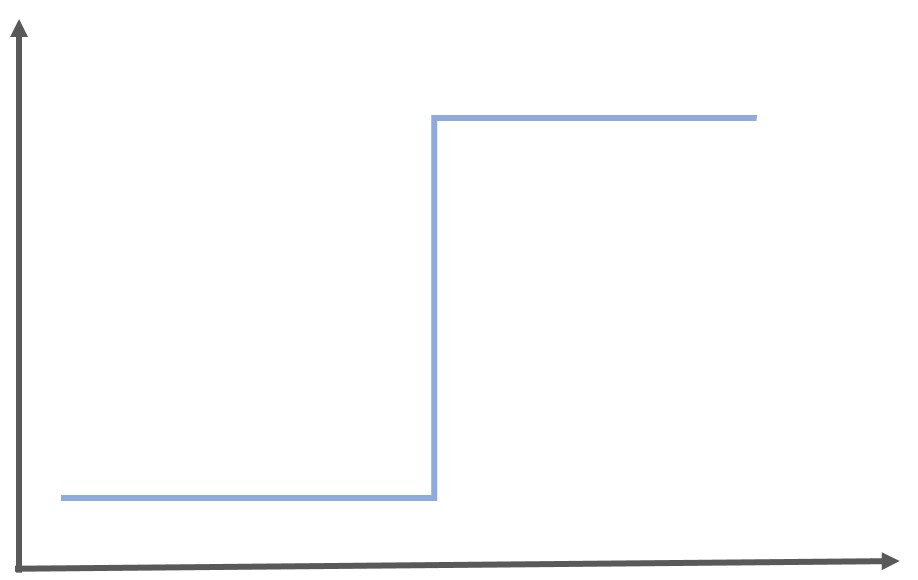
このパーセプトロンに関して真理表を用いた例をPythonでの実装例を含めて「ゼロから作るDeep Leaning」で分かりやすく教えてくれるので興味のある人は是非読んでみてください!
また以下の記事でもパーセプトロンについて詳しく解説しています!

パーセプトロンについては以下のYoutube動画でもかなり詳しく解説しているので是非参考にしてみてください!
活性化関数
パーセプトロンでは、ある閾値を超えた場合に1を出力し超えなければ0であるというステップ関数を用いていました。
これらのインプットからアウトプットに変換する関数を活性化関数と呼び、ディープラーニングを学ぶ上では非常に重要になります。
ディープラーニングでは、活性化関数に様々な関数を用います。
代表的な活性化関数について、それぞれどのような特徴があるのか見ていきましょう!
シグモイド関数
シグモイド関数はロジスティック回帰分析に登場する関数であり出力を線形的に捉えることが可能です。以下のような関数になります。
$$ y= \frac{1}{1+exp(-x)} $$
シグモイド関数の意味は、ある入力に対する出力を0~1の範囲に抑えること。
グラフは以下のようになります。
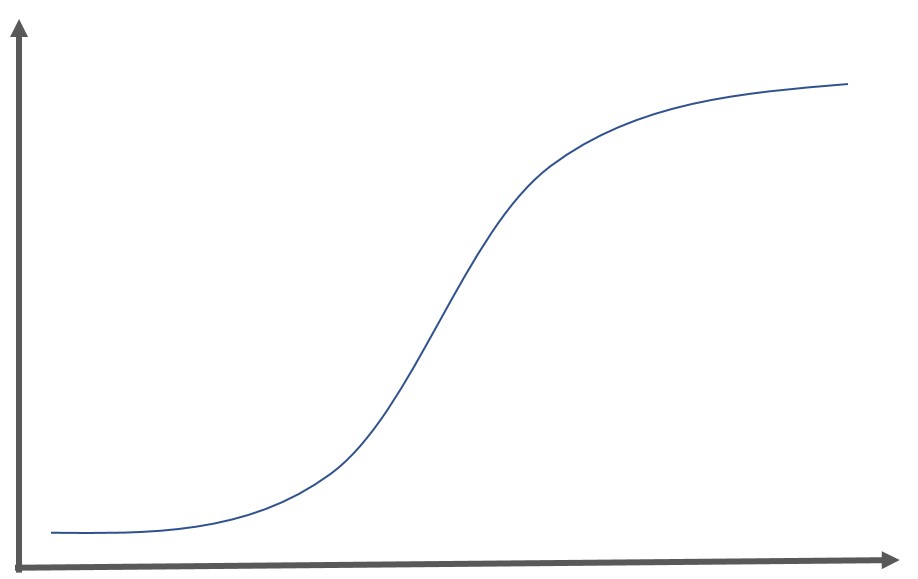
ステップ関数では一定の閾値を超えないと計算結果の大小に限らず同じ値が出力されてしまいますが、シグモイド関数を用いれば微妙な大小を出力の段階で捉えることが可能です。
ロジスティック回帰分析と通常の判別分析の違いと同じですね。
シグモイド関数と似た関数で、Tangent関数があります。
Tangent関数はx,y=(0,0)であるのに対して、シグモイド関数はx,y=(0,0.5)であることが特徴です。
RELU(ランプ)関数
RELU関数は0より小さい場合は0を出力し、0より大きい場合はそのまま計算結果を出力するという特殊な関数です。
\begin{eqnarray} y= \left\{ \begin{array}{l} x ~~ (x>0) \\ 0~~ (x<=0) \end{array} \right.\end{eqnarray}
単純なため計算速度が速いことと、マイナスの値をノイズと捉えたい場合は有用な活性化関数です。画像認識の場面ではマイナスはノイズになるのでRELU関数を用いられることが多いです。
出力層の活性化関数としては非常に貧弱なので、出力層では用いられることはほぼありません。
隠れ層の活性化関数として用いられます。
グラフは以下のようになります。
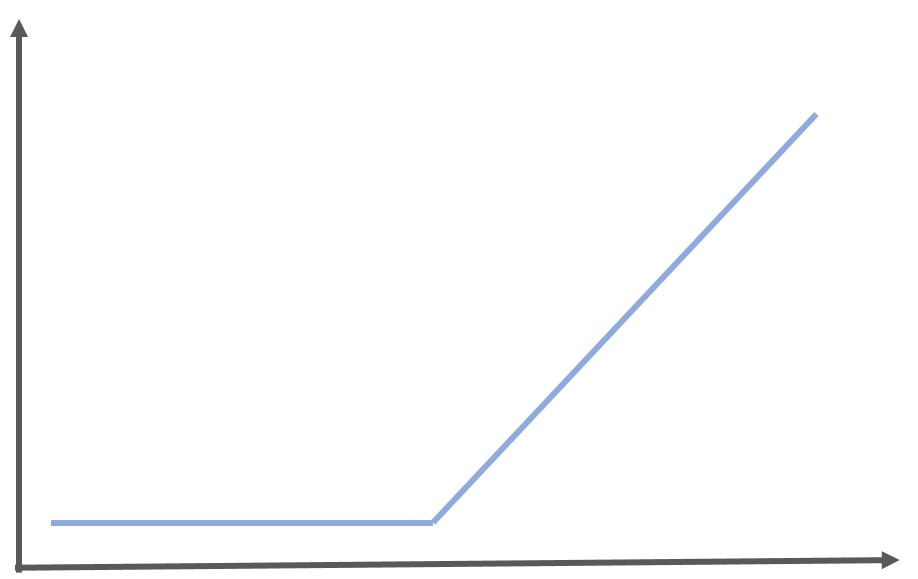
どの活性化関数を用いるかは状況によって違いますが、活性化関数によっては結果が大きく変わってくるので慎重に選ぶことが必要です。
損失関数と勾配法
ディープラーニングでは、基本的にパーセプトロンの考え方で層を積み重ね活性化関数を用いて出力を変化させます。
言ってしまえばそれだけです。
構造は分かりましたが、最適な重みを見つけるためにはどうすればよいでしょう?ここで登場するのが「損失関数と勾配法」という考え方です。
損失関数とはその名の通り損失を定義した関数。ここで言う損失とは何か。
ディープラーニングの層の最終出力と実測値の差
これが損失になります。
損失には二乗誤差やエントロピー誤差が使用されますが基本的には出力と実測値の差を示していると考えて問題ございません。
出力と実測値の差が0なら損失は0です。(ちなみに二乗誤差は回帰問題に、エントロピー誤差は分類問題に使用されます)
出力値を\(y_i\)、実測値を\(t_i\)とすると二乗誤差は以下のようにあらわされます。統計学・機械学習ではお馴染みの式ですね!
$$ \displaystyle \frac{1}{2}\sum_{ i = 1 }^{ n } (y_i-t_i)^2 $$
この時、\(t_i\)は定数であり、変数なのは(\(y_i\)。
どれだけ隠れ層があったとしても、\(y_i\)は入力層からの入力と重み\(w_i\)で表すことができます。つまり\(y_i\)は\(w_i\)の関数で表せるということ。
損失関数を最小限にとどめる\(w_i\)を求めるには\(y_i\)を\(w_i\)で偏微分すれば良い!!高校数学の知識があれば分かると思います。
このようにしてディープラーニングの各層の重みが最適解に決まっていくのです。
この時、偏微分で得られた値をそのまま反映してしまうと局所最適になってしまうので、学習率を設けて徐々にパラメータ\(w_i\)を更新していきます。
これを勾配法と呼ぶのです。
ちなみに偏微分は解析的に数値微分で解く方法もありますが複雑なネットワークだと計算負荷が膨大になるためそれを回避するために誤差逆伝播法が考案されており、現在のディープラーニングにはほぼ誤差逆伝播法が使用されています。
興味のある人は「ゼロから作るDeep Leaning」を読んでみると良いでしょう!
また英語になってしまいますが、誤差逆伝播法に関しては以下の動画がめちゃくちゃ分かりやすいです。
ディープラーニングをPythonで実装するやり方を見てみよう!
今まで見てきたディープラーニングを実際に0から実装してみることも可能ですが、Pythonには便利なライブラリが備わっていてライブラリを読み込むことで誰でも簡単にディープラーニングを実装することが可能です。
隠れ層の数や学習効率などパラメータを調整することは必要ですが、ディープラーニングのフォーマットが提供されておりそれを無料で自由に使用できるのは素晴らしい!
今回は定番のMnistという手書き文字のデータセットを用いて、Kerasというライブラリに入ったディープラーニングを使用して画像認識問題を解いていきます!
KerasはTensorFlowや、CNTK、Theanoなどの、より基本的な機械学習ライブラリを「バックエンド」として呼び出して使うようになっており、ディープラーニングのモデルを層を重ねるイメージで簡単に構築することができるようになっています。
Mnistは「Gradient-based learning applied to document recognition」で用いられたデータセットであり、現在でも多くの論文で用いられています。
Modified National Institute of Standards and Technologyの略であり、0~9の数字が手書き文字として格納されているデータセットです。
学習用に60000枚、検証用に10000枚のデータセットが格納されています。
まずは、必要なライブラリをインストールしていきましょう!
import numpy as np
from sklearn.model_selection import train_test_split
import tensorflow as tf
from tensorflow.keras.datasets import mnist
from tensorflow import keras
from tensorflow.keras.layers import Dense, Activation
from tensorflow.keras.models import Sequential
from tensorflow.keras.utils import to_categoricaltensorflowなどのライブラリはあらかじめpip installしておいてくださいね!
続いてMnistのデータを学習データとテストデータに分けます。
そしてさらに学習データからパラメータチューニングのための検証データを取り出します。
# Kerasに付属の手書き数字画像データをダウンロード
np.random.seed(0)
(X_train_base, labels_train_base), (X_test, labels_test) = mnist.load_data()
# Training set を学習データ(X_train, labels_train)と検証データ(X_validation, labels_validation)に8:2で分割する
X_train,X_validation,labels_train,labels_validation = train_test_split(X_train_base,labels_train_base,test_size = 0.2)この時画像データは、描画がしやすいように28×28の行列になっているのですが、1×784に直しましょう!(畳み込み層を使う場合はそのままでも大丈夫ですがここでは一旦畳み込み層を使わず実装していきます)
さらに0~255のスケールを正規化しましょう!
# 各画像は行列なので1次元に変換→X_train,X_validation,X_testを上書き
X_train = X_train.reshape(-1,784)
X_validation = X_validation.reshape(-1,784)
X_test = X_test.reshape(-1,784)
#正規化
X_train = X_train.astype('float32')
X_validation = X_validation.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_validation /= 255
X_test /= 255続いてラベルをダミー変数化します。
# labels_train, labels_validation, labels_test をダミー変数化して y_train, y_validation, y_test に格納する
y_train = to_categorical(labels_train)
y_validation = to_categorical(labels_validation)
y_test = to_categorical(labels_test)ここでデータの成型が終了したので、ディープラーニングのネットワーク構築に入ります。
隠れ層では、RELU(ランプ)関数を用いて出力層ではソフトマックス関数を用いています。
Model.addを使うことで隠れ層をいくつも積み重ねることが可能です。
# パラメータの設定
n_features = 784
n_hidden = 100
bias_init = 0.1
# 学習率
rate = 0.01
# Sequentialクラスを使ってモデルを準備する
model = Sequential()
# 隠れ層を追加
model.add(Dense(n_hidden,activation='relu',input_shape=(n_features,)))
model.add(Dense(n_hidden,activation='relu'))
model.add(Dense(n_hidden,activation='relu'))
# 出力層を追加
model.add(Dense(10,activation='softmax'))
ネットワークの構築が終了した後は、最適な重みを見つけていきます。
AdamOptimizerは最近よく使われている最適化手法です。
Early stoppingとはもう精度が改善しないようなら学習を止めてしまう条件です。
これによってムダな学習を省くことが可能です。
最後のvalidation_dataで過学習が起こらないように検証を行っています。
# TensorFlowのモデルを構築
model.compile(optimizer=tf.optimizers.Adam(rate),
loss='categorical_crossentropy', metrics=['mae', 'accuracy'])
# Early stoppingを適用してフィッティング
log = model.fit(X_train, y_train, epochs=3000, batch_size=100, verbose=True,
callbacks=[keras.callbacks.EarlyStopping(monitor='val_loss',
min_delta=0, patience=10,
verbose=1)],
validation_data=(X_validation, y_validation))最後にテストデータで予測を実行して実測値と予測値の正解率を求めます!
# テストデータの出力から0~9のどの値か判断
pred_test = np.argmax(model.predict(test_x), axis=1)
sum(pred_test == test_y)/len(pred_test)最終的な結果は・・・・96.96%!!
そこそこな精度をたたき出すことができました。パラメータをいじることで精度を99%まで伸ばしてみてください!
最後にまとめてコードを載せておきます。
畳み込みニューラルネットワーク(CNN)をPythonで実装するやり方を見てみよう!
先程はあえて畳み込み層を利用せず単純な層構造で実装してみましたが、続いては畳み込み層を利用して実装していきましょう!
以下のように実装していきます。
基本的に実装フローは変わらないのですが、Kerasで定義する層構造が違います。
model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.Flatten())
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(10, activation='softmax'))Conv2Dで2次元畳み込み層を定義しています。
手書き文字が28×28×1のデータなので、畳み込み層へのインプットの際に以下のようになっていることに注意しましょう!
model.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)))また最後の出力層では、0~9の10種類の文字なので以下のように出力カテゴリが10になっていることに注意しましょう!
model.add(layers.Dense(10, activation='softmax'))
CNNに関して詳しくは以下の記事をチェックしてみてください!

ちなみに勾配ブースティング手法である、Xgboost・LightGBM・CatboostでもMnistデータの分類をおこなっているので是非チェックしてみてください!

また、ここではMnistを扱いましたが絵画画像を使った実践的な画像認識に関しては以下の記事でまとめています!

おまけ:RNNをPythonで実装するやり方を見てみよう!

おまけ的にPython実装をおこなっていきましょう!
通常のディープラーニングでは、時系列問題を上手く扱えません。
そこで登場するのがリカレントニューラルネットワーク(RNN)!
今までのディープラーニングでは、それぞれのインプットがそれぞれの中間層に与えられていましたが、RNNでは同一の中間層を用いて再帰的にインプットが行われます。
再帰的という部分がReccurentと言われるゆえんです。
こんな感じ。
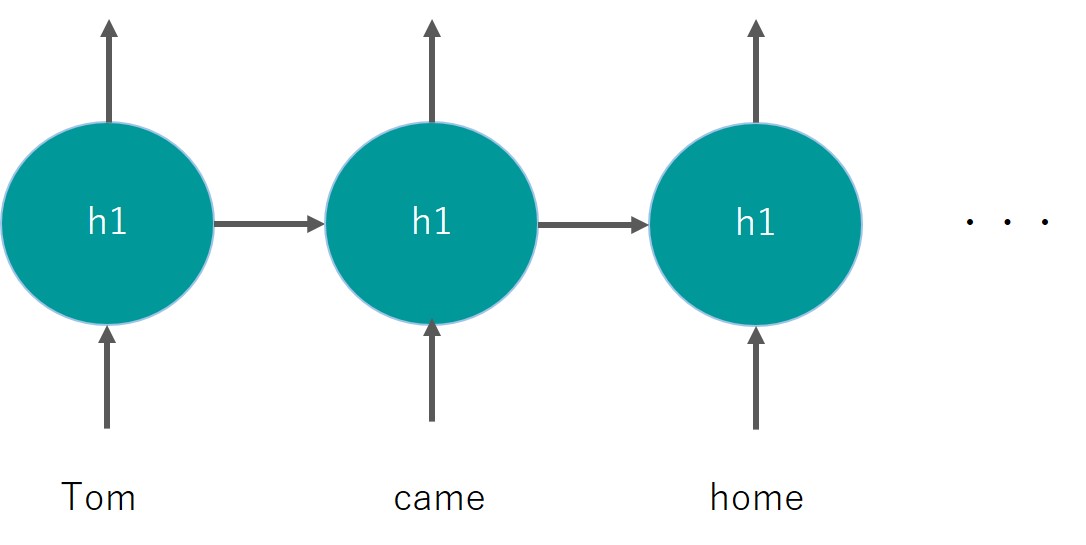
分かりづらいかも!
詳しくは以下の記事でまとめているのでチェックしてみてください!

ここでは、このRNNも簡単にPythonで実装できるんだよーってことを見ていきます!
使うデータセットはKaggleのホームページが落とせる航空会社の乗客数データ!
1949年から1960年までの月別乗客数がデータとして入っています。
149行2列のシンプルなデータセット。
モデル構築は以下のサイトを参考にしています。
1変数の時系列データを基に過去のデータから未来の値を予測します。
この時、tflearnというライブラリを使ってRNN(正確にはLSTM)を実装していきます。tflearnはkerasと似たようなライブラリでディープラーニングの実装が感覚的に容易にできます。
実際にモデルを構築していきましょう!
最終的な評価はRMSE(Root Mean Square Error)で算出しています。
細かい実装ポイントについて見ていきましょう!
def create_dataset(dataset, steps_of_history, steps_in_future):
X, Y = [], []
for i in range(0, len(dataset)-steps_of_history, steps_in_future):
X.append(dataset[i:i+steps_of_history])
Y.append(dataset[i + steps_of_history])
X = np.reshape(np.array(X), [-1, steps_of_history, 1])
Y = np.reshape(np.array(Y), [-1, 1])
return X, Y
def split_data(x, y, test_size=0.1):
pos = round(len(x) * (1 - test_size))
trainX, trainY = x[:pos], y[:pos]
testX, testY = x[pos:], y[pos:]
return trainX, trainY, testX, testYここでは、データセットを時系列モデルに適した形に変形する関数と学習データ予測データに分ける関数を作っています。
net = tflearn.input_data(shape=[None, steps_of_history, 1])
net = tflearn.lstm(net, n_units=6)
net = tflearn.fully_connected(net, 1, activation='linear')
net = tflearn.regression(net, optimizer='adam', learning_rate=0.001,
loss='mean_square')
model = tflearn.DNN(net, tensorboard_verbose=0)
model.fit(trainX, trainY, validation_set=0.1, batch_size=1, n_epoch=150)ここが実際にRNN(LSTM)モデルを構築している部分。
ちなみに初回モデル構築は問題ないですが、再度パラメータを変えて処理を回そうとするとJupyter notebookではエラーをはいてしまうので、7行目に初期化するような記述を入れています。
tensorflow.reset_default_graph() #モデルを初期化これだけでRNNが実装できちゃうんです!簡単!
この時、RMSEは0.10079201となりました。それなりに良い予測ができてる!
ちなみに層を増やしてみると・・・
net = tflearn.input_data(shape=[None, steps_of_history, 1])
net = tflearn.lstm(net, n_units=6, activation='relu',return_seq=True )
net = tflearn.lstm(net, n_units=6, activation='relu')
net = tflearn.fully_connected(net, 1, activation='linear')
net = tflearn.regression(net, optimizer='adam', learning_rate=0.001,
loss='mean_square')RMSEは0.16051404に悪化してしまいました・・・
簡易的なデータセットに複雑なモデルで当ててもあまり意味がなさそう。
ちなみに過学習を防ぐためにDropoutなどのパラメータで調節することも可能です!
ディープラーニング まとめ

ここまでご覧いただきありがとうございました!
本記事ではディープラーニングについて見てきましたが、非常にシンプルな仕組みでありかつPythonを使えば簡単に実装できることが理解いただけたでしょうか?
意外とちゃんと見ていくとシンプルなディープラーニングなのですが、効果は絶大!
簡単な例ですが画像認識を相当な精度で実現できたのはディープラーニングの素晴らしさをひしひしと感じますねー!
とは言え、まだまだここで紹介したのはディープラーニングの入門の入門です。
ディープラーニングの領域は研究が盛んで日々様々な手法が生み出されています。
この記事で何度も紹介してきましたが、以下の書籍がディープラーニングの理論を理解するにはうってつけなので興味のある人は是非読んでみてください!
ディープラーニングの勉強法に関しては以下の記事でまとめていますので、ぜひ参考にしてみてください!

ディープラーニングの仕組みや実装をより詳しく学びたいという方は当サイト「スタビジ」が提供する「スタアカ(スタビジアカデミー)」というサービスで体系的に学ぶことが可能ですので是非参考にしてみてください!
AIデータサイエンス特化スクール「スタアカ」

| 【価格】 | ライトプラン:1280円/月 プレミアムプラン:149,800円 |
|---|---|
| 【オススメ度】 | |
| 【サポート体制】 | |
| 【受講形式】 | オンライン形式 |
| 【学習範囲】 | データサイエンスを網羅的に学ぶ 実践的なビジネスフレームワークを学ぶ SQLとPythonを組み合わせて実データを使った様々なワークを行う マーケティングの実行プラン策定 マーケティングとデータ分析の掛け合わせで集客マネタイズ |
データサイエンティストとしての自分の経験をふまえてエッセンスを詰め込んだのがこちらのスタビジアカデミー、略して「スタアカ」!!
当メディアが運営するスクールです。
24時間以内の質問対応と現役データサイエンティストによる複数回のメンタリングを実施します!
カリキュラム自体は、他のスクールと比較して圧倒的に良い自信があるのでぜひ受講してみてください!
他のスクールのカリキュラムはPythonでの機械学習実装だけに焦点が当たっているものが多く、実務に即した内容になっていないものが多いです。
そんな課題感に対して、実務で使うことの多いSQLや機械学習のビジネス導入プロセスの理解なども合わせて学べるボリューム満点のコースになっています!
Pythonが初めての人でも学べるようなカリキュラムにしておりますので是非チェックしてみてください!
ウォルマートのデータを使って商品の予測分析をしたり、実務で使うことの多いGoogleプロダクトのBigQueryを使って投球分析をしたり、データサイエンティストに必要なビジネス・マーケティングの基礎を学んでマーケティングプランを作ってもらったり・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践してもらったりする盛りだくさんの内容になってます!
・BigQuery上でSQL、Google Colab上でPythonを使い野球の投球分析
・世界最大手小売企業のウォルマートの実データを用いた需要予測
・ビジネス・マーケティングの基礎を学んで実際の企業を題材にしたマーケティングプランの策定
・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践して稼ぐ
ディープラーニングの学習をしっかり集中的に行うのであれば他のプログラミングスクールもオススメです。
以下の記事でまとめているのでぜひチェックしてみてください!

























