こんにちは！スタビジ編集部です！
損失関数、機械学習に触れたことがある方なら一度は聞いたことありますよね？？
機械学習ライブラリではデフォルトで設定されているものを使うことが多いので、その辺りについて詳しく知っている人はあまり多くないかも知れません。
しかし、損失関数についての理解を深めることでより精度の高いモデルを作成することができます！
この記事では、そんな損失関数について、その種類から具体的な事例まで詳しく解説していきます！
目次
損失関数とは
損失関数とは、実際の値と予測値の差の測り方を定めた関数のことです！
損失関数の出力が小さなモデルであるほど、より精度の高いモデルであると言えます。
では、損失関数はどのような場面で用いられるのでしょうか？
例えばニューラルネットワークでは、損失関数の出力がより小さくなるようにパラメータを繰り返し更新していき、その出力が最小となったときのパラメータを最終的なモデルのパラメータとします。
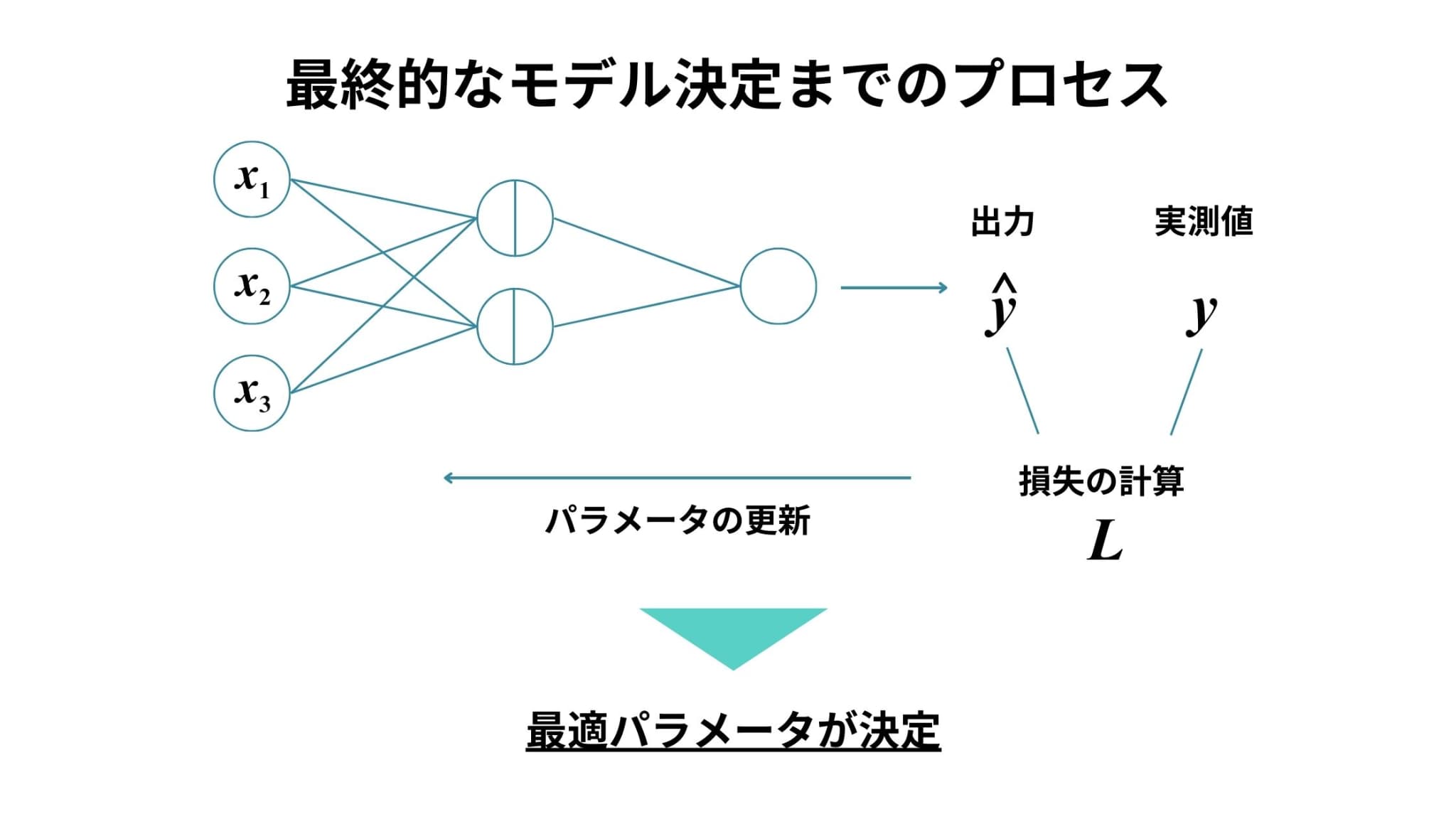
損失関数という言葉は、このようなパラメータを逐一更新するような機械学習手法のプロセスで用いられることが多いですが、基本的に教師あり学習のどの手法にも存在します（回帰分析における残差平方和も損失関数の1つ）。
損失関数の種類
損失関数には様々な種類のものがあります。
ここでは、回帰問題、分類問題それぞれでよく用いられる損失関数を紹介していきます。
なお、ここで紹介する損失関数はモデルの最終的な評価指標としても用いられる場合がありますが、あくまでモデルの学習の際に用いられているということに注意してください。
回帰問題で用いられる損失関数
MSE（平均二乗誤差/Mean Squared Error）
MSEは、回帰問題において最もメジャーな損失関数です。
\(y_{i}\)を実測値、\(\hat y_{i}\)を予測値としたとき、その差の２乗の平均値がMSEとなります。
MSEを用いるメリットとしては、予測誤差が大きいほど過大に評価（=間違いをより重視）するので、より差を付けて評価しやすくなる（損失関数として見るなら学習しやすくなる）というものがあります。
デメリットとしては、外れ値に対しても敏感になるため、外れ値にも過剰適合してしまうということがあります。
\(\displaystyle MSE (y_{i},\hat y_{i})=\frac{1}{n}\sum_{i=1}^{n}(y_{i}-\hat y_{i})^2\)
MAE（平均絶対誤差/Mean Absolute Error）
MAEも用いられることが多い損失関数です。
\(y_{i}\)を実測値、\(\hat y_{i}\)を予測値としたとき、その差の絶対値の平均値がMAEとなります。
MAEを用いるメリットとしては、予測誤差を二乗しないため、外れ値に強い（外れ値に適合しにくい）というものがあります。
デメリットとしては、損失関数の微分が常に一定になるので、損失関数の出力がどんな値であったとしても同じスピードで学習を進めてしまうというものがあります。つまり、損失関数の出力が小さい場合に細かな学習（より最適なパラメータの探索）がしにくくなってしまうというわけです。
\(\displaystyle MAE (y_{i},\hat y_{i})=\frac{1}{n}\sum_{i=1}^{n}\left|y_{i}-\hat y_{i}\right|\)
Huber損失
Huber損失は、損失関数の出力が大きいとMAEに似た機能をし、出力が小さいとMSEの機能になるという関数です。
MSEとMAEの良いとこどりであると言えますね！
それぞれの切り替わりは\(\delta\)というパラメータで設定します。
これにより、外れ値に寛容でありながらMAEのデメリットを克服することができます。
\(\displaystyle L(y_{i},\hat y_{i})=\begin{cases}\frac{1}{2}(y_{i}-\hat y_{i})^2 & \left|y_{i}-\hat y_{i}\right| \leq \delta \\ \delta(\left|y_{i}-\hat y_{i}\right|-\frac{1}{2}\delta) & \left|y_{i}-\hat y_{i}\right| > \delta \end{cases}\)
ポアソン損失
ポアソン損失は、主にカウントデータで用いられる損失関数です。
その名の通り、ポアソン分布が元である損失間数となっています。
\(\displaystyle L(y_{i},\hat y_{i})=\frac{1}{n}\sum_{i=1}^{n}(\hat y_{i}-y_{i}\log \hat y_{i})\)
分類問題で用いられる損失関数
交差エントロピー
交差エントロピーは、分類問題において最もメジャーな損失関数です。
エントロピーとは不確定性の尺度のことで、どれだけ予想と実際のギャップがあるのかを示す指標です。
つまり、実測値の確率分布（\(p(k)\)）と予測値の確率分布（\(q(k)\)）の近さを表現しているということです。
交差エントロピーのメリットとしては、正解から離れるほど誤差が急激に大きくなるので、学習の速度が速いというものがあります。
\(\displaystyle E (p(k),q(k))=-\sum_{k}p(k)\log q(k)\)
なお、scikit-learnで勾配ブースティングなどを利用する際、損失関数のデフォルト設定がlog_lossというものになっていますが、これは交差エントロピーと同じものです。
損失関数の選択
本記事の冒頭で「損失関数の理解を深めるとより精度の高いモデルを作成することができる」と述べましたが、これは最適な損失関数を選択することでより高い精度のモデルが得られるということです。
そこで、どんな場合に損失関数の選択が有効であるのか、事例を紹介していきます。
データに外れ値が存在する場合
外れ値が存在する場合、選択する損失関数によってモデルの予測精度が変わる可能性があります。
例えば、MAEを損失関数に用いることで、外れ値の影響を受けにくいようなモデルを作成することができます。
ただし、他のデータの予測能力が劣ってしまうということがあるので、外れ値がそこまで重要でないのならMSEを用いるべきです。
また場合によってはHuber損失を用いることで、それらよりも高い精度を見込めるかも知れません。
データの分布が特殊な場合
データの分布が特殊な（正規分布ではない）場合にも、選択する損失関数によってモデルの予測精度が変わる可能性があります。
例えば上でも紹介したように、ポアソン損失はポアソン分布に従うようなデータに対して適用すべき損失関数です。
カウントデータを用いた予測モデルを作成する場合、MSEやMAEを用いるよりもより良い精度を得られる可能性が高いです。
不均衡データである場合
不均衡データである場合にも、選択する損失関数によってモデルの予測精度が変わる可能性があります。
不均衡データとは、データの比率に偏りがあるもののことです。
このようなデータをそのまま分析すると、一見良さそうに思えても実際は意味のない結果が出てきてしまいます。
そこで不均衡データに対応した損失関数を選択することで、そのような問題を回避しより良い予測精度を得ることができます。
詳しい説明は省きますが、そのような損失関数としてFocal Lossというものがあります。
まとめ
本記事では、損失関数について解説していきました。
今回紹介したもの以外にも様々な損失関数があります。
他にどのような損失関数があるのかについて興味がある方は是非調べてみてください！
またデータ分析の際は、特徴量エンジニアリングに加え、損失関数の観点も意識することでより高い精度を得られるでしょう！
さらに詳しくAIやデータサイエンスの勉強がしたい！という方は当サイト「スタビジ」が提供するスタビジアカデミーというサービスで体系的に学ぶことが可能ですので是非参考にしてみてください！
AIデータサイエンス特化スクール「スタアカ」
| 【価格】 | ライトプラン：1280円/月 プレミアムプラン：149,800円 |
|---|---|
| 【オススメ度】 | |
| 【サポート体制】 | |
| 【受講形式】 | オンライン形式 |
| 【学習範囲】 | データサイエンスを網羅的に学ぶ 実践的なビジネスフレームワークを学ぶ SQLとPythonを組み合わせて実データを使った様々なワークを行う マーケティングの実行プラン策定 マーケティングとデータ分析の掛け合わせで集客マネタイズ |
データサイエンティストとしての自分の経験をふまえてエッセンスを詰め込んだのがこちらのスタビジアカデミー、略して「スタアカ」！！
当メディアが運営するスクールです。
24時間以内の質問対応と現役データサイエンティストによる複数回のメンタリングを実施します！
カリキュラム自体は、他のスクールと比較して圧倒的に良い自信があるのでぜひ受講してみてください！
他のスクールのカリキュラムはPythonでの機械学習実装だけに焦点が当たっているものが多く、実務に即した内容になっていないものが多いです。
そんな課題感に対して、実務で使うことの多いSQLや機械学習のビジネス導入プロセスの理解なども合わせて学べるボリューム満点のコースになっています！
Pythonが初めての人でも学べるようなカリキュラムしておりますので是非チェックしてみてください！
ウォルマートのデータを使って商品の予測分析をしたり、実務で使うことの多いGoogleプロダクトのBigQueryを使って投球分析をしたり、データサイエンティストに必要なビジネス・マーケティングの基礎を学んでマーケティングプランを作ってもらったり・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践してもらったりする盛りだくさんの内容になってます！
・BigQuery上でSQL、Google Colab上でPythonを使い野球の投球分析
・世界最大手小売企業のウォルマートの実データを用いた需要予測
・ビジネス・マーケティングの基礎を学んで実際の企業を題材にしたマーケティングプランの策定
・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践して稼ぐ
スタビジのコンテンツをさらに深堀りしたコンテンツが動画と一緒に学べるスクールです。
プレミアムプランでは私がマンツーマンで伴走させていただきます！ご受講お待ちしております！
