回帰分析の理論とRでの実装!

こんにちは!
この記事では最も一般的でビジネスシーンでもよく使われる「回帰分析」について説明していきます!
データ解析手法の中で最もシンプルですが最も重要で様々なところで使われます。なめちゃいけません。
回帰分析ってなに?

回帰分析についてざっくり説明していきます。
以下の動画でも解説していますよ!
回帰分析とは「ある変数を用いて他の変数を説明(予測)するモデルを作ること」です。
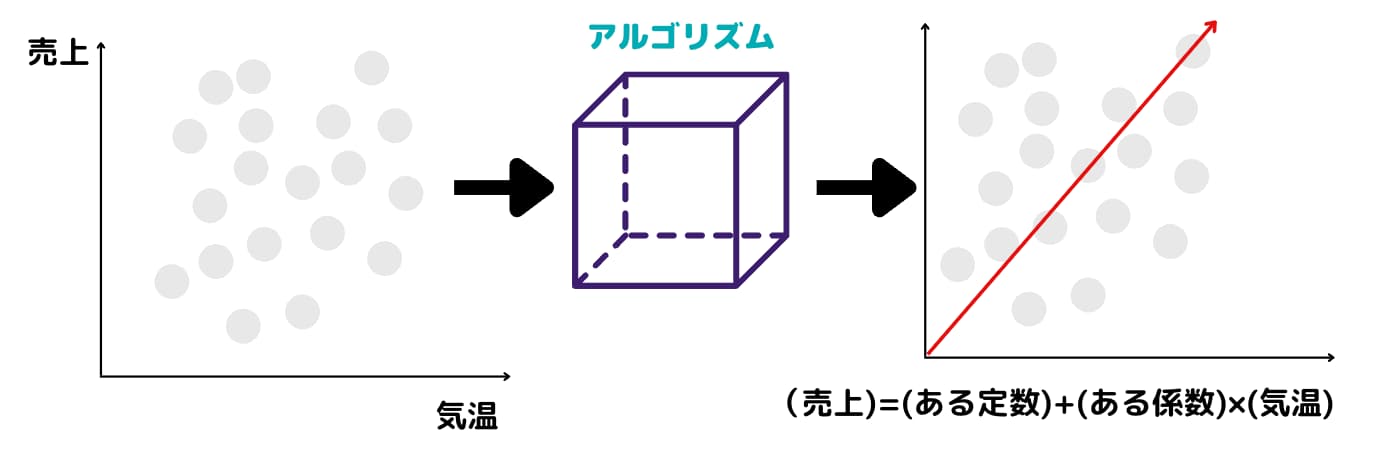
例えば、「ある日のアイスの売上高をその日の気温で説明したい!」というときに使います。
$$(アイスの売上高)=(ある定数)+(ある係数)\times(気温)$$
というモデルを作ることが出来ます。
ここで、(アイスの売上高)のことを目的変数あるいは従属変数、(気温)のことを説明変数あるいは独立変数と呼びます。
回帰分析の方法はたくさんあり、目的変数の形式によっても変わったりします
例えば、目的変数が割合や二値データの場合はロジスティック回帰分析、カウントデータの場合はポアソン回帰分析になります。
回帰という言葉は機械学習でも出てきますが、それはつまり「何かの値を予測したい」という風に捉えればOKです。
機械学習に関してはこちらにまとめていますのであわせてご覧ください!

回帰分析のアルゴリズム

回帰分析を式で表して理解していきます。
先ほどは(アイスの売上高)などを使いましたが記号を使って式にしてみます。
n個のサンプルがあるデータセットで一つの目的変数をp個の説明変数で説明するモデルを作ると以下のようになります。
$$y_i=\beta_0+\beta_1x_{i1}+\cdots+\beta_px_{ip}+\epsilon_i, \epsilon_i \sim N(0,\sigma^2),(i=1,\cdots,n)$$
\(y\):目的変数、\(\beta_0\):ある定数、\(\beta_j\):ある係数、\(\epsilon\):誤差項を表しています。また添え字のiはサンプルを表します。
ベクトルで表記すると次のように書き換えられます。
\begin{eqnarray*}
{\bf y}&=&{\bf X}{\bf \beta}+{\bf \epsilon},{\bf \epsilon} \sim N({\bf 0},\sigma^2{\bf I_n})\\
\end{eqnarray*}
\({\bf y}\):n次元ベクトル、\({\bf X}\):n×(p+1)の行列ただし一列目は1を並べた列、\({\bf \beta}\):(p+1)次元ベクトル、\({\bf \epsilon}\):n次元ベクトル。
回帰分析では\({\bf \beta}\)を求めることが目的になります。
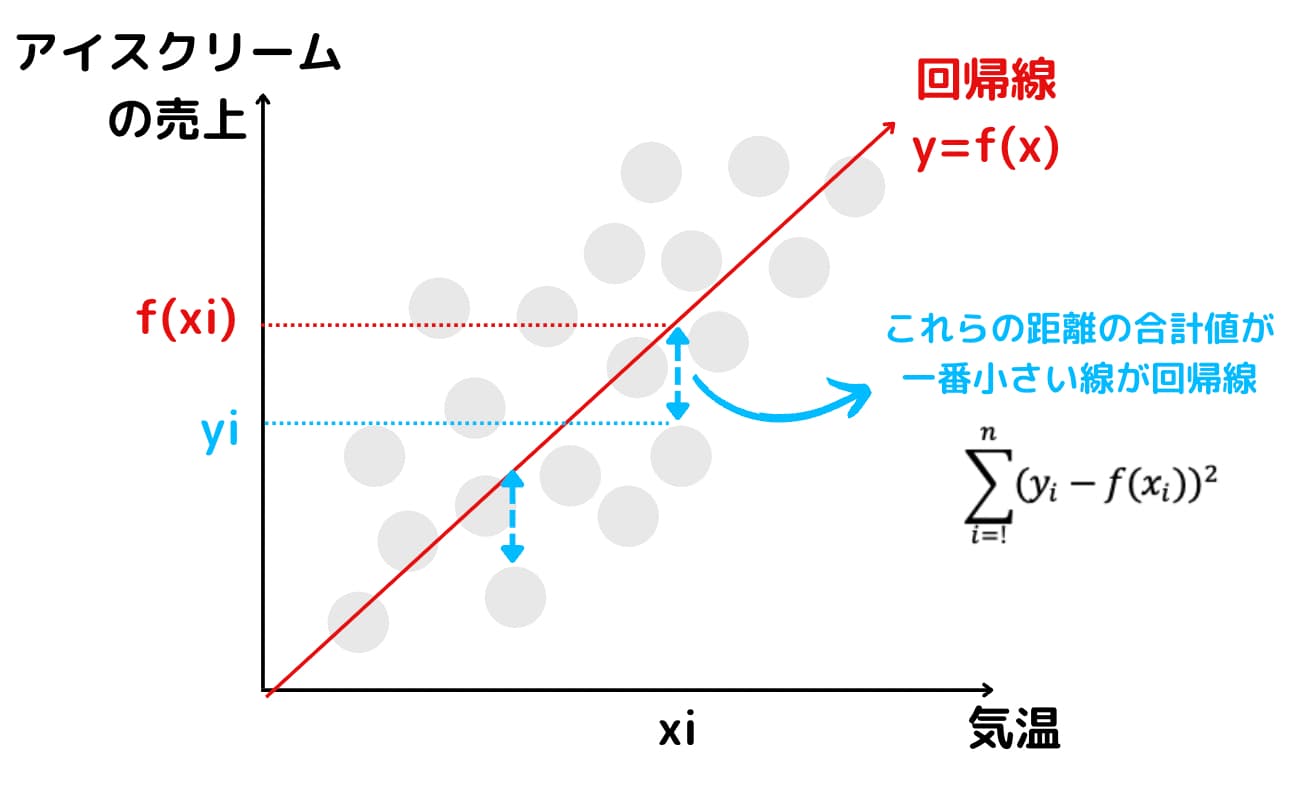
ではどのように求めるかと言うとデータがモデル式によく当てはまるように求めます。この方法を最小二乗法と言います。
具体的には残差平方和を最小化する\({\bf \beta}\)を求めることになります。
少しの微分の計算によって\({\bf \beta}\)は次のように求められます。
\begin{eqnarray*}
\hat{{\bf \beta}}&=&{({\bf X}^{T}{\bf X})}^{-1}{\bf X}^{T}{\bf y}\\
\end{eqnarray*}
従って、\({\bf y}\)の推定値\(\hat{{\bf y}}\)は次のようになります。
\begin{eqnarray*}
\hat{{\bf y}}&=&{\bf X}{({\bf X}^{T}{\bf X})}^{-1}{\bf X}^{T}{\bf y}\\
\end{eqnarray*}
回帰分析の弱点

さて、ここで気になることがあります。それは\({({\bf X}^{T}{\bf X})}^{-1}\)が必要だということです。
実は、説明変数の相関が非常に高かったり従属関係にある場合に\({({\bf X}^{T}{\bf X})}\)の逆行列が計算出来なくなります。
この問題を多重共線性と言います。
多重共線性が起きていると回帰分析は解析が出来なくなってしまいます。
多重共線性を回避するためには相関の高い変数を解析から外す(変数選択)などの処置が必要になります。
しかし、変数の数があまりにも多すぎたりすると変数選択も難しくなります。
そんなときにはいくつかの変数を一つの合成変数にまとめてしまう主成分回帰やPLS回帰などの方法やパラメータについての制約を与えることで解析可能にする正則化手法などがあります。
回帰分析の応用

回帰分析と言えば、線形回帰分析という今回のような回帰分析が一番シンプルで有名ですが、線形回帰分析はデータセットに正規分布を想定しておりシンプルなモデルになっています。
しかし現実世界のデータは正規分布に従っていないことも多くそんなにシンプルではないことが多々あります。
そこでデータ構造にポアソン分布や2項分布などを想定した一般化線形回帰分析という手法があります。
また、データがスパースな時に使われる手法もあります。世の中のデータを解析するときにはパラメータは0と推定したいことが多くあります。
説明変数が多い場合に目的変数に関係ない説明変数への係数は0と推定したいです。
このとき通常通りに最小二乗法を行い、AICなどの基準によって変数選択を行っても良いのですが、サンプルサイズよりパラメータが多い場合にはそもそも解析できないということがあります。
そんなときに、スパース推定をすることで回帰係数の推定と変数選択を同時に行うことができるという利点があります(この手法はLasso回帰と呼ばれます)。
というように実は回帰分析は奥が深く様々な応用手法が存在するのです。
回帰分析を実際にRで実装してみよう

それでは最後に回帰分析を実際に実装してみます。
今回は線形回帰モデルの人工データを用いて線形回帰・Lasso・Ridgeの精度比較を行います。
実験の設定と手順
・比較手法:通常の線形回帰・Lasso回帰・Ridge回帰
・評価指標:MSPE(平均二乗予測誤差)
・シミュレーション回数:100回
実験の流れは簡単にこんな感じです。
- 人工データを生成
- データを解析
- 指標を算出して結果を格納
- 1~3を100回繰り返す
- 結果の平均とばらつきで比較
人工データ生成
今回のデータの生成モデルを次に示します。
\begin{eqnarray*}
y_i&=&1+{\bf x}_i^T{\bf \beta}+\epsilon_i\\
{\bf \beta}&=&(1,-1,0,\cdots,0)^T\in {\bf R}^p\\
{\bf x_i}&\sim& N({\bf \mu},{\bf \Sigma})\\
{\bf \mu}&=&{\bf 0}_p\\
{\bf \Sigma}&=&{\bf I}_p\\
\epsilon_i&\sim& N(0,1^2)\\
i&=&1,2,\cdots,n\\
\end{eqnarray*}
説明変数は\(p\)次元であり、平均0・独立で発生させています。
また、\(\beta\)はp次元ベクトルであり、変数1と変数2のみが目的変数へ寄与があります。
つまり、かなりスパースな設定になっています。
今回は、\(p\)を5,10,50と変化させて実験してみます。
シミュレーション実験
シミュレーション実験をしてみましょう。
サンプルサイズ\(n\)は1100とします。
100個のデータを学習データ、残りの1000個のデータをテストデータとして実験します。
今回用いるコード(\(p=50\)の場合)を載せておきます。
実行する前に入っていないパッケージはインストールしておいてください。
ばらつきも含めて見たいので結果を箱ひげ図で表します。
通常の線形回帰はglmと表記してあります。
・\(p=5\)の結果
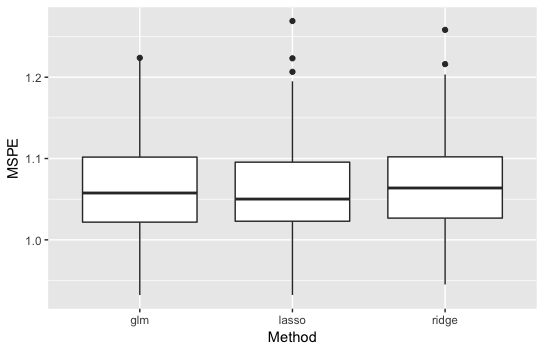
説明変数の数も多くないのであまり手法の差は見えません。
・\(p=10\)の結果
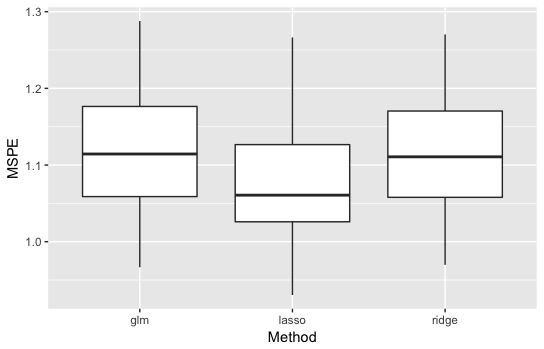
通常の線形回帰とRidgeは同じくらいですが、Lassoが良い精度を示しています。
説明変数が多くなってスパース性が上がったことが原因でしょう。
・\(p=50\)の結果
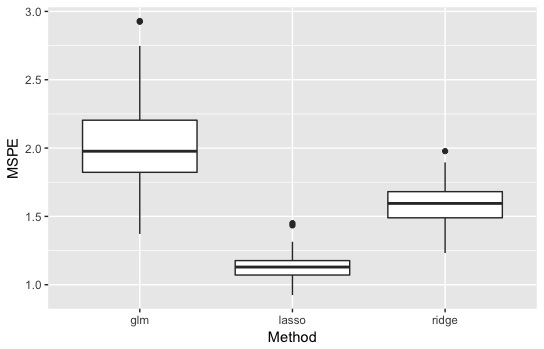
通常の線形回帰が最も悪くなり、Lassoが最も良くなりました。
差もかなり大きいです。
Lasso回帰・Ridge回帰に関してはこちらの記事も参考にしてみてください!

回帰分析 まとめ
最後に少々複雑な分析を行いましたが、基本的に回帰分析はRやPythonを使えば一瞬で出来ちゃう単純な手法です!
Excelでも問題なく実装することが可能!
Excelでの回帰分析の実装は以下にまとめています!

最後に回帰分析についてポイントをまとめておきましょう!
・回帰分析はビジネスでも汎用性が高い手法
・多重共線性という問題があるので注意
・様々な発展的手法が存在する
・線形回帰分析は簡単に実装が可能
回帰分析を勉強するのにオススメな本を以下にまとめておきます。
■多変量解析入門
回帰分析・判別分析をはじめとした様々な手法が体系的にまとまっています。非常に分かりやすくまとめてあるので初学者にも優しく、そしてある程度勉強した上での復習としても非常に有用な書籍になっています。
■回帰分析入門: Rで学ぶ最新データ解析
一般的な単回帰分析からポアソン回帰・ロジスティック回帰など一般化線形回帰モデルまで回帰に関する内容を網羅しています。Rによる実践例と共に話が進んでいくので手を動かしながら学びましょう。
より高度な手法について学ぶ理論立って学ぶことが可能です。
回帰分析まわりの手法についてオススメな本をこちらにまとめていますので良ければご覧ください!


























