スパース推定とは？理論とオススメ本を紹介！

スパース推定は、変数が非常に多い高次元データを扱う上で非常に有用な手法です。

そんなスパース推定について見ていきましょう！

予備知識として、このページを見る前に正則化についてまとめている以下のページを見ていただけるとより理解が深まると思います。

正則化正則化手法についてざっくりと説明していきます。

以下のYouTube動画でも解説していますので、あわせてチェックしてみてください！

スパースとは何か？

スパースとは、日本語で「疎」という意味。

スパース推定とは「パラメータに0が多くなるように推定すること」です。

それが何の役に立つのでしょう？

世の中のデータを解析するときにはパラメータは0と推定したいことが多くあります。

例えば、回帰に置ける回帰係数の推定で便利です。

説明変数が多い場合に目的変数に関係ない説明変数への係数は0と推定したいです。

このとき通常通りに最小二乗法を行い、AICなどの基準によって変数選択を行っても良いのですが、サンプルサイズよりパラメータが多い場合にはそもそも解析できないということがあります。

そんなときに、スパース推定をすることで回帰係数の推定と変数選択を同時に行うことができるという利点があります（この手法はLassoと呼ばれます）。

他にも、主成分分析の際に出てくるローディングベクトルのスパース推定や、精度行列のスパース推定など応用範囲はとても広いです。

真のモデルでは0となっているべきところが得られた標本からでは誤差によって通常では0と推定されないところを効率的に0と推定してくれるところが強みです。

では、具体的に式を交えて例を見ていきます。

スパース推定の例：Lasso（ラッソ）

”正則化”の記事では、Graphical Lassoという手法を少し紹介しましたが、ここで改めてLassoという手法について説明します。

Lasso（Least absolute selection and shrinkage operator）とは正則化項を利用することで回帰係数をスパースに推定できる手法です。

回帰係数がスパース、すなわちいくつかの要素が０になるということは推定と同時に変数選択されているということになります。

通常の最小二乗法に$L_1$型の正則化項を加えた式を最適化することでLassoの推定量が得られます。式は次のようになります。
$\displaystyle \|{\bf y}-{\bf X}{\bf \beta}\|_2^2+\lambda\|{\bf \beta}\|_1$
これはRidge回帰の式に似ています。正則化項が$L_1$ノルムか$L_2$の違いです。ではLassoとRidgeがどのように違うかを図でイメージして見ます。

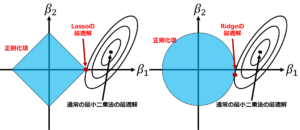
図：Lasso（左）とRdige（右）

$L_2$正則化であるRidgeの方は最適解のところでも$\beta_2$の値が残っています。一方で、$L_1$正則化であるLassoの方は最適解のところで$\beta_2$が０になっています。よってLassoを用いると推定量が得られると同時に変数選択をすることが出来ました。

Lassoの有用性として、一つの例としては、サンプルサイズより説明変数が多い場合があります。

通常の最小二乗法では多重共線性の問題で解析出来ません。

また、Ridgeでは解析が出来ても全ての値が残るので解釈が大変です。

そんなときにLassoを用いると回帰係数をスパースに推定してくれるので残る値の数も少ないので解釈も楽になります。

上でも述べたのですがスパース主成分分析やグラフィカル・ラッソなどスパース推定を利用した手法は多く提案されています。

興味があればさらに調べてみると面白いです。

スパース推定を勉強するのにオススメの本

おすすめの書籍はこちら！

この３冊で理論の基礎から応用まで包括的に捉えることが出来ます！

また、こちらの記事で線形回帰とLasso・Ridgeを比較しているので実際にスパース推定の威力を見てみたい人はあわせてご覧ください！

Lasso(ラッソ)回帰・Ridge(リッジ)回帰を線形回帰と比較して実装してみよう！当サイト【スタビジ】の本記事では、線形回帰・Lasso(ラッソ)回帰・Ridge(リッジ)回帰についてRでの実装も行いながらまとめていきます。高次元データを分析する際はぜひLasso(ラッソ)回帰・Ridge(リッジ)回帰を利用してみてくださいね！