選択バイアス(セレクションバイアス)を分かりやすく解説!どんな種類がある?

こんにちは!データサイエンティストのウマたん(@statistics1012)です。
ビジネスシーンや研究など様々なシーンで因果関係を求めたい時ってよくありますよね?
そんな時に生じる問題として有名なのが選択バイアス。
この記事では選択バイアスについて解説し、選択バイアスを極力避ける方法についても見ていきます。
ちなみに選択バイアスに対処するための統計的因果推論のアプローチについて詳しく知りたい方は以下の私のUdemy講座で学べますのでチェックしてみてください!
【初心者向け】統計的因果推論を学びPythonで実装していこう!RCT・層別解析・マッチング法・傾向スコアを学ぼう!
| 【時間】 | 3.5時間 |
|---|---|
| 【レベル】 | 初級 |
統計的因果推論について詳しく知りたいならこのコース!
今なら購入時に「J56MYR9S」という講師クーポンコードを入れると90%オフ以上の割引価格になりますのでぜひご受講ください!
それでは見ていきましょう!
目次
選択バイアス(セレクションバイアス)とは?
選択バイアス(セレクションバイアス)とは、因果関係を確かめるために対象となる集団をピックアップする際に起きてしまうバイアスのことです。
選択バイアスに気を付けないと、何もない事象に対して因果関係を作り出してしまったり、実際には因果効果があるのにないように見えることがあったりします。
何も考えずに調査や分析を設計してしまうと、実は選択バイアスが働いていて何の意味もない実験になっている危険性があるので注意しましょう。
それではどんな選択バイアスが存在するのかいくつか種類を見ていきましょう!
選択バイアス(セレクションバイアス)に関しては以下のYouTube動画でも解説していますので合わせてチェックしてみてください!
選択バイアス(セレクションバイアス)の種類
選択バイアス(セレクションバイアス)には色んな種類があります。
それぞれの特徴を理解して、罠に陥らないように注意しましょう!
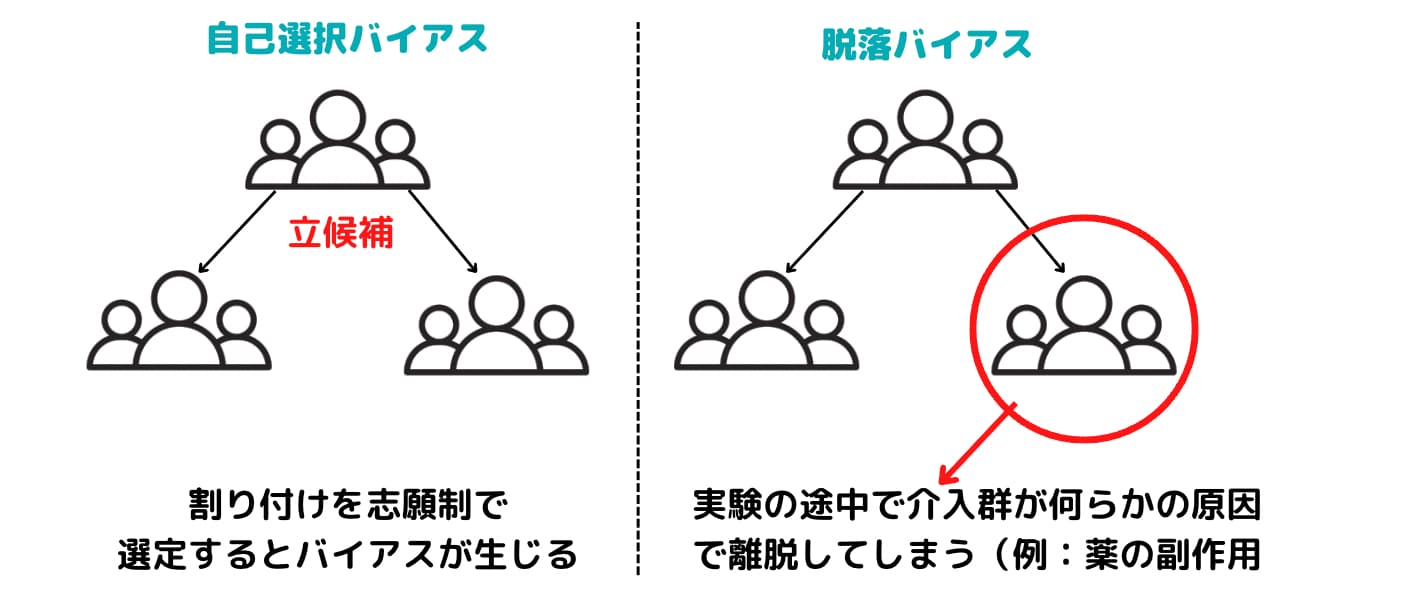
自己選択バイアス
まず1つ目が自己選択バイアスです。
たとえば、タバコと健康の因果関係を調査するためにタバコを吸っている人で健康調査に協力してくれる人に募集をかけたとします。
この時、調査に協力してくれる人は健康に自信のある人かもしれませんし、最近調子が悪く健康調査をしておきたい人かもしれません。
この場合、調査に対する志願者に何らかのバイアスが生じてしまっているため正しい因果関係を見出すことが難しくなる傾向にあります。
志願者バイアスということもあります。
生存者バイアス
続いて生存者バイアスです。
特定の新薬の効果を確かめるためにランダムに分けた2つの集団に対して片方に新薬投与をしたとします。
しかし新薬の副作用で多くの人が体調を崩し調査に参加できなくなってしまった場合、残った集団で比較しても正しい因果関係は分からない可能性があります。
このようなバイアスを生存者バイアスと言います。脱落バイアスということもあります。
何気ないアンケートに潜む選択バイアス
世の中に出回っている多くの調査には少なからず選択バイアスが生じています。
世論調査を電話で実施している場合やサービスのコンセプト調査を特定のSNSだけを通して行う場合など最初からターゲットとなる対象に選択のバイアスがかかってしまっているのは言わずもがなでしょう。
最近だと固定電話を持っている世帯は少なくなっており、若い人ほど固定電話を家に持っていない傾向が強いと思います。
その結果、固定電話を使った調査では年齢層の高い層にバイアスがかかった結果が得られてしまう可能性が高いです。
それを全国民の総意の結果として出してしまうのは危険性が高いでしょう。
選択バイアスの存在を意識しながら世に出回っている調査結果を眺めてみると面白いです。
世の中には多くの選択バイアスが隠れています。
因果関係を紐解く際には選択バイアスの存在に注意しましょう。
選択バイアスの回避方法・対処方法
それでは選択バイアスを回避・対処するにはどうすればよいでしょうか?
まずできる限り、調査の事前設計時に選択バイアスを回避できるように注意すること。
そこで登場するのがランダム化比較実験(RCT)というアプローチ。
非常にシンプルで調査の対象を完全にランダムにピックアップする・割り付けるというもの。
ランダム化比較実験について詳しくは以下の記事でまとめています!

しかし、このランダム化比較実験ができればそれに越したことはないのですが、既に調査設計を誤って実行してしまった場合や、倫理的に不可能な場合もあります。
例えば、タバコと肺がんの関係を調べるために、ランダムに割り付けた人々に一日10本のタバコを吸ってもらい肺がんになるまで実験するというのは倫理的に不可能です。
さて、このような場合はどうすればよいでしょうか?
そこで登場するのが統計的因果推論の様々なアプローチです。
色んなアプローチがあるので、詳しくはぜひ以下の記事を見てほしいのですが、実際にどのようにバイアスに対処して真の因果効果を推定していくか例を見ていきましょう!

ここでは、今回は血圧を下げるサプリの効果があるのかないのか確かめるケースを考えてみます。
まず、血圧を下げるサプリを試したい人を公募で募集し、彼らに血圧を下げるサプリを試して、それをサプリを摂取していない一般人と比較しました。
そう、そもそも年齢が高く血圧が高い人ほど血圧を下げるサプリを飲みたいと思い応募してきている可能性が高く、比較対象には年齢という交絡因子が存在することが考えられます。
こちらはまさに先ほど紹介した自己選択バイアスにはまっていることが分かるでしょう。
この選択バイアスが生じている実験設定をそのままPythonコードに落とし込んでいきましょう!
# --- データ生成 ---
N_obs = 1000
Age_obs = np.random.normal(50, 10, size=N_obs)
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# 年齢が高いほどサプリを飲みやすい
p_supp_obs = sigmoid(0.3 * (Age_obs - 50))
Supplement_obs = np.random.binomial(1, p_supp_obs)
BloodPressure_obs = 130 + 0.3*Age_obs - 4.0*Supplement_obs + np.random.normal(0, 5, size=N_obs)
df_obs = pd.DataFrame({
'Age': Age_obs,
'Supplement': Supplement_obs,
'BloodPressure': BloodPressure_obs
})
# --- まずは「年齢を無視」して単純比較 ---
mean_bp_supp_obs = df_obs[df_obs['Supplement'] == 1]['BloodPressure'].mean()
mean_bp_nosupp_obs = df_obs[df_obs['Supplement'] == 0]['BloodPressure'].mean()
diff_obs_naive = mean_bp_supp_obs - mean_bp_nosupp_obs
print(f"サプリ群 平均血圧: {mean_bp_supp_obs:.2f}")
print(f"非サプリ群 平均血圧: {mean_bp_nosupp_obs:.2f}")
print(f"単純比較(サプリ - 非サプリ): {diff_obs_naive:.2f} ")
課題設定に沿って、1000人を対象に年齢が高いほどサプリを飲みやすいというような条件設定にしています。
結果は以下のようになりました。
サプリ群 平均血圧: 143.04
非サプリ群 平均血圧: 143.06
単純比較(サプリ – 非サプリ): -0.02
本来であればサプリの効果があるはずなのに、ほぼ差がないことが分かります(※今回サプリを飲んでいるか否かで4.0を足しているので、本来であれば単純比較の差が4近くなるはず)。
さて、この選択バイアスを対処するために層別解析というアプローチを使ってみます。
今回、年齢という交絡因子が原因で自己選択バイアスがはたらいていました。
それでは、この年齢という交絡因子の影響をなくして差を比較すればよいのです。
例えば、年齢を〜20代、30代、40代、50代〜みたいな感じで分けて、それぞれのグループ内で比較してあげれば、年齢による影響は極力小さくなります。
このようなアプローチを層別解析と呼ぶのです。
では実際にPythonコードに落とし込んでいきましょう!
# 年齢を4分割して層を作り、それぞれの層で
# (サプリあり vs なし) の平均差を求め、最後に加重平均をとる。
df_obs['Age_bin'] = pd.qcut(df_obs['Age'], q=4, labels=False)
strata_effects = []
strata_sizes = []
for bin_label in sorted(df_obs['Age_bin'].unique()):
subset = df_obs[df_obs['Age_bin'] == bin_label]
mean_bp_supp_stratum = subset[subset['Supplement']==1]['BloodPressure'].mean()
mean_bp_nosupp_stratum = subset[subset['Supplement']==0]['BloodPressure'].mean()
# サプリ - 非サプリ
effect = mean_bp_supp_stratum - mean_bp_nosupp_stratum
strata_effects.append(effect)
strata_sizes.append(len(subset))
weights = np.array(strata_sizes) / np.sum(strata_sizes)
overall_effect_strat = np.sum(np.array(strata_effects) * weights)
for i, e in enumerate(strata_effects):
print(f"層 {i} の効果(サプリ - 非サプリ): {e:.2f} (サンプル数={strata_sizes[i]})")
print(f"層別加重平均(サプリ - 非サプリ): {overall_effect_strat:.2f} (ちゃんと効果が出る)")グループを年齢によって4つに分けてそれぞれにおいてサプリ摂取層と非摂取層を比較し、最終的に加重平均を取っています。
結果は以下のようになりました。
層 0 の効果(サプリ – 非サプリ): -1.25 (サンプル数=250)
層 1 の効果(サプリ – 非サプリ): -4.72 (サンプル数=250)
層 2 の効果(サプリ – 非サプリ): -3.11 (サンプル数=250)
層 3 の効果(サプリ – 非サプリ): -4.67 (サンプル数=250)
層別加重平均(サプリ – 非サプリ): -3.43
真のサプリの効果が-4なので、ちゃんと真のサプリの効果に近づいていることが分かりますね!
層別解析に関してもっと詳しくは以下の記事をチェックしてみてください!

選択バイアス(セレクションバイアス) まとめ
ここまでで、因果効果を確かめる上で注意しておきたい選択バイアスの種類や対処方法について解説してきました。
非常に重要な概念なので、必ず理解しておきましょう!
ちなみに、冒頭でもお伝えしましたが、選択バイアスに対処するための統計的因果推論のアプローチについて詳しく知りたい方は以下の私のUdemy講座で学べますのでチェックしてみてください!
【初心者向け】統計的因果推論を学びPythonで実装していこう!RCT・層別解析・マッチング法・傾向スコアを学ぼう!

| 【時間】 | 3.5時間 |
|---|---|
| 【レベル】 | 初級 |
統計的因果推論について詳しく知りたいならこのコース!
今なら購入時に「J56MYR9S」という講師クーポンコードを入れると90%オフ以上の割引価格になりますのでぜひご受講ください!
また、さらに詳しくAIやデータサイエンスの勉強がしたい!という方は当サイト「スタビジ」が提供するスタビジアカデミーというサービスで体系的に学ぶことが可能ですので是非参考にしてみてください!
AIデータサイエンス特化スクール「スタアカ」

| 【価格】 | ライトプラン:1280円/月 プレミアムプラン:149,800円 |
|---|---|
| 【オススメ度】 | |
| 【サポート体制】 | |
| 【受講形式】 | オンライン形式 |
| 【学習範囲】 | データサイエンスを網羅的に学ぶ 実践的なビジネスフレームワークを学ぶ SQLとPythonを組み合わせて実データを使った様々なワークを行う マーケティングの実行プラン策定 マーケティングとデータ分析の掛け合わせで集客マネタイズ |
データサイエンティストとしての自分の経験をふまえてエッセンスを詰め込んだのがこちらのスタビジアカデミー、略して「スタアカ」!!
当メディアが運営するスクールです。
24時間以内の質問対応と現役データサイエンティストによる複数回のメンタリングを実施します!
カリキュラム自体は、他のスクールと比較して圧倒的に良い自信があるのでぜひ受講してみてください!
他のスクールのカリキュラムはPythonでの機械学習実装だけに焦点が当たっているものが多く、実務に即した内容になっていないものが多いです。
そんな課題感に対して、実務で使うことの多いSQLや機械学習のビジネス導入プロセスの理解なども合わせて学べるボリューム満点のコースになっています!
Pythonが初めての人でも学べるようなカリキュラムにしておりますので是非チェックしてみてください!
ウォルマートのデータを使って商品の予測分析をしたり、実務で使うことの多いGoogleプロダクトのBigQueryを使って投球分析をしたり、データサイエンティストに必要なビジネス・マーケティングの基礎を学んでマーケティングプランを作ってもらったり・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践してもらったりする盛りだくさんの内容になってます!
・BigQuery上でSQL、Google Colab上でPythonを使い野球の投球分析
・世界最大手小売企業のウォルマートの実データを用いた需要予測
・ビジネス・マーケティングの基礎を学んで実際の企業を題材にしたマーケティングプランの策定
・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践して稼ぐ






















