こんにちは！データサイエンティストのウマたん(@statistics1012)です。
統計的因果推論とは変数間の因果関係をデータから明らかにしようという分野。
この分野は大きく二つの枠組みに分けられます。
■一つ目は、変数間の因果構造を既知として出発し、介入したときの因果効果を推定する問題
■二つ目は、変数間の因果構造を未知として出発し、観測されているデータから因果構造を導く問題
ほとんどの場合、統計的因果推論というと一つ目に言及しているものが多いです。
また、二つ目の内容は特に統計的因果探索と呼ばれます。
この記事では主に一つ目の方法について紹介して、最後に少し二つ目の方法についても触れたいと思います。
ちなみに、統計的因果推論について詳しく知りたい方は以下の私のUdemy講座で学べますのでチェックしてみてください！
【初心者向け】統計的因果推論を学びPythonで実装していこう！RCT・層別解析・マッチング法・傾向スコアを学ぼう！
| 【時間】 | 3.5時間 |
|---|---|
| 【レベル】 | 初級 |
統計的因果推論について詳しく知りたいならこのコース！
今なら購入時に「T5FVH5RN296K」という講師クーポンコードを入れると90%オフ以上の割引価格になりますのでぜひご受講ください！
目次
相関関係と因果関係
例えば、「年収と一日の平均摂取カロリーには負の相関関係がある」
と聞いたらみなさんはどのように思いますか？
「よっしゃ！年収をあげるためにカロリーを抑えよう！」と思うでしょうか？
でも実際にはカロリーを低く抑えることによって年収が上がるということは期待されません。
なぜなら相関関係があったとしても因果関係があるとは限らないからです。
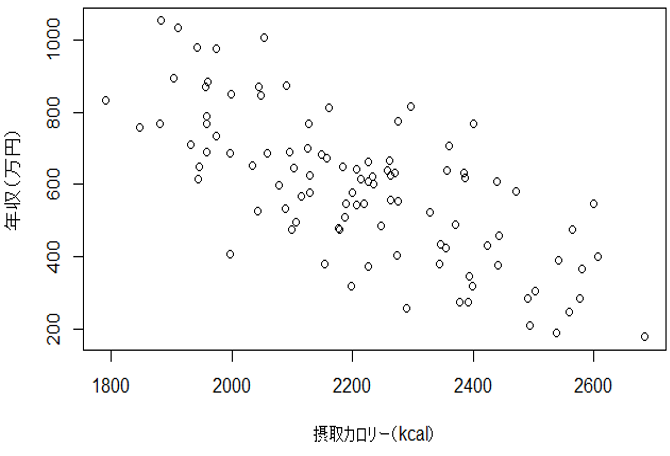
図1. 年収と摂取カロリーの散布図（仮想データ）
さて、先ほどの「年収と一日の摂取カロリー」には相関関係があることは間違いないです。
しかし、経験的に一日の摂取カロリーを低くしても年収が上がるという因果関係は認められないと思います。
それではなぜ「年収」と「摂取カロリー」の間に相関関係が見られたのでしょうか？
それは、「年収」と「摂取カロリー」の裏に「年齢」という隠れた因子が存在するからです。
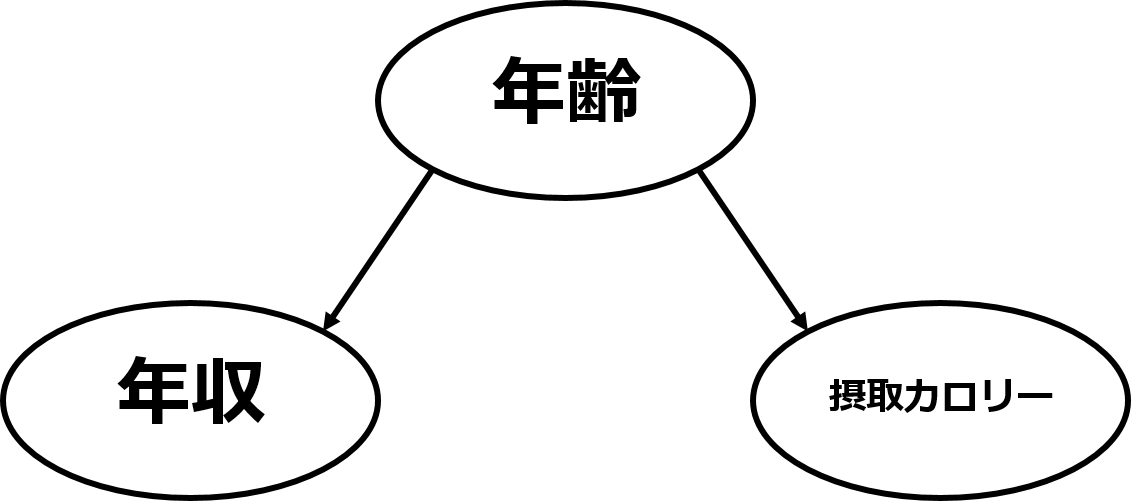
図2. 交絡した因果グラフ
一般的に年齢が高くなると年収は上がります。そして年齢が高くなると摂取カロリーは低くなるでしょう。
そのため摂取カロリーが低い人ほど年収が高くなったのです。
このような変数間の構造のことを交絡と呼びます。
また、交絡しているときの相関を擬似相関（偽相関）と呼びます。
大事なのは相関関係があっても因果関係があるとは限らないということです。
統計的因果推論の種類
相関と因果は同じものではないと述べました。
改めて因果関係についてまとめておきます。
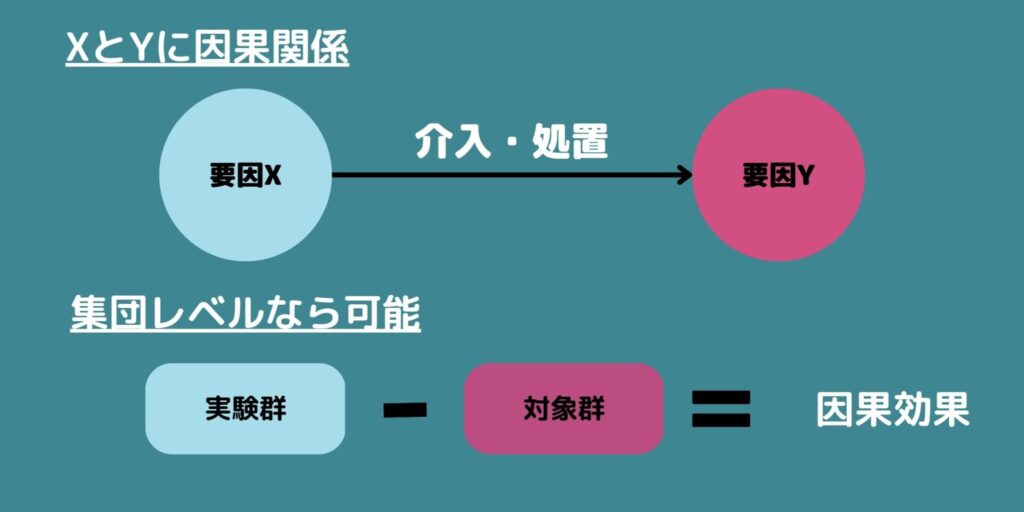
要因Xと要因Yがあるとします。
「要因Xを変化させたときに要因Yも変化する場合、XとYには因果関係がある」と言います。
この「変化させる」ことを介入・処置などと呼びます。
また、因果関係の強さ、つまりXを変化させたときにどれくらいYが変化するのかを表したものを因果効果と呼びます。
では因果効果はデータからどのように求めれば良いでしょうか？
因果効果は「同じ対象が介入を受けた場合と受けなかった場合の結果の差」と定義されます。
例えば、血圧を下げると期待される新薬があった場合、あるAさんに新薬を飲んでもらった場合とただのビタミン剤を飲んでもらった場合を比較すれば個人レベルの因果効果を正しく推定出来ます。
しかし、同じ人に二通りのことをやってもらうのはタイムスリップでも出来ない限り不可能です。
このように「もし飲んでいたら（飲んでいなかったら）」と考えることを反事実モデルと呼びます。
ここから反事実モデルにおいて因果効果をどうやって推定していくかを見ていきましょう。
ランダム化比較実験
結論から言って個人レベルの因果効果を推定することは一般には不可能です。
しかし集団レベルの因果効果であれば方法はいくつかあります。
ある集団を新薬を飲んでもらう群（実験群・介入群・処置群などと呼ぶ）とビタミン剤を飲んでもらう群（対照群・統制群・コントロール群などと呼ぶ）に分けて、結果の差を見ます
集団の中のそれぞれの対象が介入群と対照群のどちらになるかを決定させることを割り付けと呼びます。
では、集団をどのように割り付ければ良いでしょうか。
例えば、男性なら新薬を飲んでもらい、女性ならビタミン剤を飲んでもらうという割り付けをしてみます。
すると、確かに結果の差を得ることは出来ますが、果たしてそれは新薬の効果によるものなのでしょうか。性別に由来する影響かもしれません。
この場合、性別が交絡因子となっています。このように割り付けも適切に行わないと交絡を引き起こしてしまいます。
結局、如何にして交絡に対処するかが重要ということです。
因果効果を測定するには交絡因子を調整する必要があります。
最も最適な方法は実験研究という方法です。
実験研究とは、割り付けを完全にランダムに行う方法でありランダム化比較実験（Randomized Controlled Trial;RCT）と呼ばれます。
RCTでは例えば、一人一人にコインを投げてもらい表なら介入群、裏なら対照群とします。
これによって、いろんな潜在的な交絡因子があっても二つの群の分布は平均的に等しくなることが期待されます。
したがって、介入群と対照群の結果の差は介入によるものであると結論づけることが出来ます。
ランダム化比較実験（RCT）をPythonで実装してみよう！
さて、それではこのRCTをPythonで実装してみましょう！
今回は血圧を下げるサプリの効果があるのかないのか確かめるケースを考えてみます。
まず、血圧を下げるサプリを試したい人を公募で募集し、彼らに血圧を下げるサプリを試して、それをサプリを摂取していない一般人と比較しました。
そう、そもそも年齢が高く血圧が高い人ほど血圧を下げるサプリを飲みたいと思い応募してきている可能性が高く、比較対象には年齢という交絡因子が存在することが考えられます。
この誤った実験設定をそのままPythonコードに落とし込んでいきましょう！
# --- データ生成 ---
N_obs = 1000
Age_obs = np.random.normal(50, 10, size=N_obs)
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# 年齢が高いほどサプリを飲みやすい
p_supp_obs = sigmoid(0.3 * (Age_obs - 50))
Supplement_obs = np.random.binomial(1, p_supp_obs)
BloodPressure_obs = 130 + 0.3*Age_obs - 4.0*Supplement_obs + np.random.normal(0, 5, size=N_obs)
df_obs = pd.DataFrame({
'Age': Age_obs,
'Supplement': Supplement_obs,
'BloodPressure': BloodPressure_obs
})
# --- まずは「年齢を無視」して単純比較 ---
mean_bp_supp_obs = df_obs[df_obs['Supplement'] == 1]['BloodPressure'].mean()
mean_bp_nosupp_obs = df_obs[df_obs['Supplement'] == 0]['BloodPressure'].mean()
diff_obs_naive = mean_bp_supp_obs - mean_bp_nosupp_obs
print(f"サプリ群 平均血圧: {mean_bp_supp_obs:.2f}")
print(f"非サプリ群 平均血圧: {mean_bp_nosupp_obs:.2f}")
print(f"単純比較(サプリ - 非サプリ): {diff_obs_naive:.2f} ")
課題設定に沿って、1000人を対象に年齢が高いほどサプリを飲みやすいというような条件設定にしています。
結果は以下のようになりました。
サプリ群 平均血圧: 143.04
非サプリ群 平均血圧: 143.06
単純比較(サプリ – 非サプリ): -0.02
本来であればサプリの効果があるはずなのに、ほぼ差がないことが分かります（※今回サプリを飲んでいるか否かで4.0を足しているので、本来であれば単純比較の差が4近くなるはず）。
それでは続いて、ランダム化比較実験（RCT）を用いて割り付けをおこなっていきましょう！
Pythonコードは以下になります。
# --- データ生成 ---
N_rct = 1000
Age_rct = np.random.normal(50, 10, size=N_rct)
# サプリ割付：RCTなので年齢関係なく50%割付
Supplement_rct = np.random.binomial(1, 0.5, size=N_rct)
BloodPressure_rct = 130 + 0.3*Age_rct - 4.0*Supplement_rct + np.random.normal(0, 5, size=N_rct)
df_rct = pd.DataFrame({
'Age': Age_rct,
'Supplement': Supplement_rct,
'BloodPressure': BloodPressure_rct
})
# --- 単純比較 ---
mean_bp_supp = df_rct[df_rct['Supplement'] == 1]['BloodPressure'].mean()
mean_bp_nosupp = df_rct[df_rct['Supplement'] == 0]['BloodPressure'].mean()
diff_rct = mean_bp_supp - mean_bp_nosupp
print(f"サプリ群 平均血圧: {mean_bp_supp:.2f}")
print(f"非サプリ群 平均血圧: {mean_bp_nosupp:.2f}")
print(f"単純比較(サプリ - 非サプリ): {diff_rct:.2f} (ちゃんと効果が出る)")
今回は年齢の関係なくランダムに割り付けをおこなっています。
結果は以下のようになりました。
サプリ群 平均血圧: 140.82
非サプリ群 平均血圧: 145.12
単純比較(サプリ – 非サプリ): -4.29 (ちゃんと効果が出る)
ちゃんとサプリ群の方が4近く血圧が小さくなっており、効果が出ていることが分かりますね！
ランダム化比較実験（RCT）に関して詳しくは以下の記事で解説していますのでチェックしてみてください！
ただ割り付けをランダムにすれば良いRCTは使い勝手が良さそうに見えますが、デメリットもあります。
そもそもそのような実験ができれば良いが、ランダムな割り付けが出来ない場合も多いのです
例えば、タバコと肺がんの関係を調べるために、ランダムに割り付けた人々に一日１０本のタバコを吸ってもらい肺がんになるまで実験するというのは倫理的に不可能です。
また、コストの問題もありますし、そもそもすでにデータが得られている場合にはどうしようもありません。
実験研究とは異なり割り付けがランダム化されていない方法は観察研究と呼ばれます。
現実問題では、観察データが多いこともあるので次からは観察データにおける交絡因子への対処方法を紹介していきます。
層別解析
一つ目は、層別解析という方法です。
少し前の「年収と一日の摂取カロリー」というデータを考えて見ましょう。
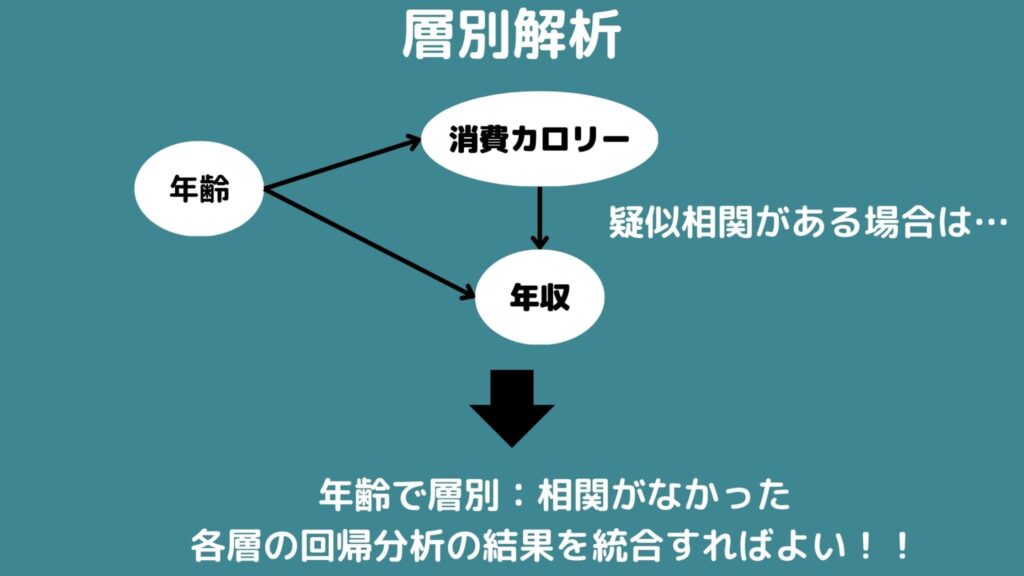
年収と摂取カロリーの二つの上流には年齢という交絡因子が存在するために疑似相関が現れてしまいました。
そこで、例えば、20代・30代・40代・50代・60代以上で層別化してみるとそれぞれ層の中のデータでは相関はないことがわかります。
もし、層別して交絡因子を取り除いても原因変数と結果変数に直接的な因果関係があれば各層の中で単回帰分析を行い、各層での回帰係数を統合することで因果効果を推定することが出来ます。
しかし、この方法にもデメリットがあり層別するとサンプルサイズが減るので各層での推定が不安定になります。
また、交絡因子が連続変量の場合には離散化して層別するのですが、離散化には解析者の恣意性が入ってしまうことも課題として挙げられます。
さらに、測定されていない交絡因子に対しては対処が出来ません。
層別解析をPythonで実装！
それでは層別解析をPythonで実装する方法について見ていきましょう！
先ほどRCTを実施した例と同様のケースを考えます。
以下のようにコードを書いてみましょう！
# 年齢を4分割して層を作り、それぞれの層で
# (サプリあり vs なし) の平均差を求め、最後に加重平均をとる。
df_obs['Age_bin'] = pd.qcut(df_obs['Age'], q=4, labels=False)
strata_effects = []
strata_sizes = []
for bin_label in sorted(df_obs['Age_bin'].unique()):
subset = df_obs[df_obs['Age_bin'] == bin_label]
mean_bp_supp_stratum = subset[subset['Supplement']==1]['BloodPressure'].mean()
mean_bp_nosupp_stratum = subset[subset['Supplement']==0]['BloodPressure'].mean()
# サプリ - 非サプリ
effect = mean_bp_supp_stratum - mean_bp_nosupp_stratum
strata_effects.append(effect)
strata_sizes.append(len(subset))
weights = np.array(strata_sizes) / np.sum(strata_sizes)
overall_effect_strat = np.sum(np.array(strata_effects) * weights)
for i, e in enumerate(strata_effects):
print(f"層 {i} の効果(サプリ - 非サプリ): {e:.2f} (サンプル数={strata_sizes[i]})")
print(f"層別加重平均(サプリ - 非サプリ): {overall_effect_strat:.2f} (ちゃんと効果が出る)")グループを年齢によって4つに分けてそれぞれにおいてサプリ摂取層と非摂取層を比較し、最終的に加重平均を取っています。
結果は以下のようになりました。
層 0 の効果(サプリ – 非サプリ): -1.25 (サンプル数=250)
層 1 の効果(サプリ – 非サプリ): -4.72 (サンプル数=250)
層 2 の効果(サプリ – 非サプリ): -3.11 (サンプル数=250)
層 3 の効果(サプリ – 非サプリ): -4.67 (サンプル数=250)
層別加重平均(サプリ – 非サプリ): -3.43
ちゃんとサプリの効果が出ていることが分かりますね！
層別解析に関してもっと詳しくは以下の記事をチェックしてみてください！
回帰モデルの利用
次に、回帰モデルの利用について紹介します。
この方法は結果変数を目的変数に、原因変数と交絡因子を説明変数にして回帰分析をする方法です。
回帰分析を行った場合でのある変数の偏回帰係数は他の変数を固定した場合のその変数が一単位変化したときの目的変数の変化量を表しているのでそのまま因果効果として考えられます。
ただ説明変数に入れる因子を選択する際には注意が必要であり、間違えると偏回帰係数にバイアスがかかってしまいます。
どの変数を説明変数に入れれば良いかはバックドア基準で決定すると良いです。
デメリットとしては仮定した回帰モデルが真のモデルと乖離している場合には正しい推定を行うことが出来ません。
そして、交絡因子が多くなればモデルが乖離する可能性が高くなります。
Pythonで回帰分析を実装してみよう！
それでは今回のケースを用いて、Pythonで回帰分析を実装してみましょう！
以下のようにPythonコードを書いてみましょう！
# 単回帰(サプリのみ)で回帰：BloodPressure ~ Supplement
model_naive = smf.ols('BloodPressure ~ Supplement', data=df_obs).fit()
coef_naive = model_naive.params['Supplement']
# 年齢を調整したうえでサプリ効果を推定した場合
model_adjusted = smf.ols('BloodPressure ~ Supplement + Age', data=df_obs).fit()
coef_adjusted = model_adjusted.params['Supplement']
print("\n単回帰(サプリのみ)の結果:")
print(model_naive.summary())
print(f" → サプリ係数: {coef_naive:.2f}")
print("\n年齢を調整した回帰モデル ===")
print(model_adjusted.summary())
print(f" → サプリ係数: {coef_adjusted:.2f}")
年齢を入れずにサプリのみを説明変数に入れた場合と、年齢も入れた場合を比較しています。
結果的にはサプリのみの場合のサプリ係数は0.342となり、年齢も説明変数に入れた場合のサプリ係数は-4.067となりました。
ちゃんと、年齢という交絡因子を説明変数に入れて回帰分析をすることでサプリの効果を確認できたことが分かりました。
回帰分析に関しては以下の記事でまとめています。
マッチング
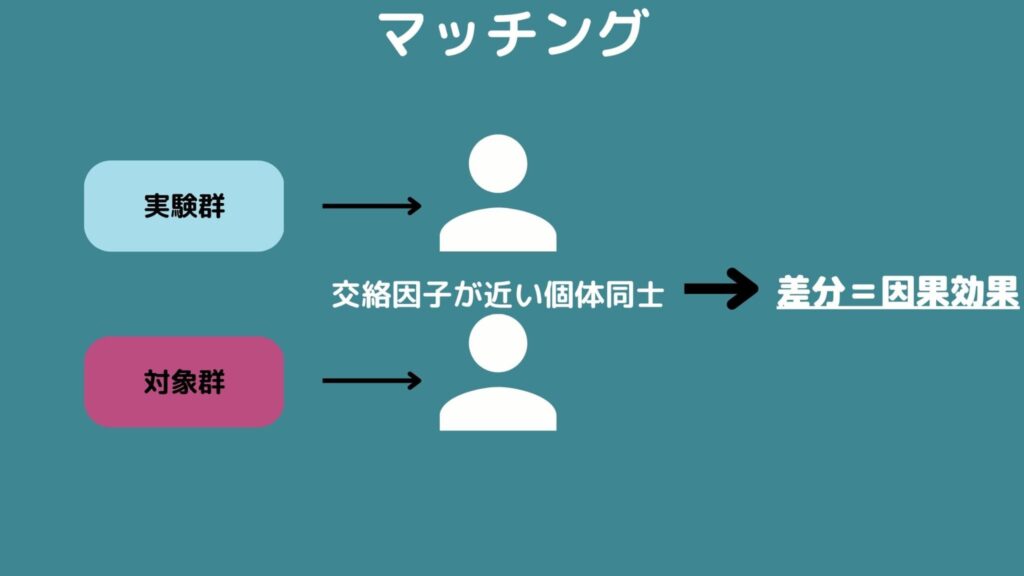
２群の間で交絡因子の値が近い個体をマッチングさせる方法です。
交絡因子が近いならその二人はほぼ同じ人とみなすことが出来るので結果の差を介入による因果効果だと考えて良いでしょうということです。
各々をマッチングして結果の差をとったらそれらを統合すれば完了です。
しかし、マッチングにも層別解析と似たデメリットがあります。
まず、交絡因子の数が多ければマッチングは難しくなります。
さらに、交絡因子が質的なら完璧にマッチングさせることも出来ますが連続変量ならば何かしらの距離を定義して近いものをマッチングする必要があります。
また、どうしてもうまくマッチング出来ない個体も出てきます。
そしてマッチング出来ない個体数は交絡因子の数が多くなると増えてデータを無駄にすることになります。
Pythonでマッチングを実装！
それではマッチングをPythonで実装していきましょう！
ここではk近傍法という手法を用いて、サプリ・非サプリ群の中で年齢の近い組み合わせを作っていきます。
以下のようにPythonコードを書いていきます。
from sklearn.neighbors import NearestNeighbors
# 観察データからサプリ群と非サプリ群を分ける
df_treated = df_obs[df_obs['Supplement'] == 1].copy()
df_control = df_obs[df_obs['Supplement'] == 0].copy()
# 最近傍マッチング: Ageを指標に
nbrs = NearestNeighbors(n_neighbors=1).fit(df_control[['Age']])
distances, indices = nbrs.kneighbors(df_treated[['Age']])
# マッチされた非サプリ群レコードを取得
matched_controls = df_control.iloc[indices.flatten()].copy()
matched_controls.index = df_treated.index
# 効果(サプリ - 非サプリ)
matched_diff = df_treated['BloodPressure'] - matched_controls['BloodPressure']
ate_matching = matched_diff.mean()
print(f"推定されたサプリ効果(サプリ - 非サプリ): {ate_matching:.2f}")k近傍法とは距離の近いサンプルを見つける手法。今回は年齢の最も近いユーザーを見つけるコードになっています。
特定のサプリユーザーに対して最も年齢の近い非サプリユーザーを探して血圧の差を取り、それを全てのユーザーに適用させた後、平均を取っています。
結果は以下のようになりました。
推定されたサプリ効果(サプリ – 非サプリ): -3.46
ちゃんとサプリの効果が見て取れますね！
傾向スコア
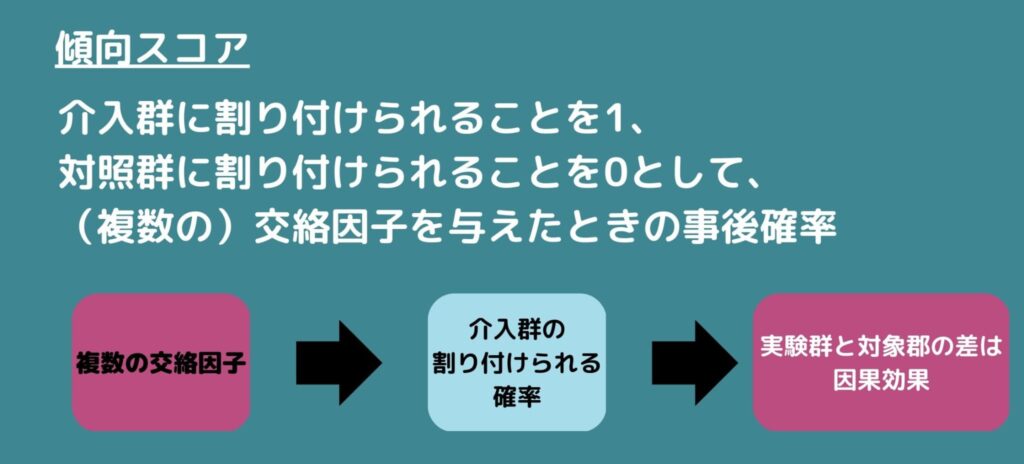
傾向スコアとは介入群に割り付けられることを1、対照群に割り付けられることを0として、（複数の）交絡因子を与えたときの事後確率のことです。
複数の交絡因子を介入群への割り付けられやすさという一変量に集約することで解析します。
事後確率の算出には一般的にロジスティック回帰かプロビット回帰が用いられますが、別に機械学習の手法でも構いません。
傾向スコアは先ほどの手法達とあわせて用いられます。
傾向スコアを区切って層別解析、傾向スコアを説明変数に入れて回帰モデルを作成、傾向スコアが近いものでマッチングなどです。
また、介入群と対照群の結果の差をバイアスなく推定するために逆確率重み付け法（Inverse Probability Weighting;IPW）や二重にロバストな方法があります。
傾向スコアにもデメリットがあり未観測の交絡因子には対応のしようがありません。
Pythonで傾向スコア算出からの逆確率重み付け法を実装！
それでは、Pythonで傾向スコアを算出してそれを元に逆確率重み付け法を実装してみましょう！
コードは以下のようになります。
# ロジスティック回帰で"Age -> Supplement"の確率を推定
lr = LogisticRegression()
lr.fit(df_obs[['Age']], df_obs['Supplement'])
df_obs['probability'] = lr.predict_proba(df_obs[['Age']])[:, 1]
# 逆確率重み(IPW)の計算
df_obs['weight'] = 0.0
df_obs.loc[df_obs['Supplement'] == 1, 'weight'] = 1.0 / df_obs.loc[df_obs['Supplement'] == 1, 'probability']
df_obs.loc[df_obs['Supplement'] == 0, 'weight'] = 1.0 / (1.0 - df_obs.loc[df_obs['Supplement'] == 0, 'probability'])
# IPWを用いたATE推定 (サプリ - 非サプリ)
df_obs['weighted_bp'] = df_obs['BloodPressure'] * df_obs['weight']
sum_wt_supp = df_obs.loc[df_obs['Supplement'] == 1, 'weight'].sum()
sum_wt_nosupp = df_obs.loc[df_obs['Supplement'] == 0, 'weight'].sum()
mean_bp_supp_weighted = df_obs.loc[df_obs['Supplement'] == 1, 'weighted_bp'].sum() / sum_wt_supp
mean_bp_nosupp_weighted = df_obs.loc[df_obs['Supplement'] == 0, 'weighted_bp'].sum() / sum_wt_nosupp
ate_ipw = mean_bp_supp_weighted - mean_bp_nosupp_weighted
print(f"推定されたサプリ効果(サプリ - 非サプリ): {ate_ipw:.2f}")
まずはじめに年齢からサプリ摂取の確率をロジスティック回帰を使って算出していきます。
そしてその確率を元に血圧に重み付けをしていきます。
サプリ摂取した人の中で、サプリ摂取確率の高い人の重みは小さくサプリ摂取確率の低い人の重みは大きく設定します。
またサプリを摂取しなかった人の中で、サプリ摂取確率の低い人の重みは小さくサプリ摂取確率の高い人の重みは大きく設定します。
そして重み付け平均を取ったものの差を取っています。
結果は以下の通りになりました。
推定されたサプリ効果(サプリ – 非サプリ): -2.58
サプリの効果が見て取れますね！
今回はシンプルに1変数を用いて傾向スコアを算出してみましたが、本来は複数の交絡変数に対して傾向スコアを算出します。
交絡変数が複数ある時は傾向スコアの採用を検討してみてください。
傾向スコアについてもっと詳しく知りたい方は以下の記事をチェックしてみてください！
回帰不連続（分断）デザイン
さて、観察データの解析はRCTと比べて交絡因子を調整しなければならないので厄介であることがわかると思います。
そんな観察データですが、実験研究に似た状況を作ることで因果効果を導く方法があり準実験と呼ばれます。
ここでは、準実験の一つである回帰不連続デザインについて説明します。
ある連続変量zで割り付けられているデータがあるとします。
そして、割り付けはあるzの値を境に完全に分断されているものとします。
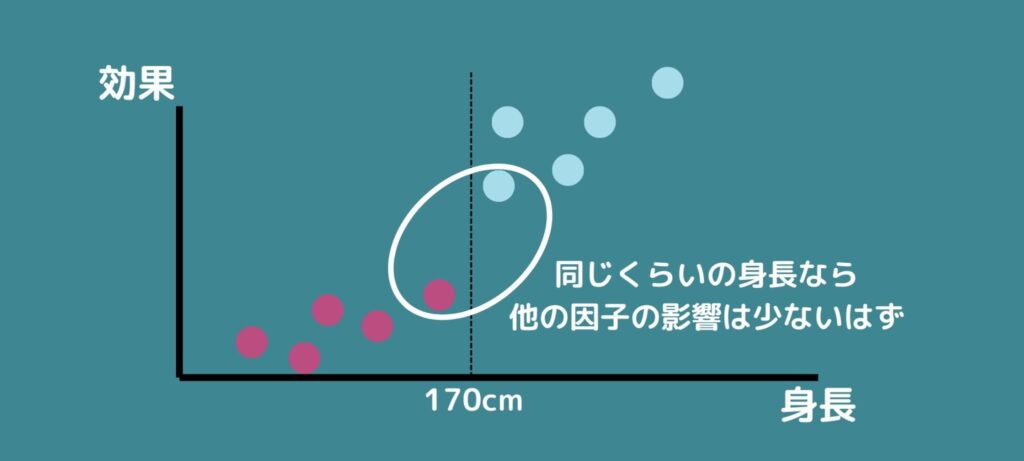
例えば、身長で割り付けをされていて介入群か対照群かの境目が170cmとしましょう。
ここで、以下の仮定をおきます。
・z=170辺りで結果変数に影響を与える他の因子が大きく変わることはない
・z=170辺りで潜在的な結果変数は連続である
つまり身長170cm付近のみなら他の因子は結果に与える影響は小さいし、出てくるであろう結果も連続的な変化で一気には変わらないようということです。
こう考えると170cmという数字に特に意味がなければ身長が169cmの人と171cmの人はほぼ同じ人だとみなせないでしょうか。
身長の測定誤差も考えると170cm付近の人々はたまたま介入群あるいは対照群に割り付けられたと考えることが出来そうです。
そこで、169cmの人と171cmの人を比較して結果に差があればそれは介入したことによる影響だということが出来ます。
この方法は仮想的にランダム化されているとみなせるので未観測の交絡因子があっても問題はありません。
また、zが時間であるものを特に中断時系列デザインと呼びます。
差の差法
次も準実験の一つである差の差法（差分の差分法）についてです。
差の差法は二つのグループに対して介入前後の二つのタイミングのデータを入手することで因果効果を推定する方法です。
例えば、ある二つの地域の店舗群を考えます。そして一方の地域の店舗群には何かの施策を打ち、もう一方には何もしないことにします。
そして介入前と後での売上高を見てみると次のような図3になったとします。この時、平行トレンド仮定と共通ショック仮定という二つの仮定が満たされていれば図3の差分(B-E)は介入による影響と考えられます。
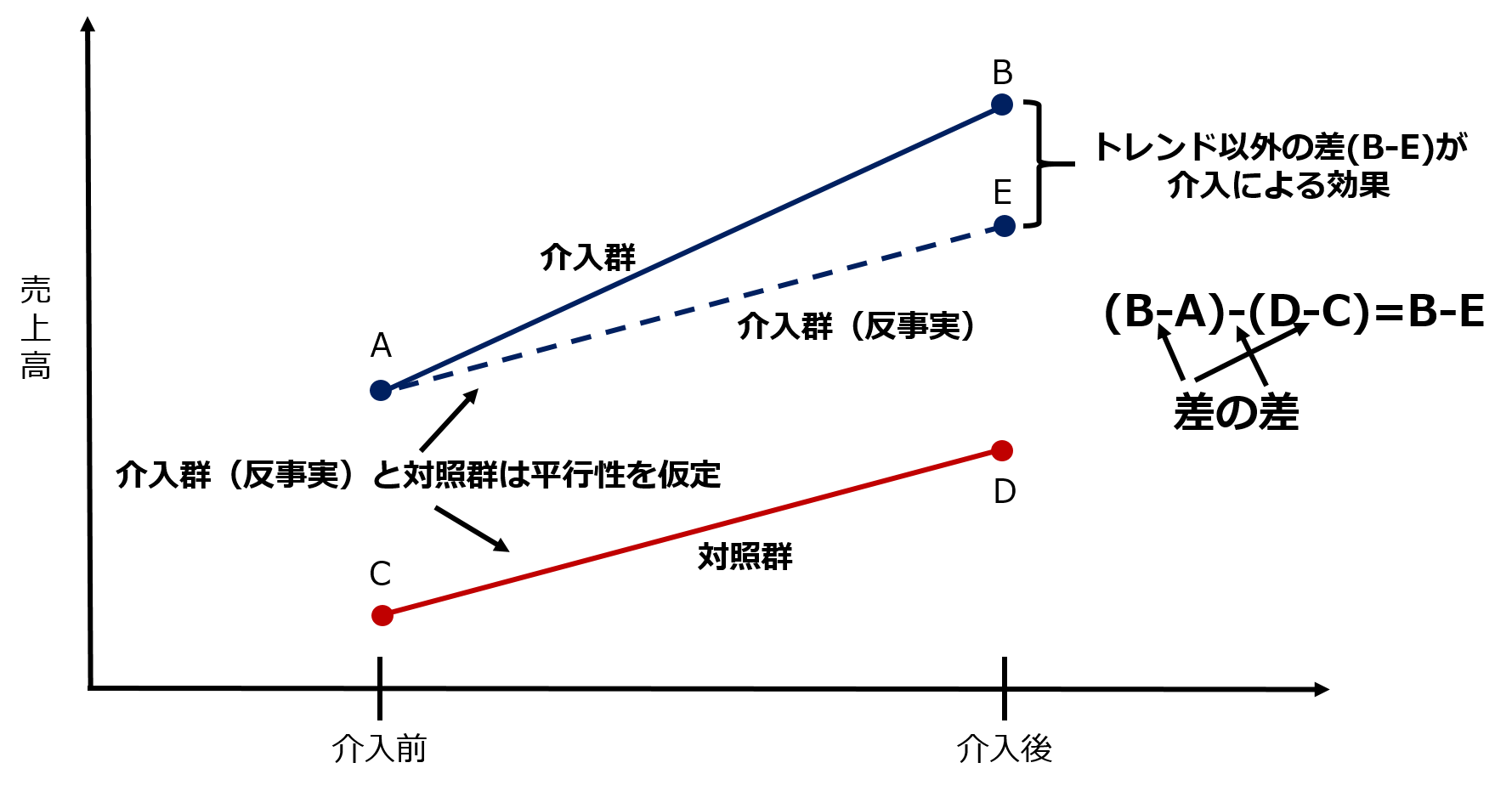図3. 差の差分析
ここで、平行トレンド仮定とは介入群と対照群でもし施策が打たれなかったら結果は平行したトレンドを描くというものです。
介入以外の影響は介入群と対照群に同等い起きているという仮定です。もし施策が打たれなかったらというのは反事実モデルでの考え方です。
また、共通ショック仮定とは介入前と介入後の間で結果に影響を与える「別のイベント」が一方の群のみに発生していないというものです。
介入以外のイベントが起きていると結果の差が介入によるものなのかそうではないのかが分からなくなってしまいます。
統計的因果探索
今までの内容は因果構造が既知であることを前提にして因果効果を推定する方法でした。
ここでは因果構造が未知の場合にデータから因果構造を推定する統計的因果探索（Causal Discovery）を紹介します。
前の「年収」、「摂取カロリー」、「年齢」の因果構造について検討してみます。
この三つの因子からなる因果構造を考えると例えば図4のようなグラフが候補の一部として考えられます。
ではデータのみからどのようにして候補を絞っていけば良いのでしょうか。
データから因果グラフの構造を定めることが可能であるにはある仮定の下で「因果グラフの構造が異なれば、観測変数の分布が必ず異なる」ことが必要です。
もし、違う構造であっても観測変数の分布が同じであればデータから構造を一意に定めることは出来ません。
図4. 因果構造の探索
因果構造の識別にはノンパラメトリック、セミパラメトリック、パラメトリックの３つのアプローチがありますが、その中で代表的なセミパラメトリックな方法であるLiNGAM(Linear non-Gaussian Acyclic Model)という手法があります。
パラメトリック手法についてはこちらの記事を参考にしてみてください！
LiNGAMは因果構造として線型性・非巡回・誤差変数が非ガウス連続分布かつ独立であることを仮定しています。
このような仮定を置くことで因果構造を一意に定めていきます。
特に、誤差変数が非ガウス連続分布というのは、ガウス分布であると平均ベクトルと共分散行列のみで分布が定められてしまい識別可能性が低くなることを回避するためです。
長くなるのでこのページではLiNGAMの詳細は省きますが、実験ではなく多くのデータを一瞬で取得出来るようになったきた現代ではデータから因果構造を探索することに価値が見出されてきています。
今はまだ手法には仮定や制約も多いですが研究の発展はめざましいものであり様々な分野での応用も期待されるでしょう。
統計的因果推論におけるセレクションバイアス
いくつかの統計的因果推論における因果効果を推定するアプローチについて見てきましたが、最後にこの分野に存在するセレクションバイアスという罠についても軽く触れておきましょう！
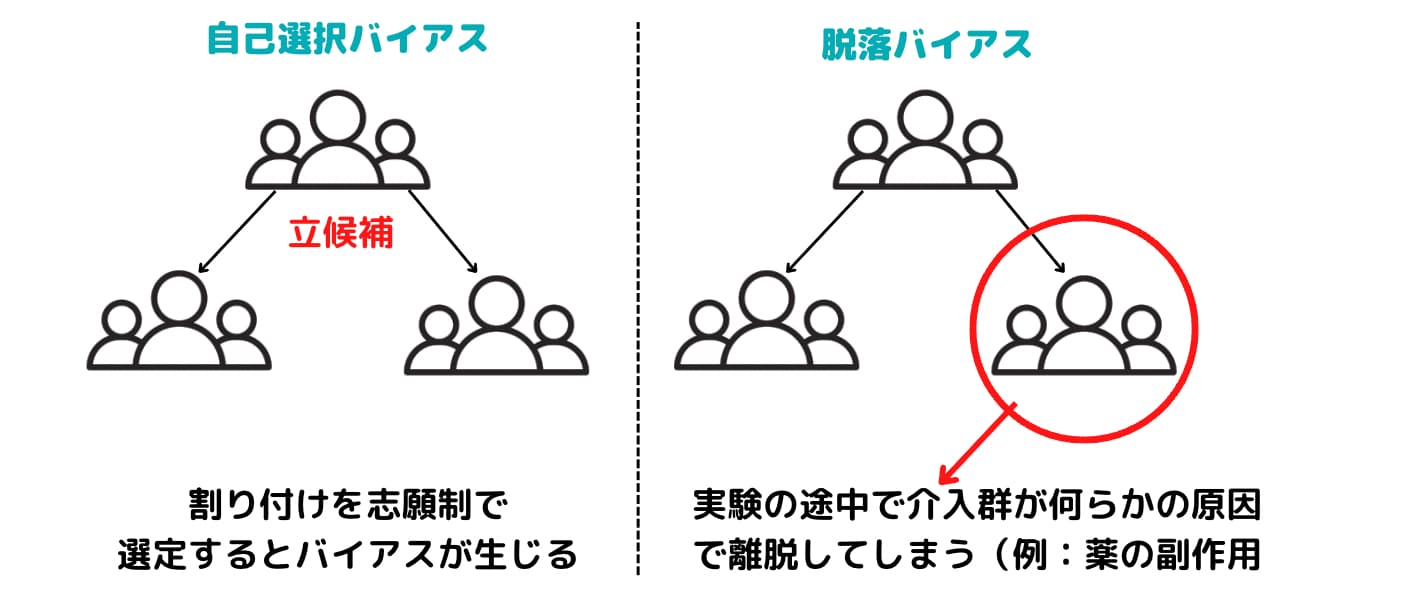
セレクションバイアスとは、因果関係を確かめるために対象となる集団をピックアップする際に起きてしまうバイアスのことです。
まさにここまで見てきたサプリの実験設定では自己選択バイアスというバイアスがはたらいています。
調査に志願してくる人に何らかのバイアスがはたらくことで、真の因果が推定できない現象です。
セレクションバイアスに気を付けないと、何もない事象に対して因果関係を作り出してしまう危険性があるので注意しましょう。
以下の記事でセレクションバイアス（選択バイアス）についてより詳しく解説していますので興味のある方はチェックしてみてください！
ちなみにセレクションバイアスに関しては以下の動画で取り上げています！
統計的因果推論 まとめ
長くなりましたが、本記事では統計的因果推論について述べてきました。最後に簡単にまとめておきましょう！
・相関関係と因果関係は必ずしも一致しない
・因果効果を推定する上で大切なのは交絡の調整
・ランダム化比較実験は交絡の影響を取り除けるが観察研究では適切に扱う必要がある
・観察データの解析として層別解析、回帰モデルの利用、マッチング、傾向スコア、回帰不連続デザイン、差の差法を紹介
・因果探索法についてLiNGAMについてちょこっと紹介
冒頭でも紹介しましたが、統計的因果推論について詳しく知りたい方は以下の私のUdemy講座で学べますのでチェックしてみてください！
【初心者向け】統計的因果推論を学びPythonで実装していこう！RCT・層別解析・マッチング法・傾向スコアを学ぼう！
| 【時間】 | 3.5時間 |
|---|---|
| 【レベル】 | 初級 |
統計的因果推論について詳しく知りたいならこのコース！
今なら購入時に「T5FVH5RN296K」という講師クーポンコードを入れると90%オフ以上の割引価格になりますのでぜひご受講ください！
また、統計的因果推論でオススメなのは以下の書籍です。
興味があれば是非読んでみてください！
・岩波データサイエンス Vol.3
・調査観察データの統計科学―因果推論・選択バイアス・データ融合 (シリーズ確率と情報の科学)
・統計的因果推論 -モデル・推論・推測-
初めての方なら「岩波データサイエンス Vol.3」から出発して因果推論とは何かを雰囲気を掴んでから「調査観察データの統計科学―因果推論・選択バイアス・データ融合 (シリーズ確率と情報の科学)」に行くと進みやすいのではないかと思います。
「統計的因果推論 -モデル・推論・推測-」はJudea Pearl氏の著書を黒木先生が翻訳したものになります。
バックドア基準や今回は省いたベイジアンネットワークについて詳細に書かれています。
ただ難解であるので最初からここに挑戦するのはオススメしません。
また、統計的因果探索に関しては「統計的因果探索 (機械学習プロフェッショナルシリーズ)」が入門書として読みやすいと思います。
一般的な統計的因果推論についても記載されていますが、あくまで因果探索が主なので傾向スコアなどは出てきません。
・統計的因果探索 (機械学習プロフェッショナルシリーズ)
さらに統計に関してオススメの書籍をこちらにまとめていますので良ければご覧ください！
スタビジのコンテンツをさらに深堀りしたコンテンツが動画と一緒に学べるスクールです。
プレミアムプランでは私がマンツーマンで伴走させていただきます！ご受講お待ちしております！
