不均衡データの対策方法と評価指標！SmoteをPythonで実装して検証していく！

こんにちは！

データサイエンティストのウマたん(@statistics1012)です！

実データを扱っていると度々現れるのが不均衡データ！

不均衡データとはデータの比率に偏りがあるもの。

金融取引の不正利用データやメールのCVデータなど、母数が大量にありその中で該当する正例が非常に少ないケースはよくあります。

そんな不均衡データを通常通り分析してしまうと少々不都合があるんです。

この記事では、そんな不均衡データの扱い方について徹底的に見ていきますよー！

以下の動画でも解説しています！

不均衡データにはどんな問題があるのか

不均衡データとは「データ構造に偏りがあるデータ群」のことを指します。

例えばクレジットカードの不正利用を判別したいとしましょう。

その場合、ほとんどのデータは正常と一部のデータが異常という不均衡データになります。

仮に正常データと異常データの比率が999:1だとしましょう。

このデータを使ってそのまま分類モデルを構築するとどのような問題が生じるのでしょうか？

どういうことか説明していきます。

仮にこのデータに対して、全てのデータを正常と判定する分類モデルを作ったとしましょう。

すると、データの予実は以下のようなマトリックスで表されますね。

本来正常のデータは全て正常と予測され、本来は異常のデータは正常と予測されてしまっています。

この場合、予実の精度は999/1000=99.9%となるのです。

これだけ見るといかにも精度が高そうに見えますが、その裏には不均衡データという罠が潜んでいるのです。

これは極端な例ですが、多くの実データは少なからず不均衡の要素を持っているので分類モデルを作る際には細心の注意が必要になってくるのです。

不均衡データの扱い方と対処法

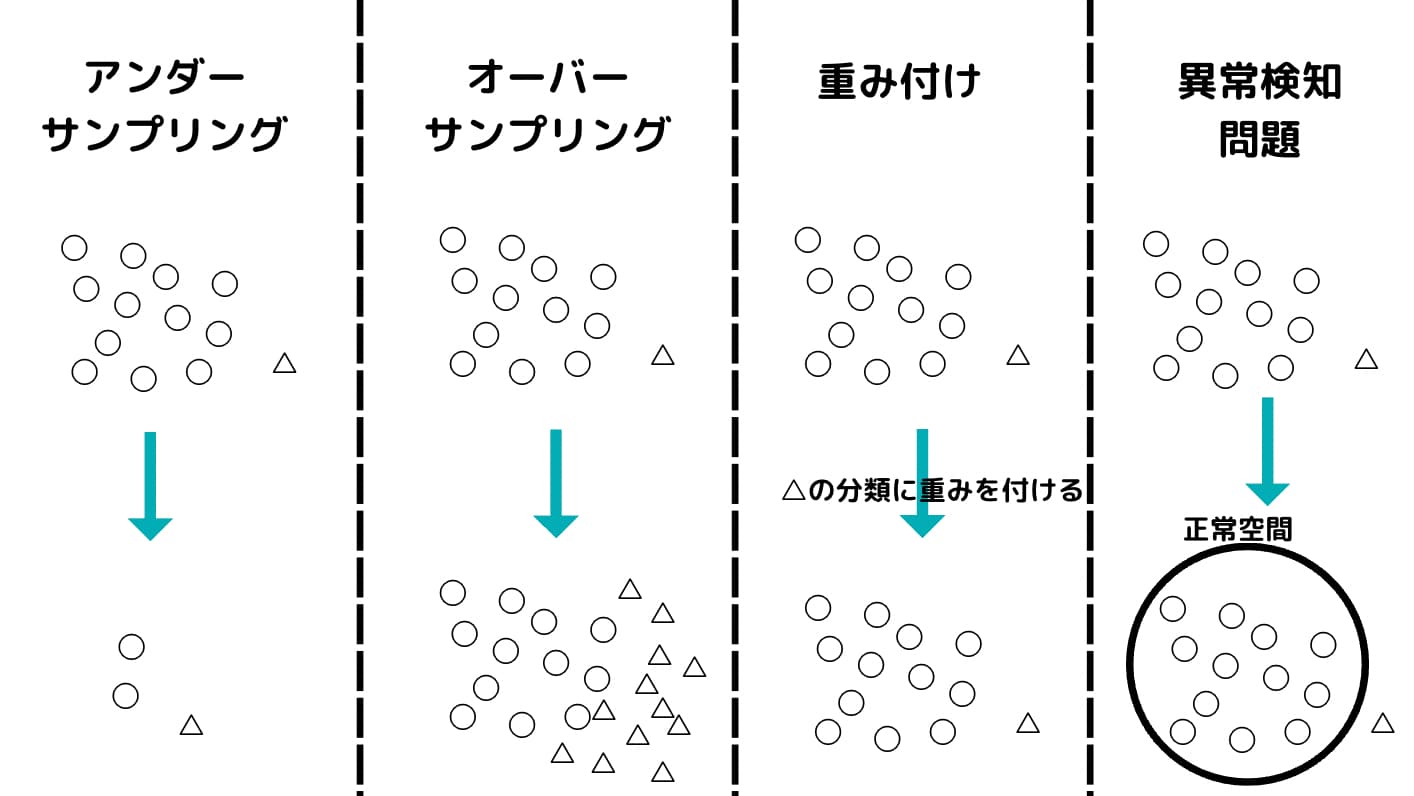
それでは、そんな不均衡データを解消するためのテクニックをいくつか見ていきましょう！

不均衡データの解消には大きく分けて4つの方法があります。

それぞれについて詳しく見ていきましょう！

アンダーサンプリング

最も定番なのがアンダーサンプリング。

シンプルに「少数派のデータ群にあわせて多数派のデータ群を削除する」という方法です。

直感的に分かりやすく、スタンダードな方法になります。

削除する方法はいくつかありますが、以下のような方式が考えられます。

A群とB群を識別する上で重要なのは、A群とB群の境界線付近に分布するデータ。

そのため、境界線付近以外に分布するあまり意味のないデータは削除してA群とB群のデータバランスを取る。

もしくは、全体のデータのバランスを崩さないために多数派群をクラスター分類し各群から均等にランダムサンプリングするという方法。

いくつかの方法がありますが、最もカンタンで分かりやすい方法です。

オーバーサンプリング

続いてオーバーサンプリング。

オーバーサンプリングはアンダーサンプリングとは違い、逆に「少数派のデータを多数派にあわせて増やす」という方法です。

オーバーサンプリングの中で特によく使われる手法がSMOTEと呼ばれるものです。

SMOTEは、Synthetic Minority Over-sampling TEchniqueの略でK近傍法のアルゴリズムを利用して少数派のサンプルを増やしていきます。

K近傍法は以下の記事で詳しくまとめているので参考にしてみて欲しいのですが、

【5分でわかりやすく解説】ｋ近傍法とは？理論とRでの実装方法！当サイト【スタビジ】の本記事では、アルゴリズムがシンプルで分かりやすいk近傍法について理解を深めていきます。最終的にはRでの実装を行うことで理論と実装の両輪を理解していきましょう！

あるサンプルに対して近傍のK個のデータから判別を行うというシンプルなロジック。

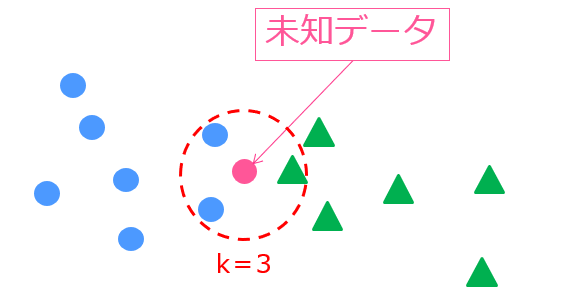
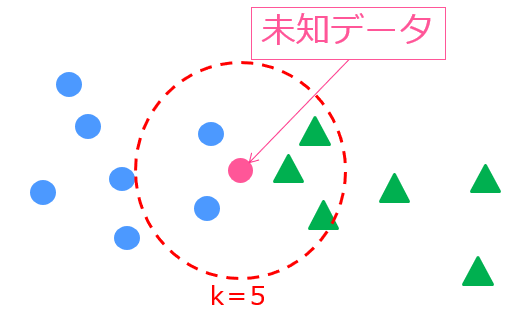
この場合K=3であれば未知データは青〇だと分類され、K=5であれば緑△だと判別されます。

K近傍法の場合は、未知データに対しての判別に使いますがSMOTEではこれをオーバーサンプリングに利用します。

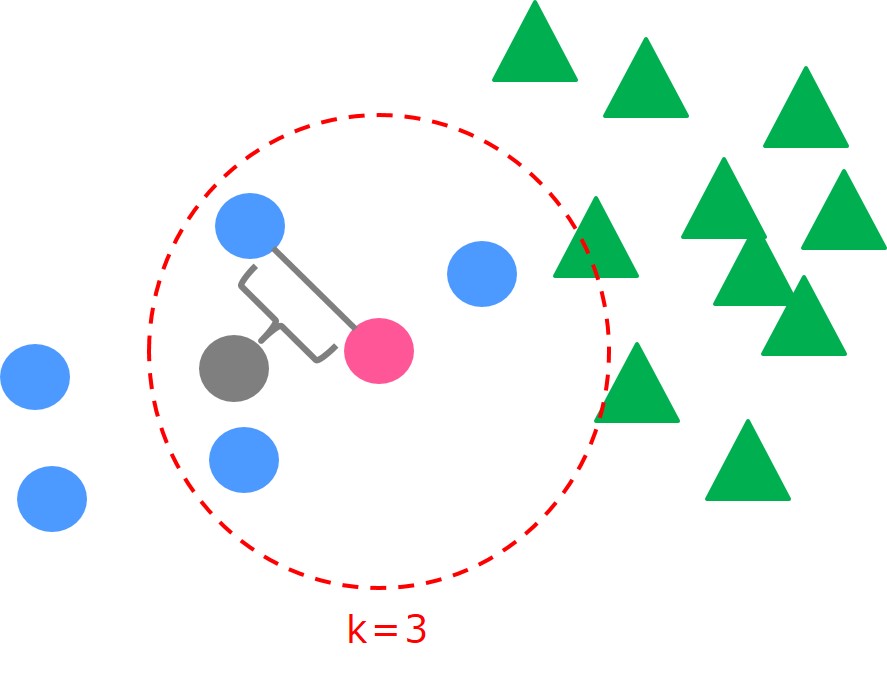
ある少数派のサンプル（ピンク）を選び、k＝３であれば「近傍3つの少数派データからランダムで1つ選び新たなサンプルを内挿する」というロジック。

それを少数派のサンプル全てに適応するというシンプルなアルゴリズムです。

kというパラメータを大きく設定すれば、遠いサンプルとの間に新たなサンプルを内挿することになります。

内挿の仕方は通常のSMOTEではランダムですが、SMOTEの拡張モデルで様々なロジックが開発されています。

重み付け

少数派のサンプルに対して重みを付けて重要視するという方法もあります。

例えば、よく分類問題に使われる勾配ブースティング手法の1つであるXgboostではそれぞれのサンプルごとに重みを付けることができます。

Xgboostは決定木をアンサンブル学習させたものですので、基本的には決定木モデルになります。

決定木モデルではある特徴量において分類した場合の損失関数を基に分類を行いますが、少数派カテゴリはなかなか出てこないので分類できなくても損失にあまり影響を及ぼしません。

そこで少数派の重みを高めて少数派カテゴリも上手く分類できるようにしようというのが、不均衡データに対する重み付けアプローチになります。

異常検知問題として扱う

あまりにもデータに偏りがある場合は、そもそも問題の定義を分類問題ではなく異常検知問題として扱ってしまうという方法もあります。

クレジットカードの不正利用データについては、異常検知問題としてもよさそうですね。

異常検知問題では、正常データを基に正常空間を作り、定めた閾値を超えるデータに関しては異常値とみなします。

品質工学の分野でよく用いられ（不良品の検出など）、以下のような手法があります。

MT法や管理図には様々な派生手法がありますので、ぜひチェックしてみてください。

異常検知問題に関して勉強したい方は以下の記事でおすすめ書籍をまとめているのでチェックしてみてください！

異常検知の様々な手法（古典的・機械学習）を紹介しオートエンコーダをPythonで実装していく！当サイト【スタビジ】の本記事では、異常検知の様々な手法を古典的なものから機械学習領域のものまでいくつか紹介していきます。またその中からオートエンコーダというディープラーニングのアーキテクチャを使った異常検知をPythonで実装していきます！

不均衡データ対処後の評価指標

さて、不均衡データをどのように対応したらよいのかについて見てきましたが分類データを正しく分類できたかどうかはどのように評価したらよいのでしょうか？

ここでは、分類データを正しく評価する指標について見ていきたいと思います。

正解率(Accuracy)

さきほどのクレジットカードの不正利用の例をそれぞれマトリックスに当てて見てみましょう！

まず最も分かりやすいのが正解率（Accuracy）！

これは、

$$Accuracy=\frac{a+d}{a+b+c+d}$$

で表します。

シンプルに全てのサンプルの中で実測値と予測値が一致した割合ですね。

少し数値をいじり以下のようになったとしましょう！

このような例だと正解率は900/1000=90％となります。

適合率(precision)

他にもいくつか指標があります。

適合率（precision）は以下のように求めます。

$$Precision=\frac{a}{a+c}$$

異常と予測されたクラスのうち実際に異常だったクラスの割合が適合率になります。

この場合は100/180=約56％になります。

再現率(recall)

続いて、再現率（recall）！

再現率は以下のように求めます。

$$recall=\frac{a}{a+b}$$

実際に異常だったクラスのうち、どのくらい異常と予測されたかです。

こちらは、100/120=83%となりました。

実は適合率と再現率はトレードオフの関係になります。

F-measure

そしてそれら適合率と再現率を組みあわせて作られた指標がF-measureというものです。

F-measureは適合率と再現率の調和平均を取ります。

$$F-measure=\frac{2}{\frac{1}{適合率}+\frac{1}{再現率}}$$

機械学習における評価フェーズに関しては以下の記事で詳しく解説しております！

機械学習の分類・予測精度における評価指標を徹底解説！当サイト【スタビジ】の本記事では、機械学習を実装する上での評価指標について徹底的にまとめていきます！回帰タスクや分類タスクにおける評価指標について見ていきましょう。評価フェーズや評価における注意点についても解説していきます。

不均衡データを実際にPythonで分析（SMOTE）

それでは、そんな不均衡データを実際にPythonで分析していきます。

今回取り扱うのは、何度も登場しているクレジットカードの不正使用データ。

データ解析コンペKaggleで公開されているデータを使っていきます。

以下のURLからダウンロードしましょう！

import pandas as pd
data = pd.read_csv("creditcard.csv")

まずは、クレジットカードデータを読み込んでいきます。

ここでクレジットカードの構造を確認しておきましょう！

print(data.shape)
print(data["Class"].value_counts())

(284807, 31)
0    284315
1       492

31項目があり、284807のサンプルがあるようです。

さらに不正利用のクラスはそのうち492とあきらかな不均衡データになっています。

そんな不均衡データをまずは、そのまま分析してみましょう！

y_data = data["Class"]
x_data = data.drop("Class",axis=1)

from sklearn.model_selection import train_test_split as tts
x_train,x_test,y_train,y_test = tts(x_data,y_data,test_size=0.1)

データを説明変数と目的変数に分け、さらにテストデータと学習データに分けます。

from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
lr.fit(x_train, y_train)
y_pred = lr.predict(x_test)

from sklearn.metrics import confusion_matrix, accuracy_score, precision_score, recall_score, f1_score

print('confusion matrix = \n', confusion_matrix(y_true=y_test, y_pred=y_pred))
print('accuracy = ', accuracy_score(y_true=y_test, y_pred=y_pred))
print('precision = ', precision_score(y_true=y_test, y_pred=y_pred))
print('recall = ', recall_score(y_true=y_test, y_pred=y_pred))
print('f1 score = ', f1_score(y_true=y_test, y_pred=y_pred))

そして、今回は単純にロジスティック回帰を使って分類をしていきます。

最後に混合マトリクスと正解率、適合率、再現率、F-measureを指標として算出しています。

confusion matrix = 
 [[28420    11]
 [   19    31]]
accuracy =  0.9989466661985184
precision =  0.7380952380952381
recall =  0.62
f1 score =  0.6739130434782609

正解率は99.9％と非常に高いですが、再現率は62％になっていて実際に不正をした人のうち62％しか見抜けていないということになります。

不正を見抜くモデルとしてこれは果たして妥当なのでしょうか？

それでは、ここでSMOTEを使ってオーバーサンプリングしていきましょう！

!pip install imblearn

imblearnというライブラリをインストールします。

from imblearn.over_sampling import SMOTE
sm = SMOTE()
x_resampled, y_resampled = sm.fit_sample(x_train, y_train)

そしてSMOTEをインポートして・・・こんなにカンタンに使えちゃうんです。

さて、実際に少数派データを増やすことができたか確認してみましょう！

y_resampled.value_counts()

1    255884
0    255884

少数派データが多数派データを同じサンプル数になっているのが分かります。

それでは、ここから同様にロジスティック回帰をおこなっていきましょう！

lr = LogisticRegression()
lr.fit(x_resampled, y_resampled)
y_re_pred = lr.predict(x_test)


print('confusion matrix = \n', confusion_matrix(y_true=y_test, y_pred=y_re_pred))
print('accuracy = ', accuracy_score(y_true=y_test, y_pred=y_re_pred))
print('precision = ', precision_score(y_true=y_test, y_pred=y_re_pred))
print('recall = ', recall_score(y_true=y_test, y_pred=y_re_pred))
print('f1 score = ', f1_score(y_true=y_test, y_pred=y_re_pred))

結果は・・・

再現率は62％から84％になりました。

これで不正利用データの84％を見抜くことができます。

ただ、それに伴って適合率が大きく下がり8％になってしまっています。

すなわち不正だと判定した人のうち92％は正常であるということですね。

この適合率と再現率は、統計の第1種の過誤・第2種の過誤と同じ考え方でありモデル構築者に毎回付きまとう問題です。

今回のケースは不正利用データがあまりにも少なく2値分類であるため異常値問題として分析してもよかったかもしれません。

不均衡データの扱い方　まとめ

本記事では、不均衡データについて様々な観点からみてきました。

不均衡データは実データで非常に多く存在するクセのあるデータセットです。

分析する前にデータセットの傾向を確認し不均衡ではないか必ず確認するようにしましょう！

最後に不均衡データの解決方法と評価指標についてまとめておきます。

不均衡データの対処方法はデータサイエンスにおける1つの方法論。

データサイエンティストへのロードマップや機械学習・Pythonの勉強法を以下の記事でまとめているのでぜひチェックしてみてください！

【5分で分かる】データサイエンティストに必要なスキルと独学勉強ロードマップ！当サイト【スタビジ】の本記事では、データサイエンティストに求められるスキルとそれを身に付けるための勉強法について徹底的にまとめていきます！入門者でも、しっかりデータサイエンティストについて理解しある程度独学で駆け出しの状態までいけることを目指します。 【5分で分かる】機械学習の独学勉強ロードマップを徹底的にまとめていく！当サイト【スタビジ】の本記事では、機械学習の独学勉強ロードマップについて徹底的にまとめていきます。機械学習をいきなり理論からしっかり勉強しようとすると挫折しかねません。そこで、この記事ではなるべく挫折しないロードマップをお伝えしてきますよ！ 【Python独学勉強法】Python入門を３ヶ月で習得できる学習ロードマップ当サイト【スタビジ】の本記事では、過去僕自身がPythonを独学を駆使しながら習得した経験をもとにPythonを効率よく勉強する方法を具体的なコード付き実装例と合わせてまとめていきます。Pythonはできることが幅広いので自分のやりたいことを明確にして勉強法を選ぶことが大事です。

ちなみにもし、これらを全て包括的に学びたいのであれば当メディアが運営するスクールであるスタビジアカデミー、略して「スタアカ」がオススメです！