管理図とは

こんにちは!
今回は管理図についてまとめていきます。
管理図とは、主に品質の分野で用いられる工程を管理する異常検知手法です。
単一の変数から異常を判断する単変量管理図と複数の変数から異常を判断する多変量管理図の2つに分けて説明していきますよー!
実は、大学院時代に多変量管理図について研究論文をケンブリッジ大学で発表した実績があるくらい多変量管理図に関しては詳しいです。
全世界で当時一番精度の高い手法を考案しました笑
単変量管理図
まずは、単一の変数で工程の異常判定を行う、単変量管理図についてみていきましょう!
・シューハート管理図
最も一般的な管理図です。多くの現場で使われています。
正常工程のサンプルから平均値や中央値、範囲を計算し、それらを元に上方管理限界線と下方管理限界線を求めます。
検査したい工程におけるサンプルの挙動を観察し、管理限界線を越えたら異常とします。
またそれ以外にもサンプルが連続して上方・下方のどちらか片方に7回連続した場合なども異常とみなします。
また、サブグループ(同じ期にいくつかのサンプルがある状況)における管理図としてX¯−R管理図やX¯−s管理図などがあります。
群の中での特性値、平均X¯と範囲Rを計算し、それらの特性値ごとに管理図を描いて管理するというものです。X¯管理図とR管理図の二つで管理します。
先ほどのシューハート管理図におけるσは決められた係数によって計算します。(省略)
X¯−s管理図は、この範囲Rが標準偏差sになったもの!何も難しくありませんね!
管理図を使いこなして、工程の異常を検知しましょう

・CUSUM管理図
シュハート管理図は大きな変化は素早く検知することができるが、微小な工程の変化には対応していないません。
そこで考案されたのが前期と今期の差を足しあわせていくCUSUM(累積和)管理図です!
工程の小さい変化も積み重ねることでいずれ異常として検知できるという考え方なんです。非常に単純な考え方ですが画期的ですねー!

・EWMA管理図
CUSUM管理図と同様に工程の微小な変化に対応している管理図です。
EWMA(指数重みづけ平均変化)管理図と呼びます。
ただ、こちらは過去と現在の値に指数パラメータによって重み付けして統計量を算出しているのでCUSUMとは算出方法が違い精度も違います。
CUSUMのほうが良いとしている文献もあればEWMAのほうが良いとしている文献もありますが、個人的にはEWMA管理図のほうが良いと思います。
現にEWMA管理図のほうが研究が盛んです。
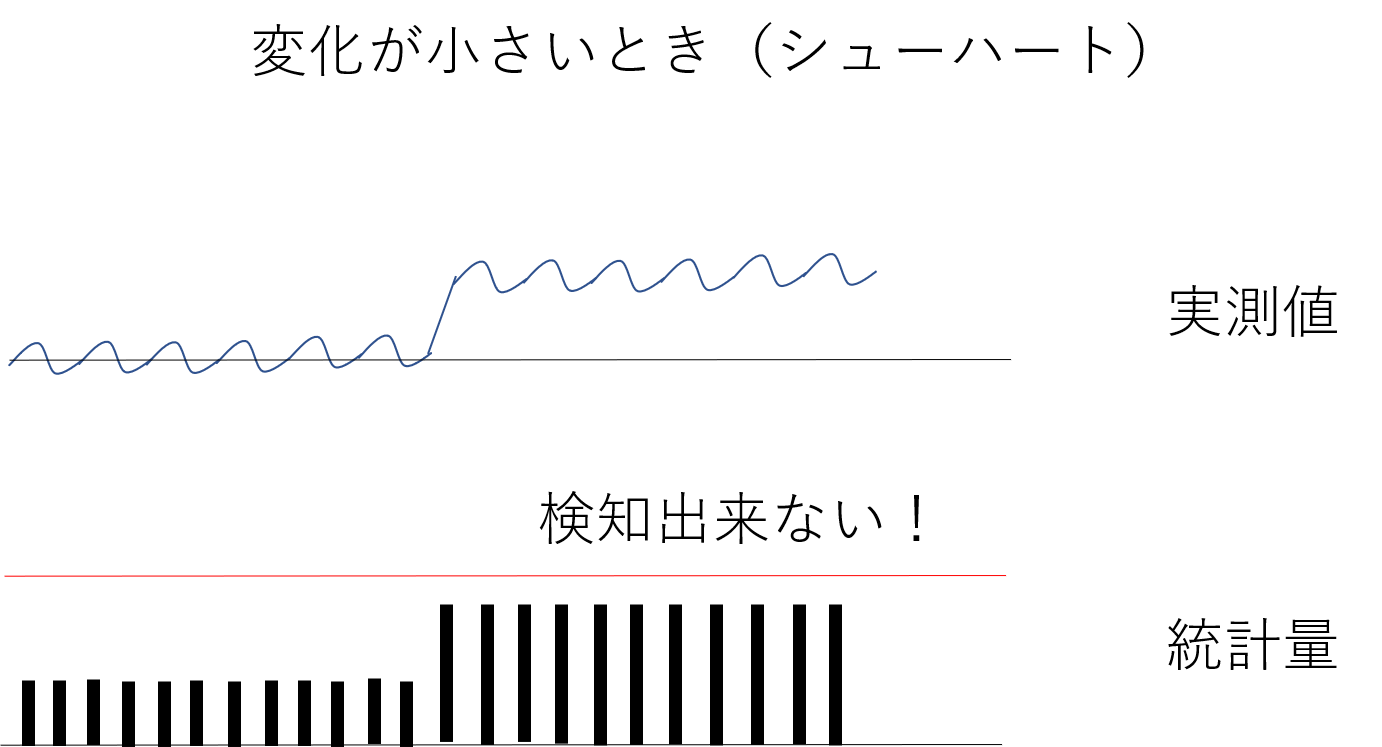
シューハート管理図で検知できないような小さな変化もEWMA管理図を使えば・・・
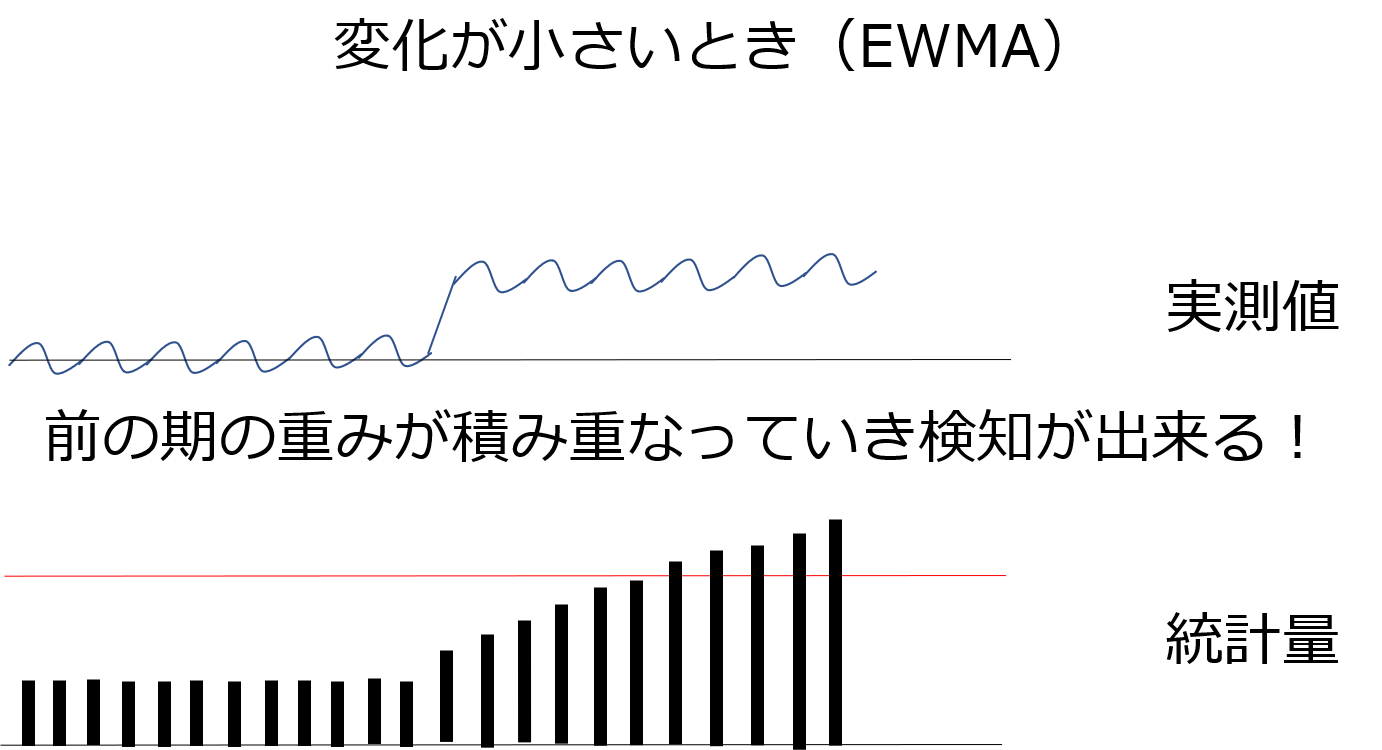
微小な変化が蓄積していき変化を検知できるようになるんです!

多変量管理図
続いて、複数の変数の変化を同時に見て工程の異常判定を行う多変量管理図を見ていきましょう!
複数の変数それぞれに単変量管理図を当てはめて異常を判定することもできますが、多重比較の問題などで不整合です。
そのため多変量管理図によって変数の相関を考慮し異常判定することを推奨します。
単変量管理図では、あらかじめ管理限界線を理論的に算出しますが、多変量管理図では理論的に管理限界線を定めることが難しい場合が多いのでARL(Average Run Length)という評価指標を用いて判定を行います。
評価指標ARL
これは管理限界線を越えるまでどのくらいのサンプルが続いたかを示す指標となります。
単変量では標本平均と標本分散などから理論的に閾値を決められたのですが、MEWMAでは理論的に決めることができません。モンテカルロシミュレーションで求めます。
正常状態のARLをIC-ARL(In control ARL)と呼びこれは大きければ大きいほど良いです。異常状態のARLをOC-ARL(Out of control ARL)と呼びこれは小さければ小さいほど良いです。
基本的にはIC-ARLをいくつかに固定したうえで、OC-ARLの小ささを評価します。
IC-ARLは200,370などが多いようですが、私は専ら200でやっています。
・ホテリングT2管理図
1947年にホテリングという偉人が考案した多変数の工程管理に用いる手法です。
各変数の相関を考慮したマハラノビス距離を用いて異常検知を行います。
非常に汎用性の高い方法で様々な方面で応用されています。

・MCUSUM管理図
CUSUM管理図の多変量拡張版。
更新アルゴリズムはCUSUM管理図とほとんど一緒でそれに従って得られた更新値とマハラノビス距離を用いて最終的な統計量を算出します。
・MEWMA管理図
EWMA管理図の多変量拡張版。
EWMA管理図の要領で更新値を得つつ最終的にマハラノビス距離を用いて統計量を算出します。
この時、最終統計量の算出に用いる分散共分散行列は正常状態の分散共分散行列に指数パラメータを用いて重みづけしたものです。
こちらも同様にホテリング管理図で検知できないような微小な変化も
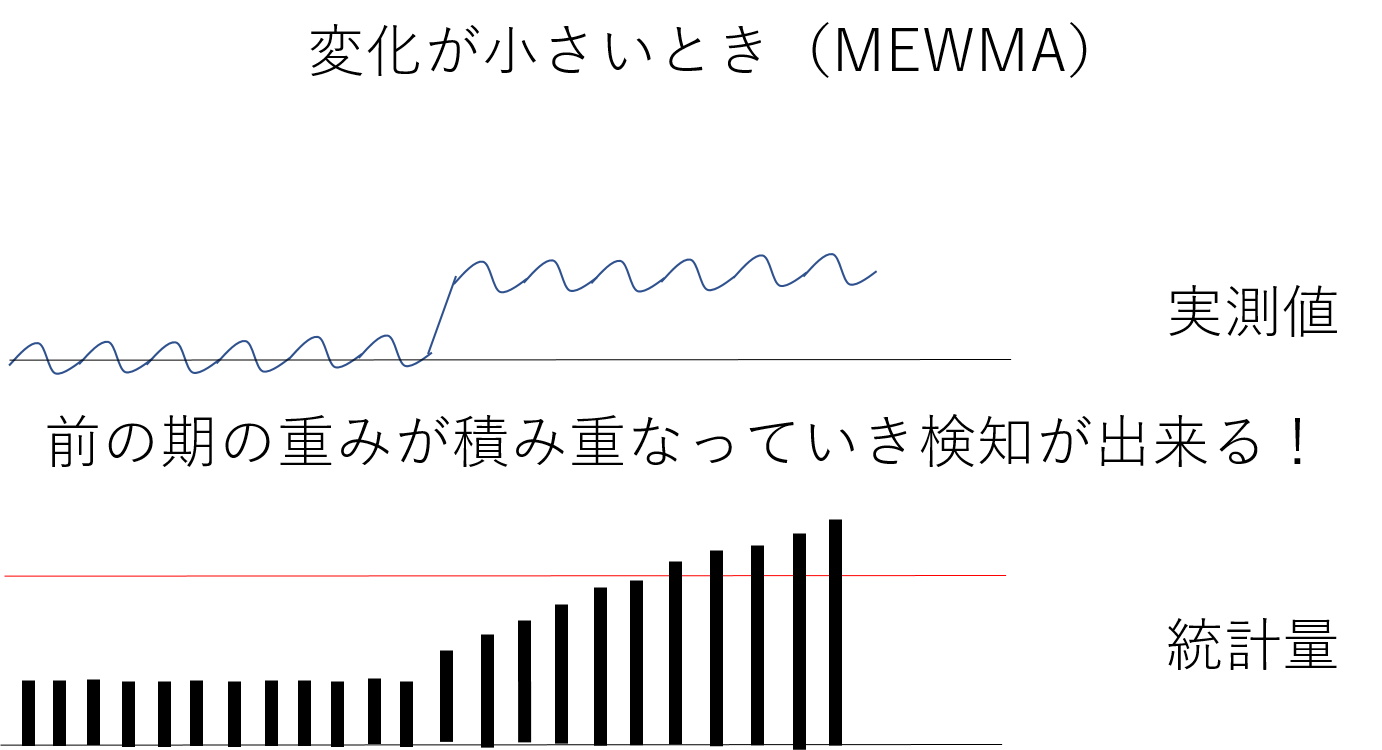
MEWMA管理図では更新されていき検知できるようになるんです!

・MEWMC管理図
ホテリング管理図に対して、微小な変化を検知できるMEWMA管理図!
実務ベースでの実用が期待されます。
しかし、MEWMA管理図が検知できるのは平均ベクトルの変化のみ。
分散共分散行列の変化など多彩な変化を検知することはできません。
そこで登場したのが
MEWMC管理図!
MEWMC管理図は(Multivariate Exponentially Weighted Moving Covariance matrix)の略で、分散共分散行列の変化を可能にした手法です!
ミネソタ大学のMaboudou-Tchao氏が2008年に提案した比較的新しい手法です!
非常に有用な手法で、新しいブレークスルーを起こしました。
MEWMA管理図では検知できないような分散の変化も
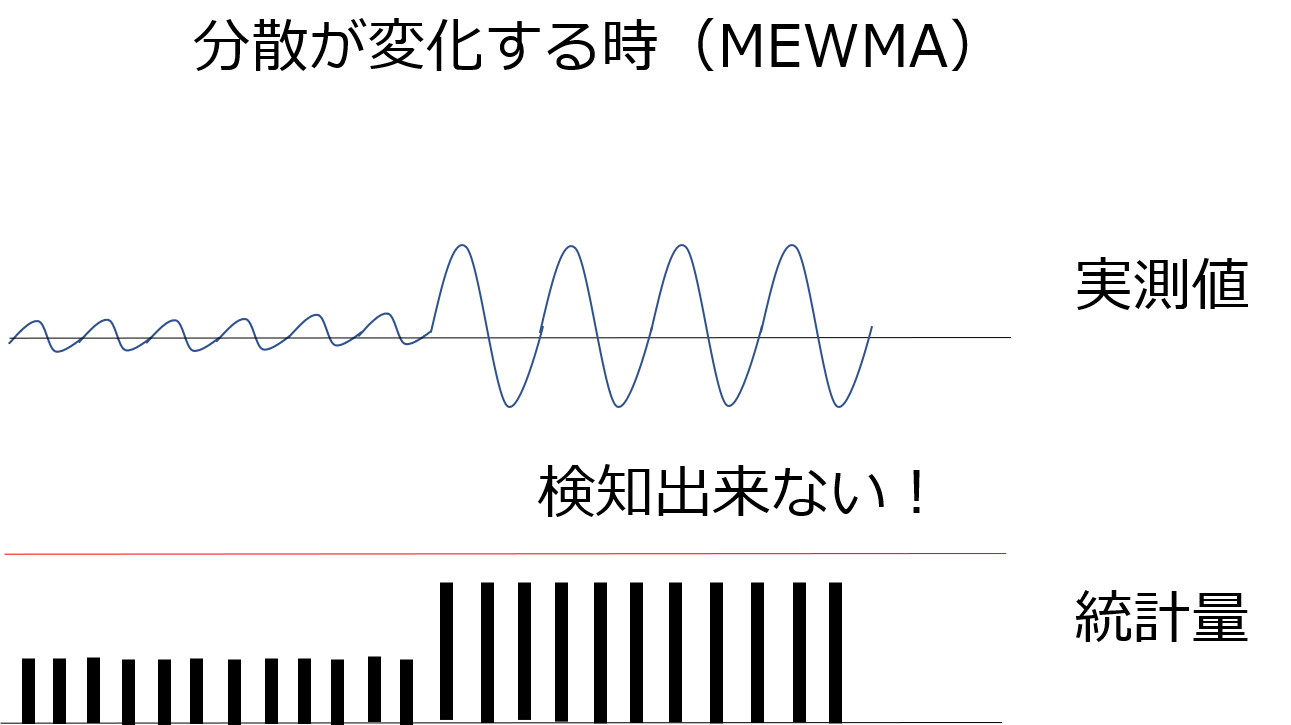
MEWMC管理図を用いれば・・・
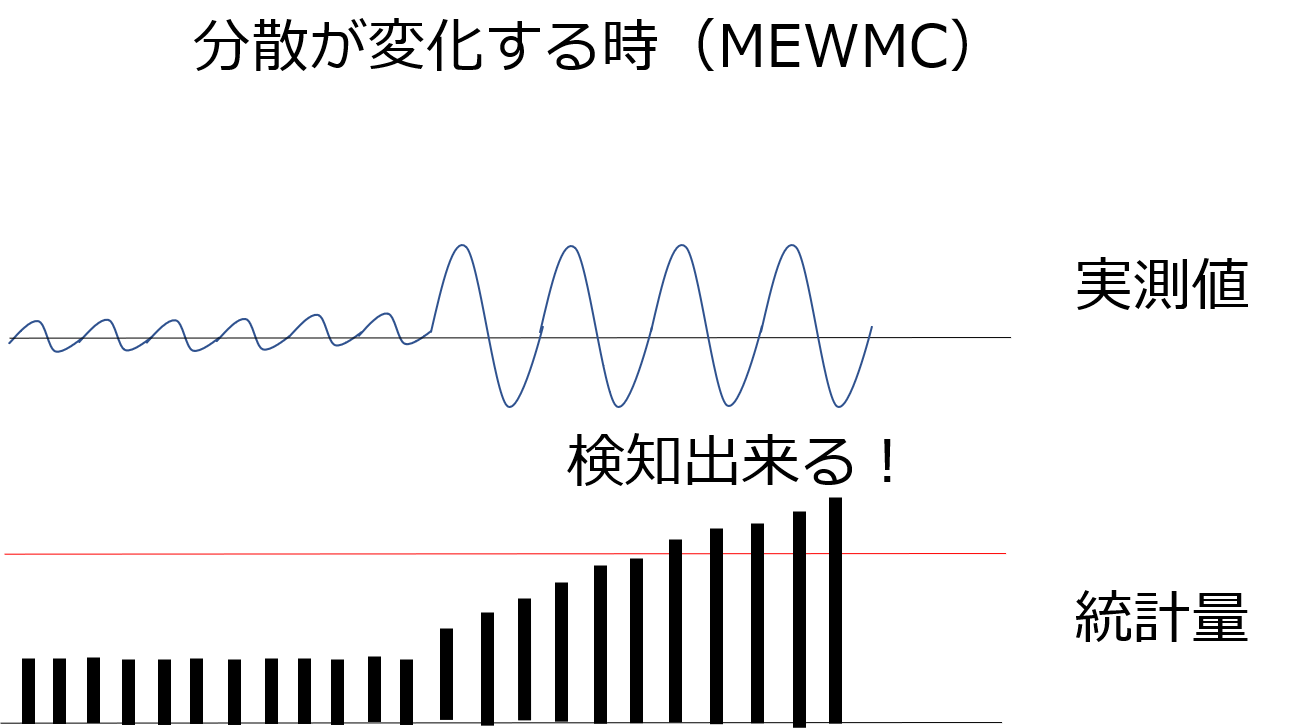
検知できるようになるんです!

・ELR管理図
MEWMA管理図は平均ベクトルの変化
MEWMC管理図は分散共分散行列の変化
を検知します。
しかし、これらの手法は特定の変化が起きる状況でしか検知できません。
変化のパターンが分かっている時には有用ですが、変化のパターンが分かっていない時はどうでしょう。
平均ベクトルが変化しているのにMEWMC管理図を使っていては意味がないし、分散共分散行列が変化しているのにMEWMA管理図が変化していては元も子もありません!
それでは、平均ベクトルと分散共分散行列の変化を同時に検知できる手法はないのでしょうか?
あるんです!それが、
ELR管理図です!
ELR管理図とは、Exponentially Likelihood Ratioの略で、2010年にZhangらが提案した手法です。
平均ベクトルと分散共分散行列の変化に重み付けをした統計量を最終的に対数尤度に代入し変化を検知します。
基本的にはMEWMA管理図やMEWMC管理図と同様のアルゴリズムで重み付けを行い各期ごとに蓄積していきます。
平均ベクトルが変化しても分散共分散行列が変化しても対応できるということで画期的な手法ですね!























