実験計画法についてわかりやすく解説!Pythonで実際に実装!

こんにちは!スタビジ編集部です!
統計学の応用分野である実験計画法(Design Of Experiments)。
近年発展している機械学習手法などと比較するとかなり単純な理論構成ですが、今もなお品質管理などの分野において頻繁に用いられている手法です。
この記事では、そんな実験計画法の特徴とPythonでの実装を見ていきたいと思います。
以下の動画でも詳しく解説しているのであわせてチェックしてみてください!
目次
実験計画法とは

実験計画法とは、効率のよい実験計画を設計し、結果を適切に解析することを目的とした方法論です。
フィッシャーが20世紀初頭に創始しました。
実験計画法には様々な手法がありますが、それらを使っていく上で共通に理解しておくべき2つのポイントがあります。
1. 平方和の分解
2. 交互作用
少しわかりづらいので図で表すとこんな感じ。
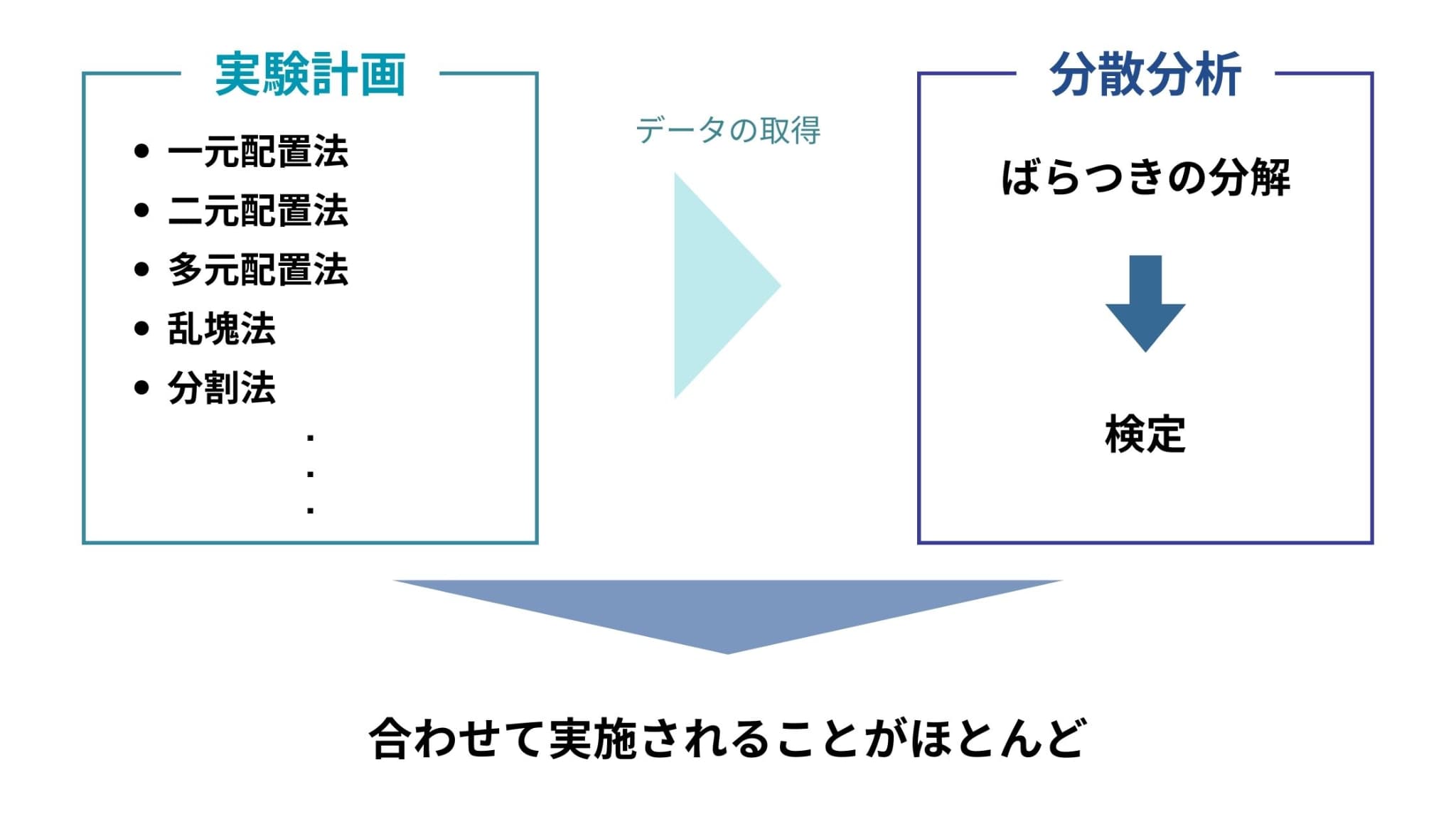
つまり、実験計画法という方法論を用いて効率のよい実験を計画し、分散分析を用いて統計的に解析を行うということです(いきなり調査データに対して分散分析を行うこともあります)。
ただし実験計画から解析までをセットで行うことが多いので、入門書などでは分散分析を行うプロセスまで含めて実験計画法として紹介されていることがほとんどです。
ゆえに、平方和の分解と交互作用はしっかりと押さえておきましょう。


実験計画の3原則

実験計画法では統計的判断を活用しています。
そしてその基準はデータから推定される誤差です。
ゆえに、誤差を精度よく求めることが誤った判断をしないために重要であると言えます。
そこで実験計画法の創始者であるフィッシャーは、実験の場を以下の3つの原則に従って管理することを提唱しました。
1. 反復(replication)
2. 無作為化(randomization)
3. 局所管理(local control)
これらは実験計画の3原則と呼ばれています。
1. 反復(replication)
誤差を評価するためには、同一の条件下で実験を繰り返すことが必要です。
また、繰り返しのデータの平均をとることにより、母平均やその差の推定誤差も向上していきます。
2. 無作為化(randomization)
実験で発生する誤差は偶然誤差だけではありません。
例えば、室温を特に制御せずに実験を行うとき、朝から昼にかけて室温は徐々に上昇し、夜に向けては徐々に下降していきます。
このような誤差を系統誤差と呼びます。
系統誤差の管理や評価が難しい場合、実験条件を時間的、空間的に無作為(ランダム)にわりつけることによって、系統誤差を偶然誤差に転化することが可能になります。
3. 局所管理(local control)
局所管理の原則とは、実験の場を適当なブロックに分け、ブロック内では条件をなるべく均一になるようにし、効果の検出力と比較の精度の向上を図ることです。
これは、系統誤差を回避するためのもう1つの方法です。
系統誤差を発生させるおそれのある時間的、空間的要因をブロックに分け、そのなかに比較したい全ての処理を入れることで、系統誤差の大きい部分はブロック間の差異として取り出し、その分誤差のばらつきを減らすことができます。
実験計画法の種類

実験計画法には、以下のような手法があります。
1. 一元配置法
2. 二元配置法
3. 多元配置法
4. 直交表を用いた実験計画
5. 乱塊法
6. 分割法
7. 枝分かれ実験
様々な実験の条件や目的に合った手法を選択し、解析まで行なっていきます。
適用例(直交表を用いた実験計画)

ここから、直交表を用いた実験計画の適用例を説明していきます。
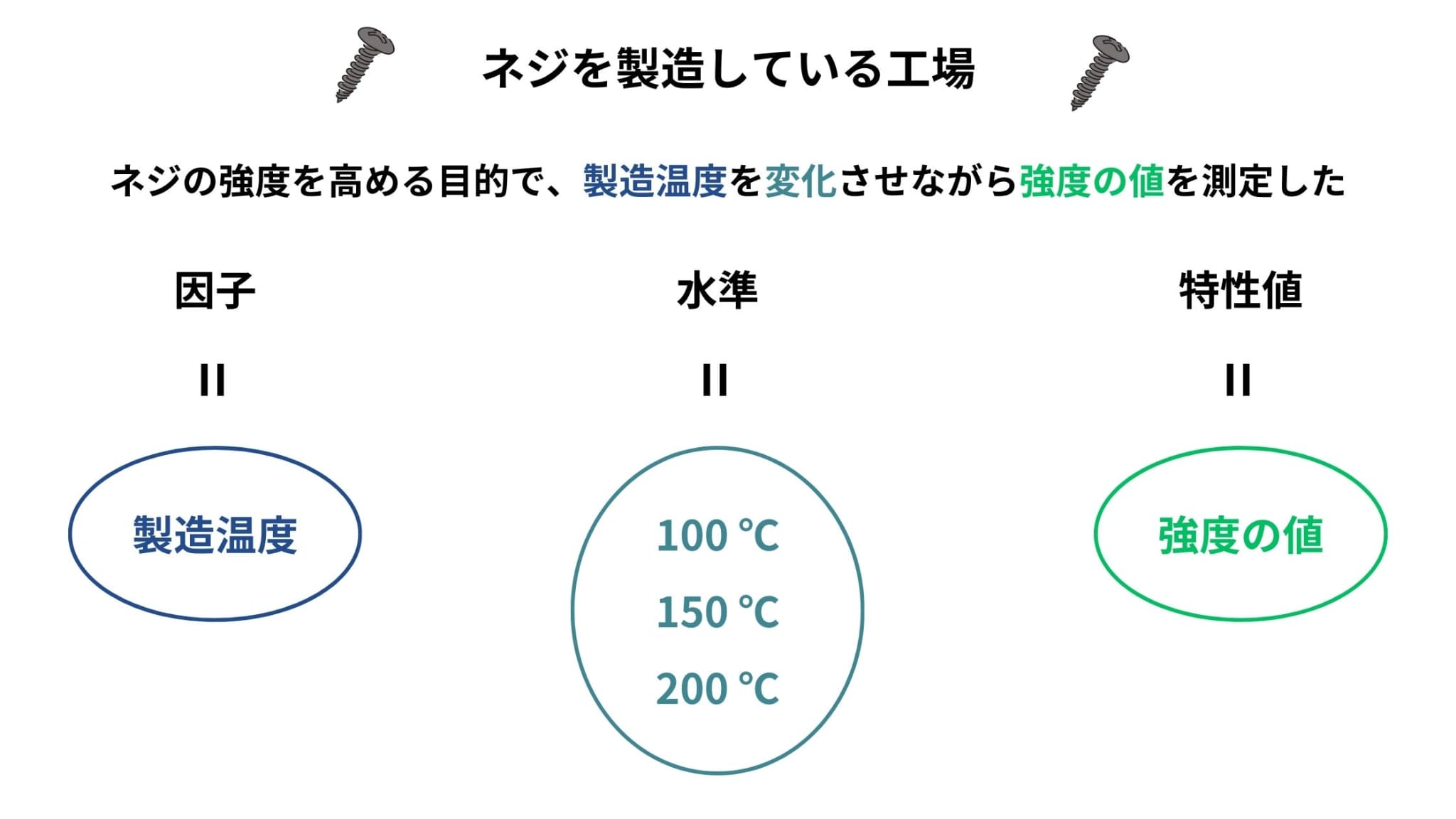
1. 語句の説明
分散分析の記事でも語句の説明はされていますが、改めてここで説明しておきます。
因子は、ばらつきの要因のことを指します。
水準は、因子を量的、あるいは質的に変えた具体的な条件です。
また、実験の結果得られるデータのことを特性値と呼びます。
以下の図は、それぞれの語句の例を示したものです。
2. 直交表とは
一元配置法や二元配置法、多元配置法は、まとめて要因配置実験と呼ばれます。
要因配置実験は、簡単に言うと全ての水準組み合わせで実験を行う方法です。
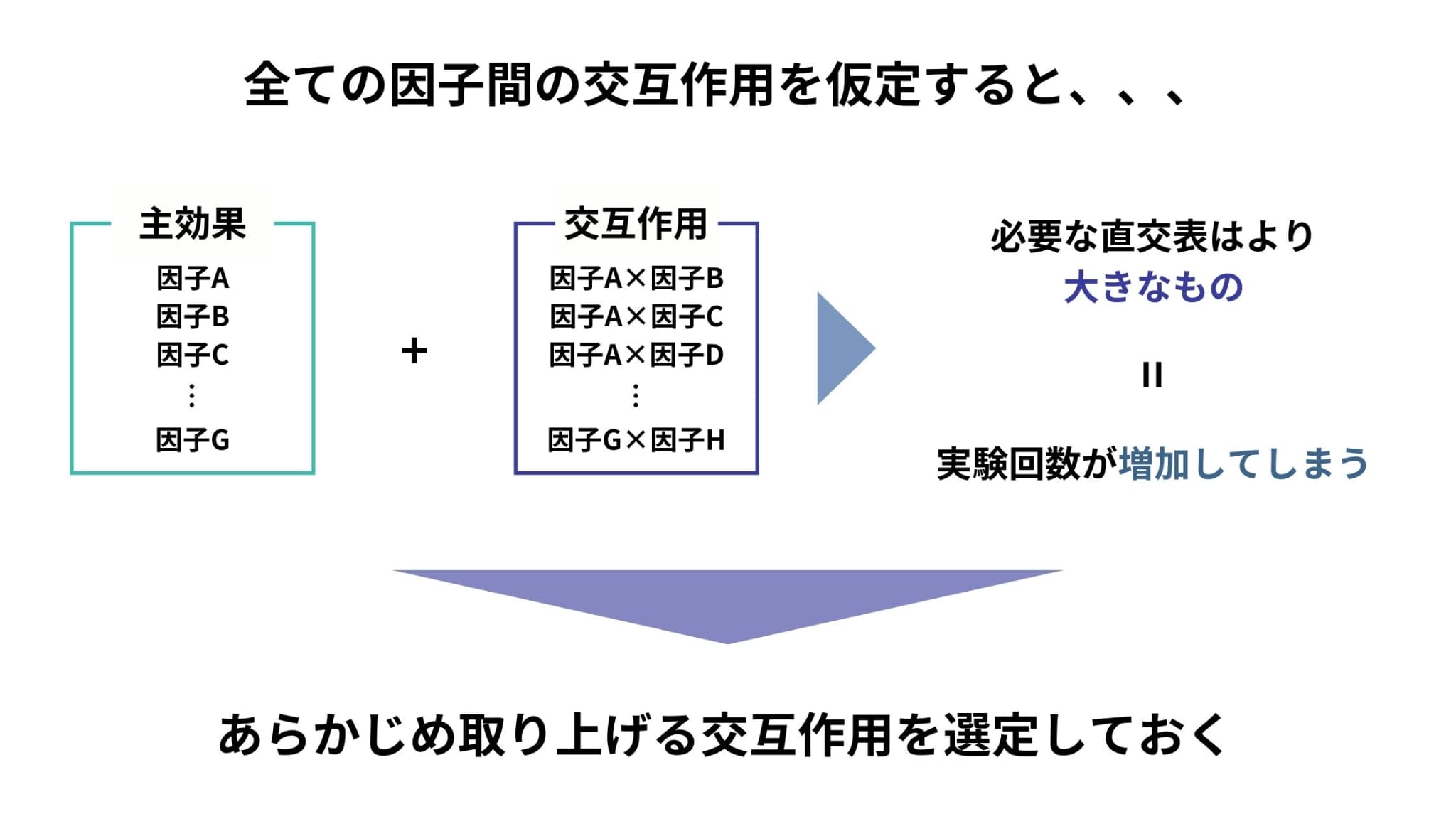
しかし、たくさんの因子を取り上げた要因配置実験では、実験回数がかなり多くなってしまうというデメリットがあります。
例えば7つの因子(各2水準)を取り上げた場合、全ての因子間に交互作用が存在すると仮定すると、27=128回の実験が必要になり、かなり非効率です。
そこで、実験回数を減らしてくれる直交表の出番というわけです。
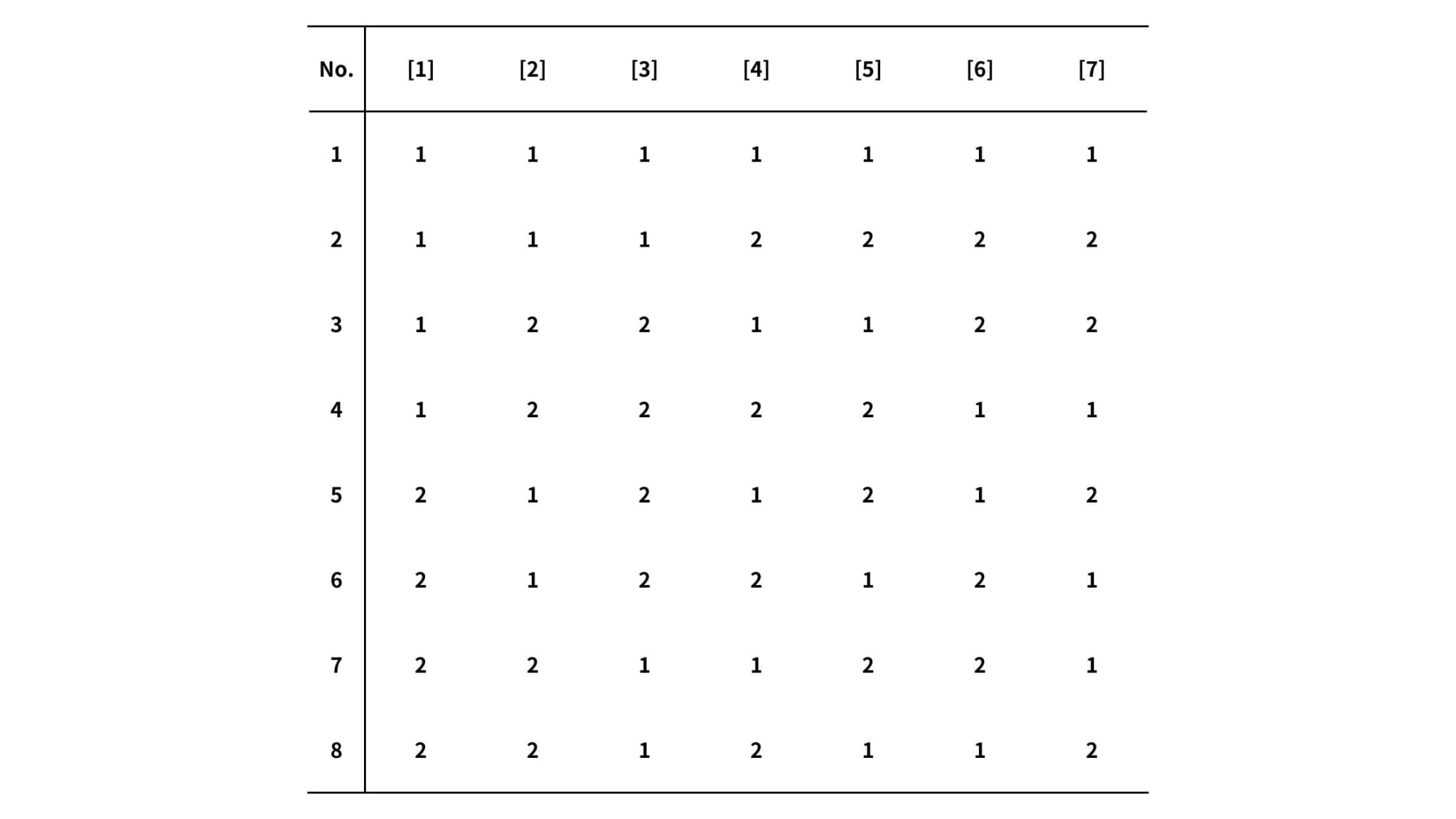
上の表は、2水準系直交表の1つであるL8直交表です(3水準系直交表などもあります)。
L8直交表には、2水準の因子を最大7つまで(=列の数)適用することができます。
表内の数字は各因子の水準を表しており、任意の2因子間の水準の組み合わせが均等になるように配置されています。
つまり、L8直交表を用いる場合、たった8回(=行の数)の実験で最適な水準組み合わせを見つけることができるのです。
ただし、直交表を用いる際、以下のことに注意してください。
2因子間の交互作用を「検討すべきもの」と「無視できるもの」にあらかじめ区分する必要がある
先ほど「全ての因子間に交互作用が存在すると仮定した場合」と述べましたが、現実的には3因子以上の交互作用は存在しないことが多く、直交表を用いた実験においては無視する(誤差としてまとめる)ことがほとんどです。
そのため、考慮すべきなのは2因子間の交互作用になるわけですが、それが全ての因子間で存在すると仮定してしまうと結局実験回数が増えてしまいます。
ゆえに、技術的側面などを考慮して、あらかじめ取り上げる交互作用とそうでないものを区分しておくことで、より少ない回数の実験で解析を進めていくことができます。
3. 適用例
ある工場では、コンクリート製のタイルを製造しています。
しかし、タイルの強度にはばらつきがあることが判明しました。
そこで、タイルの強度を最も高める製造条件を探すため、実験計画法(実験計画&分散分析)を適用します。
因子と水準の決定
今回の例では、以下の因子と水準を取り上げます。
・成型圧力(A):A1 A2
・成型時間(B):B1 B2
・乾燥温度(C):C1 C2
・乾燥時間(D):D1 D2
・熱処理温度(F):F1 F2
・熱処理時間(G):G1 G2
・冷却温度(H):H1 H2
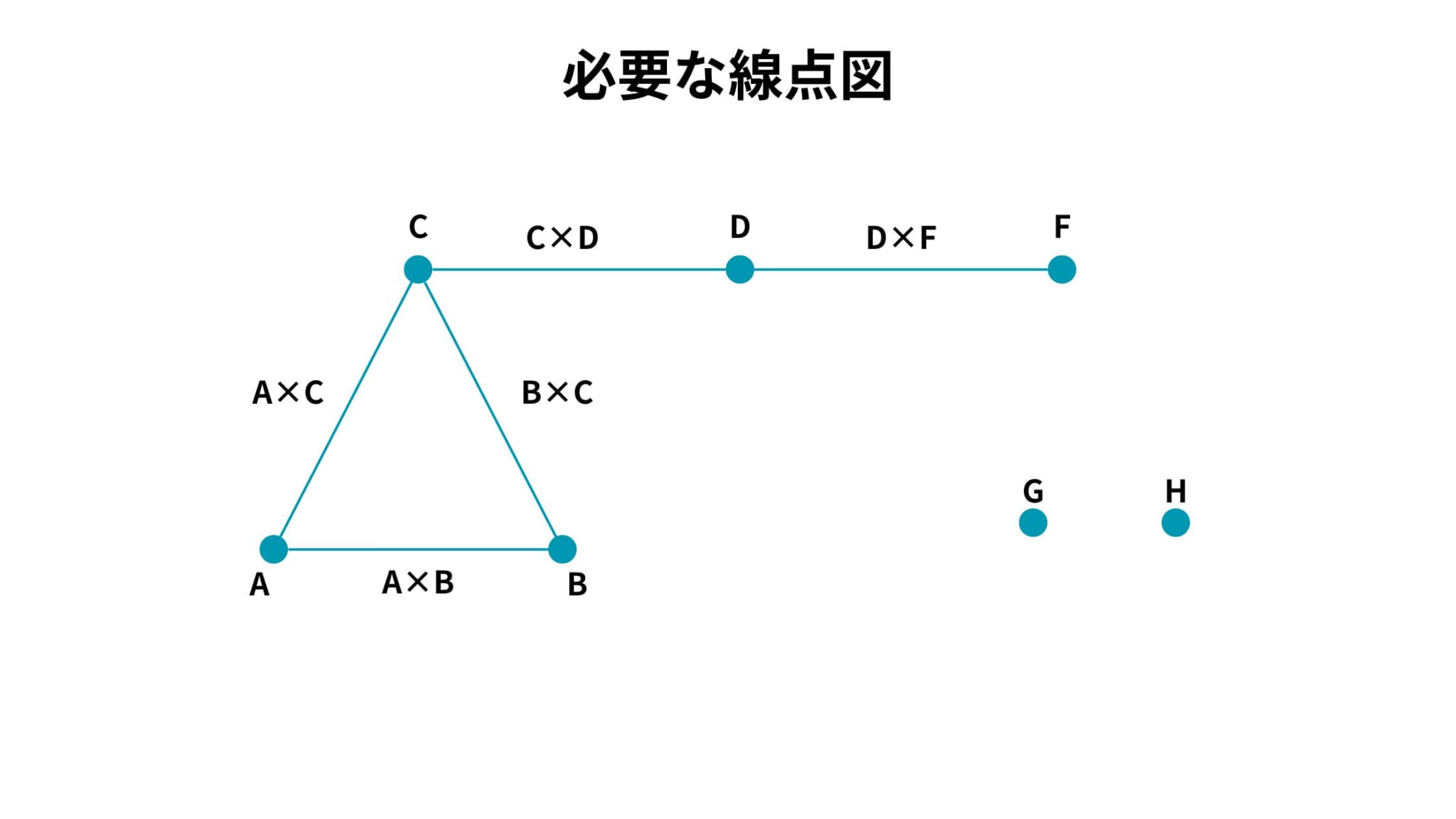
また、技術的側面を考慮し、A×B、A×C、B×C、C×D、D×Fの5つの交互作用を取り上げることにしました。
さらに、特性値はタイルの強度で、大きいほどよいとします。
因子の割り付け
続いて取り上げた因子と交互作用を直交表に割り付けていきます。
因子数は7、交互作用は5の合わせて12であるので、L16直交表を用いることにします。

ただし、ここに適当に因子や交互作用を割り付けてはいけません。
線点図を用いて割り付けを決定していきます。
線点図とは、因子を点で表し、2点を結んだ線分を交互作用に対応させたグラフです。
また、実験者が取り上げた因子と考慮する交互作用を表現したものを必要な線点図、それぞれの直交表に応じて用意されているものを用意されている線点図と呼びます。
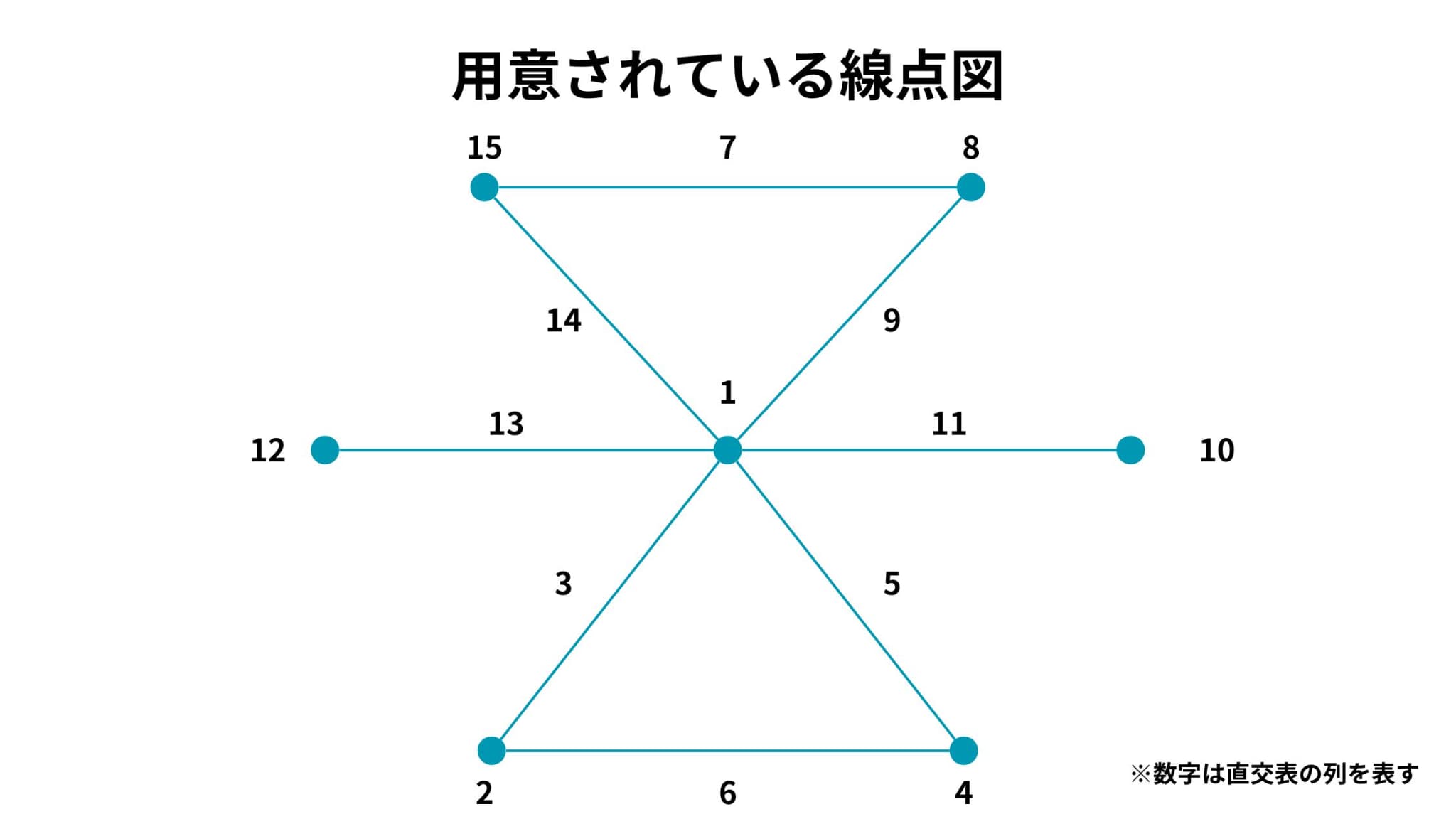
今回の事例における、必要な線点図と用意されている線点図は以下のようになります。
また、L16直交表について用意されている線点図は他にもいくつか存在します。
線点図を用いて割り付けることで、因子の主効果と交互作用が混ざってしまうことを防ぐことができます。
例えば、用意されている線点図の一番下は、2と4が線分6によって結ばれています。
これは、直交表の第2列と第4列に割り付けた因子の交互作用が第6列に現れることを示しています。
必要な線点図を用意されている線点図に組み込むと、以下のような線点図になります。
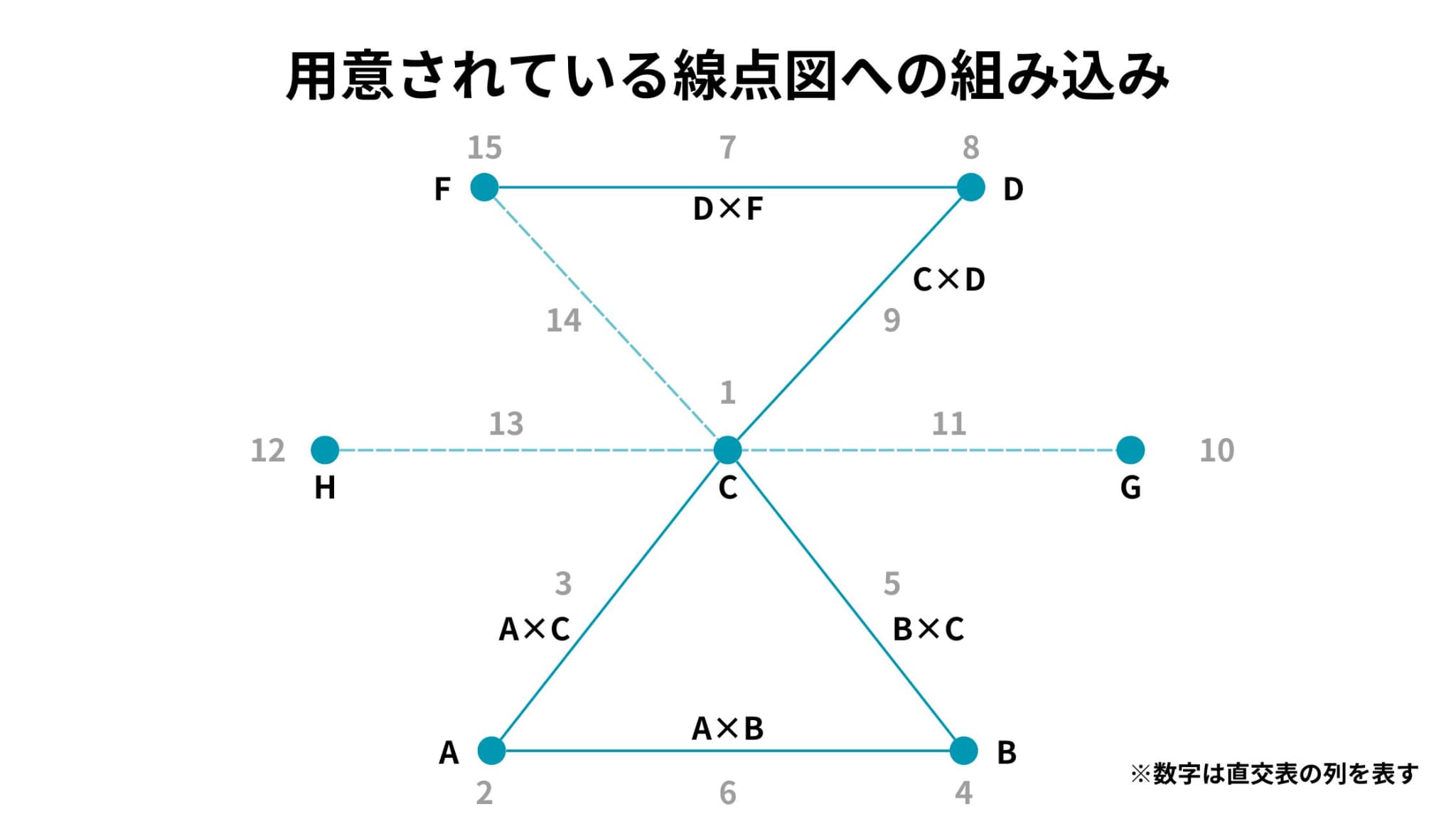
この線点図をもとにL16直交表への割り付けとデータの測定(実験)を行った結果、以下のような表が得られました。
なお、実験順序はランダムです(無作為化の原則)。
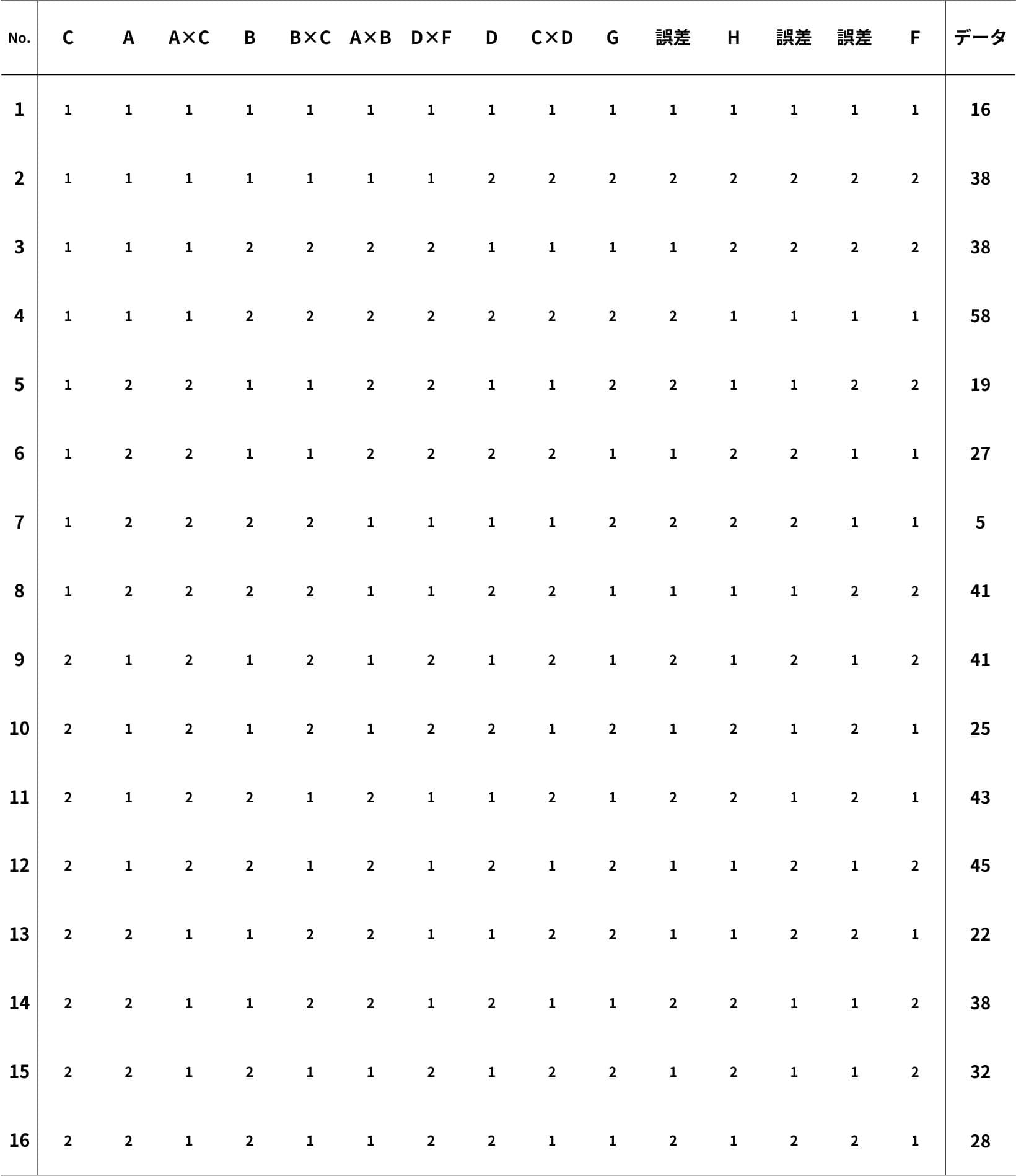
また、直交表では、因子が割り付けられておらず、検討すべき交互作用も現れない列を誤差列と呼びます。
平方和の計算
分散分析における一元配置法や二元配置法と同様、平方和を計算していきます。
ただし、2水準系の場合にはより簡単な形で計算することができます。
それが、直交表特有の列平方和と呼ばれるものです。
第[\(k\)]列が第\(i\)水準のデータ和を\(T_{[k]_{i}}\)、第[\(k\)]列が第\(i\)水準のデータ数を\(N_{[k]_{i}}\)、第[\(k\)]列が第\(i\)水準のデータの平均を\(\bar x_{[k]_{i}}\)とすると、第[\(k\)]列に対する列平方和は以下のように定義できます。
(第[\(k\)]列の列平方和)=\(\displaystyle S_{[k]}=\frac{(T_{[k]_{1}}-T_{[k]_{2}})^2}{N}\)
今回の例であれば、因子Cを第1列に割り付けていますから、\(T_{C_{1}}=T_{[1]_{1}}\)、\(T_{C_{2}}=T_{[1]_{2}}\)であり、\(S_{C}=S_{1}\)となります。
つまり、直交表を用いた解析では、因子の平方和はその因子を割り付けた列の列平方和と対応すると言えます。
また、列平方和に対して列自由度を考えることができます。
それぞれの列には2水準が設定されているため、以下のように定義できます。
(第[\(k\)]列の列自由度)=\(\phi_{[k]}=2-1=1\)
さらに、L16直交表では、以下の2つの式が成り立ちます。
総平方和: \(S_{T}=S_{[1]}+S_{[2]}+S_{[3]}+\cdots+S_{[15]}\)
総自由度: \(\phi_{T}=\phi_{[1]}+\phi_{[2]}+\phi_{[3]}+\cdots+\phi_{[15]}\)
このことから、2水準系直交表では、総平方和\(S_{T}\)を自由度が1ずつの平方和に分解していると言えます。
分散分析表の作成
さて、平方和の算出方法がわかったので、それぞれの主効果および交互作用、誤差の平方和を計算し、分散分析表を作成していきます。
作成した分散分析表がこちら。
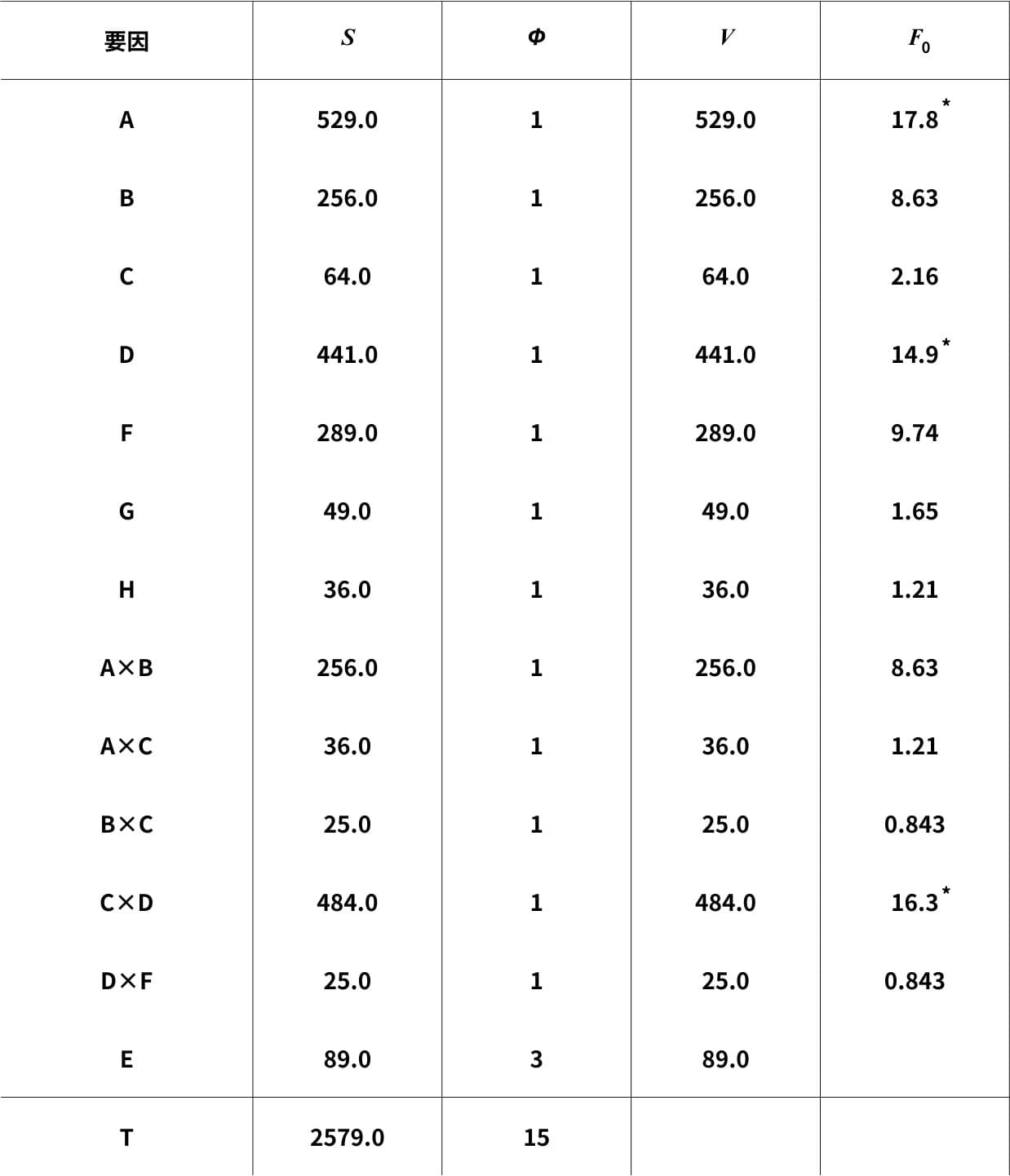
\(F(1,3;0.05)=10.1\)、\(F(1,3;0.01)=34.1\)より、因子A、Dと交互作用C×Dが有意であることがわかりました。
有意差については以下の記事で解説しています!

プーリング
分散分析表を見ると、\(F_{0}\)が小さい、つまり効果がない因子や交互作用がいくつかあることがわかります。
そこで、それらを誤差と見なし、再度分散分析表を作成していきます。
この作業のことをプーリングと呼びます。
プーリングを行うことで、誤差の自由度が増え、誤差分散の推定精度が上がります。
プーリングの絶対的な基準は存在しませんが、慣例的に用いられているルールには以下のようなものがあります。
① \(F_{0}\leq 1\)のときは誤差項にプールする
② \(1<F_{0}<F(0.05)\)のとき、すなわち有意ではないが\(F_{0}\)が1以下ではないときは、技術的に検討して処理方法を決める
③ \(F_{0}\geq F(0.05)\)のとき、すなわち有意なときはプールしない
今回の例では、\(F_{0}\)の小さなG、H、A×C、B×C、D×Fをプールして新たな分散分析表を作成していきます。
因子Cの\(F_{0}\)は微妙な大きさですが、C×Dが既に有意であるため、プールはしません。
プーリング後の分散分析表がこちら。
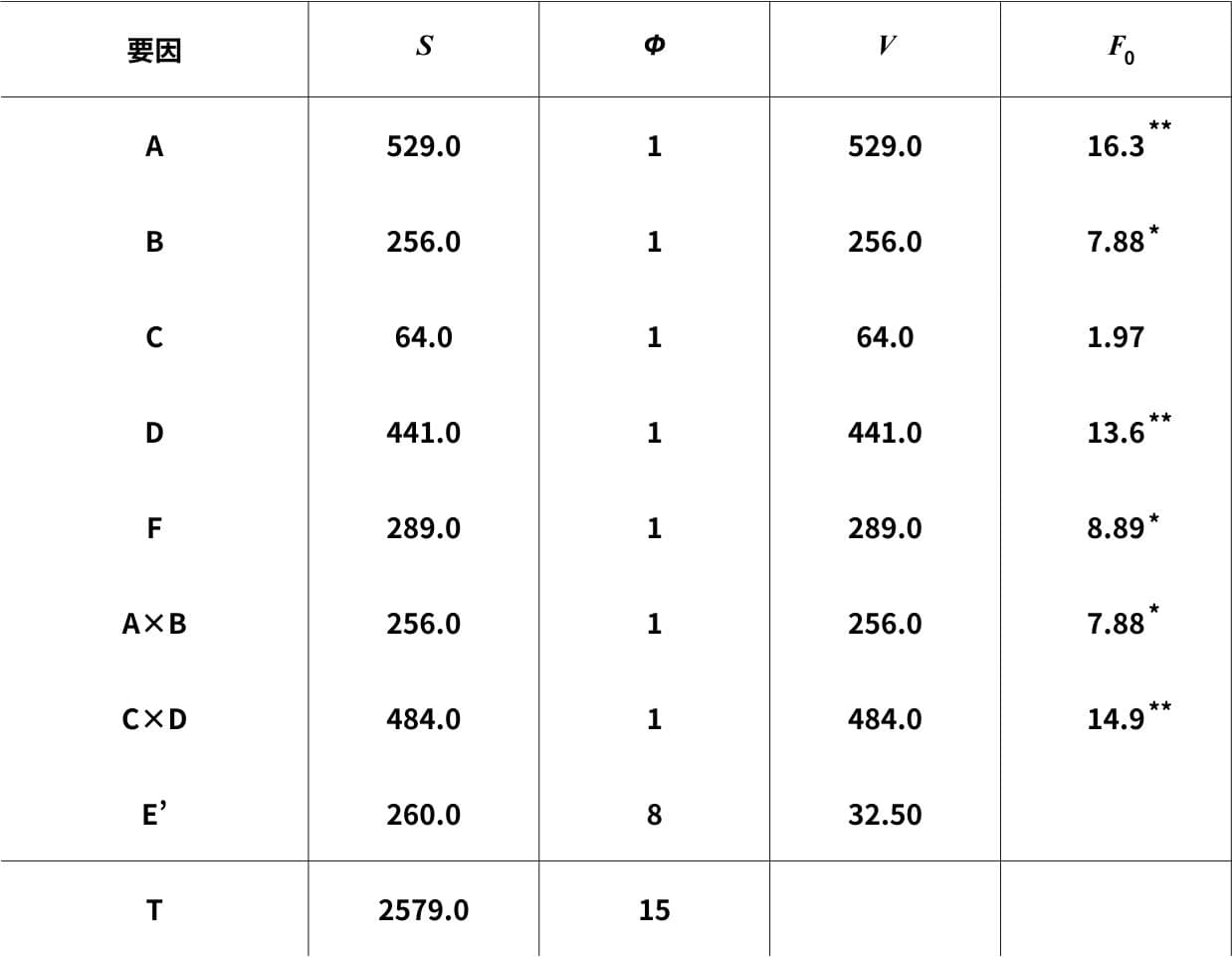
\(F(1,8;0.05)=5.32\)、\(F(1,8;0.01)=11.3\)より、因子A、Dと交互作用C×Dが高度に有意になり、因子B、Fと交互作用A×Bが有意になりました。
最適水準の決定
分散分析表(プーリング後)より、今回のデータの構造式は以下のように考えることができます。
\(x=\mu +a+b+c+d+f+(ab)+(cd)+\varepsilon\)
この構造式より、因子A、B、C、D、Fの水準組み合わせの下での母平均の推定値は、以下の式で表すことができます(\(\hat{}\)は推定値であることを示しています)。
\(\hat{\mu}(ABCDEF)\)
\(=\hat{(\mu +a+b+(ab))}+\hat{(\mu +c+d+(cd))}+\hat{(\mu +f)}-2\hat{\mu}\)
\(=\bar{x}_{AB}+\bar{x}_{CD}+\bar{x}_{F}-2\bar{\bar{x}}\)
この式を最大にする因子の水準は、それぞれの2因子の2元表を作成することで確かめることができます。
例えば因子AとBの2元表は以下のようになります。

表より、A1B2の平均値が最も大きな値であることがわかります。
よって、因子A、Bの最適水準はA1B2となります。
同様にして、因子C、DはC1D2、因子FはF2が最適水準となります。
実験計画法をPythonでやってみよう

ここからは、Pythonで実際に実験計画法をやっていきます(実務では解析ソフトなどが使われることが多いです)!
適用例でも紹介した、直交表を用いた実験計画法をやっていきましょう。
分析の目的は、最もよい水準を見つけること!
以下の流れで分析を進めていきます。
1. ライブラリのインストール
2. データの準備
3. 列平方和と自由度の算出
4. 分散分析表の作成
5. 最適水準の決定
1. ライブラリのインストール
今回はscipyのstatsを使って分散分析(\(F\)値の算出)を行っていきます。
分析で使用する他のモジュール等もここで全てimportしておきます。
import pandas as pd
import numpy as np
from scipy.stats import f2. データの準備
今回は因子A~D(各2水準)と交互作用A×Bを取り上げます。
そのため、L8直交表を用いることにします。
直交表への割り付けとデータの測定を既に終えたとして、直交表を表示します。
なお、今回のデータは値が大きいほど良いものとします。
#因子A~D
#因子は全て2水準ずつ
#技術的観点から、交互作用はA×Bのみ存在するとした
#L8直交表への割り付け
A = np.array([1,1,1,1,2,2,2,2]) #因子A
B = np.array([1,1,2,2,1,1,2,2]) #因子B
A_B = np.array([1,1,2,2,2,2,1,1]) #交互作用A×B
C = np.array([1,2,1,2,1,2,1,2]) #因子C
D = np.array([1,2,1,2,2,1,2,1]) #因子D
E_1 = np.array([1,2,2,1,1,2,2,1]) #誤差列
E_2 = np.array([1,2,2,1,2,1,1,2]) #誤差列
#直交表をデータフレームとして表示
L8_array = pd.DataFrame({
'A':A,
'B':B,
'A-B':A_B,
'C':C,
'D':D,
'E1':E_1,
'E2':E_2,
'データ':np.array([65,89,76,91,33,37,48,43])
})
#見やすさのため、行番号を1からに変更
L8_array.index = [i for i in range(1,len(L8_array)+1)]
L8_array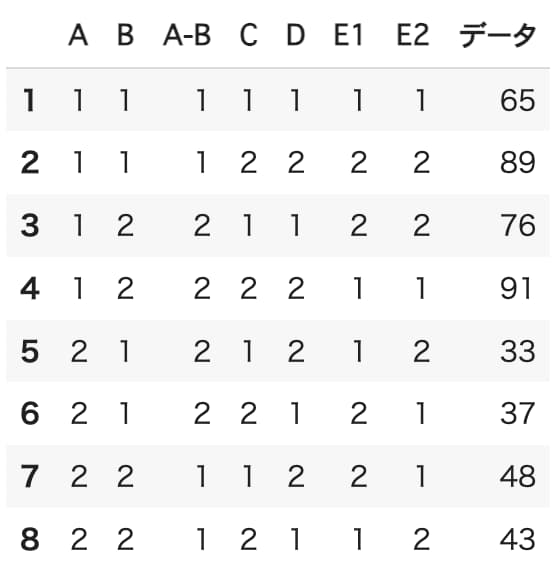
3. 列平方和と自由度の算出
続いて、列平方和と自由度をそれぞれ算出しておきます。
また、この後扱いやすくするため、それぞれリストにまとめておきます。
#各列の平方和を計算
S_A = (sum(L8_array.query('A==1')['データ'].values)-sum(L8_array.query('A==2')['データ'].values))**2/8
S_B = (sum(L8_array.query('B==1')['データ'].values)-sum(L8_array.query('B==2')['データ'].values))**2/8
S_AB = (sum(L8_array.query('A-B==1')['データ'].values)-sum(L8_array.query('A-B==2')['データ'].values))**2/8
S_C = (sum(L8_array.query('C==1')['データ'].values)-sum(L8_array.query('C==2')['データ'].values))**2/8
S_D = (sum(L8_array.query('D==1')['データ'].values)-sum(L8_array.query('D==2')['データ'].values))**2/8
S_E1 = (sum(L8_array.query('E1==1')['データ'].values)-sum(L8_array.query('E1==2')['データ'].values))**2/8
S_E2 = (sum(L8_array.query('E2==1')['データ'].values)-sum(L8_array.query('E2==2')['データ'].values))**2/8
S_E = S_E1 + S_E2
S_T = sum([S_A, S_B, S_C, S_D, S_AB, S_E]) #総平方和
S_list = [S_A, S_B, S_C, S_D, S_AB, S_E, S_T] #リストにまとめておく
#各列の自由度をリストにまとめておく
deg_list = [1,1,1,1,1,2,7]4. 分散分析表の作成
続いて、算出した列平方和および自由度をもとに、分散分析表を作成していきます。
さらに有意であるかどうかを判断するため、F分布の5%点および1%点を表示しておきます。
#分散の計算
V = [x / y for (x, y) in zip(S_list,deg_list)]
#F0の計算
F0 = [x/V[5] for x in V]
#分散分析表の作成
ANOVA_table = pd.DataFrame({
'S':S_list,
'Φ':deg_list,
'V':V,
'F0':F0
})
#行名を要因名に変更
index_name = ['A','B','C','D','A×B','E','T']
ANOVA_table.index = index_name
#分散分析表として表示するため、不要のセルには欠損値を格納
ANOVA_table.loc['T','V'] = None
ANOVA_table.loc['E','F0'] = None
ANOVA_table.loc['T','F0'] = None
ANOVA_table#分子、分母の自由度
dfn, dfd = 1, 2
#5%点(上側なので、95% を指定)
five = f.ppf(0.95, dfn, dfd)
print('上側確率 5%:', five)
#1%点(上側なので、99% を指定)
one = f.ppf(0.99, dfn, dfd)
print('上側確率 1%:', one)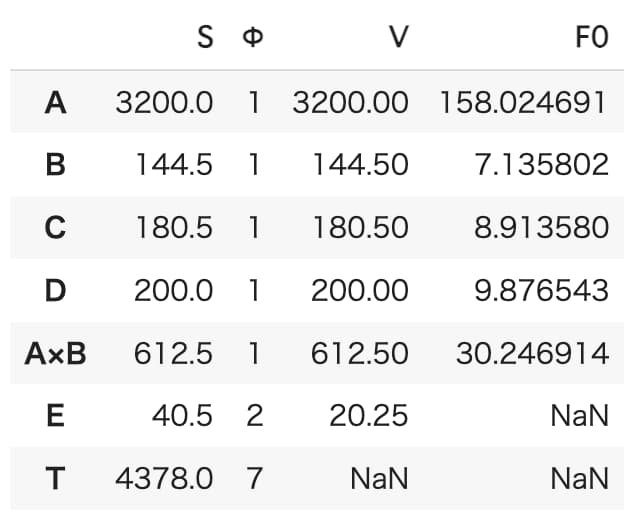

よって、因子Aは高度に有意であり、交互作用A×Bも有意であることがわかりました。
なお、今回はプーリングは行わないこととします。
5. 最適水準の決定
最後に、最適水準の決定を行います。
有意であるのは因子Aと交互作用A×Bであったため、因子AとBの最適水準を求めます。
上の適用例で説明したように、AB二元表を作成し、最適水準を決定します。
#優位となったのは因子A、交互作用A×B
#交互作用が有意となったので因子Bも取り上げる
#各水準組み合わせのときのデータの平均値を算出
Mean_A1B1 = sum(L8_array.query('A==1 & B==1')['データ'].values)/2 #A1とB1
Mean_A1B2 = sum(L8_array.query('A==1 & B==2')['データ'].values)/2 #A1とB2
Mean_A2B1 = sum(L8_array.query('A==2 & B==1')['データ'].values)/2 #A2とB1
Mean_A2B2 = sum(L8_array.query('A==2 & B==2')['データ'].values)/2 #A2とB2
#AB二元表の作成
AB_table = pd.DataFrame(
np.array([[Mean_A1B1,Mean_A1B2],
[Mean_A2B1,Mean_A2B2]]),
index = ['A1','A2'],
columns = ['B1','B2']
)
AB_table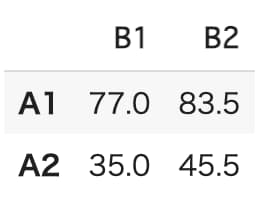
AB二元表より、A1B2の水準組み合わせのとき、最もデータの平均値が大きくなっていることがわかります。
よって、最適水準はA1B2であると言えます。
実験計画法 まとめ
ここまでご覧いただきありがとうございました!
本記事では、実験計画法の概要からPythonでの実装方法まで解説していきました。
実験計画法の主な使用場所は品質管理の現場ですが、この考え方は様々な場所で応用することができます。
複数の要因の効果を効率よく調べたい場合は、ぜひ実験計画法を使ってみましょう!
また、今回分析に用いたPythonについて勉強したい方は以下の記事を参考にしてみてください!

さらに詳しくAIやデータサイエンスの勉強がしたい!という方は当サイト「スタビジ」が提供するスタビジアカデミーというサービスで体系的に学ぶことが可能ですので是非参考にしてみてください!
AIデータサイエンス特化スクール「スタアカ」

| 【価格】 | ライトプラン:1280円/月 プレミアムプラン:149,800円 |
|---|---|
| 【オススメ度】 | |
| 【サポート体制】 | |
| 【受講形式】 | オンライン形式 |
| 【学習範囲】 | データサイエンスを網羅的に学ぶ 実践的なビジネスフレームワークを学ぶ SQLとPythonを組み合わせて実データを使った様々なワークを行う マーケティングの実行プラン策定 マーケティングとデータ分析の掛け合わせで集客マネタイズ |
データサイエンティストとしての自分の経験をふまえてエッセンスを詰め込んだのがこちらのスタビジアカデミー、略して「スタアカ」!!
当メディアが運営するスクールです。
24時間以内の質問対応と現役データサイエンティストによる複数回のメンタリングを実施します!
カリキュラム自体は、他のスクールと比較して圧倒的に良い自信があるのでぜひ受講してみてください!
他のスクールのカリキュラムはPythonでの機械学習実装だけに焦点が当たっているものが多く、実務に即した内容になっていないものが多いです。
そんな課題感に対して、実務で使うことの多いSQLや機械学習のビジネス導入プロセスの理解なども合わせて学べるボリューム満点のコースになっています!
Pythonが初めての人でも学べるようなカリキュラムにしておりますので是非チェックしてみてください!
ウォルマートのデータを使って商品の予測分析をしたり、実務で使うことの多いGoogleプロダクトのBigQueryを使って投球分析をしたり、データサイエンティストに必要なビジネス・マーケティングの基礎を学んでマーケティングプランを作ってもらったり・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践してもらったりする盛りだくさんの内容になってます!
・BigQuery上でSQL、Google Colab上でPythonを使い野球の投球分析
・世界最大手小売企業のウォルマートの実データを用いた需要予測
・ビジネス・マーケティングの基礎を学んで実際の企業を題材にしたマーケティングプランの策定
・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践して稼ぐ