分散分析についてわかりやすく解説!Pythonで実装してみよう!

こんにちは!スタビジ編集部です!
ある事象の仮説を数理的に確かめるために行われる統計的検定。
統計学の基本であり、様々なところで用いられている有用な手法です。
そんな統計的検定の考え方を用いる分析はいくつかありますが、この記事ではその中でも最も基本的な分析である分散分析について解説していきます。
分散分析に関しては以下の動画でもわかりやすく解説していますのであわせてチェックしてみてください!
目次
分散分析とは

分散分析とは、その名の通りデータの「分散」をもとに行う分析手法です。
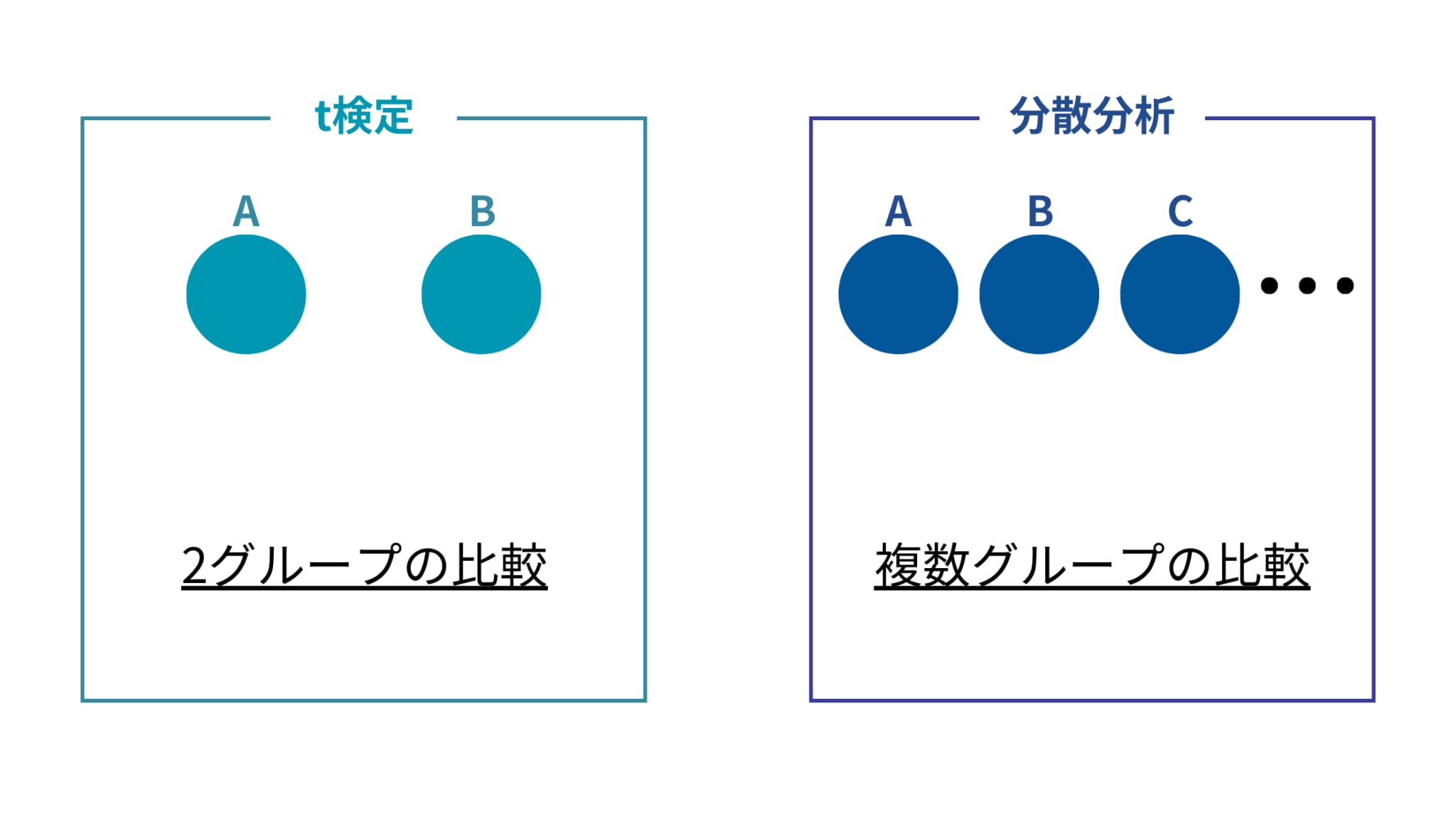
その目的は、ズバリ「複数のグループの平均の違いを検定する」こと!
例えば、A,B,Cの3クラス(生徒20人ずつ)に対して数学のテストを行ったとしましょう。
なお、数学担当の教師はそれぞれのクラスで異なるとします。
その結果、以下のような得点表が得られました。
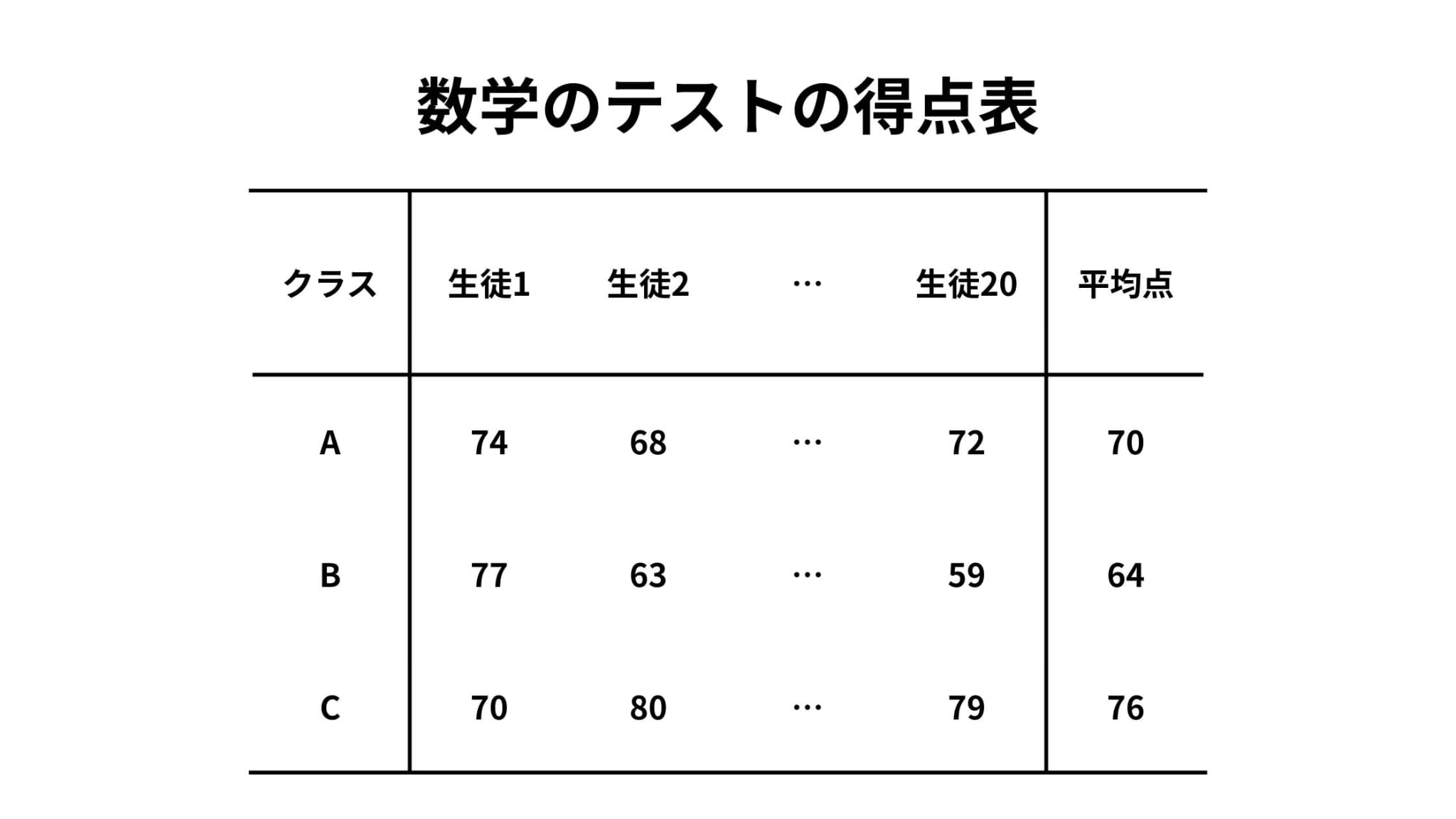
表を見ると、各クラスの平均点が異なることがわかります。
しかし、この得点表だけで「数学担当教師の違いにより、各クラスの平均点が異なる」と結論づけることはできません。
なぜなら、各クラスの平均点の差が統計的に意味のある差なのかがわからないからです。
また、平均点の差が数学担当教師の違いによるものであるかどうかも定かではありません。
そこで、分散分析を用いて統計的に解析し、判断を下すというわけです。

分散分析の理論と手順

分散分析の理論と手順について、先ほどの数学のテストの例を用いて説明していきます。
1. ばらつきの分解
各生徒の数学のテストの得点をプロットすると、以下のような図ができます。
なお、図中の✖️は各クラスの平均値を表しています。

この図を見てみると、全体として、得点はおよそ60点から90点までの間をばらついていることがわかります。
なぜばらついているのかというと、もちろん、数学担当教師の違いが原因としてあげられます。
数学担当教師の教え方に差があれば、クラスとしての数学力の差にも違いが生じますからね。
しかし、同じクラスであっても得点がばらついていることがわかります。
その原因としては、個人ごとの数学力の差や今回のテスト問題に対する得意・不得意など、様々なものが考えられます。
しかし、そのようなばらつきの原因を全て把握するというのは現実問題として不可能であり、非効率的です。
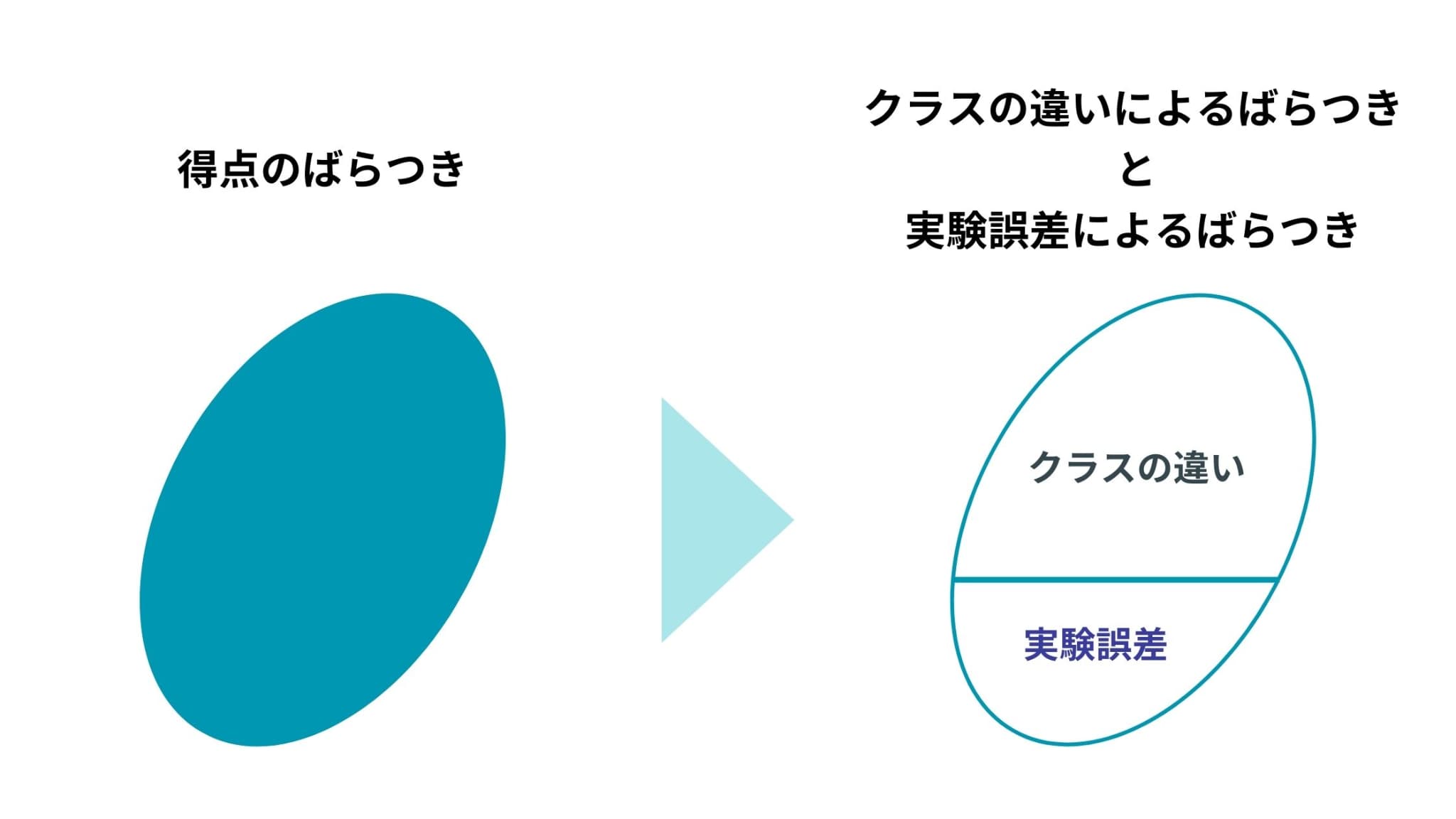
そこで、数学担当教師の違い以外による、ばらつきの様々な原因を併せたものを実験誤差として考えていきます。
つまり、データのばらつきを「数学担当教師(クラス)の違いによるばらつき」と「それ以外の実験誤差によるばらつき」の2つに分けて考える、ということです。
これが分散分析の基本的な考え方です。
続いて、ばらつきの分解方法を見ていきます。
まず、各生徒の点数データを\(x_{ij}\)とします。ここで、クラスA,B,Cをクラス1,2,3とし、添字\(i\)はクラス(\(i=1,2,3\))を、添字\(j\)は生徒番号(\(j=1,2,…,20\))を表します。
また、全点数データの平均を\(\bar{\bar{x}}\)と表します。
さらに、各クラスごとの点数データの平均を\(\bar{x}_{i.}\)と表します。
これらを用いて、データのばらつきを以下の数式で表すことができます。
総平方和 : \(\displaystyle S_{T}=\sum_{i=1}^{3}\sum_{j=1}^{20}(x_{ij}-\bar{\bar{x}})^2\)
総平方和は、個々のデータと全平均との違いを2乗し、全てのデータについて足し合わせたもの(=全データのばらつき度合い)を示しています。
群間平方和 : \(\displaystyle S_{A}=\sum_{i=1}^{3}\sum_{j=1}^{20}(\bar{x}_{i.}-\bar{\bar{x}})^2\)
群間平方和は、クラス\(i\)における平均と全平均の違いを2乗し、全てのデータについて足し合わせたもの(=それぞれのクラスによるばらつき度合い)を示しています。
群内平方和 : \(\displaystyle S_{E}=\sum_{i=1}^{3}\sum_{j=1}^{20}(x_{ij}-\bar{x}_{i.})^2\)
群内平方和は、個々のデータとそれの属するクラス\(i\)における平均との違いを2乗し、全てのデータについて足し合わせたもの(=誤差によるばらつき度合い)を示しています。
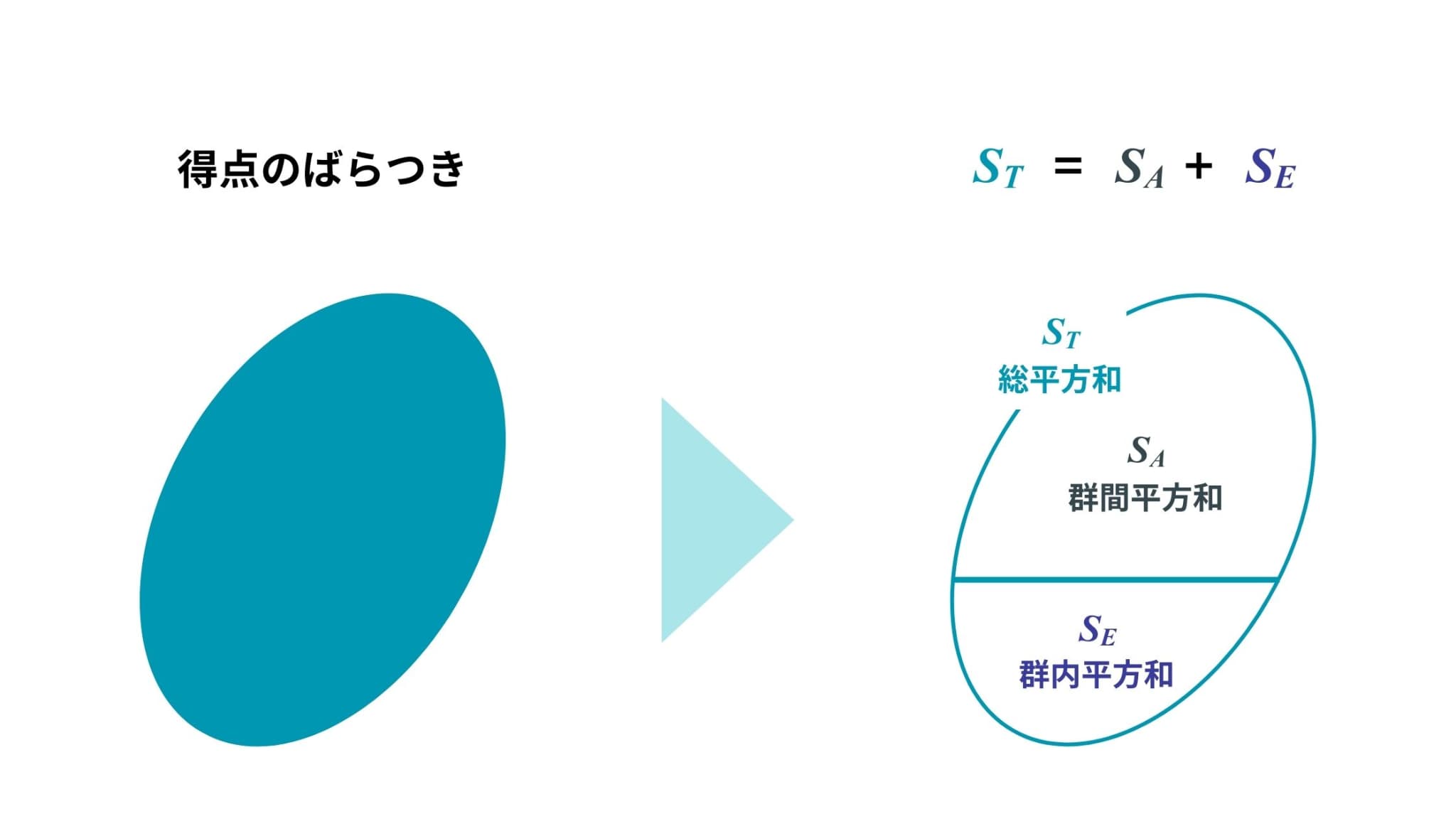
そして、上の3つの平方和の間には以下の関係が成り立ちます。
\(S_{T}=S_{A}+S_{E}\)
つまり、分散分析の考え方を数式を用いて表すと、以下の図のようになります。
2. 検定
ばらつきの分解により、全データのばらつきをクラスの違いによるばらつき(群間平方和)と誤差によるばらつき(群内平方和)の2つに分けることができました。
ここから、そのばらつきの大きさを、検定を用いて比較していきます。
検定のための準備として、群間平方和、群内平方和をそれぞれの自由度で割り、分散の形にしておきます。
各自由度の算出方法は以下の通りです。
全データの自由度 : \(\phi_{T}=(全データ数)-1\)
水準の自由度 : \(\phi_{A}=(水準数)-1\)
誤差の自由度 : \(\phi_{E}=\phi_{T}-\phi_{A}\)
それぞれの分散は以下のように表すことができます。
群間分散 : \(\displaystyle V_{A}=\frac{S_{A}}{\phi_{A}}\)
群内分散 : \(\displaystyle V_{E}=\frac{S_{E}}{\phi_{E}}\)
そして、分散比\(F_{0}\)を算出します。
分散比 : \(\displaystyle F_{0}=\frac{V_{A}}{V_{E}}\)
これまで算出してきた様々な値をまとめると、以下のような表を作成することができます。
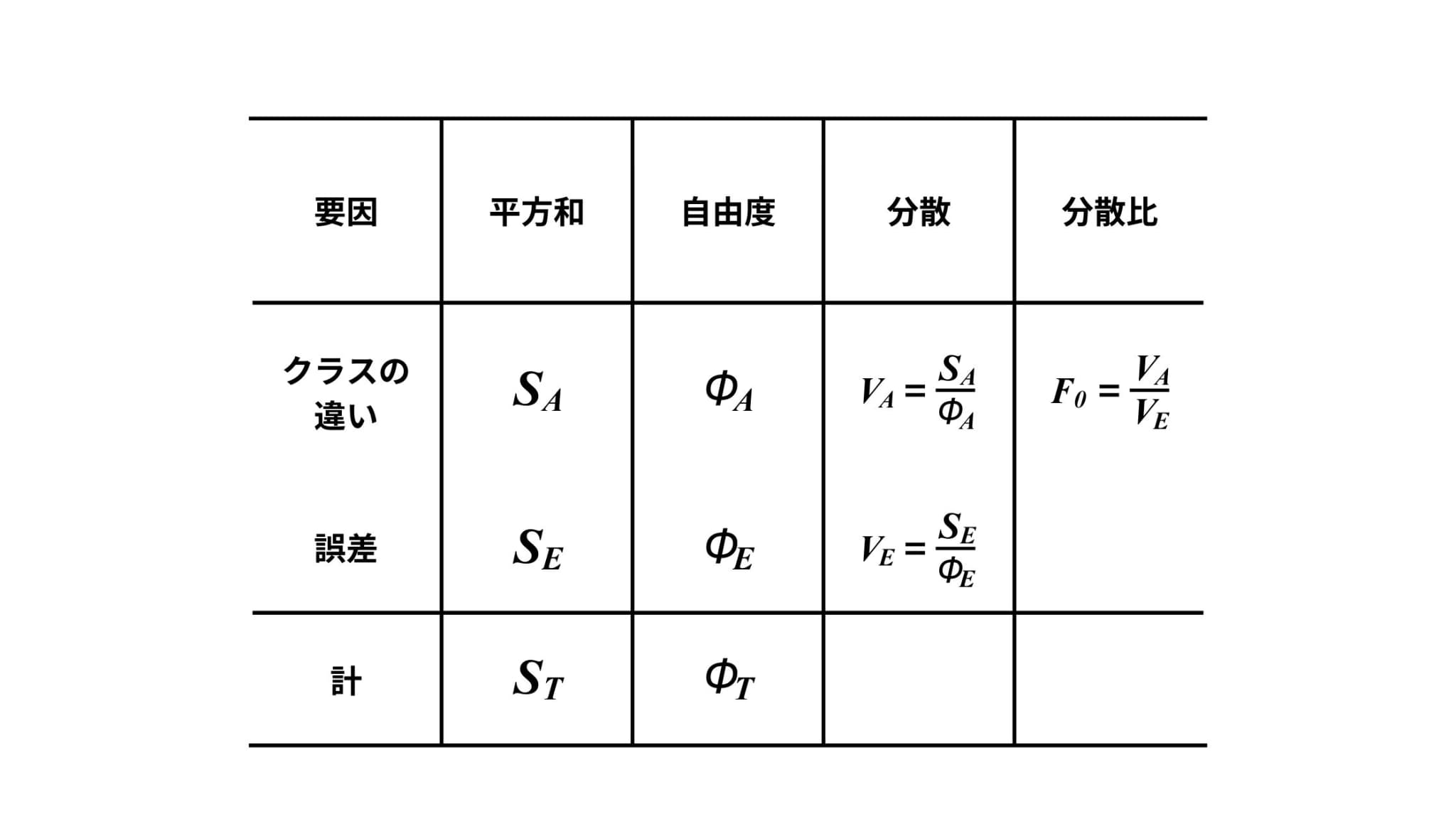
これは分散分析表と呼ばれるもので、分散分析の際はこのような表にまとめていきながら分析を進めていくことが多いです。
そして、分散比\(F_{0}\)の値を用いて検定を行います。
ここで用いる検定はF検定と呼ばれるものです。
検定の結果、\(F_{0}\)が\(F(\phi_{A},\phi_{E};\alpha)\)(\(\alpha\)はふつう0.05または0.01)以上の値であれば有意と判定し、クラスの違いにより平均点数が異なると結論づけることができます。


分散分析の種類

ここまで分散分析の理論を説明してきましたが、実は分散分析には以下の3つの種類があります。
1. 一元配置法
2. 二元配置法
3. 多元配置法
分析手順はほとんど変わりませんが、それぞれについて簡単に説明していきます。
1. 一元配置法
これは上の例で説明したような、因子が1つの場合の分散分析のことを言います。
一元配置法におけるデータの構造式は以下のように表すことができます。
\(x_{ij}=\mu+\alpha_{i}+\varepsilon_{ij}\)
この式は、個々のデータ\(x_{ij}\)は、全体の平均\(\mu\)に因子Aの効果\(\alpha_{i}\)と誤差\(\varepsilon_{ij}\)が加わったものであるということを示しています。
なお、一元配置法では繰り返し数が異なっていても問題ありません。
ただし、群間平方和を算出する際にそれを考慮する必要があるので気をつけましょう。
2. 二元配置法
これは因子が2つの場合の分散分析のことを言います。
さらに二元配置法は、繰り返しがある場合と繰り返しがない場合の2つに分けることができます。
繰り返しのある二元配置法
繰り返しのある二元配置法におけるデータの構造式は以下のように表すことができます。
\(x_{ijk}=\mu+\alpha_{i}+\beta_{j}+(\alpha\beta)_{ij}+\varepsilon_{ijk}\)
この式は、個々のデータ\(x_{ijk}\)は、全体の平均\(\mu\)に因子Aの効果\(\alpha_{i}\)と因子Bの効果\(\beta_{j}\)、交互作用効果\((\alpha\beta)_{ij}\)と誤差\(\varepsilon_{ijk}\)が加わったものであるということを示しています。
ここで、交互作用について簡単に説明します。
交互作用とは、「因子Aの水準によってBの効果が変わること」です。
もっと簡単に言えば、「組み合わせ効果」です。
例えば、ある料理に砂糖をどんどん加えれば甘さが増していき、塩をどんどん加えれば塩辛さが増していきますね。
しかし、砂糖の中に少量の塩を加えることで、甘さがより引き立てられることが知られています。
このように、ある量(水準)同士の組み合わせで効果が大きくなる場合があり、それを交互作用と呼ぶのです。
繰り返しのある二元配置法においても、ばらつきを分解して考えていくという手順は変わりません。
ただし因子が1つ加わったことで、ばらつきの分解が若干異なります。
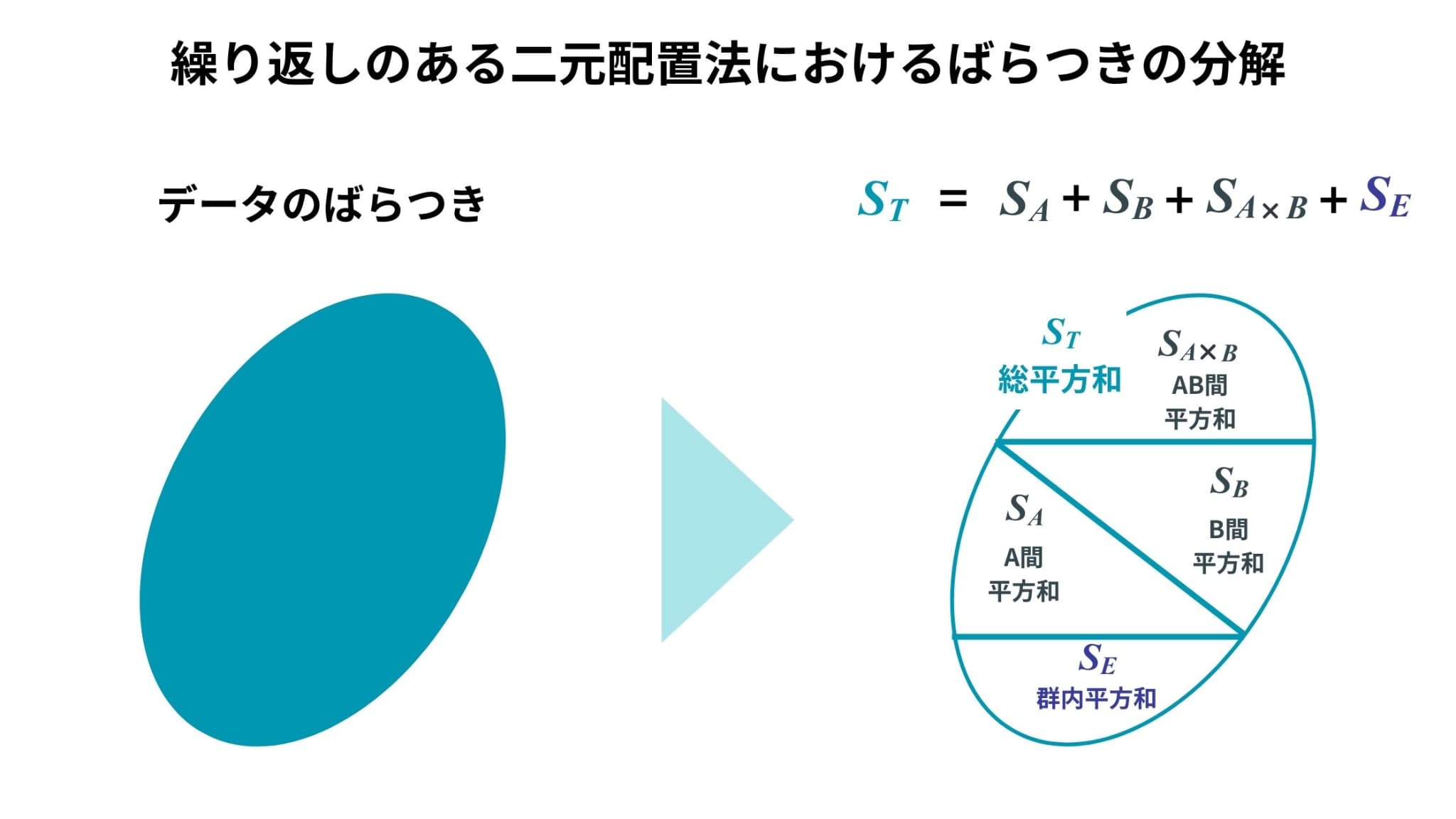
なお、繰り返しのある二元配置法では繰り返し数は揃えなければなりません。
繰り返しのない二元配置法
繰り返しのない二元配置法におけるデータの構造式は以下のように表すことができます。
\(x_{ij}=\mu+\alpha_{i}+\beta_{j}+\varepsilon_{ij}\)
この式は、個々のデータ\(x_{ij}\)は、全体の平均\(\mu\)に因子Aの効果\(\alpha_{i}\)と因子Bの効果\(\beta_{j}\)、誤差\(\varepsilon_{ij}\)が加わったものであるということを示しています。
そのため、繰り返しのない二元配置法ではあらかじめ交互作用がないことがわかっている場合に用いることがほとんどです。
また、先ほどと同様、ばらつきを分解して考えていくという手順は変わりませんが、ばらつきの分解が若干異なります。
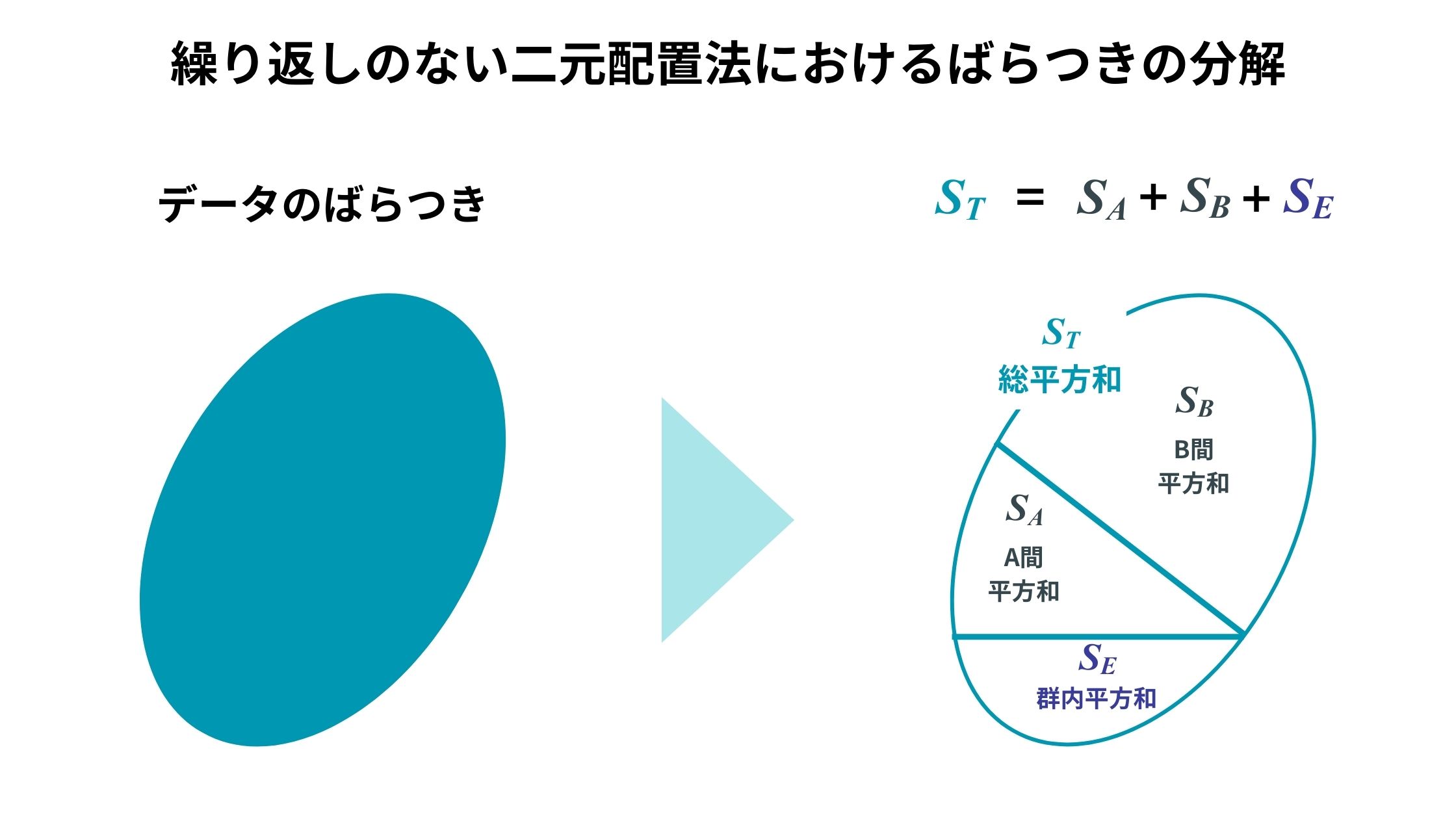
3. 多元配置法
これは因子が3つ以上の場合の分散分析のことを言います。
取り上げる因子が3つであれば三元配置法、4つであれば四元配置法となります。
さらに、二元配置法と同様、繰り返しがある場合とない場合の2つに分けることができます。
構造式などは省略しますが、例えば繰り返しのある三元配置法であれば、各因子の主効果の他に、因子AとB、BとC、AとC、AとBとCの4種類の交互作用を考慮する必要があります。
一方、繰り返しのない三元配置法であれば、交互作用は検出できません。
ばらつきの分解についても、二元配置法と同様です。
分散分析をPythonでやってみよう

ここからは、Pythonで実際に分散分析をやっていきます!
一番基本的な、繰り返しのある一元配置法をやっていきましょう。
分析の目的は、最もよい水準を見つけること!
以下の流れで分析を進めていきます。
1. ライブラリのインストール
2. データの準備
3. 分散分析の実行
1. ライブラリのインストール
今回はscipyのstatsを使って分散分析を行っていきます。
分析で使用する他のモジュール等もここで全てimportしておきます。
import pandas as pd
import numpy as np
from scipy import stats2. データの準備
今回は手元で作成したデータを使います。
ある因子A(4水準)を取り上げ、3回ずつの実験で計12個のサンプルが得られた場合を考えます。
値が高いほどよいサンプル、であるとします。
#因子A、4水準、繰り返し3
A_Level1 = np.array([2.0, 2.2, 2.1])
A_Level2 = np.array([2.4, 2.8, 2.6])
A_Level3 = np.array([2.1, 2.3, 2.6])
A_Level4 = np.array([2.0, 1.7, 2.0])
#データフレームにまとめる
data = pd.DataFrame({
'水準1' : A_Level1,
'水準2' : A_Level2,
'水準3' : A_Level3,
'水準4' : A_Level4
})
data = data.T #見やすいようにように転置
data['平均値']=data.T.mean(axis=0).values
data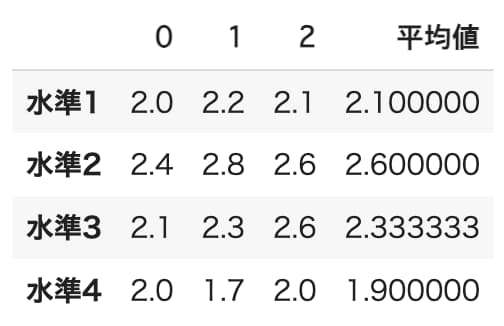
各水準の平均値に差があり、水準2の平均値が最も高いことがわかります。
ただ、これだけでは統計的に意味がある差なのかわかりません。
そのため、分散分析を行っていきます。
3. 分散分析(F検定)の実行
f_oneway関数を用いて、分散分析(F検定)を行います。
fvalue, pvalue = stats.f_oneway(data['水準1'], data['水準2'], data['水準3'], data['水準4'])
print(f"F-val:{fvalue:.4}, P-val:{pvalue:.4}")算出されたF値(分散比\(F_{0}\))が7.628であり、p値が0.009862であることを示しています。
p値が0.01を下回っていることから、高度に有意であることがわかります。
ゆえに、因子Aは水準ごとに違いがあり、最も良い水準(最適水準)は水準2であると言えます。
まとめ
今回は分散分析の概要からPythonでの実装方法まで解説していきました。
分散分析は、様々な場で活用することのできる手法です。
複数グループの違いを検証できるのはもちろんのこと、手法の理論を知っておくことで他の分析手法の理解が容易になります。
複数のグループとして観測されたデータが手元にある場合は、分析の第一歩として分散分析をぜひやってみましょう!
より分散分析について詳しく知りたい方には以下の書籍がオススメです。是非目を通してみてください!
■入門 統計解析法
統計学の基本を理解するのにうってつけの本です。基本的に高校レベルの数学ができれば問題なく理解できるレベル。大学生1~2年生の時に非常にお世話になりました。
また、今回分析に用いたPythonについて勉強したい方は以下の記事を参考にしてみてください!

さらに詳しくAIやデータサイエンスの勉強がしたい!という方は当サイト「スタビジ」が提供するスタビジアカデミーというサービスで体系的に学ぶことが可能ですので是非参考にしてみてください!
AIデータサイエンス特化スクール「スタアカ」

| 【価格】 | ライトプラン:1280円/月 プレミアムプラン:149,800円 |
|---|---|
| 【オススメ度】 | |
| 【サポート体制】 | |
| 【受講形式】 | オンライン形式 |
| 【学習範囲】 | データサイエンスを網羅的に学ぶ 実践的なビジネスフレームワークを学ぶ SQLとPythonを組み合わせて実データを使った様々なワークを行う マーケティングの実行プラン策定 マーケティングとデータ分析の掛け合わせで集客マネタイズ |
データサイエンティストとしての自分の経験をふまえてエッセンスを詰め込んだのがこちらのスタビジアカデミー、略して「スタアカ」!!
当メディアが運営するスクールです。
24時間以内の質問対応と現役データサイエンティストによる複数回のメンタリングを実施します!
カリキュラム自体は、他のスクールと比較して圧倒的に良い自信があるのでぜひ受講してみてください!
他のスクールのカリキュラムはPythonでの機械学習実装だけに焦点が当たっているものが多く、実務に即した内容になっていないものが多いです。
そんな課題感に対して、実務で使うことの多いSQLや機械学習のビジネス導入プロセスの理解なども合わせて学べるボリューム満点のコースになっています!
Pythonが初めての人でも学べるようなカリキュラムにしておりますので是非チェックしてみてください!
ウォルマートのデータを使って商品の予測分析をしたり、実務で使うことの多いGoogleプロダクトのBigQueryを使って投球分析をしたり、データサイエンティストに必要なビジネス・マーケティングの基礎を学んでマーケティングプランを作ってもらったり・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践してもらったりする盛りだくさんの内容になってます!
・BigQuery上でSQL、Google Colab上でPythonを使い野球の投球分析
・世界最大手小売企業のウォルマートの実データを用いた需要予測
・ビジネス・マーケティングの基礎を学んで実際の企業を題材にしたマーケティングプランの策定
・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践して稼ぐ
























