【5分で分かる】t検定の概要とPythonやRでのやり方紹介!

こんにちは!
データサイエンティストのウマたん(@statistics1012)です。
ある事象の仮説を数理的に確かめるために行われる統計的検定。
統計学の基本であり、様々なところで用いられている現場でも有用な手法です。
そんな統計的検定にはいくつか種類がありますが、この記事ではその中でも最も基本的な検定であるt検定について見ていきたいと思います。
以下の動画でもt検定を分かりやすく解説しています!
統計的検定については以下の記事をご覧ください!

また以下の動画でもt検定を含めた統計的検定を解説しています!
理論を見ていき、最終的にはPython・Rで実装を行っていきます。

目次
t検定とは

t検定とは、どのような手法なのでしょうか?t検定とは「平均」の検定とよく言われます。
・得られたサンプルデータが想定の値よりズレているのか
・AとBのサンプル群の母平均に差はあるのか
などといったことがt検定を行うことで分かります。ちなみにF検定は「分散の検定」、カイ二乗検定は「分布の検定」と思っていただけると分かりやすいと思います。
正直、t検定自体の実装は非常に簡単なのでイメージさえ持っていれば数式を覚える必要はありません。
t検定は平均に差が生じているか確かめるもの。しかし、何を持って差があるか判断すればよいでしょう?
この時、母集団と標本という考え方についておさえておきましょう!
統計学では、手元のデータから真のデータの構造を推定することが重要です。
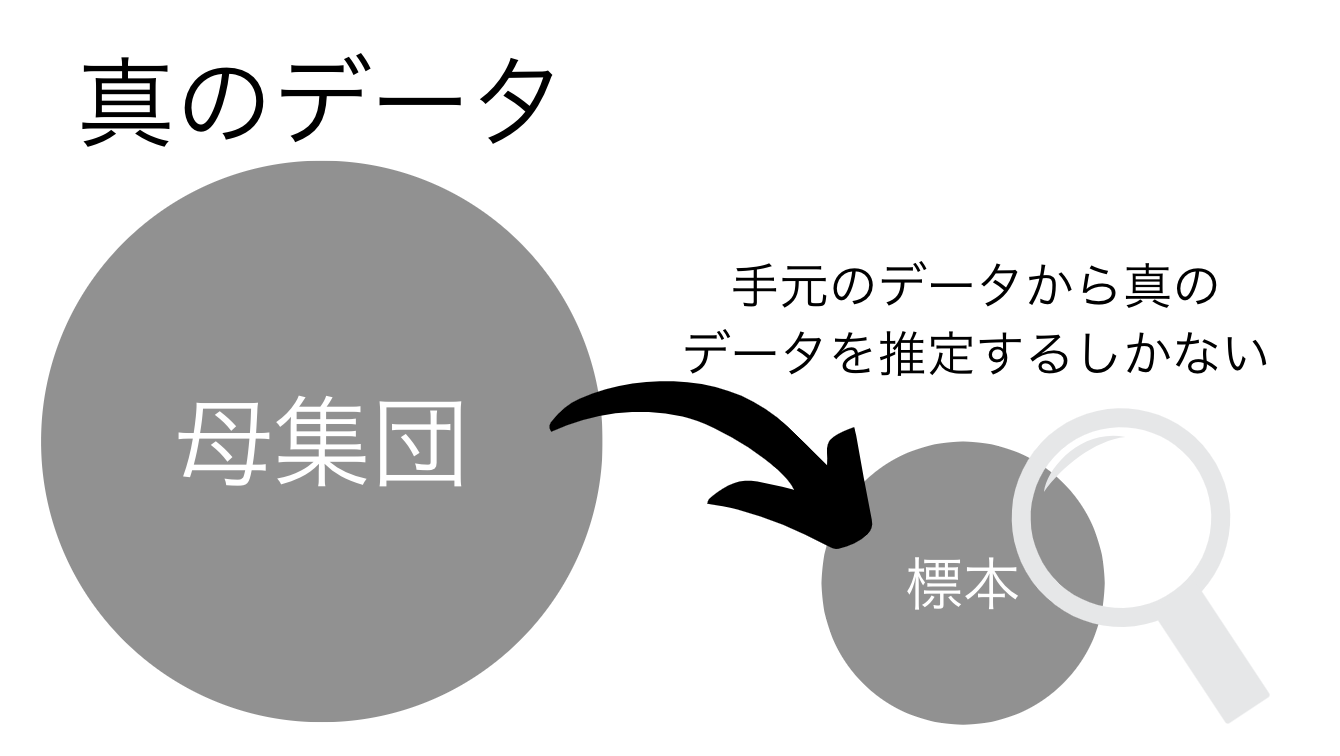
この時、母集団は真のデータを指していて、標本とは手元のデータを指しています。
そして母平均といえば母集団の真の平均、標本平均といえば標本の平均になります。
t検定では、標本平均から母平均を推定し、真の母平均とずれているかいないかを検定します。
では、単純に標本平均を算出して想定される母平均との差を求めればよいのでしょうか?
ここで重要なのが分散の観点とサンプル数の観点。
母平均が100で標本平均が120だったとしても、標本のデータが100、100、・・・10000、・・・、100だったしたら信頼性はありますか?あきらかに異常値が混ざっていることによって標本平均が上振れてしまっていますよね。
よって、分散が小さい方が信頼性は高くなるはずです。
また、手元のサンプルが10しかない状態と10000サンプルある状態ではどちらの方が信頼性が高いでしょう?
当たり前ですが10000サンプルですよね。このようにt検定においては分散の観点とサンプル数の観点が重要になってくるのです。
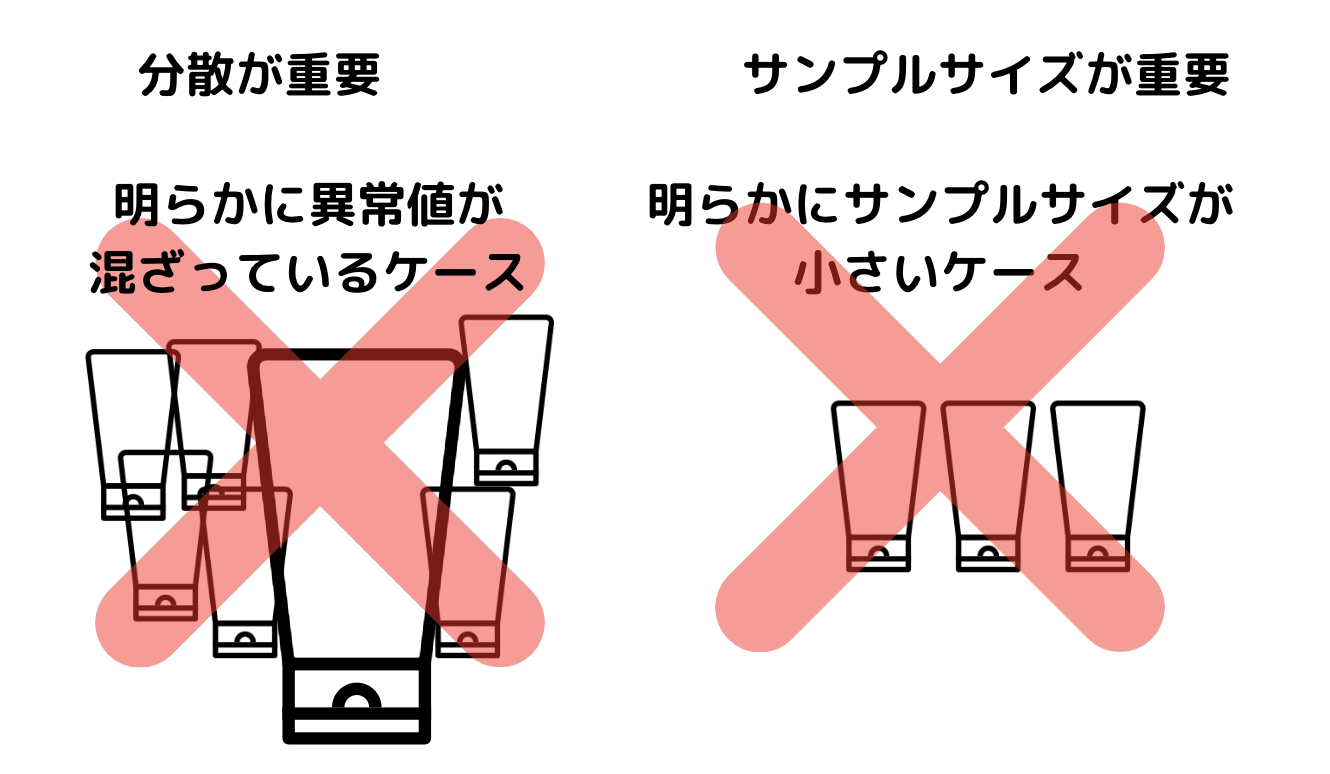
平均だけ算出して「差が出ました!!」と公言している資料などがありますが、t検定の考え方を知っていると、それ本当にサンプル数足りている?異常値混ざってない?と疑問が湧きます。
統計的検定では、このように表面的な事象に惑わされない本質的な検証が行えるのです。
・分散が小さい方が信頼性が高い
・サンプル数が大きい方が信頼性が高い
これらのイメージ・考え方をしっかり持っておくことで数式の理解も深まります。
ちなみにt検定はパラメトリック検定というデータの分布があらかじめ分かっている仮定のもとでの検定になります。
t検定の場合は正規分布を背後に仮定していますので正規分布と言えないデータ群には適応できない点に注意が必要です。
そんなt検定ですが、実はいくつかの種類があります。大きく分けて以下の3つ!
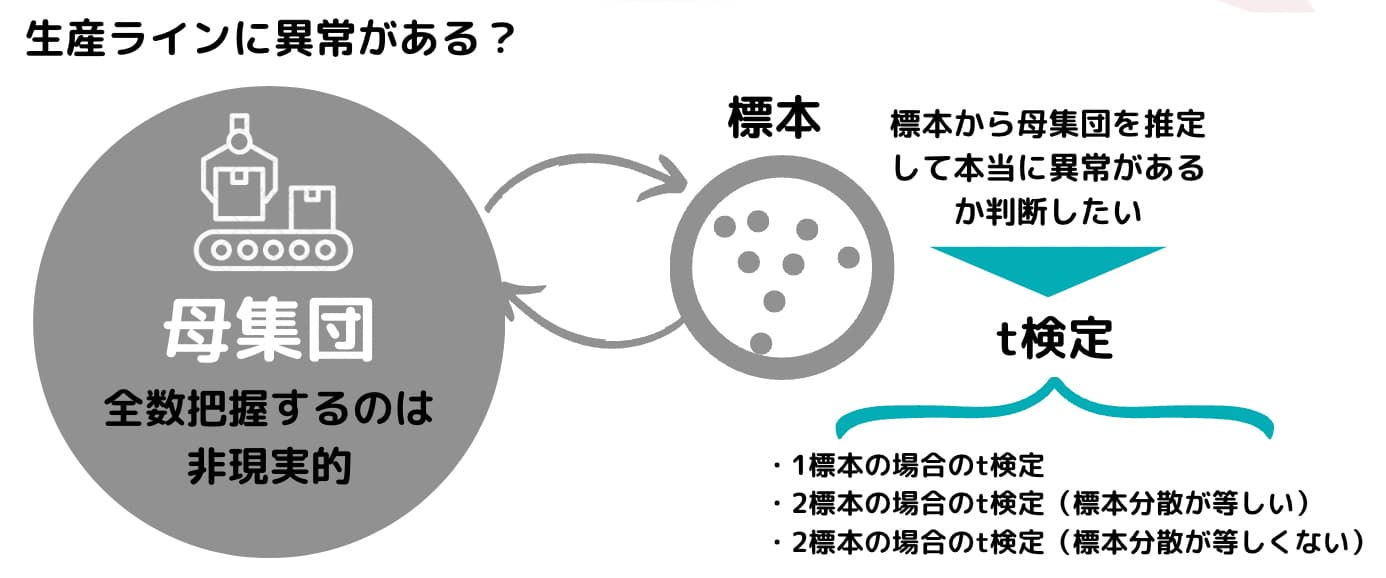
データの構造や検証した仮説によってt検定の中でも若干変わってくるんですね。
それぞれについて詳しく見ていくことにしましょう!
1標本の場合のt検定
こちらのパターンは品質管理の分野でよく用いられることが多いです。
得られたサンプルデータの母平均が想定している値に等しいかどうかを検定する場合に用います。サンプルデータが1つなので1標本というわけですね。
以下のような例を考えてみましょう!
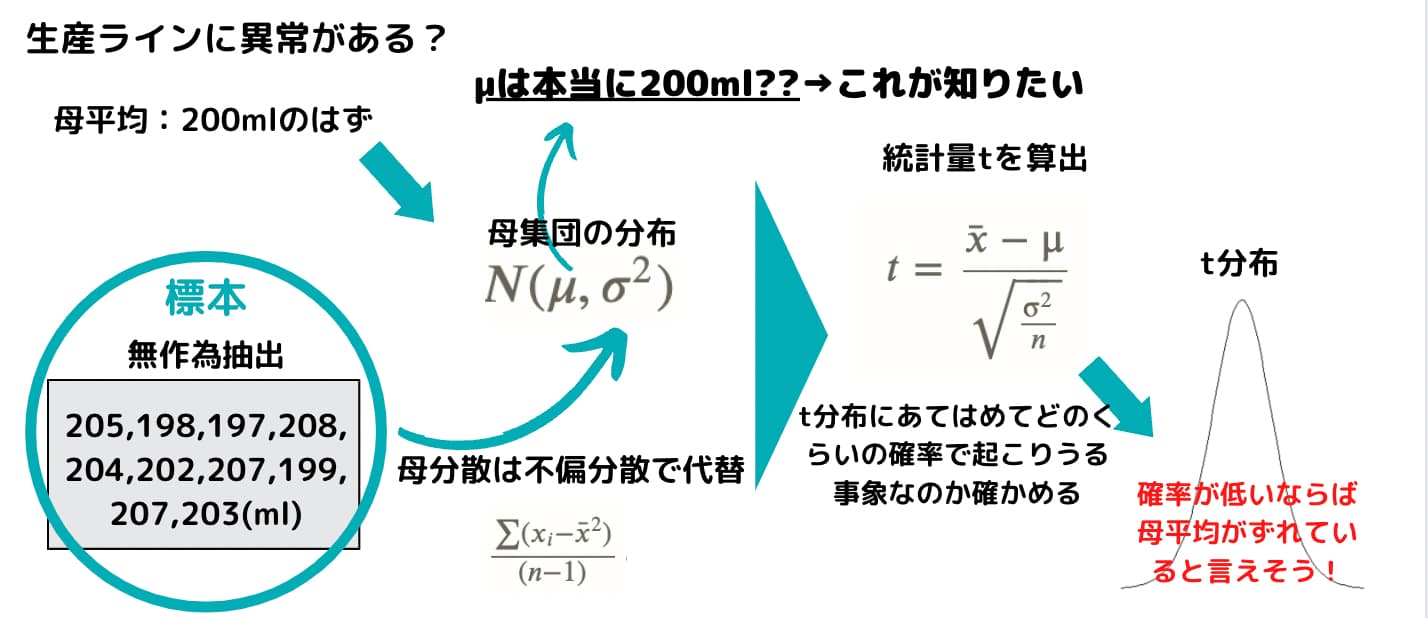
この会社が製造しているバニラアイスの内容量は200mlに設定しているはずです。
ある日、社長が「200mlになっていない気がする」と生産管理の担当者に伝えました。そこで、生産管理の担当者であるAさんとBさんは本当に200mlになっているかどうかを確かめることにしました。そして、製造した製品の中から無作為に10個ほど選んで内容量を測ったところ次のようになりました。
$$205,198,197,208,204,202,207,199,207,203 (ml)$$
このデータから平均値を計算すると\(\bar{x}=203\)でした。さて、設定は200mlからずれているのでしょうか。
まさに品質管理・生産管理の場面。
今回の場合、この時、母集団が母平均\(\mu\)母分散\(\sigma^2\)の正規分布に従っているとすると母集団は\(N(\mu,\sigma^2)\)に従っていると書くことができます。
不偏分散は\(\frac{{\sum}(x_i-\bar{x})^2}{(n-1)}\)と求めます。
そして、問題は\(\mu\)が200であるのかどうなのかということです。
ここで\(\mu=200\)であるとしましょう。標本平均\(\bar{x}=203\)と不偏分散から、tを以下のように求めます。
$$ t= \frac{\bar{x}-μ}{\sqrt{\frac{σ^2}{n}}} $$
この式はまさに先ほどの「平均との差」と「分散」と「サンプル数」が関係していますね!
平均との差が大きく分散が小さくサンプル数が大きい方がuの値は大きくなるはずです。
このtは自由度がn-1のt分布に従うことがわかっています。
自由度は分布の形を決めるもので、同じt分布でも自由度が大きければ大きいほど裾の狭い分布になっていきます。
さて、このtを計算してみると2.4となりました。
この2.4は自由度9のt分布に従います。
自由度9のt分布において2.4はどのくらいの確率で起きうるものなのでしょうか?
それを調べるにはt分布の表が必要です。今回は200mlより大きいかどうかという片側だけ検定すれば良いので片側t検定を用いましょう!
それを見てみると、有意差5%で自由度9の時の点は1.833であることが分かりました。
1.833より2.4は大きいので5%有意であるということが分かりました。
\(\mu=200\)と考えて、計算してみたところ、その結果計算するとたった5%も起こらないようなことになったということです。
ということは、もともと想定していた\(\mu=200\)つまり帰無仮説は間違っていたんじゃないの?というのが統計的検定の論理なんです。この5%というのは有意水準と呼ばれます。
今回は1.833を上回ったので有意であると判定されましたが、これが下回った場合は有意でないと言えるのでしょうか?
実は、ここが非常に難しいところで、このような場合「有意であるとは言えない」という結論しか導くことができません。
有意差については以下の記事で詳しくまとめていますのでそちらもあわせてご覧ください!

2標本の場合のt検定(分散が等しい)
先ほどの例では1標本のサンプルと想定される固定値を比較してt検定を行っていましたが、2標本のサンプルの母平均を比較する場合もあります。
その場合はどのようになるか見ていきましょう!
サンプルサイズ\(n,m\)の二つの標本、\(x_1,….,x_m\)と\(y_1,….,y_n\)が正規分布\(N(μ_1,σ_1^2)\)と\(N(μ_2,σ_2^2)\)に従うと仮定します。このとき、2標本の母平均には差があるのか検定を行います。帰無仮説と対立仮説は以下の通り。
帰無仮説\(H_0:\bar{x} = \bar{y}\)
対立仮説\(H_1:\bar{x} ≠ \bar{y}\)
この時、分散が等しい場合と等しくない場合では計算方法が異なります。母分散が等しいかどうかの検定にはWelch(ウェルチ)の検定を行います。
2標本の母分散が等しいと仮定した場合についてまず見ていきましょう!
\(x\)と\(y\)の不偏分散は等しく以下のように算出することができます。
$$ \hat{σ}^2 = \frac{Σ(x_i-\bar{x})^2+Σ(y_j-\bar{y})^2}{m + n -2}$$
この\(\hat{σ}\)を用いてt値を算出します。
$$t = \frac{\bar{x} – \bar{y}}{\sqrt{\frac{1}{m}+\frac{1}{n}}\hat{σ}} ~t(m + n – 2)$$
例の通り、平均の差と分散とサンプル数という要素が入っていますね!
2標本の場合のt検定(分散が等しくない)
続いて、分散が等しくない場合の例を見ていきましょう!
先ほどは\(\hat{σ}\)を共通の不偏分散として算出することができましたが、今回は異なるので別々に算出することになります。
$$ \hat{σ}_x^2 = \frac{Σ(x_i-\bar{x})^2}{m – 1} $$
$$ \hat{σ}_y^2 = \frac{Σ(y_i-\bar{y})^2}{n – 1} $$
これら固有の普遍分散を基にt値を算出します。
$$t = \frac{\bar{x} – \bar{y}}{\sqrt{\frac{\hat{σ}_x}{m}+\frac{\hat{σ}_y}{n}}}$$
ここでもやはり式は平均の差と分散とサンプル数で表されていますね!
回帰モデルにおけるt検定
実は、最も一般的でよく使われる回帰モデルにおいてもt検定が使われているのです。
よくある以下のような回帰モデル。
$$y_i=\beta_0+\beta_1x_{i1}+\cdots+\beta_px_{ip}+\epsilon_i, \epsilon_i \sim N(0,\sigma^2),(i=1,\cdots,n)$$
この時ある説明変数が目的変数に寄与しているかどうかは、\(\beta\)が0であるかどうかと言い換えることができます。
\(\beta\)が0であるかどうかをt検定によって導き出しているのです。
回帰分析については以下の記事で詳しくまとめています。

t検定をPythonで実装してみよう!

それなりに数式が多く初見の方にとっては難しく感じられたかもしれませんが、実はRやPythonなどのデータ分析言語を使えば一発で算出できちゃうんです!
まずは1標本のt検定をおこなっていきます。先程の例を元に実装してみましょう!
まず必要なライブラリをインポートしてきます
import pandas as pd
import numpy as np
import scipy as sp
from scipy import statsNumpyを使って配列型に数値を格納していきます!
data = np.array([205, 198, 197, 208, 204, 202, 207, 199, 207, 203])続いて、それらの配列型からサンプル数や不偏分散、標本平均を求めていきます。
n = len(data)
var = np.var(data, ddof=1) #不偏分散
mean = np.mean(data) #標本平均これらの値を元にtの値を求めていきます。
tの値は以下のように求めればよいのでした。
$$ t= \frac{\bar{x}-μ}{\sqrt{\frac{σ^2}{n}}} $$
ここにあてはめていくと以下のようになります。
(mean - 200)/(np.sqrt(var/n))
計算すると、2.4053511772118195となります。
これを自由度9(10-1)のt分布の有意水準5%の点と比較してみると・・・
2.405 > 1.833となり5%有意となりました!
ちなみにScipyを使って以下のように記述すれば簡単に同様の結果を得ることができます。
sp.stats.ttest_1samp(data, popmean=200)簡単ですね!
t検定をRで実装してみよう!

続いてRで実装してみましょう!
適当に10個のサンプルデータを入れて、それぞれの母平均の検定をt検定で行ってみました。
先程は1標本のt検定でしたが、こちらは2標本のt検定を行っています。
Two Sample t-test
data: x and y
t = -0.59024, df = 18, p-value = 0.5624
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-5.471301 3.071301
sample estimates:
mean of x mean of y
1.6 2.8
p-value = 0.5624>0.05なので5%有意にはなりませんでした。サンプル数が少なすぎましたね。
実際に簡単にt検定が行えることが分かっていただけたと思います。
t検定 まとめ
本記事では、t検定について見てきました。
t検定は様々な場面で使うことのできる有用な検定手法です。
カイ二乗検定とあわせて実務場面で活躍することが多いです。

検定は統計学の基本のキでありながら奥が深くしっかり理解しておく必要があります。
検定まわりのお話は以下の書籍がオススメです。是非目を通してみてください!
■入門 統計解析法
統計学の基本を理解するのにうってつけの本です。基本的に高校レベルの数学ができれば問題なく理解できるレベル。大学生1~2年生の時に非常にお世話になりました。
■統計学入門(基礎統計学)
東大出版から出ている名著です。
赤本と呼ばれ慣れ親しまれています。レベル的には中級者~上級者で、1冊持っておくと、なにかと便利な1冊です。
t検定を理解して実装してみて統計学の門をたたきましょう!
t検定以外にもいくつかの統計的検定があります。統計的検定については以下の記事で詳しくまとめていますので是非ご覧ください。

また統計学や少し発展した機械学習、そしてデータサイエンスやPythonの勉強について興味のある方は是非以下の記事をチェックしてみてください!




またこれらの知識を総合的に学べる「スタビジアカデミー(スタアカ)」というスクールを当メディアで運営しておりますので興味のある方は是非チェックしてみてください!
AIデータサイエンス特化スクール「スタアカ」

| 【価格】 | ライトプラン:1280円/月 プレミアムプラン:149,800円 |
|---|---|
| 【オススメ度】 | |
| 【サポート体制】 | |
| 【受講形式】 | オンライン形式 |
| 【学習範囲】 | データサイエンスを網羅的に学ぶ 実践的なビジネスフレームワークを学ぶ SQLとPythonを組みあわせて実データを使った様々なワークを行う マーケティングの実行プラン策定 マーケティングとデータ分析の掛け合わせで集客マネタイズ |
データサイエンティストとしての自分の経験をふまえてエッセンスを詰め込んだのがこちらのスタビジアカデミー、略して「スタアカ」!!
当メディアが運営するスクールです。
24時間以内の質問対応と現役データサイエンティストによる複数回のメンタリングを実施します!
カリキュラム自体は、他のスクールと比較して圧倒的に良い自信があるのでぜひ受講してみてください!
他のスクールのカリキュラムはPythonでの機械学習実装だけに焦点が当たっているものが多く、実務に即した内容になっていないものが多いです。
そんな課題感に対して、実務で使うことの多いSQLや機械学習のビジネス導入プロセスの理解などもあわせて学べるボリューム満点のコースになっています!
Pythonが初めての人でも学べるようなカリキュラムにしておりますので是非チェックしてみてください!
ウォルマートのデータを使って商品の予測分析をしたり、実務で使うことの多いGoogleプロダクトのBigQueryを使って投球分析をしたり、データサイエンティストに必要なビジネス・マーケティングの基礎を学んでマーケティングプランを作ってもらったり・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践してもらったりする盛りだくさんの内容になってます!
・BigQuery上でSQL、Google Colab上でPythonを使い野球の投球分析
・世界最大手小売企業のウォルマートの実データを用いた需要予測
・ビジネス・マーケティングの基礎を学んで実際の企業を題材にしたマーケティングプランの策定
・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践して稼ぐ
























