こんにちは！スタビジ編集部です！
今回は区間推定と95%信頼区間について解説をしていきます！
区間推定とは「抽出した一部のデータから、データ全体の特徴をある区間でもって推定する方法」のことです。
この記事では、区間推定とはどんなことをやっているのか？計算はどのように行うのか？について解説します！
・そもそも推定とは何かをイメージで理解！
・区間推定について解説！
・95%信頼区間とは何か？具体的な計算方法含め解説！
以下の動画でも解説していますのでチェックしてみてください！
そもそも推定とは！？
早速、区間推定や信頼区間について解説します！と、いきたいところですが。。
まず前提として、95%信頼区間や区間推定を学ぶ前に以下の点を抑えておきましょう！
推定とは？
推定とは、「本当は全データ分調べたいけどそれだと手間がかかり過ぎるので少ないデータで特徴を捉えよう！」というものです。
例えばクラス20人の平均身長なら求めることが可能かもしれませんが、アメリカ人男性の平均身長が知りたい..！となったときには全データで統計量を算出するのは厳しいですよね？
そこで登場するのが推定というわけです！
推定には、大きく分けて①点推定、②区間推定があります。
①点推定
「全データの中からサンプルを抜き出して、そのサンプルを元に平均値などの統計量を求め、推定値とする」
②区間推定
「取るサンプルの数にもよるが推定には誤差が生じることを考慮し、幅を持たせてあげて推定値とする」
それぞれの具体例は以下の通りです。
①の点推定ではピンポイントの値で推定するため区間という考え方は出てこないです。
一方で区間推定では、幅を持たせて推定を行うので95%信頼区間といった概念が出てくるんです！
②区間推定についてはもう少し詳しく考えていきましょう。
区間推定・95%信頼区間について解説！
調べたい全てのデータ（以降、母集団）があったときに、そこからランダムでサンプルを抜き出しますが、上手く真ん中の方からサンプルを抜き出してきているとは限りません。
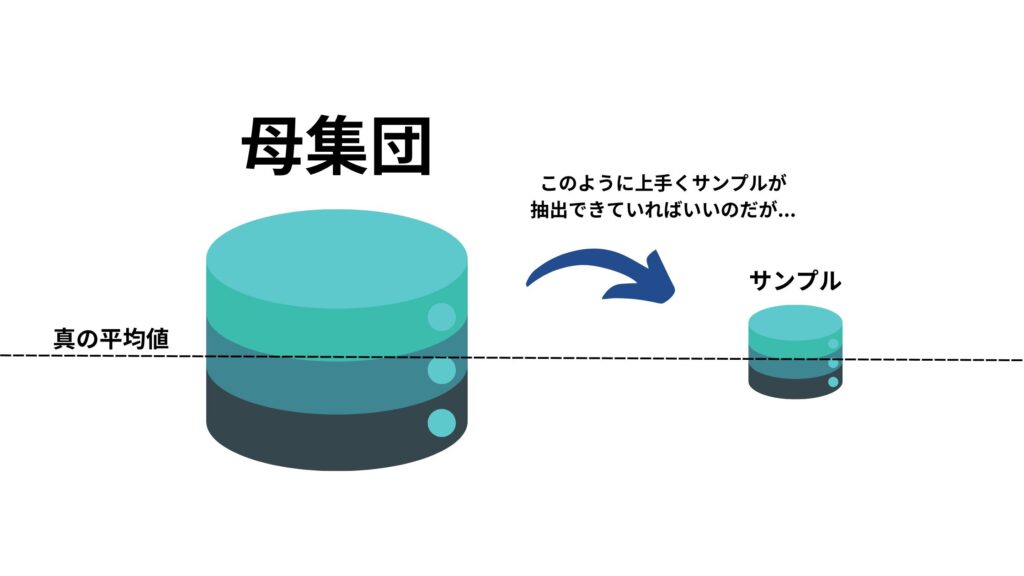
例えば平均値が知りたいとき、母集団のど真ん中から抜き出していれば推定値はぴったりです。
ですが実際にはランダムにサンプルを抜き出したとしても高めの層から抜き出してきてしまうケースもあれば、低めの層から抜き出してしまうケースもあるのです！
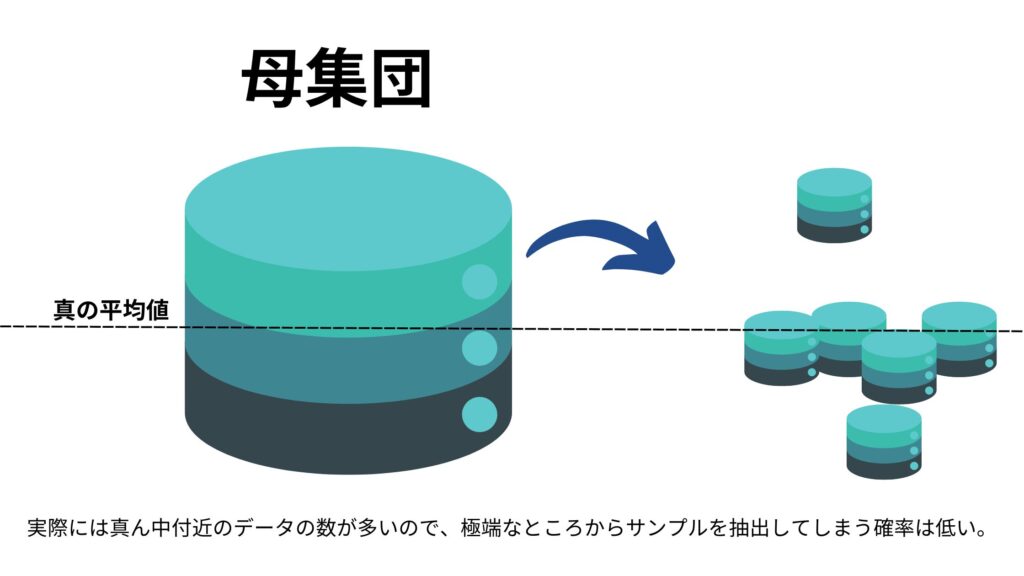
確率としては上記のようにすっごい高いところや低い所から抜き出してしまう可能性は低いし真ん中付近から抽出される可能性は高いでしょう。
これらを統計学的に計算し、「サンプル抽出した結果から信頼区間を求めた際に100回に95回くらいはその間に母平均が入るだろう！」を推定するのが区間推定であり、この区間が95%信頼区間なのです！！
95%信頼区間がもっとも一般的ですが、90%信頼区間や99%信頼区間などももちろん存在します。
95%信頼空間と比較すると90%信頼区間は狭くなり、99%信頼区間は広くなります！
具体的なイメージが以下になります。
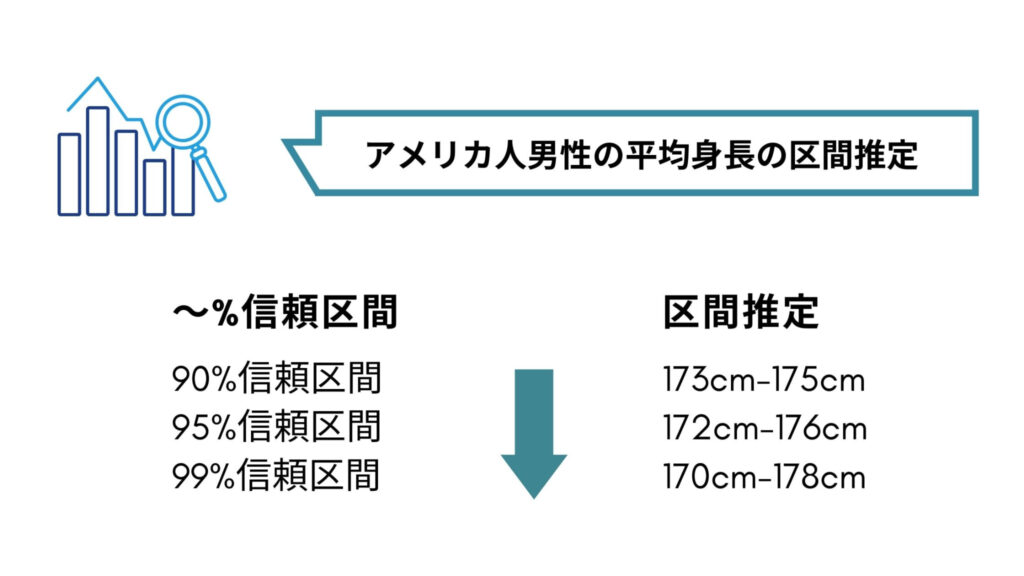
%が上がると、例えば99%信頼区間ではデータ抽出を繰り返すと100回に99回は全データの平均値が信頼区間の幅に収まっていなければならないと考えると区間が広くなっていくのが納得ですね！！
信頼区間の計算方法
ここから、実際に信頼区間を求めていきましょう。
少し数式が登場しますが、とりあえず概念だけ知りたい方は飛ばしてしまっても構いません！
ずばり結論から！
95%信頼区間は以下の式で計算されます！
\(\bar{x}-1.96\times\sqrt{\frac{\sigma^{2}}{n}}\leq\mu\leq\bar{x}+1.96\times\sqrt{\frac{\sigma^{2}}{n}}\)
それでは式に出てくる、\(\bar{x}\)・\(\sigma^{2}\)・\({n}\)について説明します！
\(\bar{x}\)は、抽出したサンプルの平均値を表します。100人の身長を測ったらその平均が174cmだった場合、これが\(\bar{x}\)に当たります。
気付いた方もいるかもしれませんが、これはそのまま点推定値になります！
続いて、\(\sigma^{2}\)。これは母分散に該当します。
データがどれくらいばらついているかを表す指標に他ならないですが、現実に推定する際には母分散も母平均同様分かっていないケースがほとんどです。
そんなときに標本から母集団の分散を推定する際、不偏分散が用いられます。
\(s^{2}\)などで表されますが\(\sigma^{2}\)のところを\(s^{2}\)に置き換えて推定する場合もあるんだ―とここでは知っていただければと思います。
この辺のTopicsについて詳しく知りたい方は以下の記事をご参照ください！！
最後に、\({n}\)。
これは簡単で、抽出したサンプルサイズ（→何個データを取ったか）のことを指します！
サンプルサイズ\({n}\)が大きくなると、\(1.96\times\sqrt{\frac{\sigma^{2}}{n}}\)の値が小さくなるので信頼区間の幅は狭くなりますね。
サンプルサイズが大きい方が、精度の高い推定となるのでイメージ通りではないでしょうか！
95%信頼区間の計算方法は以上となります！
ちなみに、90%信頼区間の場合の係数の値は1.96ではなく”1.64”、99%信頼区間の場合の係数の値は”2.58”になります。
t分布表というのを参照すると、これらの係数の値の対応が確認できます！
これらの係数と信頼区間を求める式からも、90%→99%などと%が上がると信頼区間の幅が広がることがわかります！
区間推定 まとめ
本記事では、区間推定のイメージについてや信頼区間の具体的な計算方法についてまとめました！
区間推定を理解し求められるようになることで、標本に対する考え方やデータへの理解が深まることに繋がっていきます！
また、今回推定を行う過程で平均値を例として示しましたが、それ以外にも推定されるものはたくさんあります！
異なる群の平均値の差の推定、オッズ比、回帰分析をした際の傾き（回帰係数）などがその例になります！
そして、不偏分散や自由度について（t分布含む）まとめたこちらの記事も見ていただけるとより理解が深まると思います！
このようなデータサイエンスの力を身に付けるためにはスタビジの記事やスクールを活用すると良いでしょう。
そして僕の経験を詰め込んだデータサイエンス特化のスクール「スタアカ（スタビジアカデミー）」を運営していますので，興味のある方はぜひチェックしてみてください！
AIデータサイエンス特化スクール「スタアカ」
| 【価格】 | ライトプラン：1280円/月 プレミアムプラン：149,800円 |
|---|---|
| 【オススメ度】 | |
| 【サポート体制】 | |
| 【受講形式】 | オンライン形式 |
| 【学習範囲】 | データサイエンスを網羅的に学ぶ 実践的なビジネスフレームワークを学ぶ SQLとPythonを組み合わせて実データを使った様々なワークを行う マーケティングの実行プラン策定 マーケティングとデータ分析の掛け合わせで集客マネタイズ |
データサイエンティストとしての自分の経験をふまえてエッセンスを詰め込んだのがこちらのスタビジアカデミー、略して「スタアカ」！！
当メディアが運営するスクールです。
24時間以内の質問対応と現役データサイエンティストによる複数回のメンタリングを実施します！
カリキュラム自体は、他のスクールと比較して圧倒的に良い自信があるのでぜひ受講してみてください！
他のスクールのカリキュラムはPythonでの機械学習実装だけに焦点が当たっているものが多く、実務に即した内容になっていないものが多いです。
そんな課題感に対して、実務で使うことの多いSQLや機械学習のビジネス導入プロセスの理解なども合わせて学べるボリューム満点のコースになっています！
Pythonが初めての人でも学べるようなカリキュラムしておりますので是非チェックしてみてください！
ウォルマートのデータを使って商品の予測分析をしたり、実務で使うことの多いGoogleプロダクトのBigQueryを使って投球分析をしたり、データサイエンティストに必要なビジネス・マーケティングの基礎を学んでマーケティングプランを作ってもらったり・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践してもらったりする盛りだくさんの内容になってます！
・BigQuery上でSQL、Google Colab上でPythonを使い野球の投球分析
・世界最大手小売企業のウォルマートの実データを用いた需要予測
・ビジネス・マーケティングの基礎を学んで実際の企業を題材にしたマーケティングプランの策定
・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践して稼ぐ
データサイエンスに関する記事はこちら！
データサイエンスを勉強できるスクールやサイトは、ぜひこちらを参考にしてみてください！
スタビジのコンテンツをさらに深堀りしたコンテンツが動画と一緒に学べるスクールです。
プレミアムプランでは私がマンツーマンで伴走させていただきます！ご受講お待ちしております！
