こんにちは！
データサイエンティストのウマたん（@statistics1012）です。
ある事象の仮説を数理的に確かめるために行われる統計的検定。
統計学の基本であり、様々なところで用いられている現場でも有用な手法です。
そんな統計的検定にはいくつか種類がありますが、この記事では実務で使われることの多いカイ二乗検定について見ていきたいと思います。
また検定全般に関して、以下の動画でも分かりやすく解説しています！
まずはじめにカイ二乗検定の理論を見ていき、最終的にはRで実装行っていきます！
カイ二乗検定とは？
カイ二乗検定は一見難しそうな検定なのですが、概念自体は非常に簡単。
具体的な例を挙げて見ていきましょう！
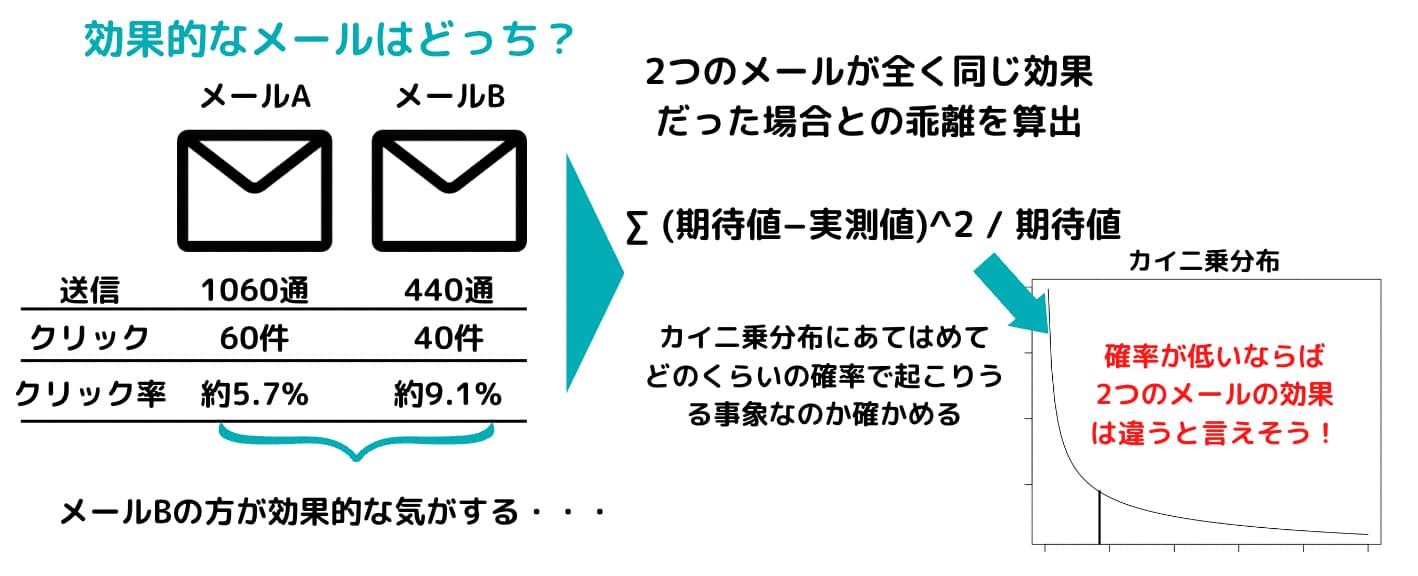
あるメールABの効果を確かめるためにランダムに振り分けたセグメントに配信を行いました。結果は以下の通り。
| クリックしなかった数 | クリックした数 | 配信数 | |
| メールA | 1000 | 60 | 1060 |
| メールB | 400 | 40 | 440 |
| 合計 | 1400 | 100 | 1500 |
※クリック数はメールからURLをクリックしてWebサイトへ遷移した数と定義します。
この時メールAとメールBでどちらの方が良いと言えるでしょうか？それとも、違いがあるとは言えないのでしょうか？
この時メールAとメールBでどちらの方が良いと言えるでしょうか？それとも、違いがあるとは言えないのでしょうか？
ここでカイ二乗検定の出番になります。
カイ二乗検定の計算方法
先ほどの例の場合、どのような計算を行ってカイ二乗検定の計算を行っていくのでしょうか？
簡単に見ていきます。そもそもABのメールに違いがなかったとしたらどうなるでしょう？
合計で1500通送ったうち100通がクリックされているわけですから、AもBも15分の1がクリックされることになるはず。
計算してみると・・・
Aは1060×(1/15)=70.7
Bは440×(1/15)=29.3
でも実際のところはAが60通で、Bが40通となっています。
これがたまたま誤差の範囲なのかそれとも決定的な違いがあるのかをカイ二乗検定により見ていくことになるわけです。
この差を以下の式で計算します。
$$ \sum\frac{(期待値-実測値)^2}{期待値} $$
すなわちこの場合は、クロス集計表の4セル全ての期待値を算出してそれぞれの実測値との値のズレの2乗を期待値で割ったものを全て足しあわせていきます。
$$ \frac{(70.7-60)^2}{70.7}+・・・ $$
結果は・・・5.88となりました。
この結果がカイ二乗値となり、カイ二乗値をもとにカイ二乗分布と照らしあわせてこの値が何％ほどで起こりうる値なのかを見てみます。
カイ二乗分布において自由度という指標が必要になるのですが、自由度は
$$ 自由度=(行数-1)×(列数-1) $$
で求めます。
今回は1になりますね！
自由度1でカイ二乗値が5.88の場合はどのくらいの確率で起きうるものなのでしょうか？
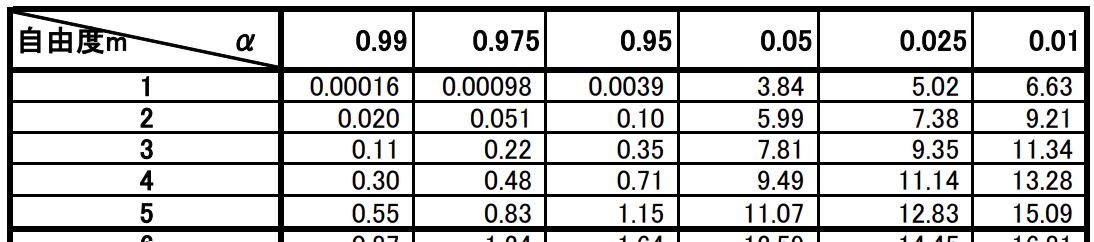
自由度1の時のカイ二乗分布の値は5％で3.84、1％で6.63、0.5％で7.88となっています。
通常は5％有意もしくは1％有意を用いますが、この場合5.88は3.84を上回っていますが6.63より小さいので5％有意となります。
つまりAとBが同じ前提の時、この事象は5%以下の確率でしか起きないということになるのです。
有意差については以下の記事をご参照ください。
カイ二乗検定の注意点
カイ二乗検定によって有意差があるかどうかと検定しましたが、検定においてはサンプルサイズの大きさが重要になってきます。
サンプルサイズが大きければ大きいほど少しの差で有意差を出しやすくなります。
例えば、先ほどの例でシンプルに全ての数値を約10％にシュリンクさせてみましょう！
| クリックしなかった数 | クリックした数 | 配信数 | |
| メールA | 100 | 6 | 106 |
| メールB | 40 | 4 | 44 |
| 合計 | 140 | 10 | 150 |
この場合、カイ二乗値を計算すると0.588になります。
先ほどの5%点が3.84であり、それを下回っているので有意差があるとは言えません。
同じ比率であるので直感的には有意差がありそうだと思えるかもしれませんが、サンプルサイズが小さい時は信頼性が低く有意差ありと判定されないのです。
あるLPに対して集客するユーザーは一定数なので、その中で何個もテストパターンを作ってしまうと、その分サンプルがばらけて十分なサンプルが得られるまで有意差ありと判定されにくくなってしまいます。
なので、ABテストなど行ってカイ二乗検定で有意差を判定したい時は、ABテストのパターンを細かくしすぎないほうがよいでしょう！
検定に値する十分なボリュームのサンプルが取得できるかをしっかり前もって設計しておきましょう！
カイ二乗検定をPythonで実装してみよう！
それでは続いてカイ二乗検定をPythonで実装してみましょう！
import pandas as pd
import numpy as np
import scipy as sp
from scipy import statsdata = pd.DataFrame([[1000, 60], [400, 40]])先ほどの例を使っていきたいので、このようにデータフレームを作成していきます。
続いて先ほど学んだようにそれぞれの期待値との差を以下のように計算していきカイ二乗値を算出していきます。
$$ \sum\frac{(期待値-実測値)^2}{期待値} $$
(60 - 1060/15)**2/(1060/15) + (1000 - 1060*14/15)**2/(1060*14/15) + (40 - 440/15)**2/(440/15) + (400 - 440*14/15)**2/(440*14/15)結果は、5.880911541288903となりました。
この値を自由値1のカイ二乗分布の有意水準5％の点と比較してみると・・・
5.88 > 3.84となり、5％有意となりました！
今回は実際に計算をして求めてきましたが、Scipyを使えば以下のように簡単に記述して同様の結果を得ることも可能です。
sp.stats.chi2_contingency(data, correction=False)簡単ですね！
カイ二乗検定 まとめ
カイ二乗検定についてまとめてきました。
カイ二乗検定は実務で活躍することの多い手法であり、簡単に実装できれば一目置かれること間違いなしです！
ちなみにカイ二乗検定を実際に行うWebアプリケーションをPythonで作る方法を以下の記事でまとめていますのでよければご覧ください！
検定は統計学の基本のキでありながら奥が深くしっかり理解しておく必要があります。
検定まわりのお話は以下の書籍がオススメです。是非目を通してみてください！
■入門 統計解析法
統計学の基本を理解するのにうってつけの本です。基本的に高校レベルの数学ができれば問題なく理解できるレベル。大学生１～２年生の時に非常にお世話になりました。
■統計学入門（基礎統計学）
東大出版から出ている名著です。
赤本と呼ばれ慣れ親しまれています。レベル的には中級者～上級者で、1冊持っておくと、なにかと便利な1冊です。
カイ二乗検定を理解して実装してみて統計学の門をたたきましょう！
カイ二乗検定以外にもいくつかの統計的検定があります。統計的検定については以下の記事で詳しくまとめていますので是非ご覧ください。
統計学、機械学習、データサイエンスについて詳しく学びたい方は以下の記事をチェックしてみてください！
またデータサイエンティストになるための勉強がしたい！という方は当サイト「スタビジ」が提供するスタビジアカデミーというサービスで体系的に学ぶことが可能ですので是非参考にしてみてください！
スタビジのコンテンツをさらに深堀りしたコンテンツが動画と一緒に学べるスクールです。
プレミアムプランでは私がマンツーマンで伴走させていただきます！ご受講お待ちしております！
