こんにちは！スタビジ編集部です！
統計学や機械学習を学んでいると、様々な距離に出会うと思います。
ユークリッド距離、マンハッタン距離、マハラノビス距離などなど、、、。
今回はいくつか存在する距離の中から、ユークリッド距離とマンハッタン距離に焦点を当てて解説していきます！
様々な分析手法で登場する距離なので、しっかりと押さえておきましょう！
ユークリッド距離(L2ノルム)とは
ユークリッド距離（L2ノルム）とは、2点間の距離計算に、ピタゴラスの定理の公式を適用した距離です。
ある2点間の最短距離を求める方法であるとも言えますね。
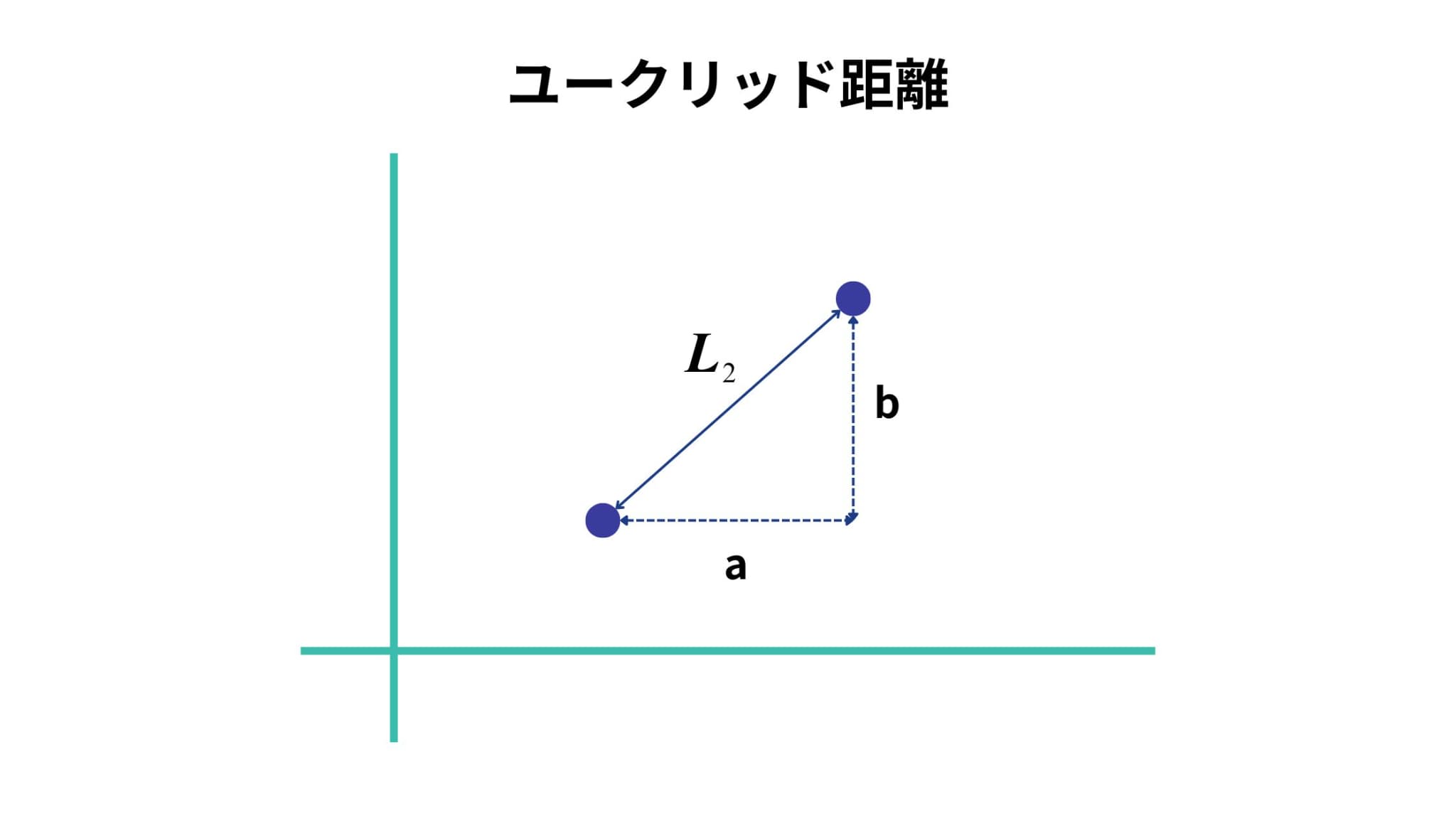
計算式は以下の通り（2次元の場合）。
\(\displaystyle L_{2} =\sqrt{a^2+b^2}\)
ちなみに多次元の場合も以下の式のようにピタゴラスの定理が成立します。
\(\displaystyle L_{2} =\sqrt{a^2+b^2+c^2+\cdots +n^2}\)
マンハッタン距離(L1ノルム)とは
マンハッタン距離（L1ノルム）とは、2点間の距離計算の際に、次元ごとの距離の絶対値を合計する方法です。
もう少しわかりやすく説明すると、碁盤の目のような道をタクシーが進む場合の縦と横の距離を合計するという方法です。
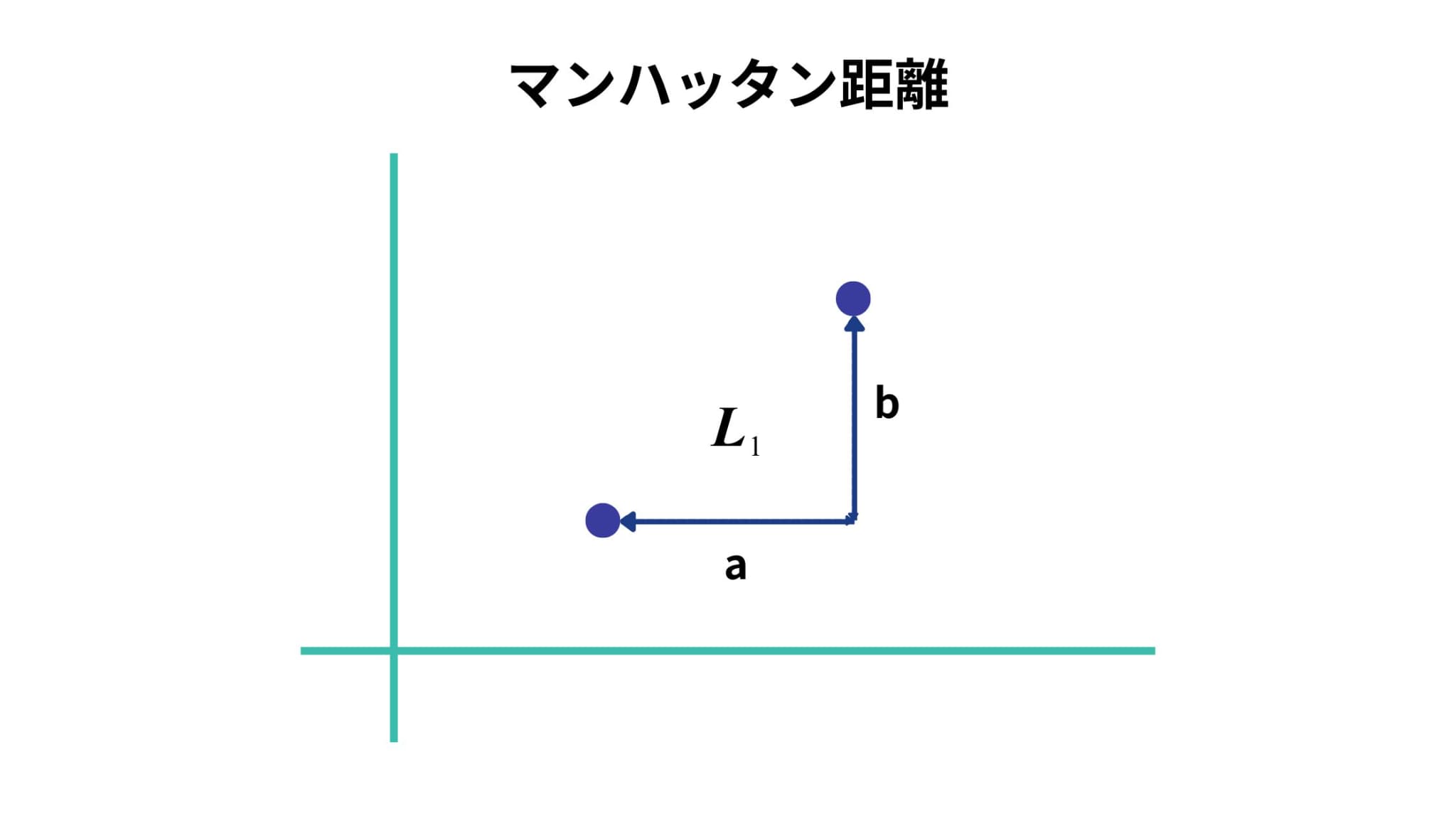
計算式は以下の通り（2次元の場合）。
\(\displaystyle L_{1} =\left| a \right|+\left| b \right|\)
多次元の場合は以下の式のように表すことができます。
\(\displaystyle L_{1} =\left| a \right|+\left| b \right|+\cdots +\left| n \right|\)
それぞれのメリット
ユークリッド距離とマンハッタン距離について説明しましたが、それぞれどんなメリットがあるのでしょうか。
ユークリッド距離のメリットは、最短距離を表現できることです。
その直感的理解のしやすさから、クラスタリングや異常検知など様々な分析手法に用いられています。
しかし、ユークリッド距離よりもマンハッタン距離を用いた方が良い場合もあります。
例えば、以下のようなアンケートデータを分析するとき。
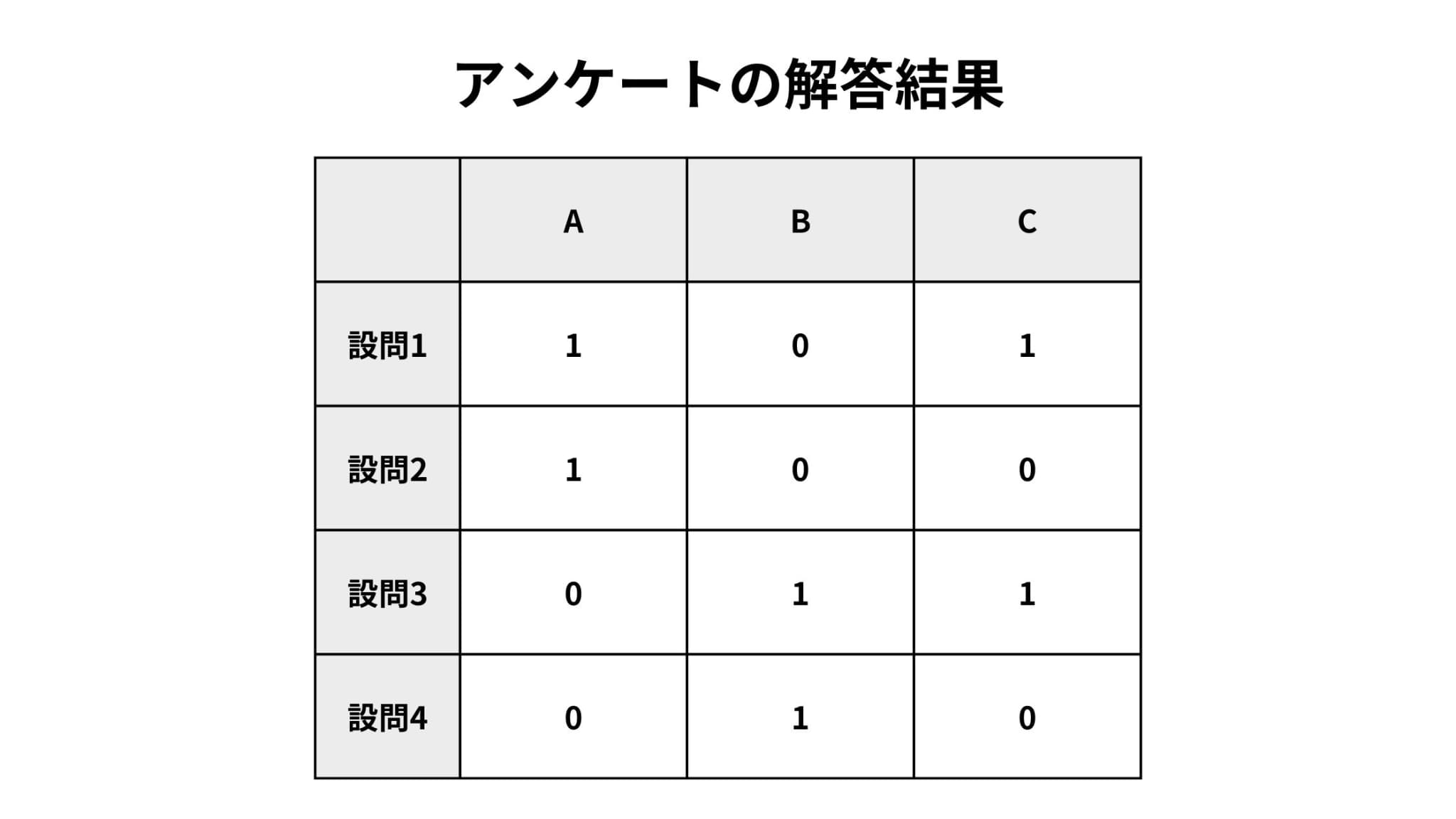
各人のユークリッド距離とマンハッタン距離を計算すると、以下のようになります。
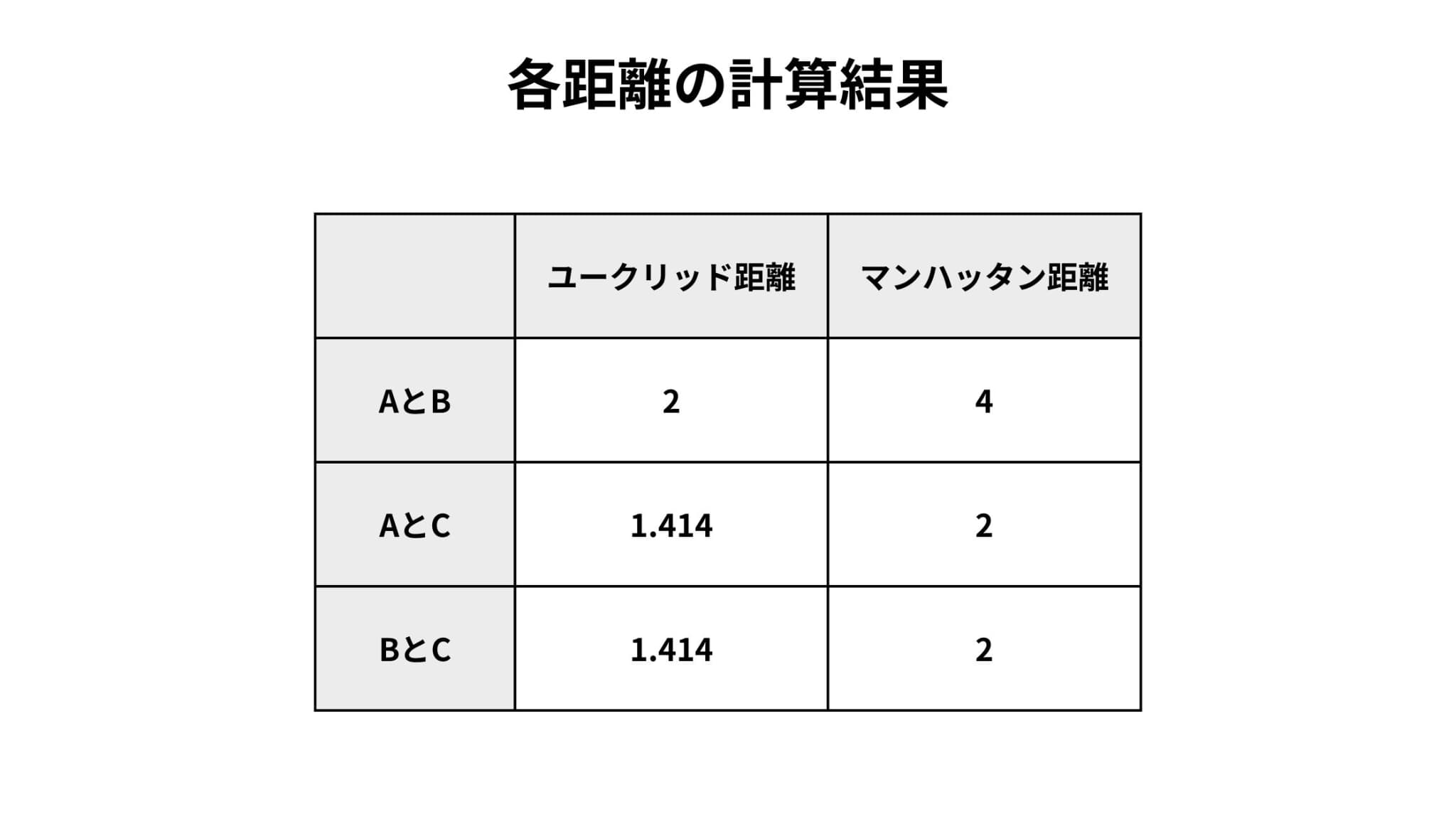
この場合、AさんとBさんの解答は100%異なり、AさんとCさんの解答は50%異なるため、AとBの距離とAとCの距離は2倍違うのが直感的なイメージですが、ユークリッド距離では2÷1.414=1.414倍しか違いがありません。
一方、マンハッタン距離では2倍の違いが現れており、直感に近い結果となっていることがわかります。
つまり、マンハッタン距離のメリットは、遠さ(違い)をより厳しく評価できるということです。
このような性質から、画像認識や自然言語処理などで用いられることがあります。
Pythonで計算してみよう
ここからは、Pythonで実際にユークリッド距離とマンハッタン距離を計算してみます。
次元数を変えてみて、それぞれどのような特徴があるかを見ていきましょう！
以下の流れで計算をしていきます。
1. ライブラリのインストール
2. データの準備
3. 距離の計算
1. ライブラリのインストール
今回は数値計算ライブラリであるNumpyを使用していきます。
#ライブラリのインストール
import numpy as np2. データの準備
2次元の場合と10次元の場合のデータをそれぞれ準備します。
np.arrayを用いて、それぞれのベクトルを配列として扱っていきます。
#データの準備
#2次元の場合
a = np.array([1,2])
b = np.array([5,6])
#10次元の場合
c = np.array([1,1,1,1,1,1,1,100,100,100])
d = np.array([1,1,1,1,1,1,1,1,1,1])3. 距離の計算
2点abの距離(2次元)と2点cdの距離(10次元)をそれぞれ計算していきましょう。
Numpyのnp.linalg.norm(配列A – 配列B)という関数を使用しています。
#距離の計算
#2次元の場合
#ユークリッド距離を計算
dist_Euclidean = np.linalg.norm(a - b)
print('abのユークリッド距離:',dist_Euclidean)
#マンハッタン距離を計算(ord=1を指定することで計算可能)
dist_Manhattan = np.linalg.norm(a - b, ord=1)
print('abのマンハッタン距離:',dist_Manhattan)
#10次元の場合
#ユークリッド距離を計算
dist_Euclidean = np.linalg.norm(c - d)
print('cdのユークリッド距離:',dist_Euclidean)
#マンハッタン距離を計算(ord=1を指定することで計算可能)
dist_Manhattan = np.linalg.norm(c - d, ord=1)
print('cdのマンハッタン距離:',dist_Manhattan)
ab間、cd間の両方でユークリッド距離の方が小さいことがわかります。
またcd間の距離に着目すると、ユークリッド距離とマンハッタン距離の違いはかなり大きく、マンハッタン距離の方が大きいことがわかります。
ベクトルc、dでは10次元の内3次元だけが異なるというデータであったため、マンハッタン距離の方が違いをより厳密に表現できていると言えます。
多少の違いは無視してもよい場合はユークリッド距離、多少の違いも検出したい場合はマンハッタン距離を用いるというような使い分けをしていきましょう！
まとめ
本記事では、ユークリッド距離(L2ノルム)とマンハッタン距離(L1ノルム)について解説しました！
これらの距離は、様々な手法で用いられています。
それぞれの距離のメリットを考慮して、適切な使い分けをしていきましょう！
また、今回分析に用いたPythonについて勉強したい方は以下の記事を参考にしてみてください！
さらに詳しくAIやデータサイエンスの勉強がしたい！という方は当サイト「スタビジ」が提供するスタビジアカデミーというサービスで体系的に学ぶことが可能ですので是非参考にしてみてください！
AIデータサイエンス特化スクール「スタアカ」
| 【価格】 | ライトプラン：1280円/月 プレミアムプラン：149,800円 |
|---|---|
| 【オススメ度】 | |
| 【サポート体制】 | |
| 【受講形式】 | オンライン形式 |
| 【学習範囲】 | データサイエンスを網羅的に学ぶ 実践的なビジネスフレームワークを学ぶ SQLとPythonを組み合わせて実データを使った様々なワークを行う マーケティングの実行プラン策定 マーケティングとデータ分析の掛け合わせで集客マネタイズ |
データサイエンティストとしての自分の経験をふまえてエッセンスを詰め込んだのがこちらのスタビジアカデミー、略して「スタアカ」！！
当メディアが運営するスクールです。
24時間以内の質問対応と現役データサイエンティストによる複数回のメンタリングを実施します！
カリキュラム自体は、他のスクールと比較して圧倒的に良い自信があるのでぜひ受講してみてください！
他のスクールのカリキュラムはPythonでの機械学習実装だけに焦点が当たっているものが多く、実務に即した内容になっていないものが多いです。
そんな課題感に対して、実務で使うことの多いSQLや機械学習のビジネス導入プロセスの理解なども合わせて学べるボリューム満点のコースになっています！
Pythonが初めての人でも学べるようなカリキュラムしておりますので是非チェックしてみてください！
ウォルマートのデータを使って商品の予測分析をしたり、実務で使うことの多いGoogleプロダクトのBigQueryを使って投球分析をしたり、データサイエンティストに必要なビジネス・マーケティングの基礎を学んでマーケティングプランを作ってもらったり・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践してもらったりする盛りだくさんの内容になってます！
・BigQuery上でSQL、Google Colab上でPythonを使い野球の投球分析
・世界最大手小売企業のウォルマートの実データを用いた需要予測
・ビジネス・マーケティングの基礎を学んで実際の企業を題材にしたマーケティングプランの策定
・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践して稼ぐ
スタビジのコンテンツをさらに深堀りしたコンテンツが動画と一緒に学べるスクールです。
プレミアムプランでは私がマンツーマンで伴走させていただきます！ご受講お待ちしております！
