先日、MEWMA管理図についてご紹介しました！
ホテリング管理図に対して、微小な変化を検知できるMEWMA管理図！
実務ベースでの実用が期待されます。
しかし、MEWMA管理図が検知できるのは平均ベクトルの変化のみ。
分散共分散行列の変化など多彩な変化を検知することはできません。
そこで登場したのが
MEWMC管理図！
MEWMC管理図とは
MEWMC管理図は(Multivariate Exponentially Weighted Moving Covariance matrix)の略で、分散共分散行列の変化を可能にした手法です！
ミネソタ大学のMaboudou-Tchao氏が2008年に提案した比較的新しい手法です！
非常に有用な手法で、新しいブレークスルーを起こしました。
日本での文献はほとんど見当たらず、ネットで調べても全く出てこないのでこちらでご紹介します！
平均の変化は検知できるMEWMA管理図も分散が変化する状況においては対応できません。
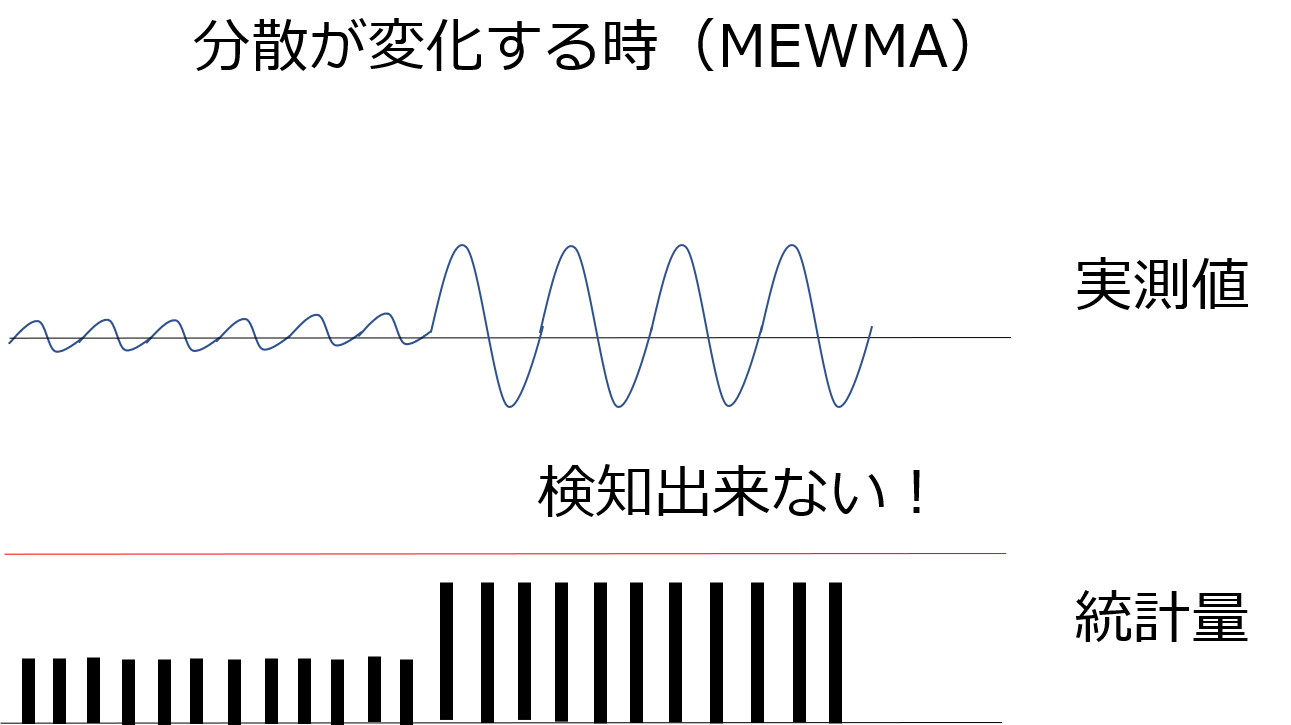
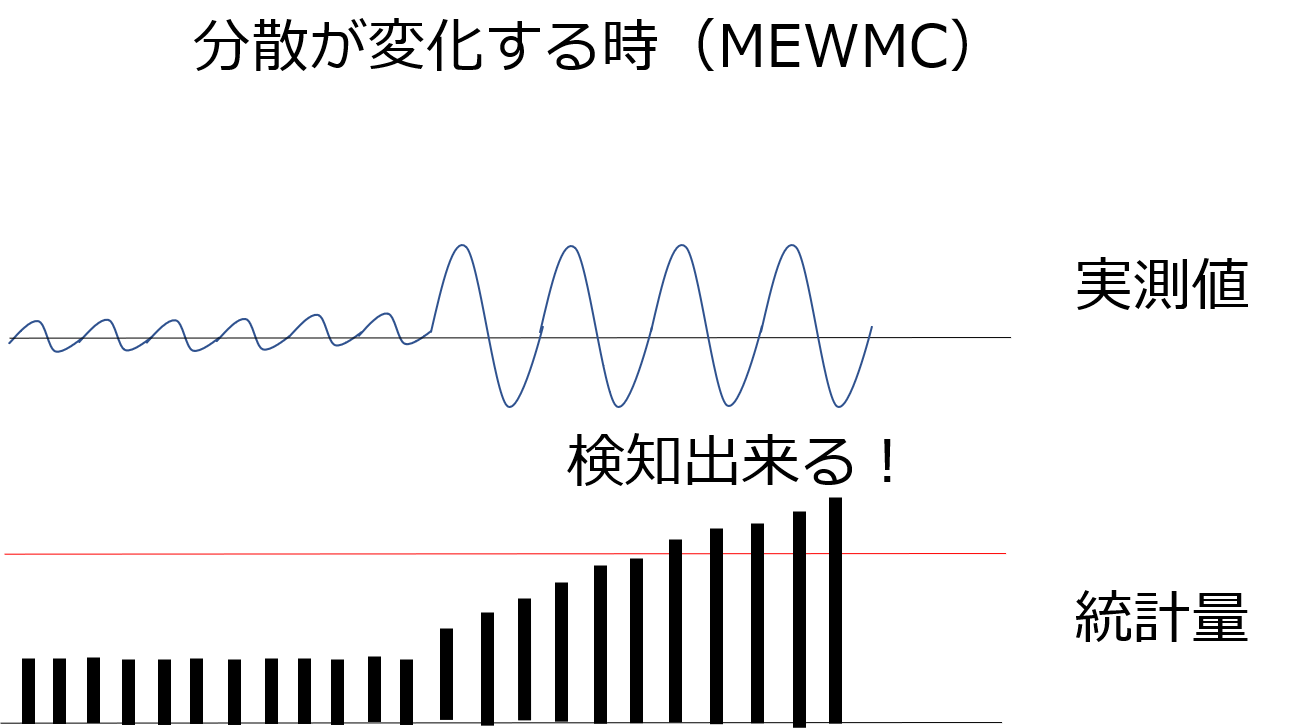
MEWMC管理図ではこのような分散の変化も検知することができます！
MEWMC管理図のアルゴリズム
それでは具体的にMEWMC管理図のアルゴリズムを見ていきましょう！以下のような多変量正規分布に従ってデータが発生しているとします！
\begin{eqnarray}
\left\{
\begin{array}{l}
x_t\sim{N_p(\mu_0,\Sigma_0)}(t=1,2,….,\tau)\\
x_t\sim{N_p(\mu_t,\Sigma_t)}(t=\tau+1,\tau+2….)\\
\end{array}
\right.
\end{eqnarray}
STEP1：多変量正規分布に従うデータが得られたとき、そのデータを白色化(多変量における標準化)します
\(A\Sigma_0A’=I_p\)を満たす\(A\)を用いて\(U_t=A(x_t-\mu_0)\)として白色化を行う
STEP2：得られた白色化ベクトルの要素を掛け合わせることで疑似分散共分散行列を算出し、各期ごとに蓄積する。
\begin{eqnarray}
S_t=(1-\lambda)S_{t-1}+\lambda{U_t}U_t’
\end{eqnarray}
この時\(S_0=I_p\)とする。
STEP3：最終的に得られた\(S_t\)を対数尤度に代入しMEWMC統計量とします。
\begin{eqnarray}
MEWMC_t=tr(S_t)-log(S_t)-p
\end{eqnarray}
MEWMC管理図を用いて、様々な変化を検知しましょう！
MEWMC管理図 まとめ
MEWMC管理図についてまとめてきました。なかなかマイナーな多変量管理図手法ですが、管理図の歴史の中では相当新しい手法です。
以下の記事で他の管理図についてまとまているので良ければご覧ください！
スタビジのコンテンツをさらに深堀りしたコンテンツが動画と一緒に学べるスクールです。
プレミアムプランでは私がマンツーマンで伴走させていただきます！ご受講お待ちしております！
