多変量管理図においてマハラノビス距離を用いて異常検知を行うホテリング管理図は大きな変化は素早く検知することができますが、小さい変化は簡単に検知することができません。
それに対して、MEWMA（Multivariate Exponential Weighted Moving Average：多変量指数重み付け平均変化）管理図という手法が存在します。長い名前ですね！笑
Lowryという人が1992年に提案して、今では多変量管理図のスタンダードになっています。
基本的には単変量におけるEWMA管理図を多変量に拡張したものになりますが、分散共分散行列についても重み付けを行うので若干プラスアルファの知識が必要です！
それでは、まずEWMA管理図の知識のおさらいから入りましょう！
EWMA管理図に関する記事はこちら→EWMA管理図
EWMA管理図
MEWMA管理図では過去のデータと今のデータに対してパラメータを用いて重み付けをします。ホテリング管理図では今のデータしか用いないため小さいデータを蓄積していくことができません。
以下の図は単変量の時の概念図です！
見ていきましょう！！
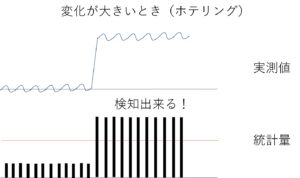
変化が大きい時、ホテリング管理図でも検知できますね！
しかし変化が小さいとどうでしょう？
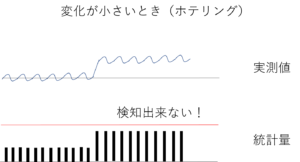
ホテリング管理図ではその期の評価しか行わないため小さい異常だと検知できないのです！！
そこでMEWMA管理図（単変量の場合はEWMA管理図）が考案されました！
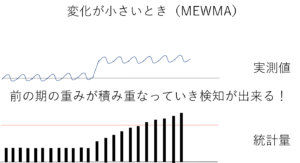
徐々に前の期の重み付け情報が積み重なっていき、最終的に異常検知ができるのです！！
MEWMA管理図の数理的アルゴリズム
さて具体的に数理的なアルゴリズムを見てみましょう！
具体的な手法は以下のようになります。
以下のような多変量正規分布を想定します。
$${\bf x_t}\sim{N_p}({\bf \mu_0}, {\bf \Sigma_0}), (t=1,2,…,\tau)$$
$${\bf x_t}\sim{N_p}({\bf \mu_t}, {\bf \Sigma_t}), (t=\tau+1,\tau+2,…)$$
この時\(lambda\)に基づいて指数的な重みづけを行います。
$${\bf w_t}=(1-\lambda){\bf w_{t-1}}+\lambda(\bf x_t-\bf \mu_0), \bf w_0=0$$
この統計量と重み付けした分散共分散行列の逆行列を掛け合わせ、ホテリング管理図と同じ要領で最終的に判定に用いる統計量を算出します。
$$MEWMA_t={w_t}^{T}{\Sigma_{w_t}}^{-1}{w_t}$$
この時、重み付けした分散共分散行列は以下のように定義されます。
これに関する導出はLowryの論文にも詳しく載っていませんが、単変量で考えて重み付けした変量の分散がｔ→∞期でどのようになるか計算してみるとそれっぽい式がでてきます。
$$\Sigma_{w_t}=\frac{\lambda}{2-\lambda}\Sigma_0$$
MEWMA管理図の評価指標
評価指標にはARL(Average Run Length：平均連長)を用います。
これは管理限界線を越えるまでどのくらいのサンプルが続いたかを示す指標となります。
単変量では標本平均と標本分散などから理論的に閾値を決められたのですが、MEWMAでは理論的に決めることができません。モンテカルロシミュレーションで求めます。
正常状態のARLをIC-ARL(In control ARL)と呼びこれは大きければ大きいほど良いです。異常状態のARLをOC-ARL(Out of control ARL)と呼びこれは小さければ小さいほど良いです。
基本的にはIC-ARLをいくつかに固定したうえで、OC-ARLの小ささを評価します。IC-ARLは200,370などが多いようですが、私は専ら200でやっています。
MEWMA管理図 まとめ
いかがだったでしょうか。概念的には非常に簡単で全く難しくありませんが、なかなか文献がなくて困ります。大体英語の文献になっちゃいます。ここらへんの多変量管理図について興味のある人はまず、Lowry(1992)の論文を見てみるとよいと思います！
ちなみにMEWMA管理図は平均の変化だけに対応した手法です。
分散の変化や、平均と分散の同時変化に関してはこちらのページをご覧ください！
分散の変化→MEWMC管理図
平均と分散の同時変化→ELR管理図
以下の記事で他の管理図についてまとまているので良ければご覧ください！
スタビジのコンテンツをさらに深堀りしたコンテンツが動画と一緒に学べるスクールです。
プレミアムプランでは私がマンツーマンで伴走させていただきます！ご受講お待ちしております！
