【手計算で紹介】パーセプトロンを簡単な例でわかりやすく解説!

こんにちは!
外資系でのデータサイエンティストを経て現在は会社経営をやっているウマたん(@statistics1012)です!
この記事ではディープラーニングやニューラルネットワークの基本となる「パーセプトロン」について見ていきたいと思います。
パーセプトロンについては以下の書籍「ゼロから作るディープラーニング」について詳しく載っています。
この記事では、この書籍を参考にしながら解説していきたいと思います。
パーセプトロンを理解しておくだけで、ニューラルネットワーク・ディープラーニングの理解がビックリするくらい進むので是非この記事で理解を深めてください!
動画でも解説しているので以下もあわせてチェックしてみてください!
パーセプトロンの仕組み
パーセプトロンとは、ローゼンブラットという研究者によって1957年に考案されたアルゴリズムです。
非常に古くからある、このパーセプトロンですが、ニューラルネットワークそして多層ニューラルネットワークであるディープラーニングにつながる大事なアルゴリズムなのです。
パーセプトロンとはある信号を入力として受け取り、あるルールに基づいて変換し、特定の信号を出力するものです。
パーセプトロンの考え方は、人間の神経回路が信号を伝達していく流れをシンプルにしたものなんです。
このパーセプトロンでは、信号を流す(1)か流さない(0)かの2値の値で表現します。
ある入力信号x1,x2に対して重みを付けて足し合わせたものを出力yとします。
重みは適当にw1,w2と付けておきましょう!
こんな形の絵でイメージしてください。
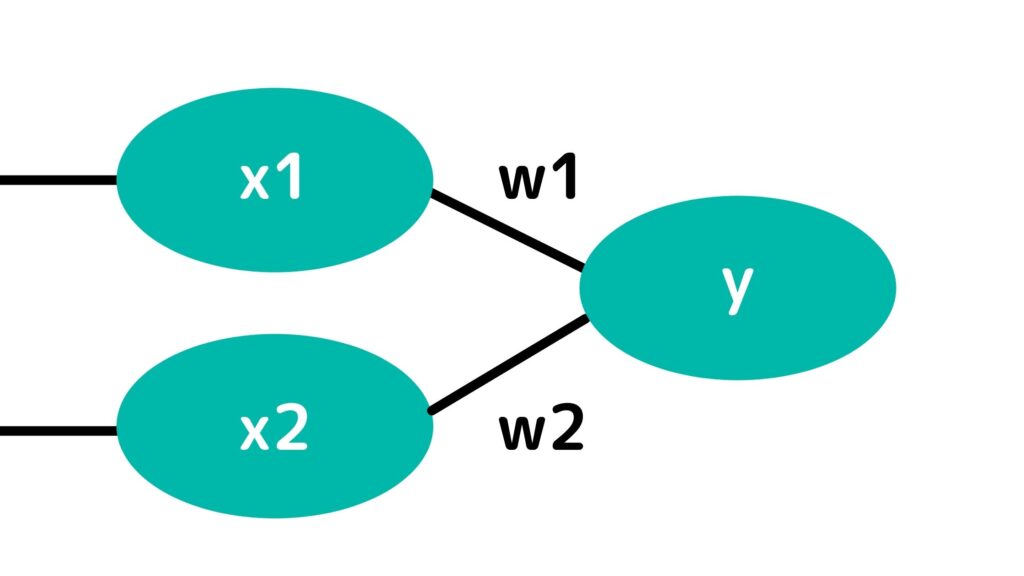
この時yは決められた閾値に応じて反応します。
特定の閾値θを超えた場合1を出力し、超えなかった場合は0を出力します。
これを式で表すと以下のようになります。
\begin{eqnarray} y= \left\{ \begin{array}{l} 0~~(w_1x_1+w_2x_2<=\theta) \\ 1 ~~ (w_1x_1+w_2x_2>\theta) \end{array} \right.\end{eqnarray}
こんな形でパーセプトロンを定義します。
この時、x1、x2は信号を流すか流さないかの1もしくは0になるのでした。
その際に以下のようにx1とx2の組み合わせに対してyを出力したいとしましょう。
こんな組み合わせです。
| x1 | x2 | y |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
x1,x2のどちらかが0であれば0を出力し、どちらも1であれば1を出力するというものです。
この時(w1,w2,θ)の組み合わせには何があるか考えてみましょう!
このようになる(w1,w2,θ)の組み合わせは実はたくさん考えられるのですが、例えば(0.4,0.4, 0.5)などが1つの例になります。
これを先程の式に当てはめてみると、、、このようになり、
\begin{eqnarray} y= \left\{ \begin{array}{l} 0~~(0.4x_1+0.4x_2<=0.5) \\ 1~~ (0.4x_1+0.4x_2>0.5) \end{array} \right.\end{eqnarray}
ちゃんと、
$$ 0.4×0+0.4×0=0<=0.5~~y=0 $$
$$ 0.4×1+0.4×0=0.4<=0.5~~y=0$$
$$ 0.4×0+0.4×1=0.4<=0.5~~y=0$$
$$ 0.4×1+0.4×1=0.8>0.5~~y=1$$
と表のようになってますね!
続いて以下のようにx1とx2の組み合わせに対してyを出力したいとしましょう。
| x1 | x2 | y |
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
こちらは先の組み合わせとは完全に逆のパターンであり、今度は1つでも0が入力にあれば出力は1になって、入力がどっちも1であれば出力は0になります。
この時も同様にパラメータ(w1,w2,θ)を変えれば実現することが出来ます。
先ほどの逆なので先ほどのパラメータを反転させて(0.4,0.4, 0.5)などのようにすれば実現することができます。
\begin{eqnarray} y= \left\{ \begin{array}{l} 1~~(0.4x_1+0.4x_2<=0.5) \\ 0~~ (0.4x_1+0.4x_2>0.5) \end{array} \right.\end{eqnarray}
これは問題なさそうですね。
さらに以下のような組み合わせも問題なくパラメータをいじることで実現することができるのが分かるでしょう。
| x1 | x2 | y |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
今回は、1つでも入力に1があれば出力が1になって、どっちも入力が0の時だけ出力が0になってますね!
例えば、(w1,w2,θ)に(1,1,0.5)を入れれば実現できますね
\begin{eqnarray} y= \left\{ \begin{array}{l} 0~~(x_1+x_2<=0.5) \\ 1~~ (x_1+x_2>0.5) \end{array} \right.\end{eqnarray}
$$ 1×0+1×0=0<=0.5~~y=0 $$
$$ 1×1+1×0=1>0.5~~y=1$$
$$ 1×0+1×1=1>0.5~~y=1$$
$$ 1×1+1×1=2>0.5~~y=1$$
ちゃんと組み合わせを実現できていることが分かりました!
このように特定の入力に対して特定の出力がされるように人間の手でパラメータをいじってルールを作ることができました。
今回は人間が手動で行いましたが、これを機械が調整してくれるのが機械学習であり、ニューラルネットワーク→ディープラーニングにつながっていきます。
このパーセプトロンの考え方は非常に重要であり、ディープラーニングを学ぶ上で重要な基礎となるポイントなので必ずおさえておきましょう!
パーセプトロンはどんな組み合わせでも表現できる?

さて、ここで1つの疑問がわきます。
どんな組み合わせでもパラメータをうまく調整すれば表現できるようになるのでしょうか?
例えば以下のような組み合わせはどうでしょう?
| x1 | x2 | y |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
どうやったら実現できるか考えてみましょう。
いかがでしょうか?
実はこの組み合わせは、これまでのパーセプトロンでは表現することができないのです。
なぜ実現できないのか考えてみましょう。
先ほどの以下の組み合わせは(w1,w2,θ)の(1,1,0.5)を入れた場合に実現できるのでした。
| x1 | x2 | y |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
式は以下のようになります。
\begin{eqnarray} y= \left\{ \begin{array}{l} 0 ~~ (x_1+x_2<=0.5) \\ 1 ~~ (x_1+x_2>0.5) \end{array} \right.\end{eqnarray}
この状態がどんな状態なのか図で見てみましょう。
x2とx1で軸を取って平面を展開した時に
\begin{eqnarray}x_2 = -x_1+0.5\end{eqnarray}
の関数を境界に1か0が分かれているので以下のようになるということが分かると思います。
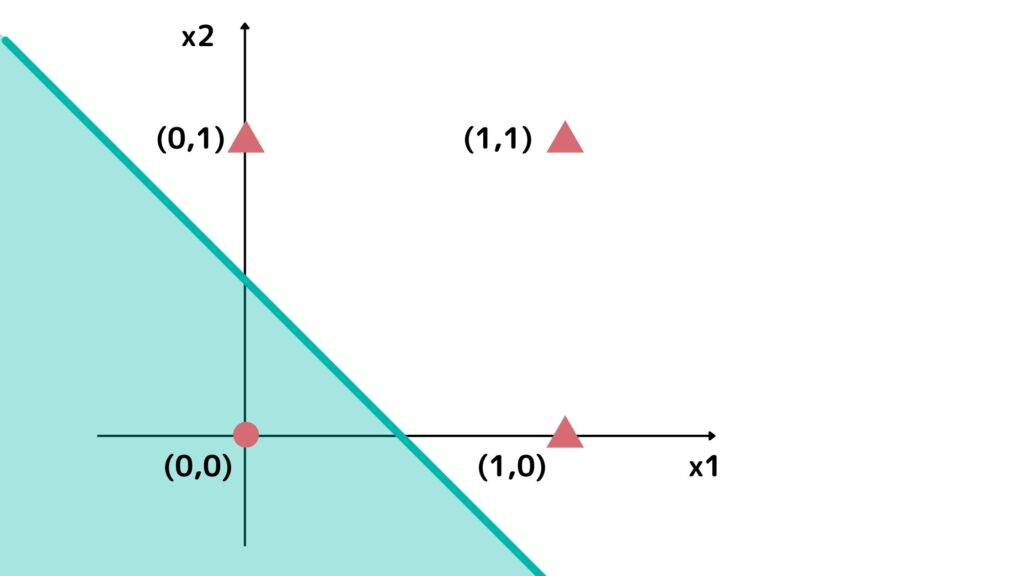
そして以下の表の組み合わせをy=0を◯、y=1を△にしてプロットしてみると・・・
| x1 | x2 | y |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
ちゃんと直線で分離することが出来ているのが分かると思います!
この境界範囲ならパラメータを動かしても問題ないでしょう。
しかし、先ほど考えてみた以下の組み合わせはいかがでしょうか?
| x1 | x2 | y |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
x1x2を軸に取ってプロットしてみると以下のようになります。
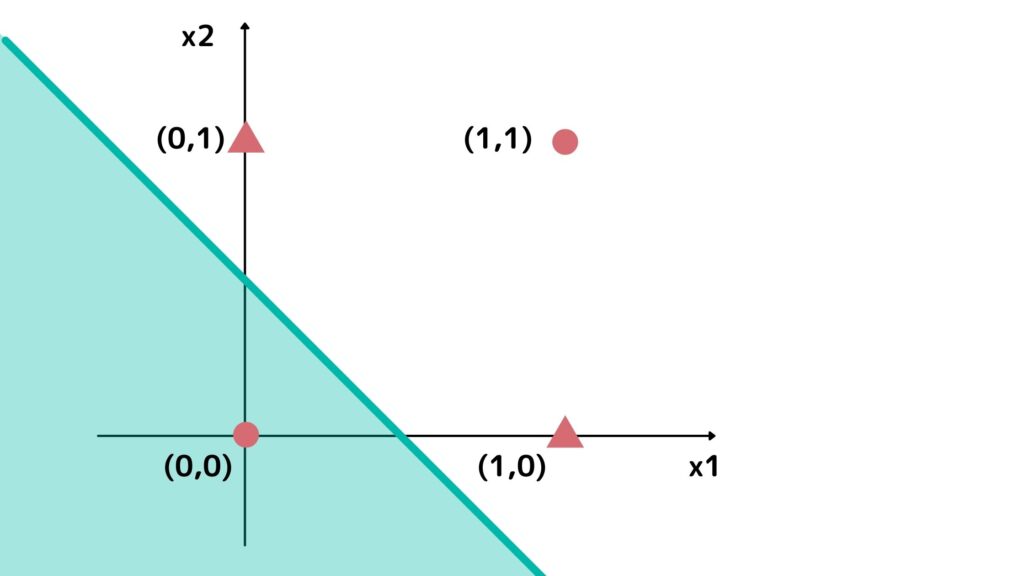
実はこれは直線では分けることができないのです。
どう頑張っても、座標(1,1)の◯を直線で捉えにいこうとすると△を内包してしまうことが分かると思います・・
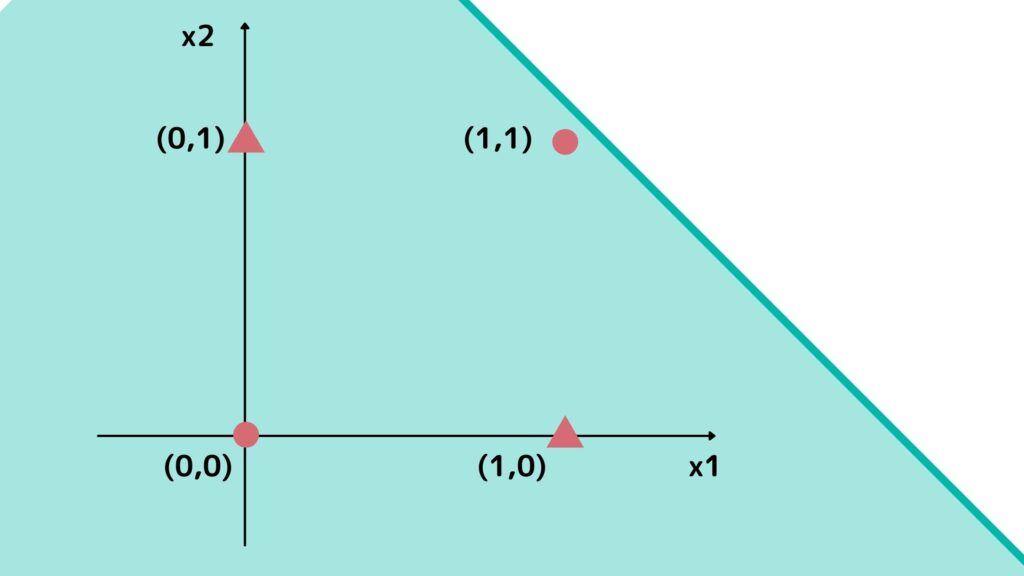
直線で判別することを線形判別と言いますが、これは線形判別ではうまく分けることができない組み合わせなのです。
しかし、このような組み合わせは現実問題には多く発生します。
複数のパーセプトロンを重ねる
ではどのようにすればこのような組み合わせを判別できるのでしょうか?
実はここでパーセプトロンを重ねるという発想が登場します。
なんと、単一のパーセプトロンでは上手く表現できないものも複数のパーセプトロンを使うことで表現することができるのです。
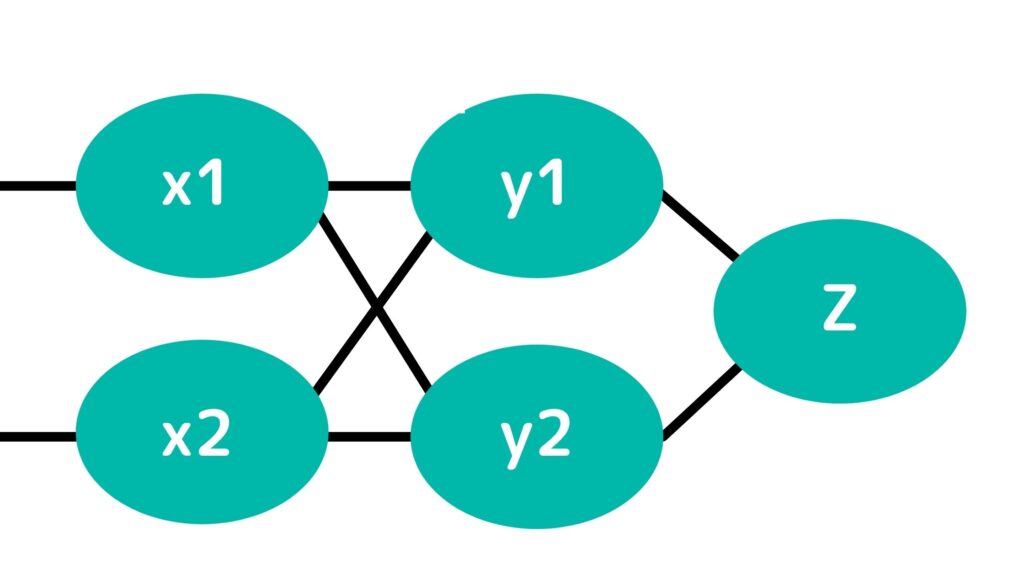
以下の組み合わせによるアウトプットのさらなる組み合わせによって実現されるのです。
| x1 | x2 | y1 | y2 | z |
| 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 |
x1とx2の組み合わせから生まれたy1とy2からzが生まれています。
分解すると、
| x1 | x2 | y1 |
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
| x1 | x2 | y2 |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
は今まで見てきた組み合わせであり、
| y1 | y2 | z |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
yを入力としてzを出力する、このパターンも1つでも0が入力であったら出力が0になる以下の組み合わせと同じであることが分かると思います。
| x1 | x2 | y |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
これら1つ1つを切り取ってみると実は今まで登場した組み合わせと一緒なのですが、複数組み合わせることでより複雑な分類問題に対応できるようになるのです!
これにより単一のパーセプトロンで実現できないことが実現できました。
これからニューラルネットワークやディープラーニングの世界に入っていきますが、このパーセプトロンの考え方が土台になっており非常に重要なので、必ずおさえておきましょう!
パーセプトロン まとめ
ここまででパーセプトロンについて簡単に分かりやすく解説してきました!
ここからニューラルネットワークやディープラーニングの世界に入っていきます。
ディープラーニングについては以下の書籍が非常に分かりやすくオススメなので是非チェックしてみてください!
パーセプトロンから更に踏み込んでニューラルネットワークやディープラーニングの実装についてはスタビジアカデミー(スタアカ)でまとめているので興味のある方は見てみてください!

また以下の記事でディープラーニングの勉強方法やディープラーニングが学べるスクールについてまとめていますのであわせて見てみてください!