層別解析について分かりやすく解説!Pythonで実装してみよう!

こんにちは!データサイエンティストのウマたん(@statistics1012)です。
統計的因果推論とは変数間の因果関係をデータから明らかにしようという分野で、ビジネスシーンでよく登場します。
そんな統計的因果推論の世界で、おさえておきたいのが層別解析というアプローチ。
この記事で学んで、しっかり理解しておきましょう!
ちなみに、統計的因果推論について詳しく知りたい方は以下の私のUdemy講座で学べますのでチェックしてみてください!
【初心者向け】統計的因果推論を学びPythonで実装していこう!RCT・層別解析・マッチング法・傾向スコアを学ぼう!
| 【時間】 | 3.5時間 |
|---|---|
| 【レベル】 | 初級 |
統計的因果推論について詳しく知りたいならこのコース!
今なら購入時に「J56MYR9S」という講師クーポンコードを入れると90%オフ以上の割引価格になりますのでぜひご受講ください!
以下のYouTube動画でも解説していますので合わせてチェックしてみてください!
相関関係と因果関係
さて、まずは相関関係と因果関係の違いについて見ていきましょう!
例えば、「年収と一日の平均摂取カロリーには負の相関関係がある」
と聞いたらみなさんはどのように思いますか?
「よっしゃ!年収をあげるためにカロリーを抑えよう!」と思うでしょうか?
でも実際にはカロリーを低く抑えることによって年収が上がるということは期待されません。
なぜなら相関関係があったとしても因果関係があるとは限らないからです。
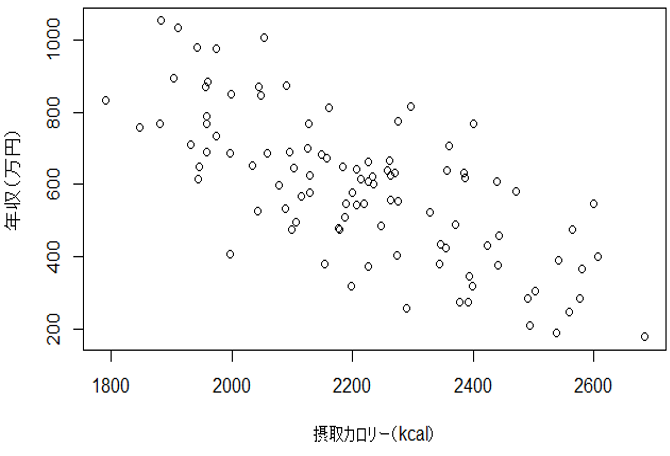
さて、先ほどの「年収と一日の摂取カロリー」には相関関係があることは間違いないです。
しかし、経験的に一日の摂取カロリーを低くしても年収が上がるという因果関係は認められないと思います。
それではなぜ「年収」を「摂取カロリー」の間に相関関係が見られたのでしょうか?
それは、「年収」と「摂取カロリー」の裏に「年齢」という隠れた因子が存在するからです。
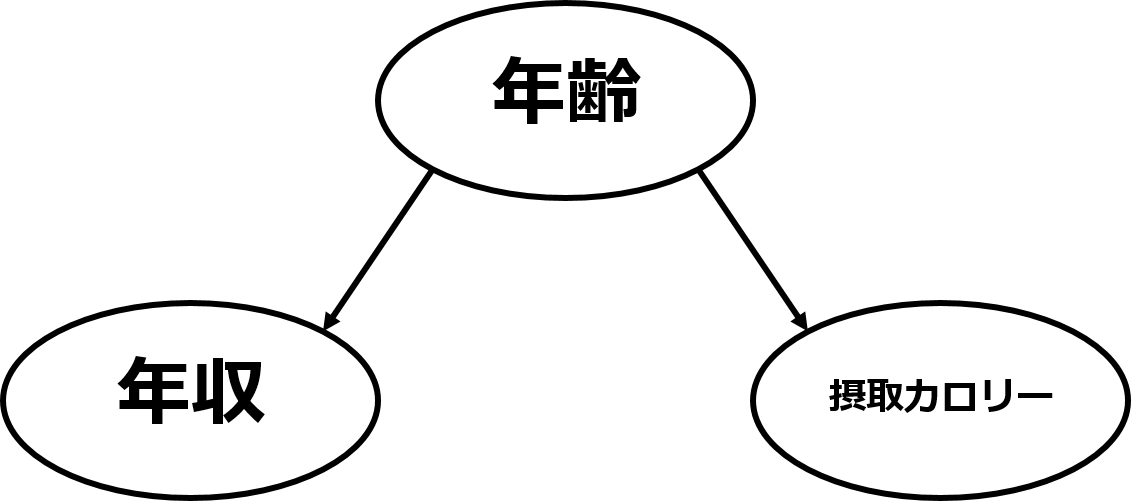
一般的に年齢が高くなると年収は上がります。そして年齢が高くなると摂取カロリーは低くなるでしょう。
そのため摂取カロリーが低い人ほど年収が高くなったのです。
このような変数間の構造のことを交絡と呼びます。
また、交絡しているときの相関を擬似相関(偽相関)と呼びます。
大事なのは相関関係があっても因果関係があるとは限らないということです。

層別解析が必要な場面
相関と因果の違いが分かったところで、層別解析が必要な場面について見ていきましょう!
ランダム化比較実験というアプローチができれば、それに越したことはないのですがそうでない場合は、様々なアプローチを考えなくてはならず、そのうちの1つが層別解析なのです。
どういうことか見ていきましょう!
例えば、ある新薬を飲んでもらう群と通常のビタミン剤を飲んでもらう群に分けて新薬の効果を見る実験をするとします。
この時、ある集団を新薬を飲んでもらう群(実験群・介入群・処置群などと呼ぶ)とビタミン剤を飲んでもらう群(対照群・統制群・コントロール群などと呼ぶ)に分けて、結果の差を見ます。
集団の中のそれぞれの対象が介入群と対照群のどちらになるかを決定させることを割り付けと呼びます。
では、集団をどのように割り付ければ良いでしょうか。
例えば、男性なら新薬を飲んでもらい、女性ならビタミン剤を飲んでもらうという割り付けをしてみます。
すると、確かに結果の差を得ることは出来ますが、果たしてそれは新薬の効果によるものなのでしょうか。性別に由来する影響かもしれません。
この場合、性別のことを交絡因子と呼びます。
このように割り付けを適切に行わないと交絡を引き起こしてしまいます。
結局、如何にして交絡に対処するかが重要ということです。
因果効果を測定するには交絡因子を調整する必要があります。
ここで登場する最も最適な方法が、割り付けを完全にランダムに行う方法でありランダム化比較実験(Randomized Controlled Trial;RCT)と呼ばれるのです。
RCTでは例えば、一人一人にコインを投げてもらい表なら介入群、裏なら対照群とします。
これによって、いろんな潜在的な交絡因子があっても二つの群の分布は平均的に等しくなることが期待されます。
RCTに関して詳しくは以下の記事をチェックしてみてください。

このRCTが実行できればよいのですが、そうとは限らないのが現実世界。
例えば、タバコと肺がんの関係を調べるために、ランダムに割り付けた人々に一日10本のタバコを吸ってもらい肺がんになるまで実験するというのは倫理的に不可能です。
また、コストの問題もありますし、そもそもすでにデータが得られている場合にはどうしようもありません。
実験研究とは異なり割り付けがランダム化されていない方法は観察研究と呼ばれます。
現実問題では、観察データが多いこともあり、その場合は別のアプローチを試す必要があるのです。
そんな別のアプローチの1つが層別解析というわけです。
それではそんな層別解析について見ていきましょう!
層別解析とは?
少し前の「年収と一日の摂取カロリー」というデータを考えて見ましょう。
年収と摂取カロリーの二つの上流には年齢という交絡因子が存在するために疑似相関が現れてしまいました。

そこで、例えば、20代・30代・40代・50代・60代以上で層別化してみると、それぞれ層の中のデータでは相関はないことがわかります。
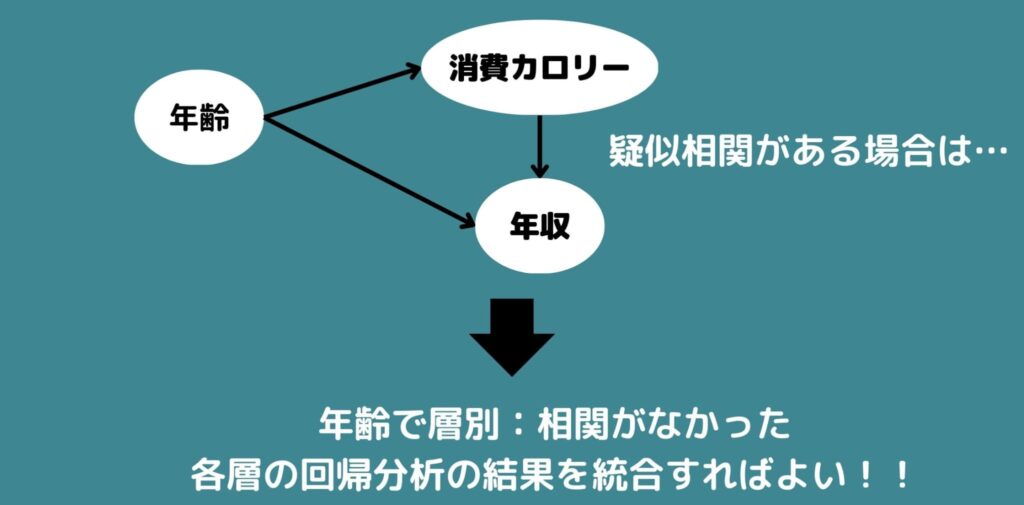
もし、層別して交絡因子を取り除いても原因変数と結果変数に直接的な因果関係があれば各層の中で単回帰分析を行い、各層での回帰係数を統合することで因果効果を推定することが出来ます。
層別解析をPythonで実装
それでは実際に層別解析をPythonで実装していきましょう!
今回は血圧を下げるサプリの効果があるのかないのか確かめるケースを考えてみます。
まず、血圧を下げるサプリを試したい人を公募で募集し、彼らに血圧を下げるサプリを試して、それをサプリを摂取していない一般人と比較しました。
そう、そもそも年齢が高く血圧が高い人ほど血圧を下げるサプリを飲みたいと思い応募してきている可能性が高く、比較対象には年齢という交絡因子が存在することが考えられます。
この誤った実験設定をそのままPythonコードに落とし込んでいきましょう!
# --- データ生成 ---
N_obs = 1000
Age_obs = np.random.normal(50, 10, size=N_obs)
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# 年齢が高いほどサプリを飲みやすい
p_supp_obs = sigmoid(0.3 * (Age_obs - 50))
Supplement_obs = np.random.binomial(1, p_supp_obs)
BloodPressure_obs = 130 + 0.3*Age_obs - 4.0*Supplement_obs + np.random.normal(0, 5, size=N_obs)
df_obs = pd.DataFrame({
'Age': Age_obs,
'Supplement': Supplement_obs,
'BloodPressure': BloodPressure_obs
})
# --- まずは「年齢を無視」して単純比較 ---
mean_bp_supp_obs = df_obs[df_obs['Supplement'] == 1]['BloodPressure'].mean()
mean_bp_nosupp_obs = df_obs[df_obs['Supplement'] == 0]['BloodPressure'].mean()
diff_obs_naive = mean_bp_supp_obs - mean_bp_nosupp_obs
print(f"サプリ群 平均血圧: {mean_bp_supp_obs:.2f}")
print(f"非サプリ群 平均血圧: {mean_bp_nosupp_obs:.2f}")
print(f"単純比較(サプリ - 非サプリ): {diff_obs_naive:.2f} ")
このコードの流れを見ていきましょう!
課題設定に沿って、1000人を対象に年齢が高いほどサプリを飲みやすいというような条件設定にします。
まず、Age_obs = np.random.normal(50, 10, size=N_obs)の部分で、年齢を平均50・標準偏差10の正規分布に従う形でランダムに1000個生成しています。
続いて、sigmoidでシグモイド関数を定義しています。シグモイド関数はロジスティック回帰などに用いられる関数で、入力の値は0~1の範囲に変換します。
すなわち数値を確率に変換する時に役立ちます。
入力が0の場合は出力は0.5になり、それより小さくなればなるほど0に近づき、大きければ大きいほど1に近づくのです。
今回は年齢を入力にしてサプリを飲む確率値を出力したいので、シグモイド関数を用いているのです。
さて、この関数の入力には0.3 * (Age_obs – 50)を入れているので50歳の人はちょうど0.5の確率が出力されるようになっているわけですね。
ちなみに、たとえば被験者が60歳なら、Age_obs – 50 = 10 となり、計算は 0.3 * 10 = 3 となります。シグモイド関数に3 を入れると約 0.95程度。つまり「ほぼ 95% の確率でサプリを飲む」となるわけです。
逆に40歳なら、Age_obs – 50 = -10 → 0.3 * (-10) = -3となり、sigmoid(−3) は約 0.05。つまり「5% くらいの確率でしかサプリを飲まない」となるわけです。
続いて、Supplement_obs = np.random.binomial(1, p_supp_obs)の箇所では、二項分布に基づいて、確率値からサプリを飲むか飲まないかを0,1で出力しています。
続いて、以下の式では血圧の計測結果を出力しています。
BloodPressure_obs = 130 + 0.3*Age_obs - 4.0*Supplement_obs + np.random.normal(0, 5, size=N_obs)年齢が高ければ高いほど血圧が高くなり、サプリを飲んでいれば血圧が下がるような式になっています。
また個体差を出すために、乱数も発生させて加えています。
この結果をデータフレームに格納し、サプリを摂取した群としていない群の平均を比較してみると・・・結果は以下のようになりました。
サプリ群 平均血圧: 143.09
非サプリ群 平均血圧: 143.28
単純比較(サプリ – 非サプリ): -0.19
本来であればサプリの効果があるはずなのに、ほぼ差がないことが分かります(※今回サプリを飲んでいるか否かで4.0を足しているので、本来であれば単純比較の差が4近くなるはず)。
それではこちらに対して層別解析をおこなって結果がどうなるか見ていきましょう!
使うデータは今まで使ってきたものと同じです。
# 年齢を4分割して層を作り、それぞれの層で
# (サプリあり vs なし) の平均差を求め、最後に加重平均をとる。
df_obs['Age_bin'] = pd.qcut(df_obs['Age'], q=4, labels=False)
strata_effects = []
strata_sizes = []
for bin_label in sorted(df_obs['Age_bin'].unique()):
subset = df_obs[df_obs['Age_bin'] == bin_label]
mean_bp_supp_stratum = subset[subset['Supplement']==1]['BloodPressure'].mean()
mean_bp_nosupp_stratum = subset[subset['Supplement']==0]['BloodPressure'].mean()
# サプリ - 非サプリ
effect = mean_bp_supp_stratum - mean_bp_nosupp_stratum
strata_effects.append(effect)
strata_sizes.append(len(subset))
weights = np.array(strata_sizes) / np.sum(strata_sizes)
overall_effect_strat = np.sum(np.array(strata_effects) * weights)
for i, e in enumerate(strata_effects):
print(f"層 {i} の効果(サプリ - 非サプリ): {e:.2f} (サンプル数={strata_sizes[i]})")
print(f"層別加重平均(サプリ - 非サプリ): {overall_effect_strat:.2f} (ちゃんと効果が出る)")
具体的にコードの中身を見ていきましょう!
まず、pd.qcut(df_obs[‘Age’], q=4, labels=False)の部分では年齢を元に全体のデータを0〜25%点、25%点〜50%点、50%点〜75%点、75%点〜100%の4つのグループに分割しています。
続いて、以下の箇所で4つのグループを1つずつ取り出して、グループごとにサプリを飲んでる群とサプリを飲んでいない群の平均の差を計算しています。
strata_effects = []
strata_sizes = []
for bin_label in sorted(df_obs['Age_bin'].unique()):
subset = df_obs[df_obs['Age_bin'] == bin_label]
mean_bp_supp_stratum = subset[subset['Supplement']==1]['BloodPressure'].mean()
mean_bp_nosupp_stratum = subset[subset['Supplement']==0]['BloodPressure'].mean()
# サプリ - 非サプリ
effect = mean_bp_supp_stratum - mean_bp_nosupp_stratum
strata_effects.append(effect)
strata_sizes.append(len(subset))この時、sorted(df_obs[‘Age_bin’].unique())の部分ではそれぞれのグループ番号を集計しています。この場合は、[0, 1, 2, 3]となるはずです。
また、重み付け平均を最終的に取るため各グループのサンプルサイズをstrata_sizes.append(len(subset))で計算しています。
この場合は、キレイに250ずつに分かれているので明示的に全サンプルサイズを4で割ってもよいかもしれません。
最終的に以下の箇所で、各グループの平均値とサンプルサイズを元に重み付け計算をしています。
weights = np.array(strata_sizes) / np.sum(strata_sizes)
overall_effect_strat = np.sum(np.array(strata_effects) * weights)
for i, e in enumerate(strata_effects):
print(f"層 {i} の効果(サプリ - 非サプリ): {e:.2f} (サンプル数={strata_sizes[i]})")
print(f"層別加重平均(サプリ - 非サプリ): {overall_effect_strat:.2f}")結果は以下のようになりました。
層 0 の効果(サプリ – 非サプリ): -1.25 (サンプル数=250)
層 1 の効果(サプリ – 非サプリ): -4.72 (サンプル数=250)
層 2 の効果(サプリ – 非サプリ): -3.11 (サンプル数=250)
層 3 の効果(サプリ – 非サプリ): -4.67 (サンプル数=250)
層別加重平均(サプリ – 非サプリ): -3.43
最終的に加重平均の結果は-3.43となり、サプリを飲んだ層の方が平均的に3.43だけ血圧が低いことが分かりました。
本来のサプリの効果である4.0にだいぶ近くなったのが分かると思います。
しかし、この方法にもデメリットがあり層別するとサンプルサイズが減るので各層での推定が不安定になります。
また、交絡因子が連続変量の場合には離散化して層別するのですが、離散化には解析者の恣意性が入ってしまうことも課題として挙げられます。
さらに、測定されていない交絡因子に対しては対処が出来ません。
統計的因果推論には、他にも色々なアプローチがあるので以下の記事でチェックしてみましょう!

層別解析 まとめ
ここまで統計的因果推論の1種のアプローチである層別解析について解説してきました。
RCTが難しい時は、この層別解析が比較的単純にできてオススメです。
ぜひ使えるようになっておきましょう!
統計的因果推論の分野には、他にもたくさんの手法があります。
他の手法について知りたい方は以下の記事でチェックしてみてください!

また冒頭でも紹介しましたが、統計的因果推論について詳しく知りたい方は以下の私のUdemy講座で学べますのでチェックしてみてください!
【初心者向け】統計的因果推論を学びPythonで実装していこう!RCT・層別解析・マッチング法・傾向スコアを学ぼう!

| 【時間】 | 3.5時間 |
|---|---|
| 【レベル】 | 初級 |
統計的因果推論について詳しく知りたいならこのコース!
今なら購入時に「J56MYR9S」という講師クーポンコードを入れると90%オフ以上の割引価格になりますのでぜひご受講ください!
さらに詳しくAIやデータサイエンスの勉強がしたい!という方は当サイト「スタビジ」が提供するスタビジアカデミーというサービスで体系的に学ぶことが可能ですので是非参考にしてみてください!
AIデータサイエンス特化スクール「スタアカ」

| 【価格】 | ライトプラン:1280円/月 プレミアムプラン:149,800円 |
|---|---|
| 【オススメ度】 | |
| 【サポート体制】 | |
| 【受講形式】 | オンライン形式 |
| 【学習範囲】 | データサイエンスを網羅的に学ぶ 実践的なビジネスフレームワークを学ぶ SQLとPythonを組み合わせて実データを使った様々なワークを行う マーケティングの実行プラン策定 マーケティングとデータ分析の掛け合わせで集客マネタイズ |
データサイエンティストとしての自分の経験をふまえてエッセンスを詰め込んだのがこちらのスタビジアカデミー、略して「スタアカ」!!
当メディアが運営するスクールです。
24時間以内の質問対応と現役データサイエンティストによる複数回のメンタリングを実施します!
カリキュラム自体は、他のスクールと比較して圧倒的に良い自信があるのでぜひ受講してみてください!
他のスクールのカリキュラムはPythonでの機械学習実装だけに焦点が当たっているものが多く、実務に即した内容になっていないものが多いです。
そんな課題感に対して、実務で使うことの多いSQLや機械学習のビジネス導入プロセスの理解なども合わせて学べるボリューム満点のコースになっています!
Pythonが初めての人でも学べるようなカリキュラムにしておりますので是非チェックしてみてください!
ウォルマートのデータを使って商品の予測分析をしたり、実務で使うことの多いGoogleプロダクトのBigQueryを使って投球分析をしたり、データサイエンティストに必要なビジネス・マーケティングの基礎を学んでマーケティングプランを作ってもらったり・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践してもらったりする盛りだくさんの内容になってます!
・BigQuery上でSQL、Google Colab上でPythonを使い野球の投球分析
・世界最大手小売企業のウォルマートの実データを用いた需要予測
・ビジネス・マーケティングの基礎を学んで実際の企業を題材にしたマーケティングプランの策定
・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践して稼ぐ





















