遺伝的アルゴリズムについてわかりやすく解説!Pythonで実装していこう!

こんにちは!スタビジ編集部です!
遺伝的アルゴリズムと聞いて、皆さんは何を思い浮かべるでしょうか??
確かに「遺伝」とあるので生物学の話と思った方もいるかもしれませんが、実は最適化のアルゴリズムの一種なんです!
今回はそんな遺伝的アルゴリズムについて、その概要からPythonでの実装方法まで詳しく解説していきます!
以下の動画でも解説していますのであわせてチェックしてみてください!
目次
遺伝的アルゴリズムとは

遺伝的アルゴリズムとは、生物の進化の仕組みに着想を得て作られた最適化のためのアルゴリズムのことです。
具体的には、生物の進化の過程で起きる「環境に適応し、より強い個体が生き残り、環境に適応できない弱い個体は淘汰される」という現象をデータで表現し、より優秀な個体(パラメータ)を見つけていくという仕組みになっています。
つまり、微分などを行う数理最適化とは異なり、終了条件を満たす解が見つかるまで探索を繰り返す発見的な最適化手法であると言えます。
1975年にミシガン大学の John Henry Holland によって提案された比較的古い手法ですが、様々な研究や改良が重ねられ、現在も活用され続けています。
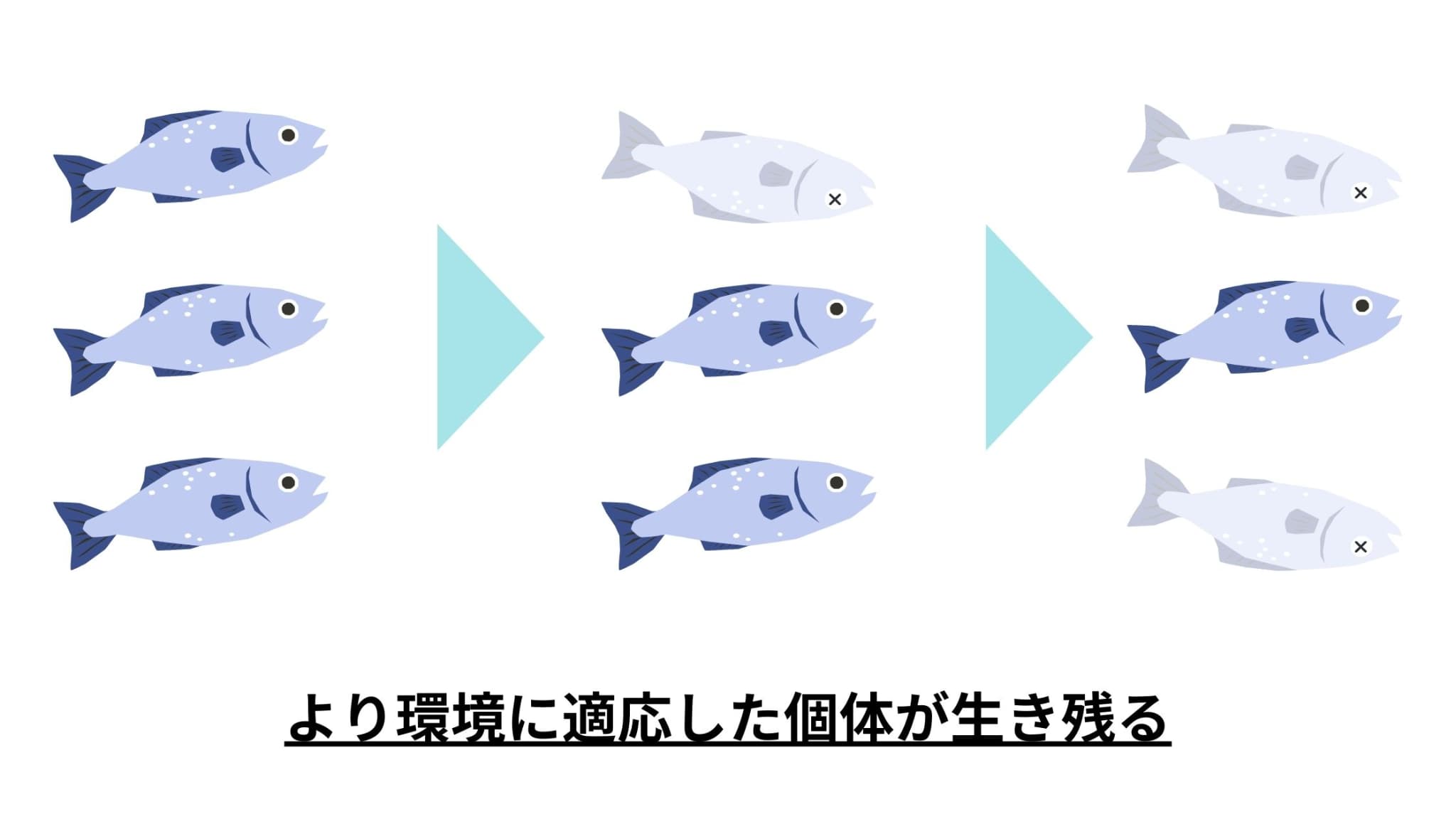
遺伝的アルゴリズムの流れ

ここからは、遺伝的アルゴリズムの流れを具体例を用いて説明していきます。
「ある⚪︎×問題(計10問)があり、8割以上正解の時に合格」という状況を考えます。
1. ランダムに個体(遺伝子)を生成
まず、ランダムに個体(遺伝子)を生成します。
遺伝的アルゴリズムにおける個体とは問題の解(パラメータ)のことであり、今回の状況では第1問から第10問までの解を並べたサンプルがそれにあたります。
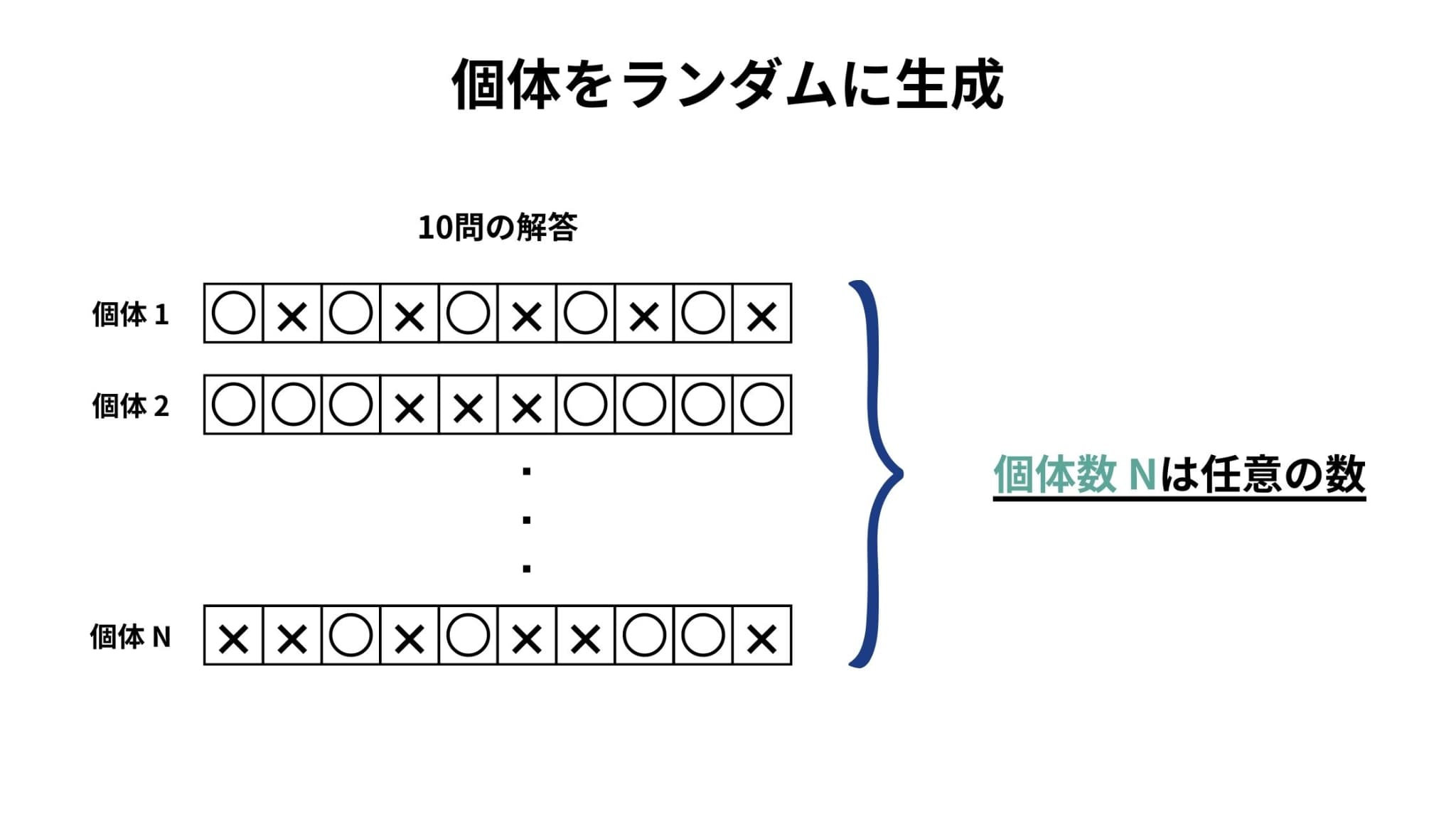
2. 個体の適応度の計算
続いて、個体の適応度を計算していきます。
適応度は問題状況に応じて異なりますが、今回の場合であれば10問中何問正解であるかどうかが適応度となります。
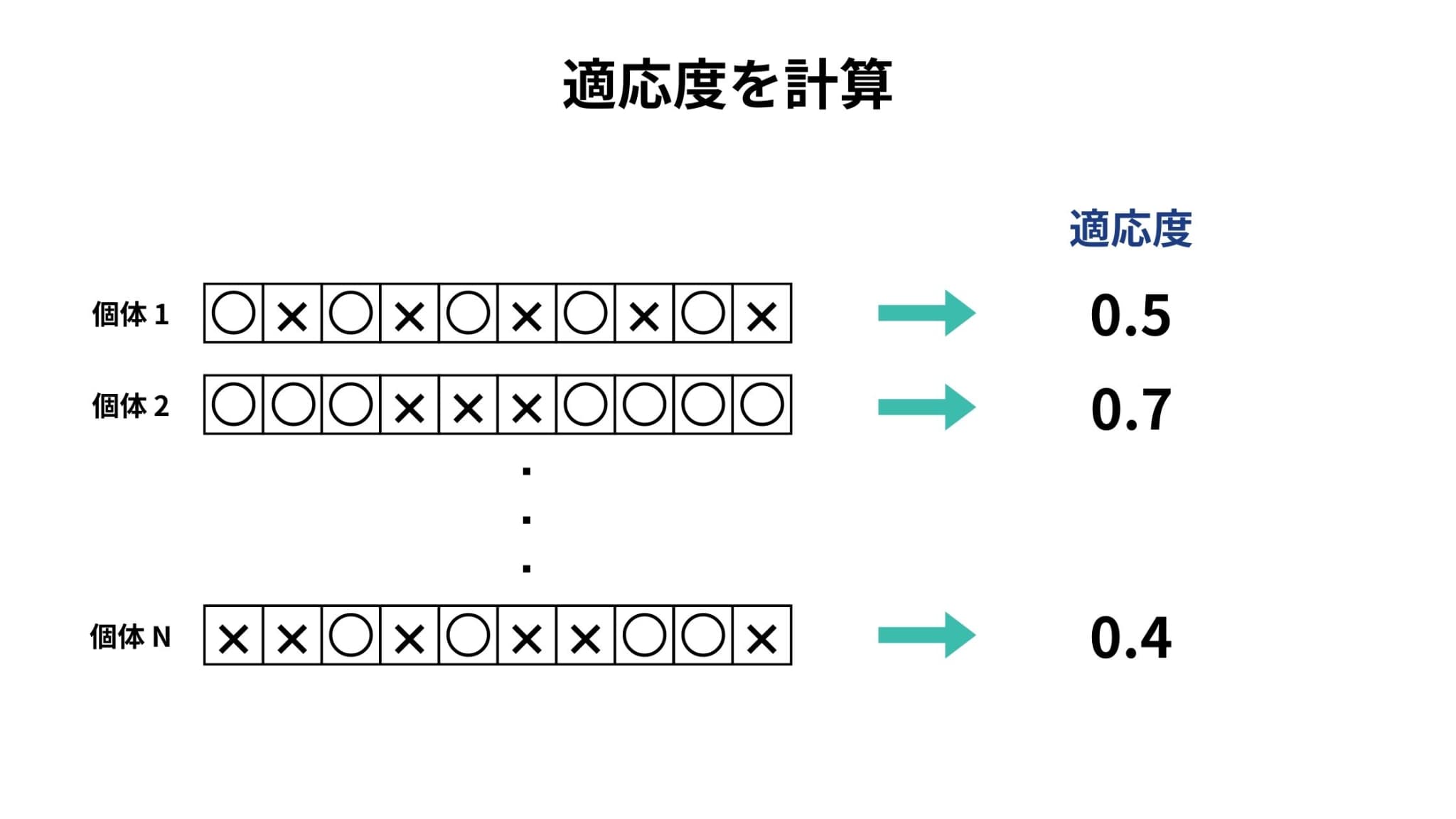
3. 次世代の生成(選択・交叉・突然変異)
この工程が遺伝的アルゴリズムにおいて最も重要です。
ここでは、以下の3つの操作のどれかを行い、次世代の個体を生成します。
1. 個体を2つ選択し、交叉を行う
2. 個体を1つ選択し、突然変異を行う
3. 個体を1つ選択し、そのままコピーする
選択は生物の自然淘汰をモデル化したもので、その名の通り適応度にもとづいて個体を選択する操作のことです。
選択の仕組みには、ルーレット方式やトーナメント方式、エリート方式などがあります。
これらについては次章で解説します。
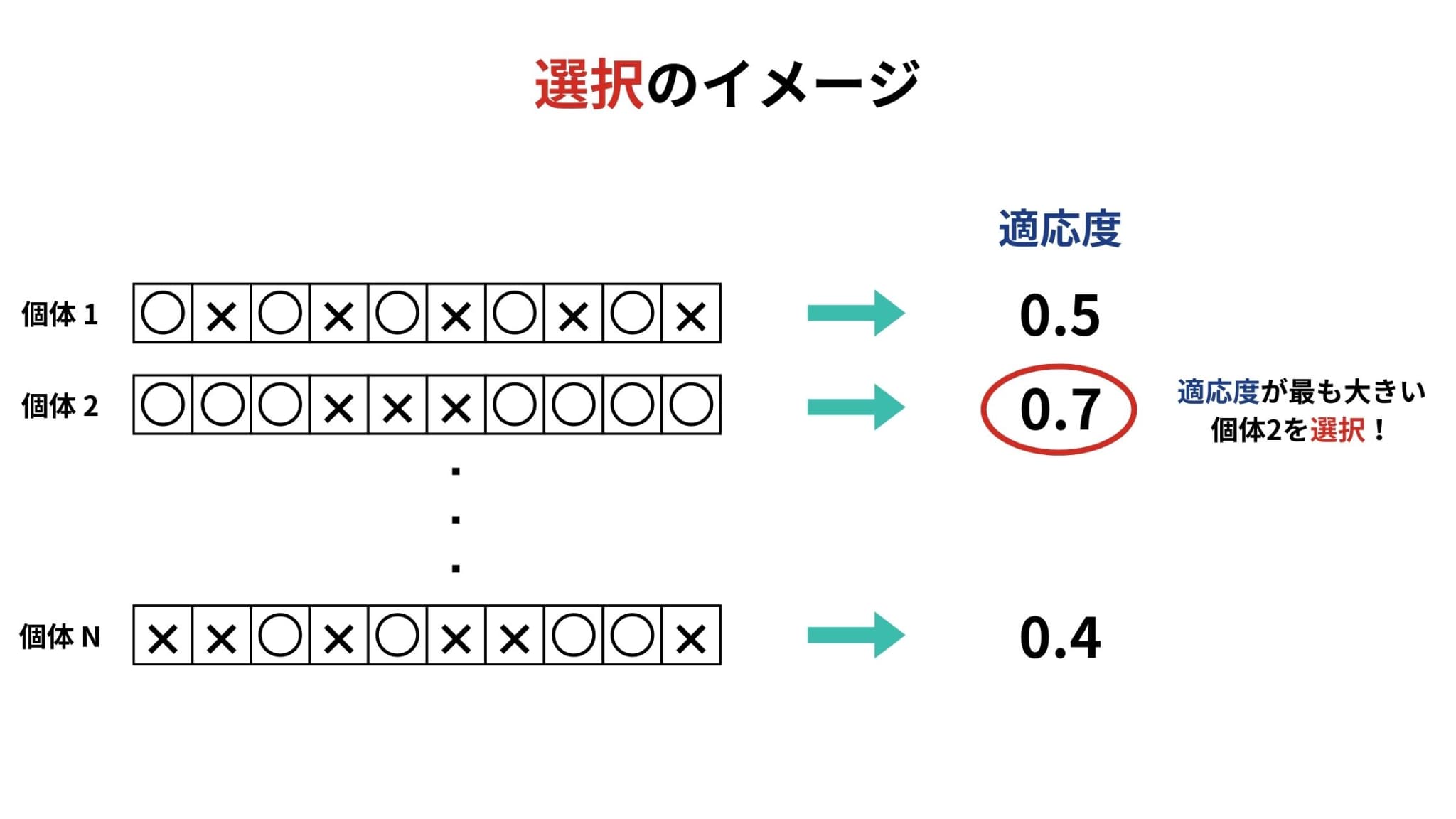
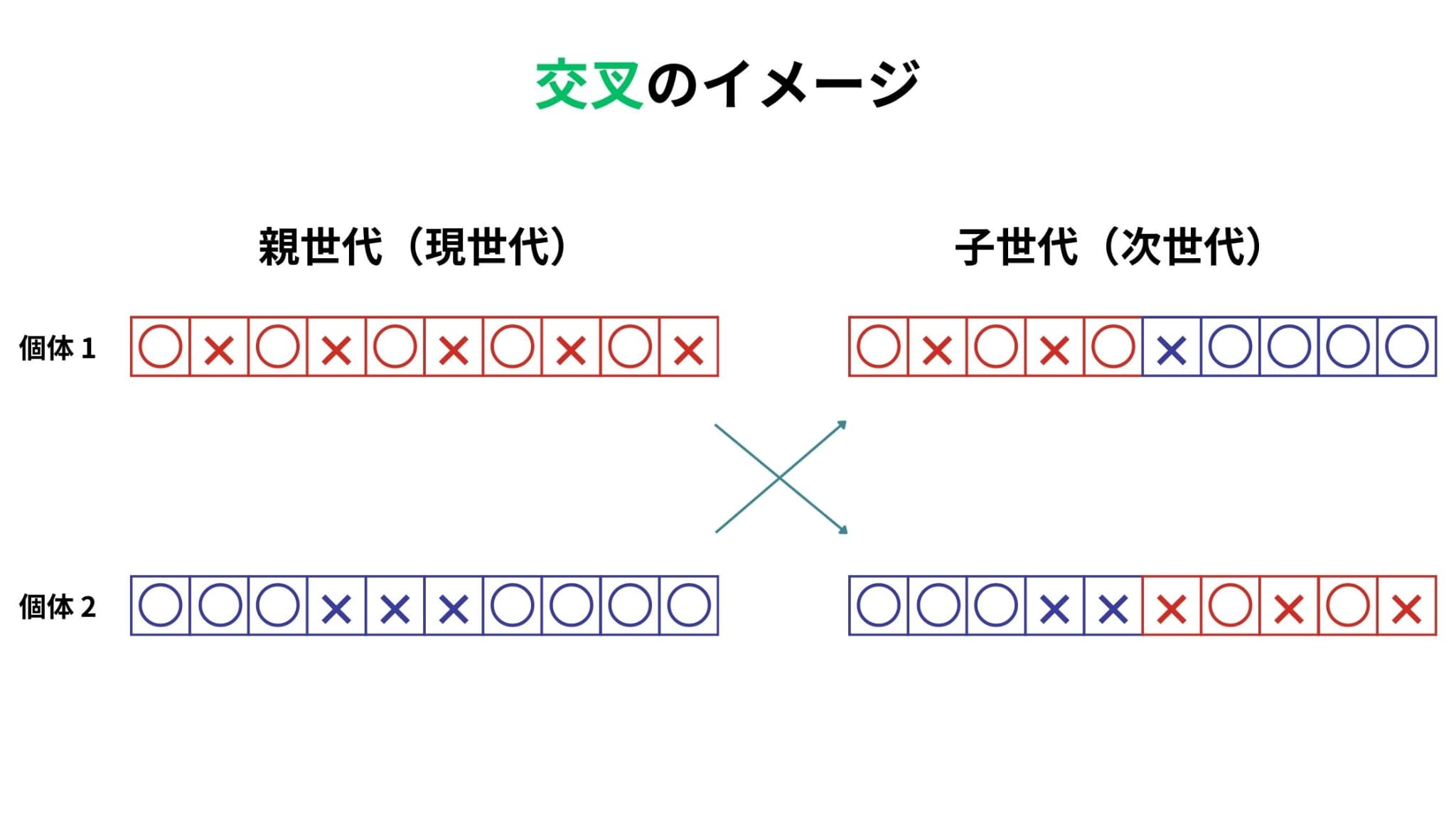
交叉とは、どれか二つの個体を選んで遺伝子の一部を入れ替える操作のことです。
こちらにもいくつか種類があり、一点交叉や二点交叉、一様交叉などがあります。
これらについても次章で解説します。
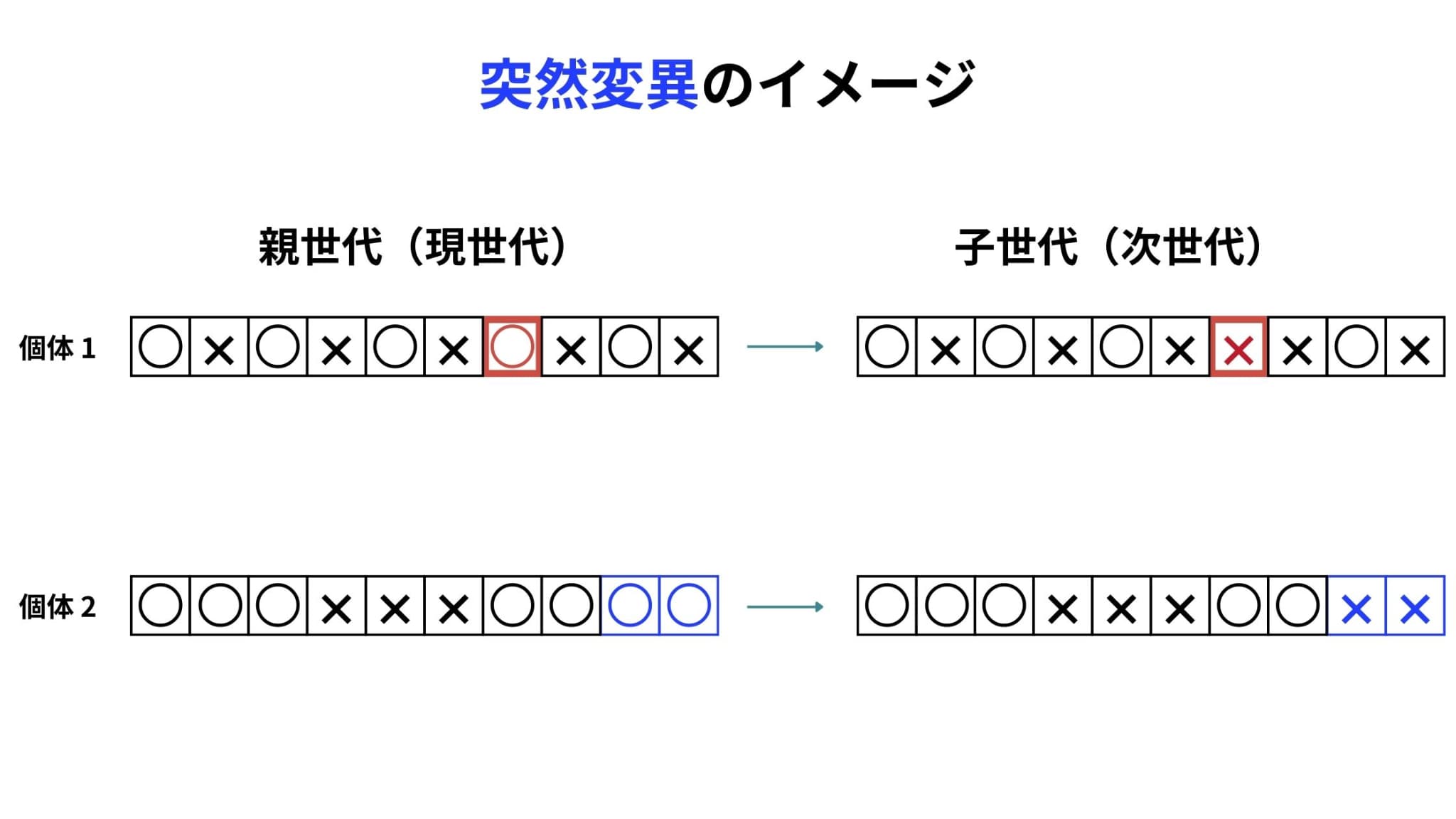
突然変異とは、個体の遺伝子の一部を変化させる操作のことです。
個体の各要素が、事前に指定した確率で変化します。
突然変異の確率は0.1%~1%、高くても数%とされています。
4. 世代交代
3の操作により次世代の個体数が現世代の個体数と同じになった後は、次世代を現世代とします。
これが世代交代です。
5. 最終的な解の決定
3〜4の操作を終了条件を満たすまで繰り返し、最終的な現世代の中で最も適応度が高い個体を解として出力します。
一般的に、「ある回数ループした時」や「個体の適応度がある値を超えた時」(ある回数、ある値は自分で決定)などを終了条件とします。
選択・交叉の仕組み

上で登場した選択・交叉について、それぞれの種類について解説していきます。
1. 選択
上で述べたように、選択にはいくつかの方式が存在します。
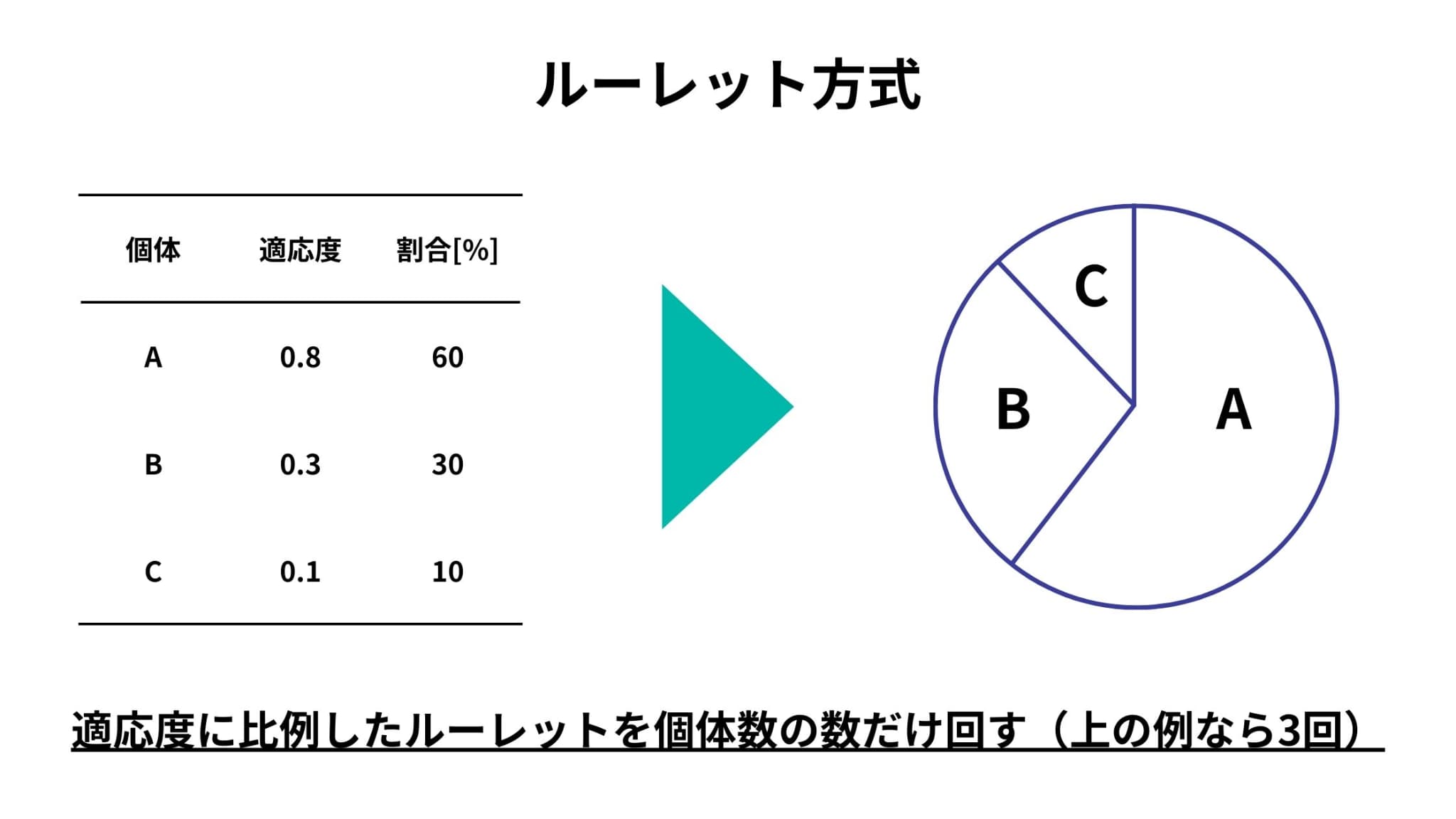
ルーレット方式は代表的な選択方式で、適応度に比例した割合に基づいたルーレットを作成し、そのルーレットを使用してランダムに選択する方法です。
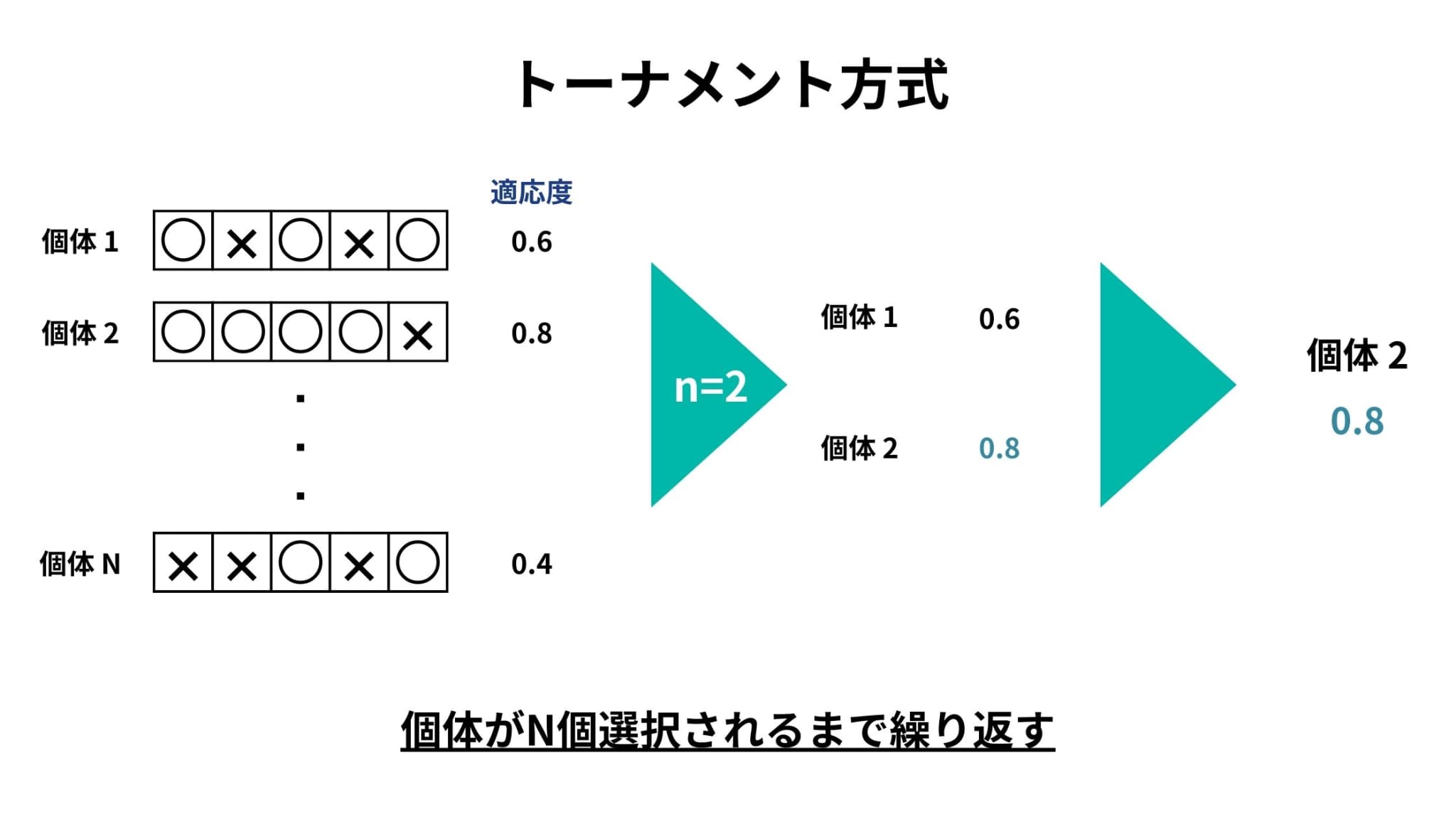
トーナメント方式は、全個体数N個の中から任意のn個の個体(n<N)をランダムに選び、その中で適応度の最も高い個体を選択する方式です。
エリート方式は、全個体の中で適応度の高い(エリート)上位n%を選択する方式です(nは任意の値)。
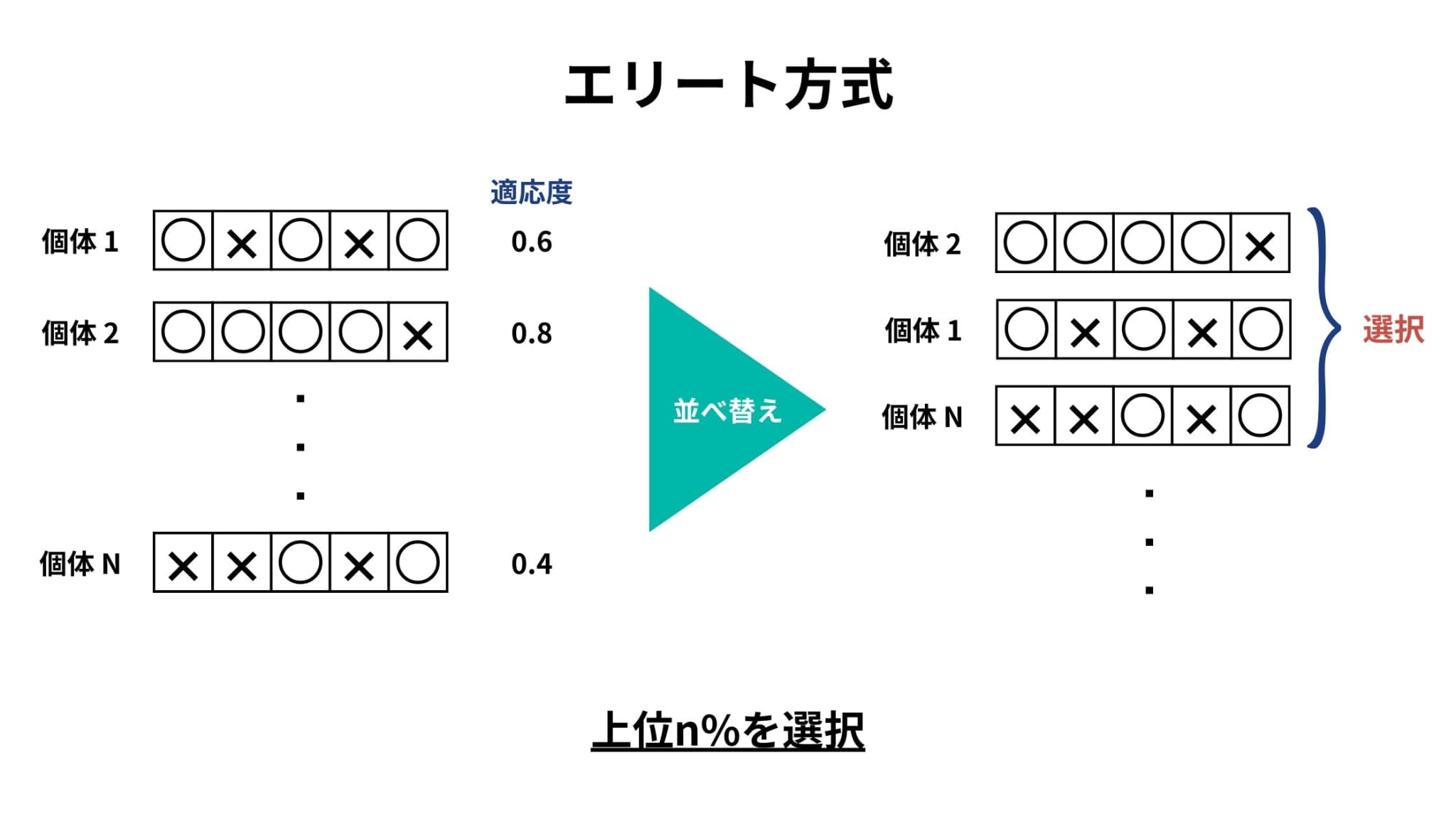
2. 交叉
交叉にもいくつかの種類が存在します。
一点交叉は代表的な交叉の方法で、個体内で切断する要素をランダムに一箇所指定し、その箇所で両親の遺伝子を交換します。
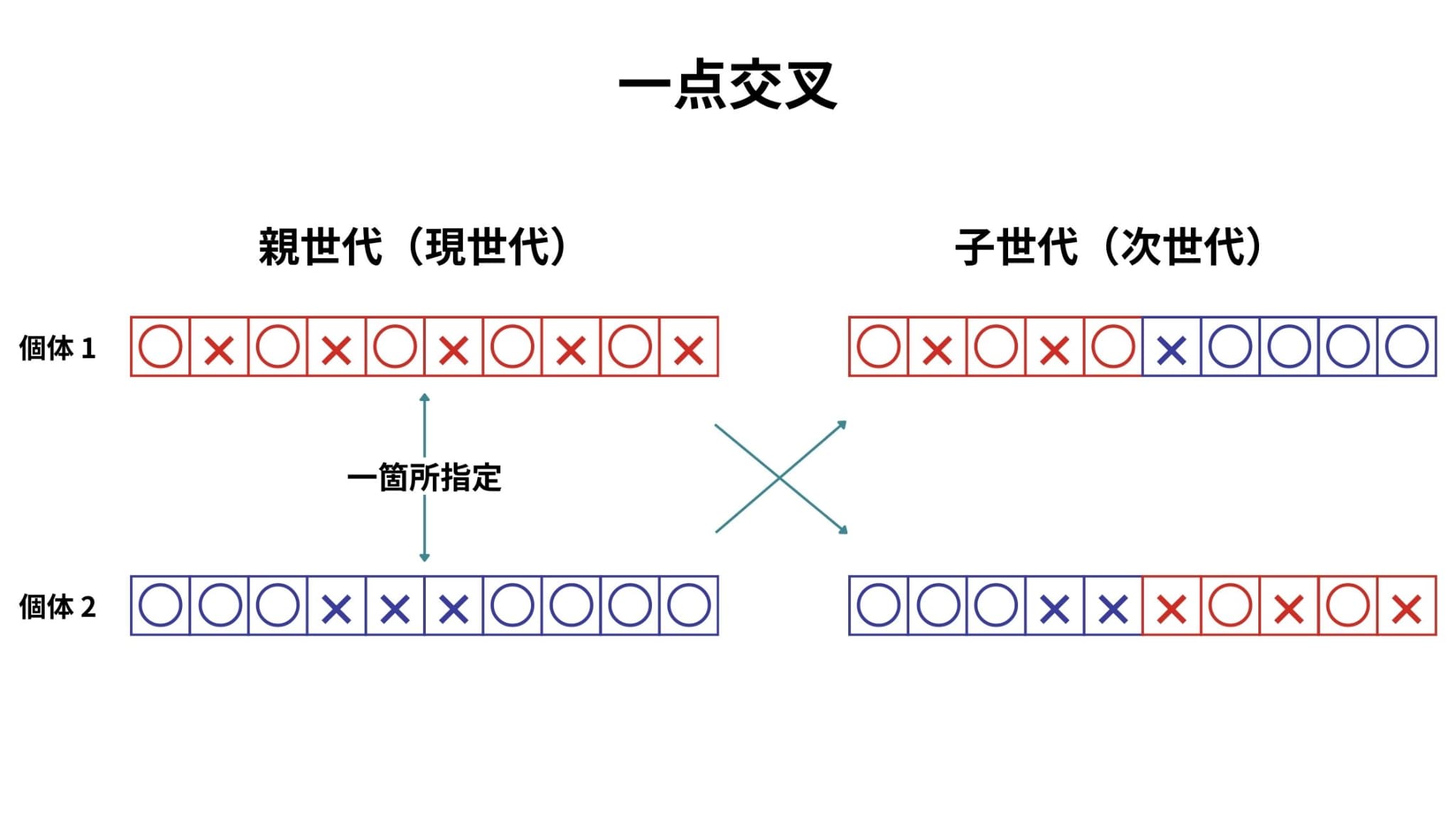
二点交叉は、個体内で切断する要素をランダムに二箇所指定し、その二点で挟まれた部分の遺伝子を交換します。
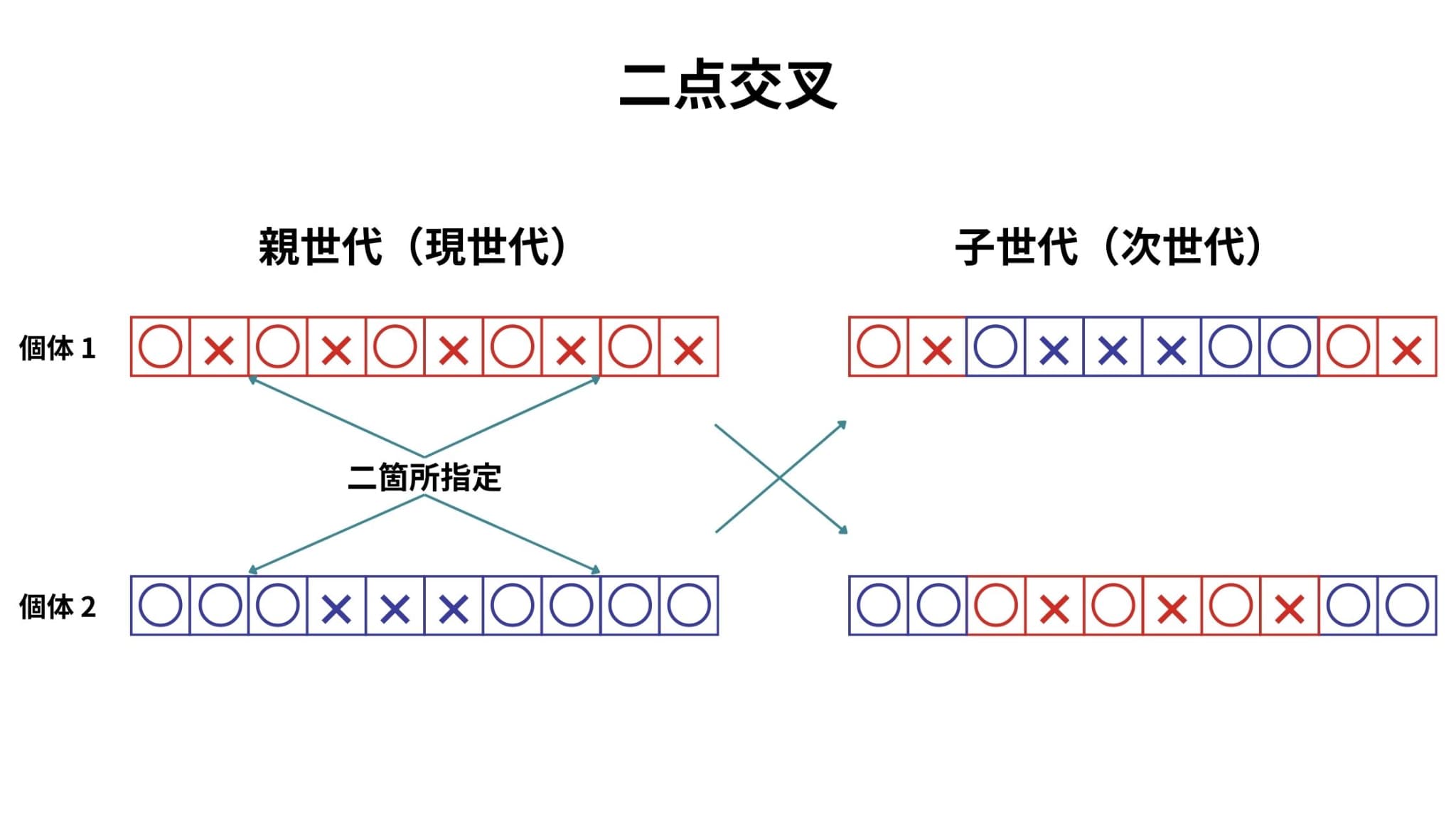
一様交叉は、個体の各要素を独立に1/2の確率で入れ換える方法です。
一般的に、二点交叉が得意とする問題が苦手で、二点交叉と逆の性質を示すことが知られています。
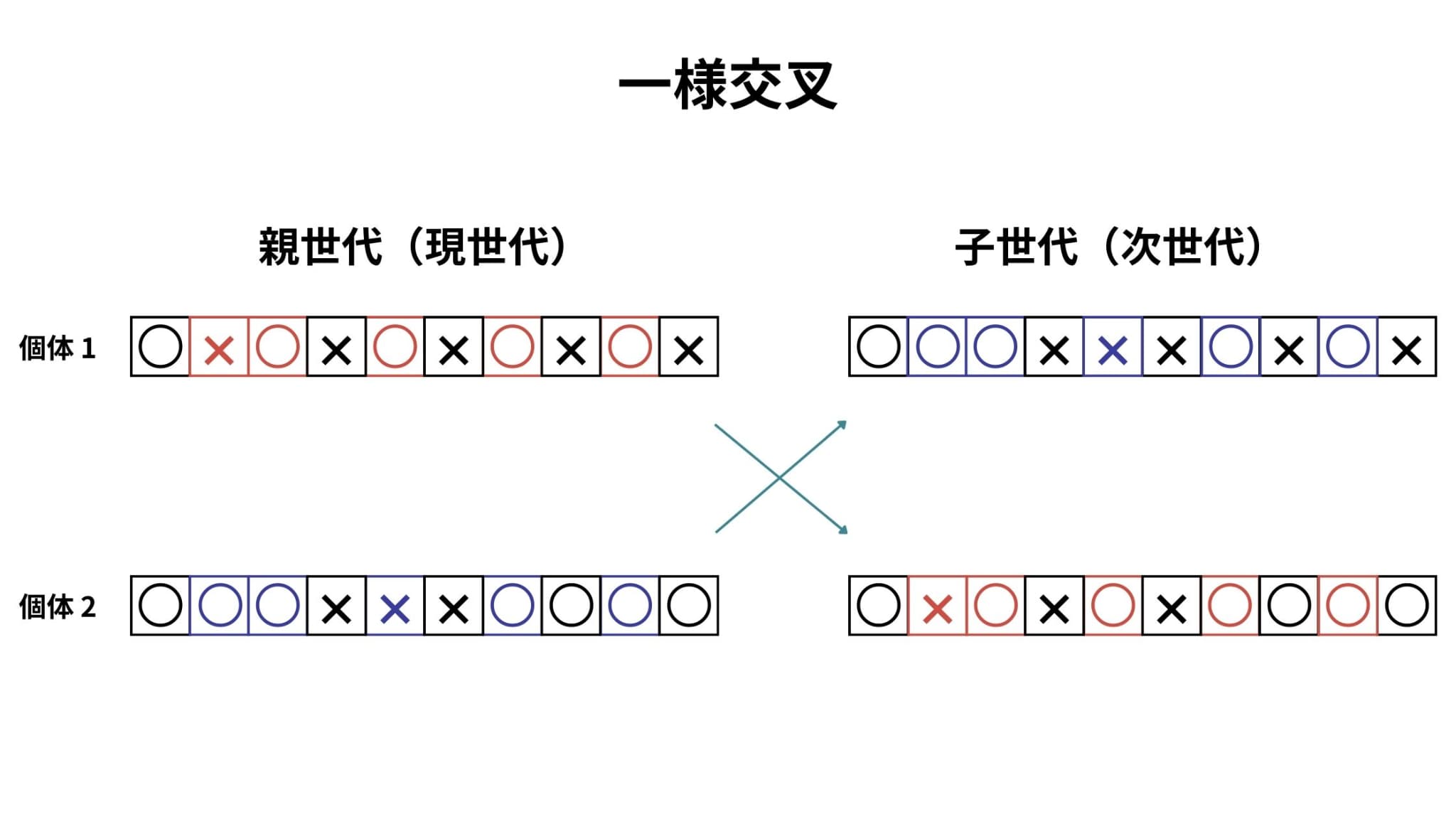
遺伝的アルゴリズムのメリット

ここでは遺伝的アルゴリズムのメリットをいくつか紹介していきます。
1. 汎用性が高い
遺伝的アルゴリズムは、終了条件を満たすまで探索を繰り返す発見的な最適化手法です。
そのため、多少複雑な問題であったとしてもそのままの状態で最適解を探し続けることができます。
ゆえに、様々な分野・問題に応用することが可能です。
2. ランダム性を持つ
遺伝的アルゴリズムは、上記で解説した選択(ルーレット方式やトーナメント方式など)の過程により、ある程度のランダム性を持っています。
ランダム性の活用により、今まで気づかなかったような解を発見できることもあります。
さらに、ランダムであることは可能性を狭めずに検討できることを意味しています。
手法によっては最初の答えに依存するものもありますが、遺伝的アルゴリズムの場合は最初からランダム性があるため、幅広い可能性の中から最適解を探していくことが可能です。
遺伝的アルゴリズムのデメリット

一方で、遺伝的アルゴリズムにはいくつかのデメリットも存在します。
1. 計算時間がかかる
上記の通り、遺伝的アルゴリズムは発見的な最適化手法であるため、終了条件によっては膨大な時間がかかってしまうことがあります。
特に扱うデータが大きいほど時間がかかってしまうので注意しましょう。
2. 最適解の保証ができない
メリットの裏返しにはなりますが、ランダム性を取り入れていることにより、終了条件を満たすまでに最適解に辿り着かない可能性があります。
「遺伝的アルゴリズムを用いれば必ず最適解が得られる!」というわけではないので注意しましょう。
遺伝的アルゴリズムの活用事例

ここでは、遺伝的アルゴリズムの活用事例を2つ紹介していきます。
1. 新幹線の先頭車両の形状

遺伝的アルゴリズムの活用例として、東海道新幹線の先頭車両の形状があります。
2007年に登場したN700系は、東京〜新大阪間の所要時間を従来よりも5分短縮させることに成功しました。
700系の先頭部分は「エアロ・ダブルウィング」と呼ばれ、空気抵抗・微気圧波対策がなされています。
この形状は遺伝子アルゴリズムによって膨大なデザインの中から絞り込まれており、その効果はしっかりと出ました。
2. 人工衛星のアンテナの形状

NASAのニュー・ミレニアム計画の一環として行われた技術試験計画ST5において、衛星に搭載されたアンテナの形状が遺伝的アルゴリズムによって設計されました。
画像を見てみると、かなり変わった形をしていて、私たちが思い浮かべる一般的なアンテナには程遠いデザインであることがわかります。
どのようにしてこのデザインへと進化していったかはわからないですが、様々な項目を満たす効率的な形状を探すために遺伝的アルゴリズムが使われたのでしょう。
遺伝的アルゴリズムをPythonで実装してみよう

ここまで長くなりましたが、ここからはPythonで実際に遺伝的アルゴリズムを実装していきます。
具体的には、遺伝的アルゴリズムを用いてOneMax問題を解いていきます。
OneMax問題とは、[0,0,1,1,0,1,1,0]のように0と1からなる数列の和を最大化する問題です。
以下の流れで分析を進めていきます。
1. ライブラリ(モジュール)のインストール
2. ランダムに個体(遺伝子)を生成
3. 適応度の算出
4. 次世代の生成(選択・交叉・突然変異)
5. 解の決定
6. 遺伝的アルゴリズムの実行
各ステップで関数を作成し、最後に初期値を関数に代入して解を得るという流れとなっています。
1. ライブラリ(モジュール)のインストール
今回はPythonの標準ライブラリであるrandomモジュールのみを使用します。
import random2. ランダムに個体(遺伝子)を生成
次に、個体を生成します。
各個体は、0か1を要素として持つリストとして生成されます。
#個体を生成する関数
def generate_individual(length): #大きさlengthのリスト(0または1がランダムに格納)を生成
return [random.randint(0, 1) for i in range(length)]3. 適応度の算出
続いて、適応度を算出します。
今回はリストの要素の和を適応度とします。
#適応度関数
def fitness_function(individual): #リストの要素の合計値をそのまま適応度として使用
return sum(individual)4. 次世代の生成(選択・交叉・突然変異)
続いて、次世代の生成を行います。
選択はエリート方式、交叉は一点交叉を用いています。
#交叉関数
def crossover(parent1, parent2): #指定された要素インデックスの前後で各遺伝子を入れ替える(一点交叉)
crossover_point = random.randint(0, len(parent1) - 1) #リストの要素インデックスをランダムに指定
child1 = parent1[:crossover_point] + parent2[crossover_point:]
child2 = parent2[:crossover_point] + parent1[crossover_point:]
return child1, child2
#突然変異関数
def mutate(individual, mutation_rate): #個体の各要素が0.1の確率で突然変異を起こす
mutated_individual = []
for bit in individual:
if random.random() < mutation_rate: #0.1の確率
mutated_individual.append(1 - bit) #ビットを反転(0→1または1→0)して格納
else:
mutated_individual.append(bit) #ビットをそのまま格納
return mutated_individual
#次世代を生成する関数
def generate_next_population(current_population, elite_size, mutation_rate):
next_population = []
ranked_population = sorted(current_population, key=lambda x: fitness_function(x), reverse=True) #現世代を適応度の大きい順に並び替える
elite = ranked_population[:elite_size] #上からelite_size個をエリート個体とする
#エリート個体を次の世代に追加(選択)
next_population.extend(elite)
#交叉と突然変異によって新しい個体を生成
while len(next_population) < len(current_population): #現世代と次世代の個体数が同じになるまで繰り返す
parent1, parent2 = random.choices(ranked_population, k=2) #ランダムに2個体を選択
child1, child2 = crossover(parent1, parent2) #交叉
child1 = mutate(child1, mutation_rate) #child1を突然変異
child2 = mutate(child2, mutation_rate) #child2を突然変異
next_population.extend([child1, child2])
return next_population5. 解の決定
そして、上記のステップを終了条件を満たすまで繰り返し、最終的な解を決定します。
#遺伝的アルゴリズムのメイン関数
def genetic_algorithm(population_size, elite_size, mutation_rate, generations, chromosome_length):
population = [generate_individual(chromosome_length) for i in range(population_size)] #population_sizeの数だけ個体を生成
for i in range(generations): #指定した世代数だけ次世代の生成を繰り返す
population = generate_next_population(population, elite_size, mutation_rate)
# 最終世代の中で最も適応度が高い個体を選択
best_individual = max(population, key=lambda x: fitness_function(x))
best_fitness = fitness_function(best_individual)
return best_individual, best_fitness #最終世代の出力6. 遺伝的アルゴリズムの実行
初期値を設定し、5で定義したアルゴリズムを用いて実行していきます。
#パラメータの設定
population_size = 100 #個体数
elite_size = 10 #エリートの数
mutation_rate = 0.1 #突然変異が生じる確率
generations = 50 #世代数
chromosome_length = 20 #ビット列の長さ
#遺伝的アルゴリズムの実行
best_solution, best_fitness = genetic_algorithm(population_size, elite_size, mutation_rate, generations, chromosome_length)
print("Best solution:", best_solution)
print("Best fitness:", best_fitness)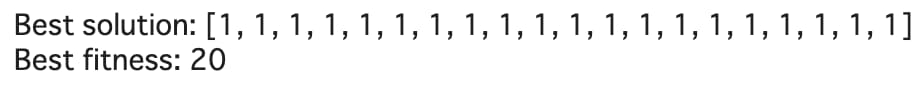
全ての要素が1である個体が最適解として出力されました。
適応度も20であり、長さが20である個体(ビット列)の最適解であることがわかります。
つまり、遺伝的アルゴリズムを用いてOneMax問題を解くことができました。
まとめ
ここまでご覧いただきありがとうございました!
今回は遺伝的アルゴリズムの概要からPythonでの実装方法まで解説していきました。
遺伝的アルゴリズムは、比較的古い手法ながら様々な問題・分野に応用できる強力な手法です。
最適化手法を適用したいけどどんな手法を用いるべきかわからない!という方は、まずは遺伝的アルゴリズムから試してみましょう!
また、今回分析に用いたPythonについて勉強したい方は以下の記事を参考にしてみてください!

さらに詳しくAIやデータサイエンスの勉強がしたい!という方は当サイト「スタビジ」が提供するスタビジアカデミーというサービスで体系的に学ぶことが可能ですので是非参考にしてみてください!
AIデータサイエンス特化スクール「スタアカ」

| 【価格】 | ライトプラン:1280円/月 プレミアムプラン:149,800円 |
|---|---|
| 【オススメ度】 | |
| 【サポート体制】 | |
| 【受講形式】 | オンライン形式 |
| 【学習範囲】 | データサイエンスを網羅的に学ぶ 実践的なビジネスフレームワークを学ぶ SQLとPythonを組み合わせて実データを使った様々なワークを行う マーケティングの実行プラン策定 マーケティングとデータ分析の掛け合わせで集客マネタイズ |
データサイエンティストとしての自分の経験をふまえてエッセンスを詰め込んだのがこちらのスタビジアカデミー、略して「スタアカ」!!
当メディアが運営するスクールです。
24時間以内の質問対応と現役データサイエンティストによる複数回のメンタリングを実施します!
カリキュラム自体は、他のスクールと比較して圧倒的に良い自信があるのでぜひ受講してみてください!
他のスクールのカリキュラムはPythonでの機械学習実装だけに焦点が当たっているものが多く、実務に即した内容になっていないものが多いです。
そんな課題感に対して、実務で使うことの多いSQLや機械学習のビジネス導入プロセスの理解なども合わせて学べるボリューム満点のコースになっています!
Pythonが初めての人でも学べるようなカリキュラムにしておりますので是非チェックしてみてください!
ウォルマートのデータを使って商品の予測分析をしたり、実務で使うことの多いGoogleプロダクトのBigQueryを使って投球分析をしたり、データサイエンティストに必要なビジネス・マーケティングの基礎を学んでマーケティングプランを作ってもらったり・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践してもらったりする盛りだくさんの内容になってます!
・BigQuery上でSQL、Google Colab上でPythonを使い野球の投球分析
・世界最大手小売企業のウォルマートの実データを用いた需要予測
・ビジネス・マーケティングの基礎を学んで実際の企業を題材にしたマーケティングプランの策定
・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践して稼ぐ























