シューハート管理図では、正常状態での平均値と標準偏差を用いて管理限界線を引き、各期で異常検知を行います．
しかしそれでは、非常に微小な変化が起こった時、それを誤差として判断してしまう可能性が高いです。
その点EWMA管理図では、微小な変化に対する検知を可能にしています。
EWMA管理図
実際にどのようなことを行っているのか、図で見てみましょう！
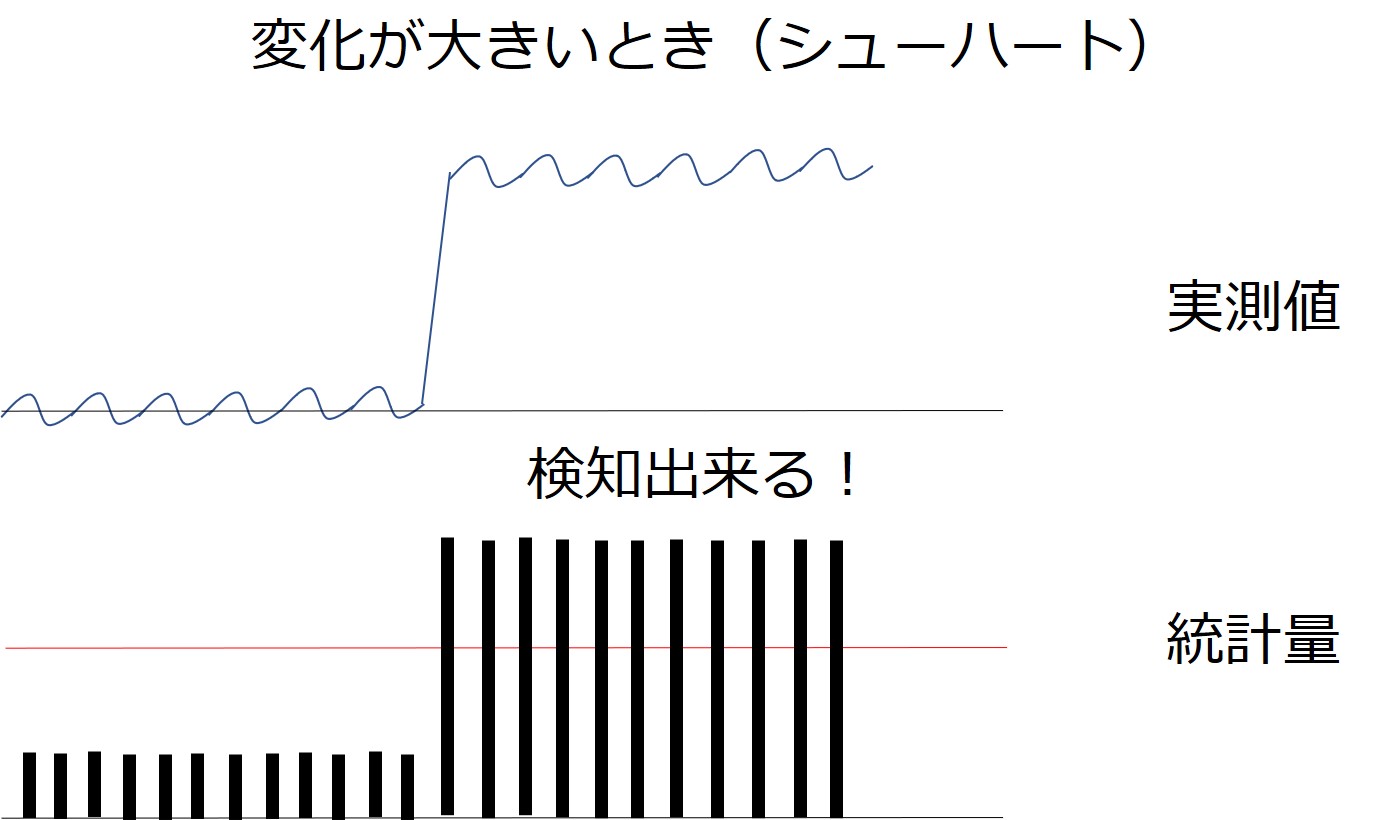
そもそもの工程の変化が大きいときは、シューハート管理図でも検知できます。
しかし、工程の変化が小さくなると・・・
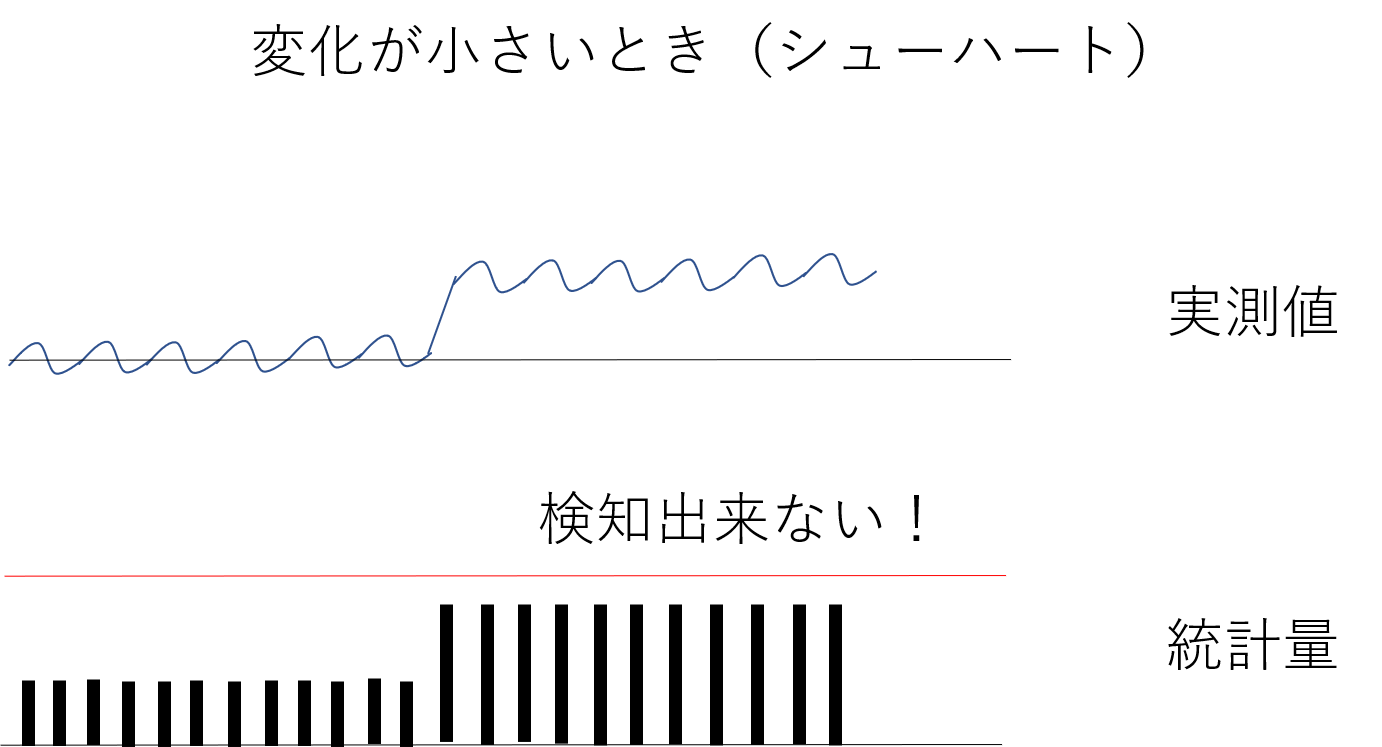
管理限界線を越えないので検知できません。
しかし微小な変化が続いているので、工程の状態が変化しているのは間違いありません。
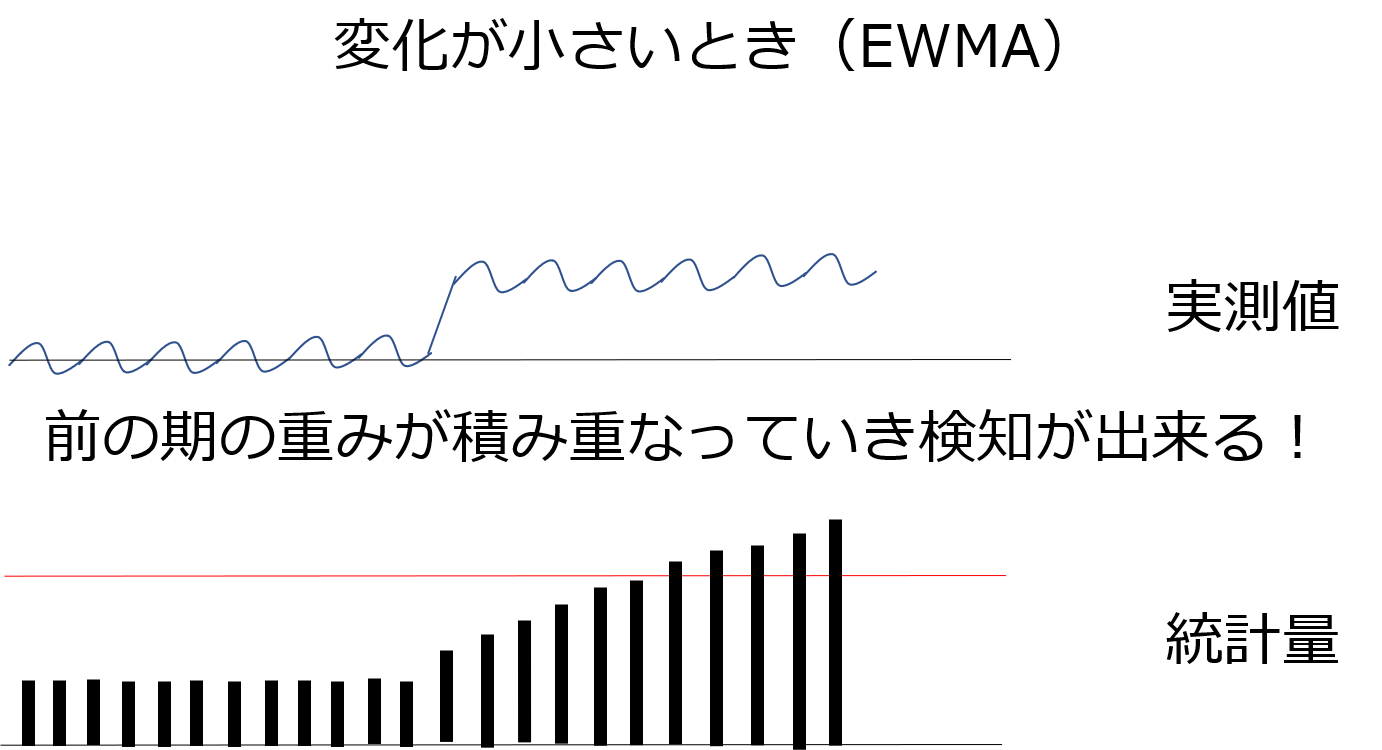
そこで前の期に重み付けをして足し合わせ微小な変化が積み重なった時に変化として検知しようという手法が登場します。それがEWMA管理図です。
ちなみに期ごとの差分を足し合わせる手法であるCUSUM管理図はEWMA管理図の少し前に提案されました。しかし、一般的にはEWMA管理図の方が精度が良い場合が多く、よく用いられています。
EWMA管理図の具体的な計算方法
では具体的に計算方法を見ていきましょう！
まずある変数\(x_t\)が以下のような正規分布に従っているとします。
$${x_t}\sim{N}({\mu_0}, {{\sigma_0}^2})$$
この時\(\lambda\)に基づいて指数的な重みづけを行います。
$${w_t}=(1-\lambda){w_{t-1}}+\lambda(x_t-\mu_0), w_0=\mu_0$$
\(w_t\)はEWMAの統計量であり、これを更新していきます。
そしてこの時の上限管理限界線と下限管理限界線を以下のように求めます！
$$UCL=\mu_0+h\sigma{\sqrt{\frac{\lambda}{1-\lambda}}}$$
$$LCL=\mu_0-h\sigma{\sqrt{\frac{\lambda}{1-\lambda}}}$$
この時、\(h\)は管理限界線の幅を表すパラメータです。
そしてこの管理限界線を超えたら異常と判断するわけです！
EWMA管理図 まとめ
いかがだったでしょうか？
管理図は日本をはじめとした多くの国で工程管理の場で実用的に使われている手法です。
より発展的な内容を知りたい方は多変量管理図についてみて見てください！
もし管理図について勉強したいなら以下の書籍がオススメです！
EWMA管理図とCUSUM管理図について比較している良書です！
また、以下の記事で他の管理図についてまとめていますので良ければごらんください！
スタビジのコンテンツをさらに深堀りしたコンテンツが動画と一緒に学べるスクールです。
プレミアムプランでは私がマンツーマンで伴走させていただきます！ご受講お待ちしております！
