こんにちは！
データサイエンティストのウマたん(@statistics1012)です！
管理図は、工程管理など多くの現場で良く用いられています。
ここでは、そんな管理図の中で一番重要かつ最も良く用いられている管理図、”シューハート管理図” について見ていきましょう！
シューハート管理図とは？
管理図とは、工程が正常状態なのか異常状態なのかを判断するために用いられる手法です。
その中でも最もシンプルで全ての管理図の基本となるシューハート管理図は非常に重要なので覚えておきましょう！
シューハート管理図では、正常状態から得られた母平均と母分散をもとに現在の状態が正常であるか異常であるか考えます。
この時、管理図の中心線をCL、ギリギリ超えてはいけない上の限界線をUCL(上側管理限界線)、下の限界線をLCL(下側管理限界線)と呼びます。
これらの管理線は以下のように計算されます。
\(CL=\mu\)
\(UCL=\mu+3\sigma\)
\(LCL=\mu-3\sigma\)
品質の世界では管理限界線には\(3\sigma\)法と呼ばれ、\(3\sigma\)を用いることが一般的です。
これは正常の状況下で0.3%の確率で管理限界線を超える計算になります!!
つまり1000個の製品に関して3個の不良品が混ざっている具合！
Rを使ってシューハート管理図を描いてみよう！
それでは、そんなシューハート管理図をRで実装してみましょう！
##母平均と母分散
mu <- 2
sig <- 1
##正常状態
a <- rnorm(20,mu,sig)
##異常状態
b <- rnorm(10,4,sig)
##異常状態2
c <- rnorm(10,mu,2)
koutei <- c(a,b,c)
CL <- mu
UCL <- mu+3*sig
LCL <- mu-3*sig
plot(koutei,type="b",ylab="観測値",ylim=c(-2,6))
abline(h=CL)
abline(h=UCL,col=2)
abline(h=LCL,col=2)1～20期までは正常状態で、21～30期は平均が大きく変化しています。31～40期では分散が大きく変化しています。
これらをもとにCL、UCL、LCLを計算し管理図を描画すると以下のようになります！
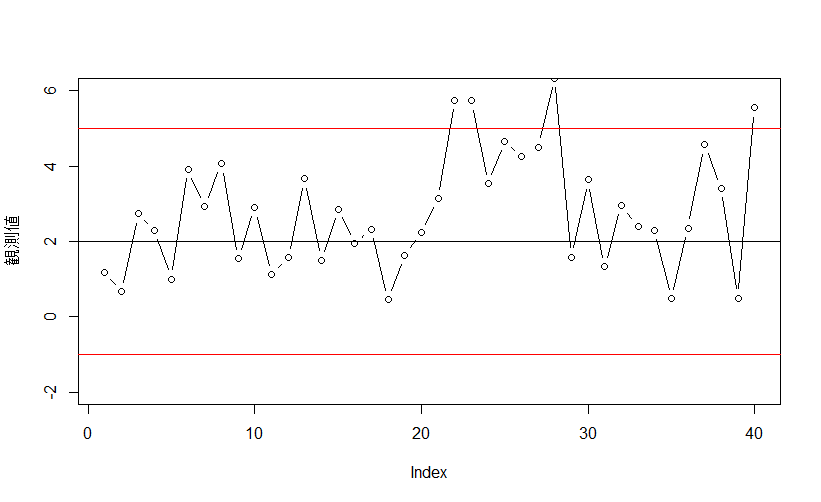
上側と下側に存在するのがUCLとLCLです。
21～30期も無事検知に成功、31期～40期も検知に成功しています！
ちなみに、異常と判断する基準はUCL、LCLを超えたらというだけではありません。
たとえば7回連続で片方の側に打点が続くなどした場合異常と判定します！
ここまでシューハート管理図に関してお話してきましたが、シューハート管理図という言葉自体はそれほどメジャーではないし重要ではありません。
シューハート管理図の概念をしっかり頭にいれ、シューハート管理図の1手法である\(\bar{X}-R\)管理図や\(\bar{X}-s\)管理図という名前を覚えておきましょう！
それでは、そんな\(\bar{X}-R\)管理図とはなんなのでしょうか？
\(\bar{X}-R\)管理図とは？
さきほどのシューハート管理図の例では、1期あたり1サンプルでしたが、一般的には1期ごとにいくつかのサンプルが存在することが多いです。
これを群またはサブグループと呼びます。
\(\bar{X}-R\)管理図や\(\bar{X}-s\)管理図などはこのサブグループありの管理図に用いられる手法になります。
群の中での特性値、平均\(\bar{X}\)と範囲\(R\)を計算し、それらの特性値ごとに管理図を描いて管理するというものです。\(\bar{X}\)管理図と\(R\)管理図の二つで管理します。
先ほどのシューハート管理図における\(\sigma\)は決められた係数によって計算します。(省略)
\(\bar{X}-s\)管理図は、この範囲Rが標準偏差sになったもの！何も難しくありませんね！
管理図を使いこなして、工程の異常を検知しましょう！
シューハート管理図 まとめ
管理図の中で最も定番のシューハート管理図についてまとめてきました！
ここで紹介したのは非常にシンプルな単変量管理図ですが、多変量管理図などの発展的な内容も載せているので以下の記事をご覧ください！
シューハート管理図から一歩踏み込んだ管理図を勉強するなら以下の書籍がオススメです！
管理図は異常検知手法の一種です。
異常検知を勉強するのにおすすめな本を以下にまとめています！
また、統計学や機械学習・データサイエンス、Pythonに興味のある方は以下の記事でまとめていますので是非チェックしてみてください！
スタビジのコンテンツをさらに深堀りしたコンテンツが動画と一緒に学べるスクールです。
プレミアムプランでは私がマンツーマンで伴走させていただきます！ご受講お待ちしております！
