こんにちは！
消費財メーカーでデータサイエンティストをやってるウマたん(@statistics1012)です。
時系列分析の中で必ず出てくる「定常性」という概念。
時系列データ分析に関しては以下の記事もあわせてご覧ください。
MAモデルからARIMAモデルまでについて簡単に紹介しています。
その中で、定常性という概念が出てきて、MAモデルは常に定常であり、ARモデルはある条件のもとで定常になると説明しました。
また定常性を持った時系列データのことを定常過程と呼び、定常でないデータのことを非定常過程と呼びます。
この記事では、そんな定常性という概念についてもう少し詳しく説明します。
定常性
弱定常性の定義は以下の通り。
\begin{eqnarray}
\left\{
\begin{array}{l}
E(y_t)&=&\mu\\
Cov(y_t,y_{t-k})&=&E[(y_t-\mu)(y_{t-k}-\mu)]\\
\end{array}
\right.
\end{eqnarray}
平均や自己共分散が時点\(t\)に依存していません。
次に、強定常性の定義は以下の通りになります。
\begin{eqnarray}
f(y_{t_1+k},y_{t_2+k},\cdots,y_{t_m+k})=f(y_{t_1},y_{t_2},\cdots,y_{t_m})
\end{eqnarray}
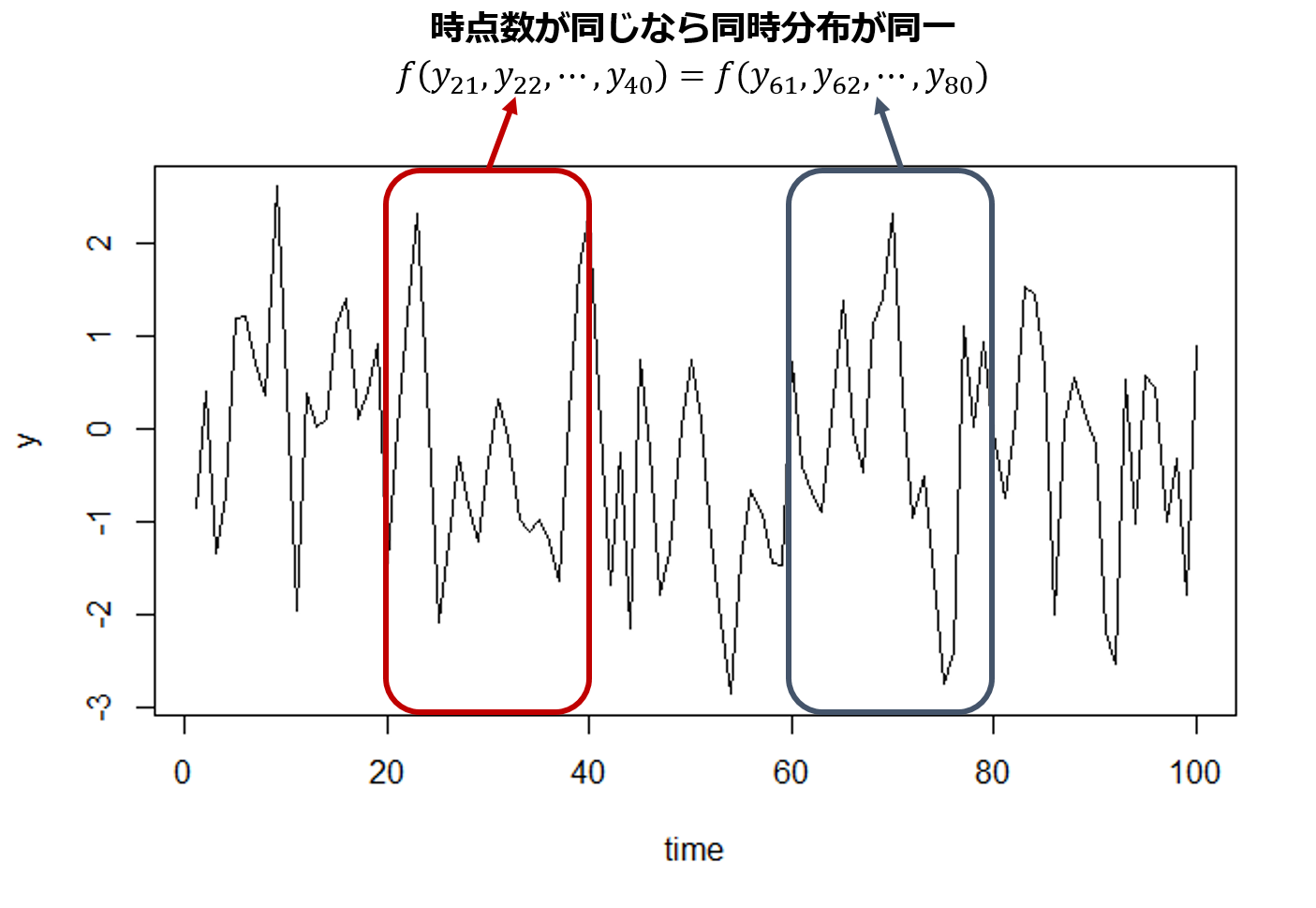
つまり、時点の数が同じならどの集まりの同時分布も同一であるということです。
同時密度関数が多変量正規分布で記述出来る場合、多変量正規分布は平均ベクトルと共分散行列で特定されるため弱定常性を満たせばそのまま強定常性を満たすことになります。
まあ、強定常性という概念はあるもののあまり使われることはないので「定常」というワードが出たら弱定常性のことだと思って大丈夫です。
それでは次にモデルの定常性についてみていきましょう。
各モデルでの定常性
まず、MAモデルから確認しましょう。
定数項を省いた場合の\(q\)次のMAモデルの定義は次の通りでした。
\begin{eqnarray}
y_t&=&\epsilon_t+\theta_1\epsilon_{t-1}+\theta_2\epsilon_{t-2}+\cdots+\theta_q\epsilon_{t-q} ,
\epsilon_t\sim{W.N.(\sigma^2)}
\end{eqnarray}
\(y_t\)の平均、分散および\(y_t\)と\(y_{t-k}\)の自己共分散を求めてみます。
\begin{eqnarray}
E(y_t)&=&E(\epsilon_t+\theta_1\epsilon_{t-1}+\theta_2\epsilon_{t-2}+\cdots+\theta_q\epsilon_{t-q})\\
&=&E(\epsilon_t)+\theta_1E(\epsilon_{t-1})+\theta_2E(\epsilon_{t-2})+\cdots+\theta_qE(\epsilon_{t-q})\\
&=&0+\theta_1\times0+\theta_2\times0+\cdots+\theta_q\times0\\
&=&0\\
V(y_t)&=&V(\epsilon_t+\theta_1\epsilon_{t-1}+\theta_2\epsilon_{t-2}+\cdots+\theta_q\epsilon_{t-q})\\
&=&V(\epsilon_t)+\theta_1^2V(\epsilon_{t-1})+\theta_2^2V(\epsilon_{t-2})+\cdots+\theta_q^2V(\epsilon_{t-q})\\
&=&(1+\theta_1^2++\theta_2^2+\cdots+\theta_q^2)\sigma^2\\
Cov(y_t,y_{t+k})&=&E[(\epsilon_t+\theta_1\epsilon_{t-1}+\theta_2\epsilon_{t-2}+\cdots+\theta_q\epsilon_{t-q})(\epsilon_{t+k}+\theta_1\epsilon_{t+k-1}+\theta_2\epsilon_{t+k-2}+\cdots+\theta_q\epsilon_{t+k-q})]\\
&=&
\left\{
\begin{array}{l}
(1+\sum_{j=1}^{q}\theta_j^2)\sigma^2, k=0\\
(\theta_k+\sum_{j=k+1}^{q}\theta_j\theta_{j-k})\sigma^2, 1 \leq k \leq q\\
0, k \geq q+1\\
\end{array}
\right.
\end{eqnarray}
となり、平均、分散、自己共分散ともに時点\(t\)には依存しないため常に弱定常性を保ちます。
次にARモデルの場合について説明します。
定数項を省いた場合の\(p\)次のARモデルの定義は次の通りでした。
\begin{eqnarray}
y_t=\phi_1{y_{t-1}}+\phi_2{y_{t-2}}+\cdots+\phi_p{y_{t-p}}+\epsilon_t,
\epsilon_t\sim{W.N.(\sigma^2)}
\end{eqnarray}
このARモデル弱定常性を持つための必要十分条件は次の特性方程式の解の絶対値が全て1より大きいことです。
\begin{eqnarray}
1=\phi_1B+\phi_2B^2+\cdots+\phi_pB^p
\end{eqnarray}
例えば、1次のARモデルでは特性方程式は
\begin{eqnarray}
1=\phi_1B
\end{eqnarray}
となるので、
\begin{eqnarray}
1&=&\phi_1B\\
|B|&>&1 \Leftrightarrow \left|\frac{1}{\phi}\right|>1 \Leftrightarrow |\phi|<1\\
\end{eqnarray}
が条件となります。
次に、Rを用いて定常や非定常なデータを実際に発生させてみます。
定常性をRで実行
まず、MAモデルで発生させてみましょう。
定数項を省いた以下の２次のMAモデルを用います。
\begin{eqnarray}
y_t=\epsilon_t+\theta_1\epsilon_{t-1}+\theta_2\epsilon_{t-2} ,
\epsilon_t\sim{W.N.(\sigma^2)}
\end{eqnarray}
用いるコードは次の通りです。
結果は次のようになりました。
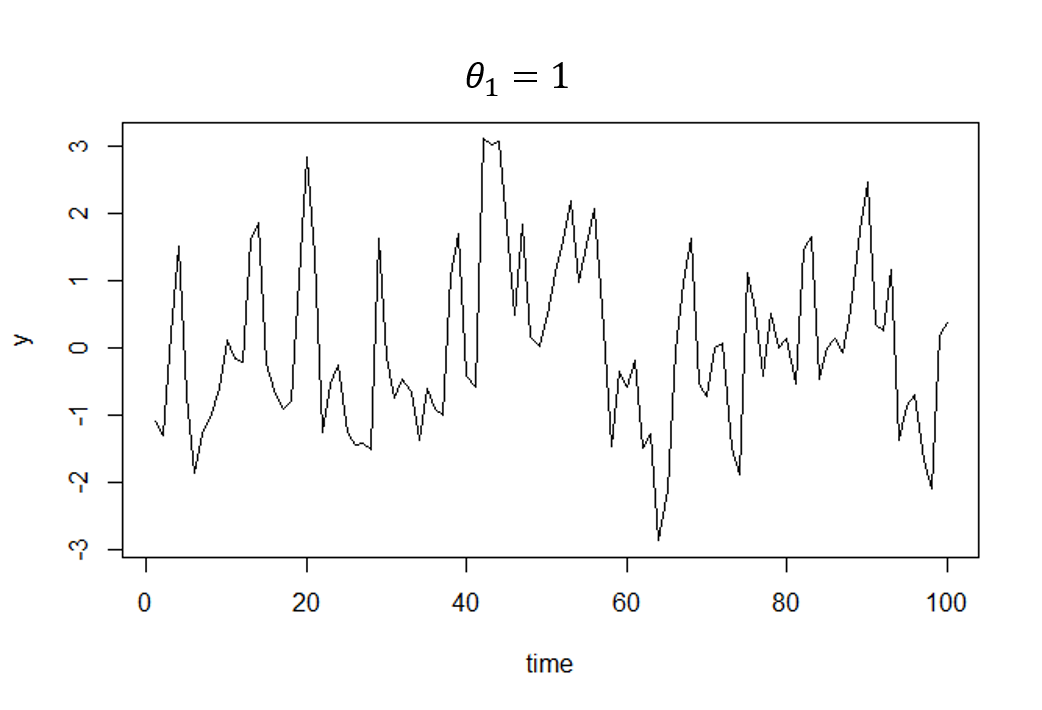
確かに定常過程になっています。
次はARモデルで発生させてみます。
まずは定数項を省いた以下の1次のARモデルを用います。
\begin{eqnarray}
y_t=\phi_1{y_{t-1}}+\epsilon_t,
\epsilon_t\sim{W.N.(\sigma^2)}
\end{eqnarray}
用いるコードは次の通りです。
結果は次の通りです。
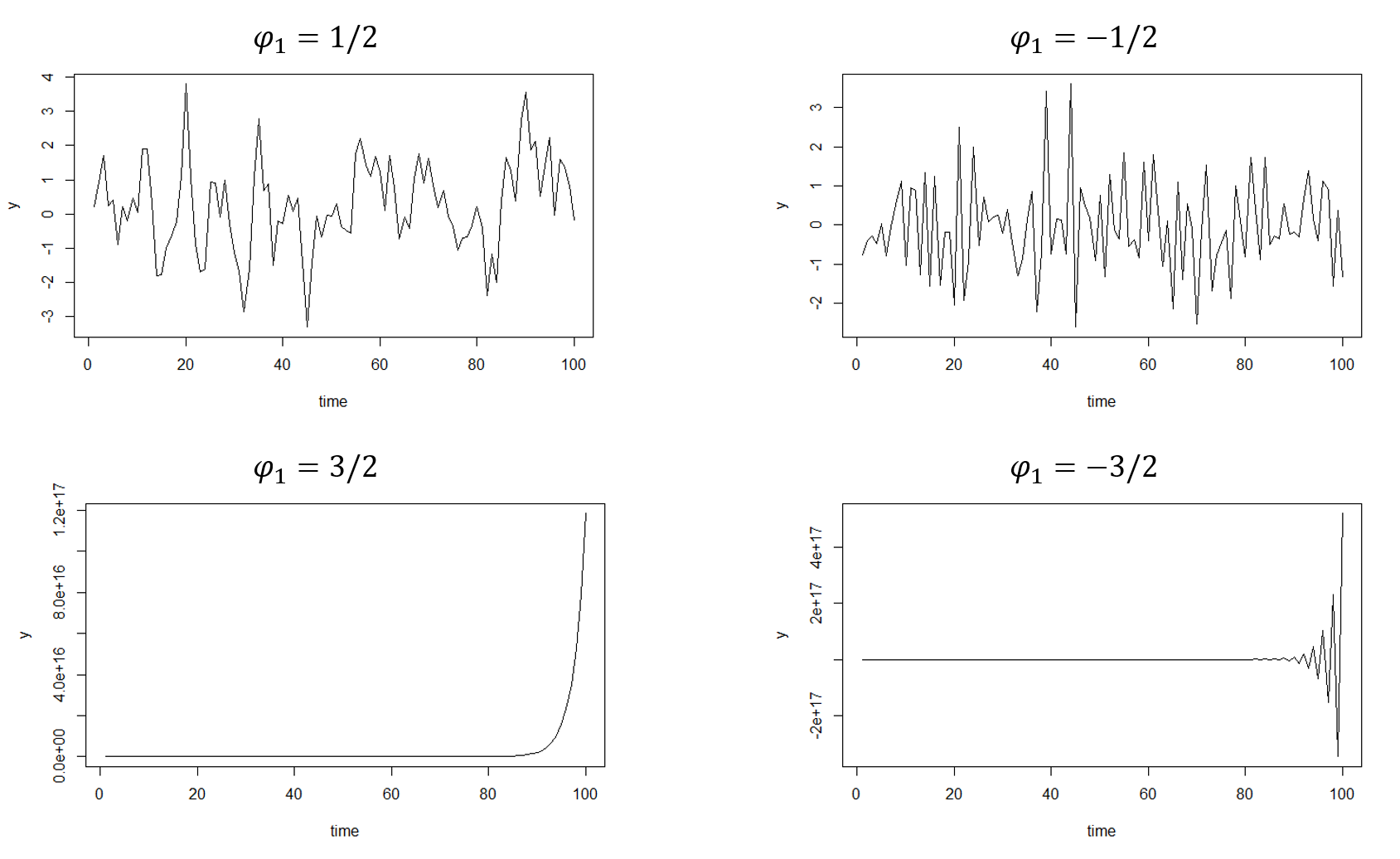
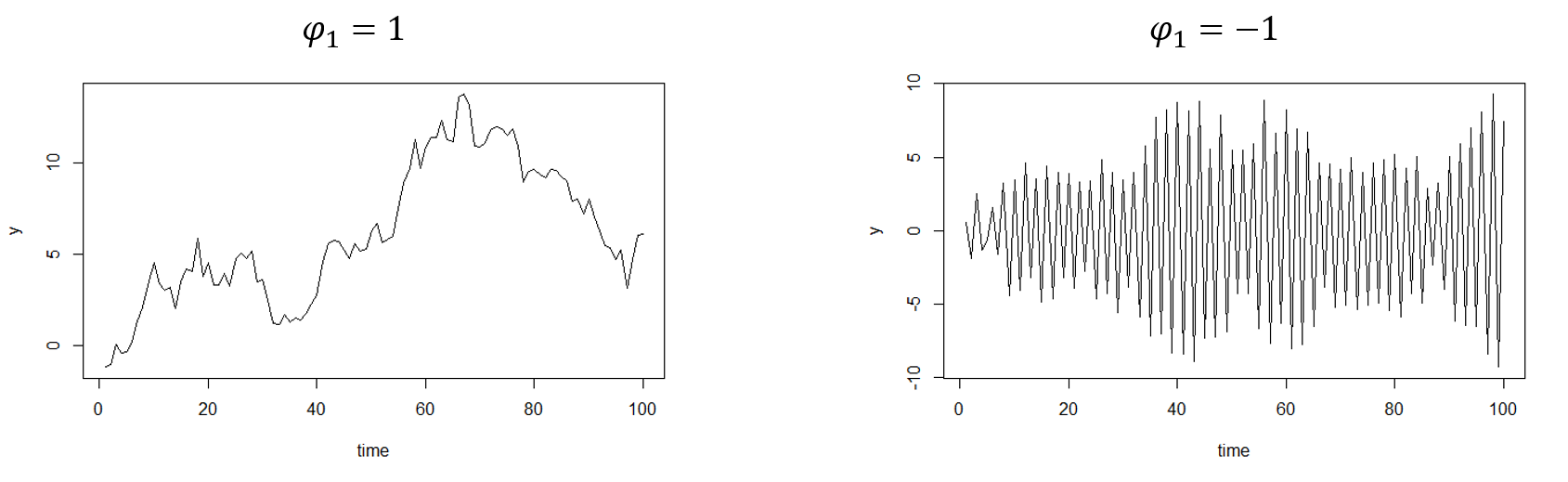
どうでしょうか。確かに、\(|\phi_1|<1\)のときには定常過程になっていることが分かります。
\(\phi_1=3/2\)のときには一つの方向に発散しています。
\(\phi_1=-3/2\)のときには上下に振動しながら分散が大きくなって発散しています。
\(\phi_1=-1\)のときには上下に振動しながら分散が変化しています。平均に収束することはありません。
\(\phi_1=1\)のときには分散は発散していきそうですが、平均については発散しないため分析から外すべきなのかプロットからでは判断が難しいです。このような過程を単位根過程(unit root process)と呼びます。
単位根過程
さて、上記で単位根過程というワードが出てきたのでその定義と扱いについて説明します。
単位根過程の説明は次の通りです。
「\(p\)次ARモデルで特性方程式の\(d\)個の根が1となる場合にその確率過程は\(d\)次の和分過程\(I(d)\)と表現する。」
先ほどの1次のARモデルでは
\begin{eqnarray}
1&=&\phi_1B\\
B&=&1 \Leftrightarrow \phi_1=1\\
\end{eqnarray}
のときに単位根過程となり\(I(1)\)と表現します。
また2次のARモデルで例えば\(\phi_1=1/2,\phi_2=1/2,\)ならば
\begin{eqnarray}
1&=&\frac{1}{2}B+\frac{1}{2}B^2 \Leftrightarrow (B-1)(B+2)=0
\end{eqnarray}
となるので、\(I(1)\)である。
また、同じく2次のARモデルで\(\phi_1=2,\phi_2=-1\)ならば
\begin{eqnarray}
1&=&2B-B^2 \Leftrightarrow (B-1)^2=0\\
\end{eqnarray}
となるので、\(I(2)\)である。
さて、単位根過程は特殊な非定常過程であり、そのまま解析してはいけません。
そこで、単位根過程かどうかを判定するためにはDickey-Fuller検定を行います。
Rならtseriesパッケージのafd.test()かCADFtestパッケージのCADFtest()で簡単に行うことが出来ます。
では、検定の結果単位根であると考えられるならどうすればいいかというと、差分を取れば単位根過程は定常過程になります。
より正しく言うと\(I(d)\)は\(d\)階の階差を取ると定常過程となります。そのため単位根過程は差分定常過程とも呼ばれます。
例えば、先ほどの\(\phi_1=2,\phi_2=-1\)の和分過程\(I(2)\)で発生させたデータに対して階差を取ってみると次のようになります。
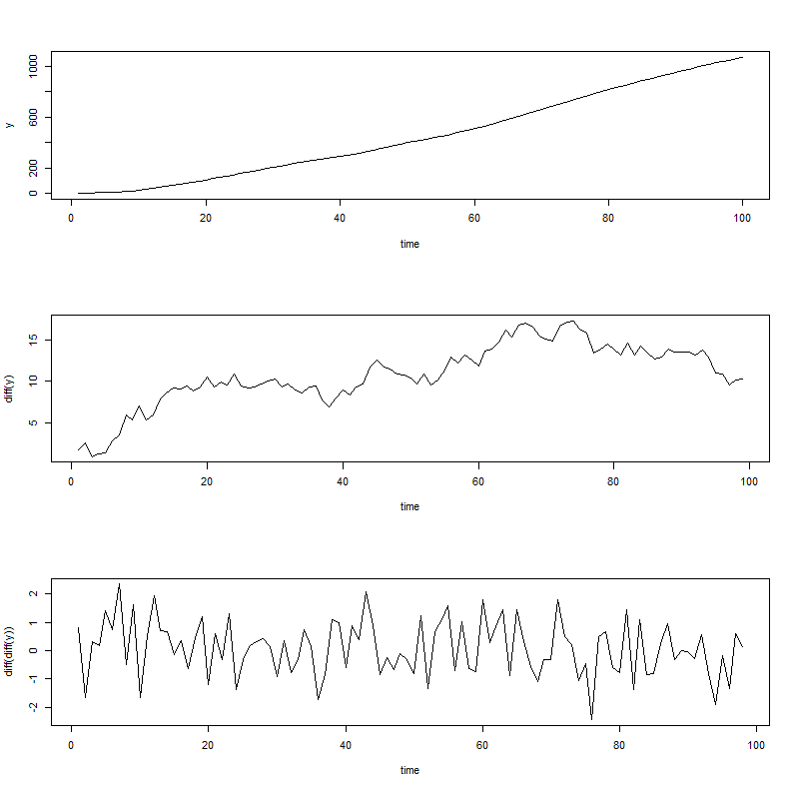
確かに、2階階差で定常過程になっています。
なぜ単位根過程に気を付けなければならないかというと単に非定常過程だからというだけでなく「見せかけの回帰」という厄介な現象が起きる可能性があるからです。
定常性 まとめ
本記事では、定常性についてまとめてきました。
定常性は、時系列分析において非常に重要な概念です。
より詳しく知りたい方は以下の書籍をオススメします。定常・非定常の話も含め時系列データ分析のエッセンスを理論的に学ぶことができます。
少々難解な箇所もあります。
また時系列分析の書籍に関しては以下の記事にまとめているのでそちらもご覧ください！
機械学習、データサイエンスについて学びたい方は以下の記事をチェックしてみてください！
スタビジのコンテンツをさらに深堀りしたコンテンツが動画と一緒に学べるスクールです。
プレミアムプランでは私がマンツーマンで伴走させていただきます！ご受講お待ちしております！
