混合ガウスモデルをわかりやすく解説!Pythonで実装していこう!

こんにちは!スタビジ編集部です!
混合ガウスモデル、皆さんは聞いたことがあるでしょうか??
あまり馴染みのない言葉かもしれませんが、実はクラスタリング手法の一種なんです!
今回はそんな混合ガウスモデルについて、その概要からPythonでの実装方法まで詳しく解説していきます!
以下のYoutube動画でも解説していますのであわせてチェックしてみてください!
目次
混合ガウスモデルとは

混合ガウスモデルとは、クラスタリング手法の一種であり、その名の通り混合ガウス分布(混合正規分布)を基とした手法です。
混合ガウス分布とは、複数のガウス分布(正規分布)が混合している分布のことです。
例えば、手元に日本の成人の身長が男女別に記録されたデータがあるとします。
以下の図は、そのデータを男女別で描いたものです(男性の平均身長を170、女性の平均身長を157としています)。
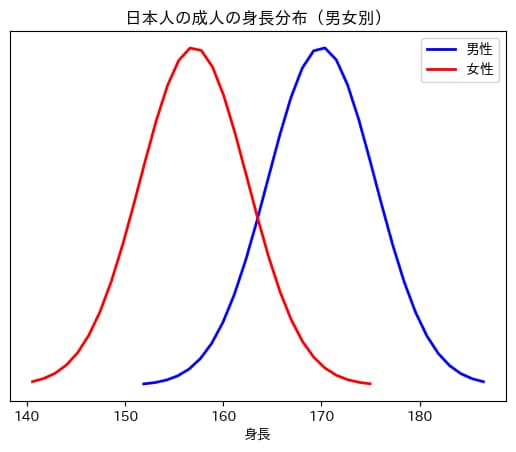
あらかじめ男女別で身長が記録されていれば、上のような分布をそれぞれで描くことができますね。
しかし、もし男女のラベルが身長のデータになかったらどうでしょうか。
どのデータが男性でどのデータが女性かが全くわからないため、以下の図のような分布が描かれることになります。
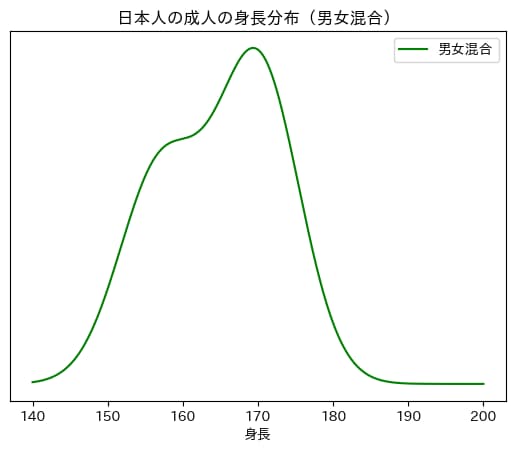
この分布がまさに、2つの正規分布を混合している混合ガウス分布となります。
混合ガウスモデルは、データが複数のガウス分布から生成されていると仮定し、各データがどのガウス分布に所属するかを推定する手法です。
その推定には、最尤推定法を用います。
混合ガウスモデルのメリット

クラスタリング手法には様々なものがありますが、混合ガウスモデルにはどんなメリットがあるのでしょうか。
ここでは大きなメリットを2つ紹介していきます。
メリット①:データの確率密度関数を得ることができる
メリットの一つ目は、データの確率密度関数を得られることです。
確率密度関数を得る = データを確率分布として表現できるということですから、新たにサンプリングを行ったり、回帰分析や分類予測へ応用することができます。
メリット②:クラスター数を自動で決定することができる
メリットの二つ目は、クラスター数を自動で決定できることです。
他のクラスタリング手法ではクラスター数を恣意的に決定することが多いですが、混合ガウスモデルではその必要がありません。
具体的には、BIC(ベイズ情報量基準)が最小となるようなクラスター数を最適なクラスター数とすることができます。
BICについての簡単な説明は、以下の記事のx-means法の部分を参考にしてみてください!
混合ガウスモデルをPythonで実装してみよう

ここからは、Pythonで実際に混合ガウスモデルを実装していきます。
分析の目的は、特徴量を用いてデータを複数のクラスターに分類すること!
以下の流れで分析を進めていきます。
1. ライブラリのインストール
2. データの準備
3. 混合ガウスモデルによるクラスタリング
1. ライブラリのインストール
今回は機械学習ライブラリscikit-learnのGaussianMixtureを用いて混合ガウスモデルによるクラスタリングを行っていきます。
それ以外にも必要なライブラリをここでインストールしておきます。
#ライブラリのインストール
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.mixture import GaussianMixture2. データの準備
今回はirisと呼ばれる、アヤメの種類に関するデータセットを用いてクラスタリングを行っていきます。
一般的にirisデータセットは、4つの特徴量(花びら(petal)/がく片(sepal)それぞれの長さと幅(cm))を用いてアヤメの種類(3種類)を予測するという目的で使用されますが、今回は予測が目的ではないので特徴量の部分のみを使用します。
#データの準備
#irisデータセットをロード
iris = load_iris()
df = pd.DataFrame(data = iris.data, columns = iris.feature_names)
df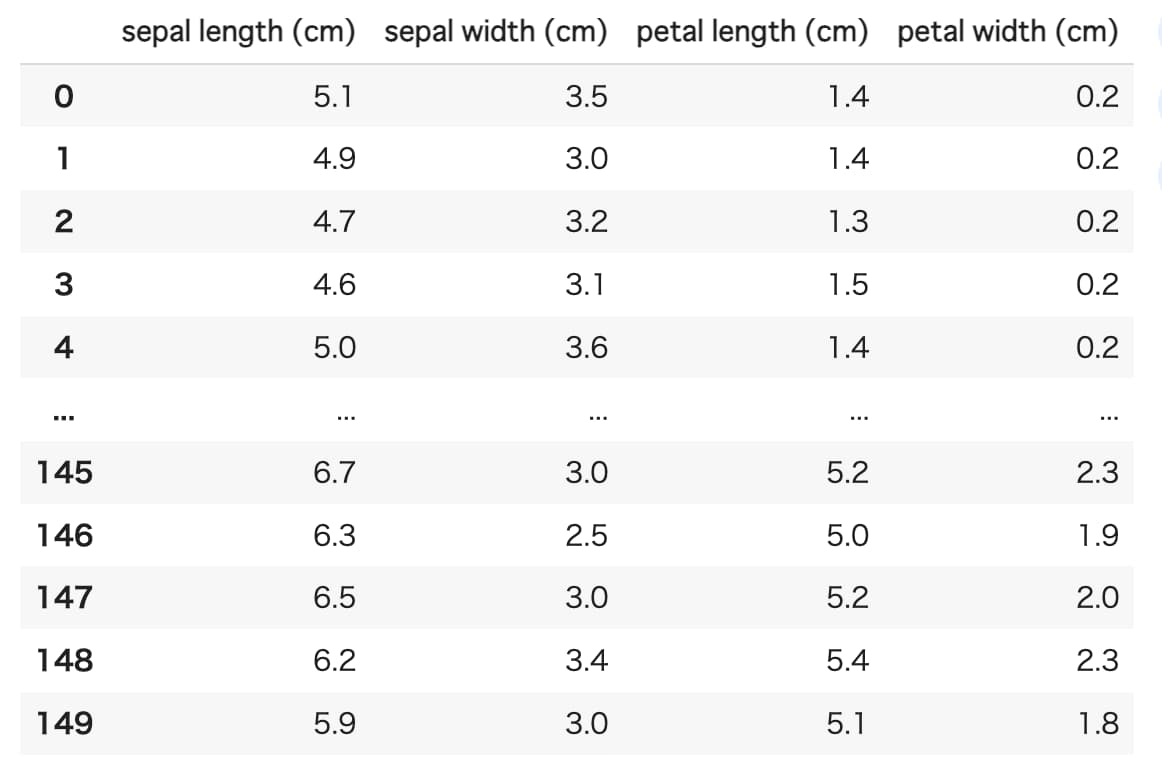
サンプルサイズは、1種類あたり50サンプル×3種類の計150となっています。
またここで、それぞれの変数の分布を確認してみましょう。
#グラフの表示
#4分割サブプロットを作成
fig, axs = plt.subplots(2, 2, figsize=(10, 8))
# サブプロットにデータをプロット
axs[0, 0].hist(df[iris.feature_names[0]], bins=20,density=True, alpha=0.5, color='b',edgecolor='black')
axs[0, 0].set_title(str(iris.feature_names[0]))
axs[0, 1].hist(df[iris.feature_names[1]], bins=20,density=True, alpha=0.5, color='r',edgecolor='black')
axs[0, 1].set_title(str(iris.feature_names[1]))
axs[1, 0].hist(df[iris.feature_names[2]], bins=20,density=True, alpha=0.5, color='g',edgecolor='black')
axs[1, 0].set_title(str(iris.feature_names[2]))
axs[1, 1].hist(df[iris.feature_names[3]], bins=20,density=True, alpha=0.5, color='y',edgecolor='black')
axs[1, 1].set_title(str(iris.feature_names[3]))
#レイアウトを調整
plt.tight_layout()
#グラフを表示
plt.show()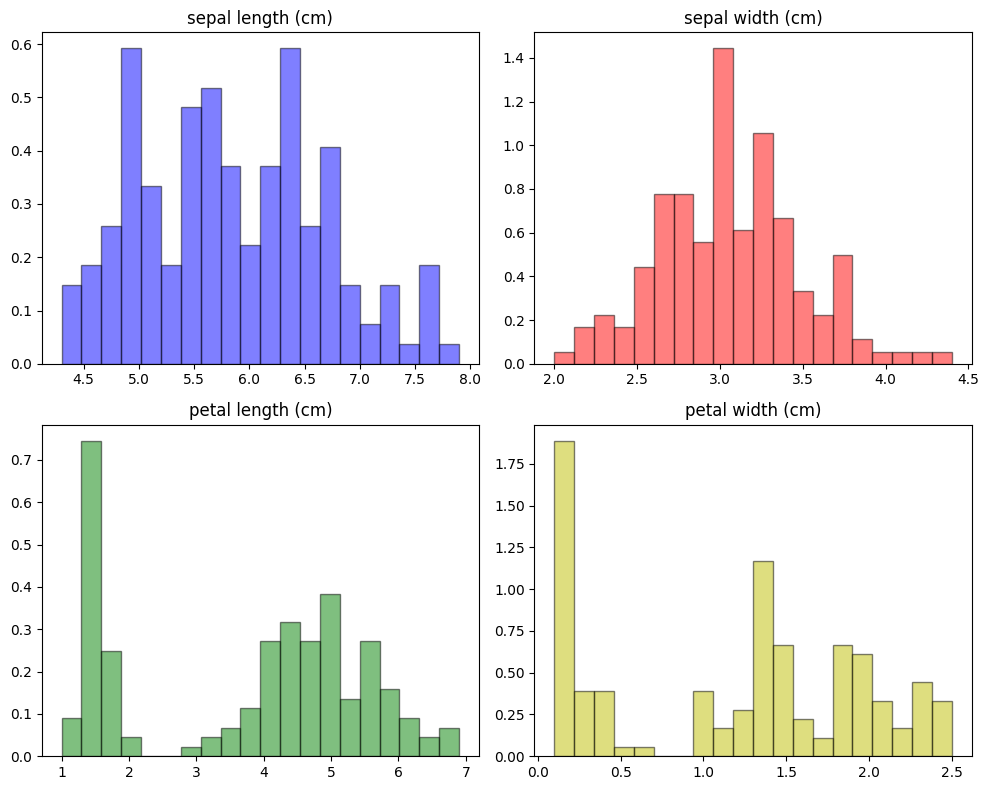
どの特徴量も複数の山ができており、単一のガウス分布ではなさそうであることが読み取れます。
3. 混合ガウスモデルによるクラスタリング
そして今回の目的である混合ガウスモデルによるクラスタリングを行っていきます。
あらかじめ想定されるクラスター数をリストに格納しておき、1から順番にGMM(Gaussian Mixture Model)を行ってBICを算出していく、という流れです。
そしてBICが最も小さくなった場合のクラスター数が最適クラスター数といえます。
#混合ガウスモデルによるクラスタリング
#データフレーム内のデータ(4次元)を特徴量とする
X = df.values
#想定するクラスター数のリスト
components_num = [1,2,3,4]
#クラスター数を1,2,...と振ってGMMを行い、BICを算出
for i in components_num:
gmm = GaussianMixture(n_components=i,covariance_type='full') #混合ガウスモデルを定義してフィット
gmm.fit(X)
BIC = gmm.bic(X) #BICの計算(GaussianMixtureのBICメソッドを用いる)
#クラスターを可視化(2次元で表示)
plt.scatter(X[:, 0], X[:, 1], c=gmm.predict(X), s=50)
plt.xlabel(str(iris.feature_names[0]))
plt.ylabel(str(iris.feature_names[1]))
#クラスタの中心をプロット
centers = gmm.means_
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, marker='X')
plt.title('The number of cluster : '+str(i)+' (BIC:'+str(round(BIC,1))+')')
#レイアウトを調整
plt.tight_layout()
plt.show()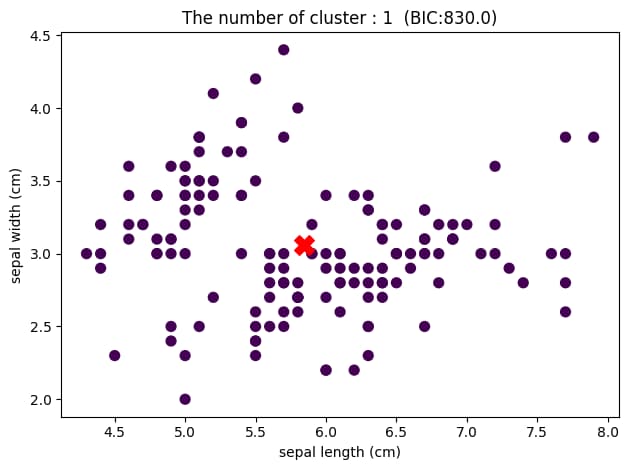
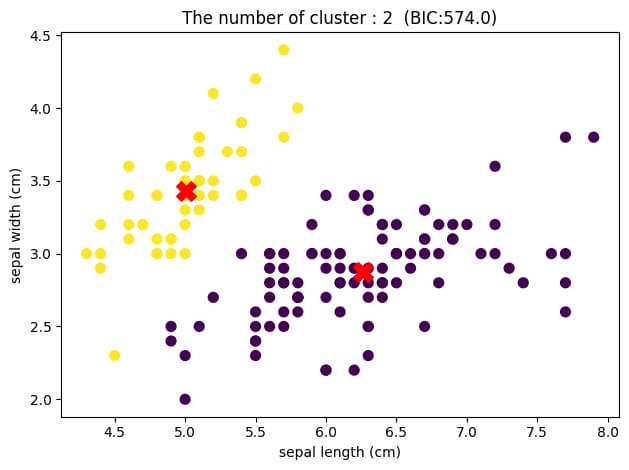
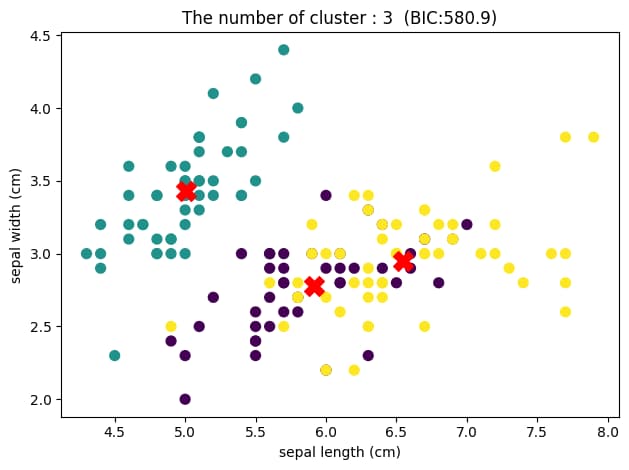
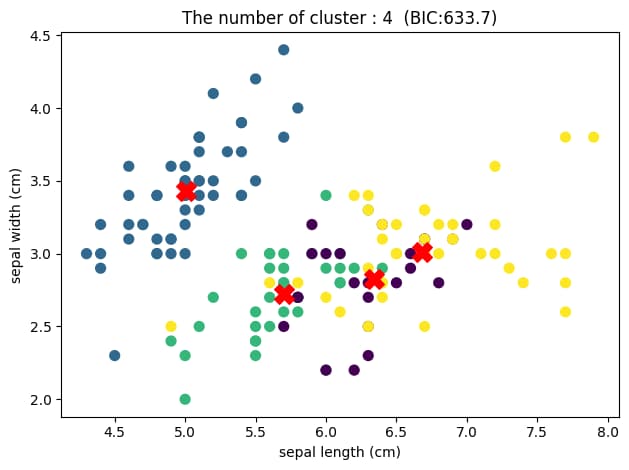
可視化のため2次元で表示していますが、クラスター数が2のときに最もBICが小さくなっていることがわかります。
つまり、このデータセットに対して混合ガウスモデルによるクラスタリングを行った結果、最適なクラスター数は2であり、上図のようなグループ分けがされたと結論づけることができます。
しかしここで、ある疑問が浮かび上がってくると思います。
それは、元々3種類のアヤメからなるデータセットであるにもかかわらずこのような結果が得られたのか、ということです。
その原因の一つとして、分布の重なりが大きい可能性が考えられます。
クラスター数が3の時の散布図を見てみると、緑色のグループは左上に固まっていますが、紫色と黄色のグループは重なり合っている部分が多いことがわかります。
これは、sepal widthとsepal lengthの2つの特徴量でデータを見たとき、紫色と黄色のデータをうまくグループ分けできていないことを表しています。
それにより、BICの値がクラスター数2のときよりも若干大きくなってしまっているのです。
そのため、混合ガウスモデルを用いてクラスタリングを行う場合、何かしらの事前情報があるのであればそれに基づいたクラスター数の設定を、そうでない場合はBICの値を基準とした自動的なクラスター数の設定を行っていきましょう。
まとめ
ここまでご覧いただきありがとうございました!
本記事では混合ガウスモデルの概要からPythonでの実装方法まで解説していきました。
混合ガウスモデルは単純な理論ながら、様々なデータに対して用いることのできる強力なクラスタリング手法です。
背後にガウス分布が想定できるデータであれば、ぜひ使っていきましょう!
また、今回分析に用いたPythonについて勉強したい方は以下の記事を参考にしてみてください!

さらに詳しくAIやデータサイエンスの勉強がしたい!という方は当サイト「スタビジ」が提供するスタビジアカデミーというサービスで体系的に学ぶことが可能ですので是非参考にしてみてください!
AIデータサイエンス特化スクール「スタアカ」

| 【価格】 | ライトプラン:1280円/月 プレミアムプラン:149,800円 |
|---|---|
| 【オススメ度】 | |
| 【サポート体制】 | |
| 【受講形式】 | オンライン形式 |
| 【学習範囲】 | データサイエンスを網羅的に学ぶ 実践的なビジネスフレームワークを学ぶ SQLとPythonを組み合わせて実データを使った様々なワークを行う マーケティングの実行プラン策定 マーケティングとデータ分析の掛け合わせで集客マネタイズ |
データサイエンティストとしての自分の経験をふまえてエッセンスを詰め込んだのがこちらのスタビジアカデミー、略して「スタアカ」!!
当メディアが運営するスクールです。
24時間以内の質問対応と現役データサイエンティストによる複数回のメンタリングを実施します!
カリキュラム自体は、他のスクールと比較して圧倒的に良い自信があるのでぜひ受講してみてください!
他のスクールのカリキュラムはPythonでの機械学習実装だけに焦点が当たっているものが多く、実務に即した内容になっていないものが多いです。
そんな課題感に対して、実務で使うことの多いSQLや機械学習のビジネス導入プロセスの理解なども合わせて学べるボリューム満点のコースになっています!
Pythonが初めての人でも学べるようなカリキュラムにしておりますので是非チェックしてみてください!
ウォルマートのデータを使って商品の予測分析をしたり、実務で使うことの多いGoogleプロダクトのBigQueryを使って投球分析をしたり、データサイエンティストに必要なビジネス・マーケティングの基礎を学んでマーケティングプランを作ってもらったり・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践してもらったりする盛りだくさんの内容になってます!
・BigQuery上でSQL、Google Colab上でPythonを使い野球の投球分析
・世界最大手小売企業のウォルマートの実データを用いた需要予測
・ビジネス・マーケティングの基礎を学んで実際の企業を題材にしたマーケティングプランの策定
・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践して稼ぐ























