変数が多い高次元データでは、通常の回帰分析が上手くいかない・そもそも解析不能なんてことが往々に起こります。
そんな高次元データの不都合を解決するのが「Lasso(ラッソ)回帰」や「Ridge(リッジ)回帰」！！
Lasso回帰・Ridge回帰は正則化やスパース推定と関連性が深いので、そちらを先にご覧いただけると理解が深まると思います。
この記事では、高次元データに対して効果を発揮する「Lasso(ラッソ)回帰」と「Ridge(リッジ)回帰」について見ていきましょう！
式や概念の説明だといまいちどんなことが起きているのかわからないので実際にR言語を用いて実装していきます！
目次
線形回帰・Lasso回帰・Ridge回帰とは
今回比較するのは、通常の線形回帰・Lasso回帰・Ridge回帰です。
簡単に、三つの手法について見ていきましょう！
通常の線形回帰
通常の線形回帰は残差\({\bf y}-{\bf X}{\bf \beta}\)が最小になるように\(\beta\)を推定します。
つまり、次の式を最小化するように\(\beta\)を推定します。
\begin{eqnarray*}
\|{\bf y}-{\bf X}{\bf \beta}\|_2^2\\
\end{eqnarray*}
Ridge回帰
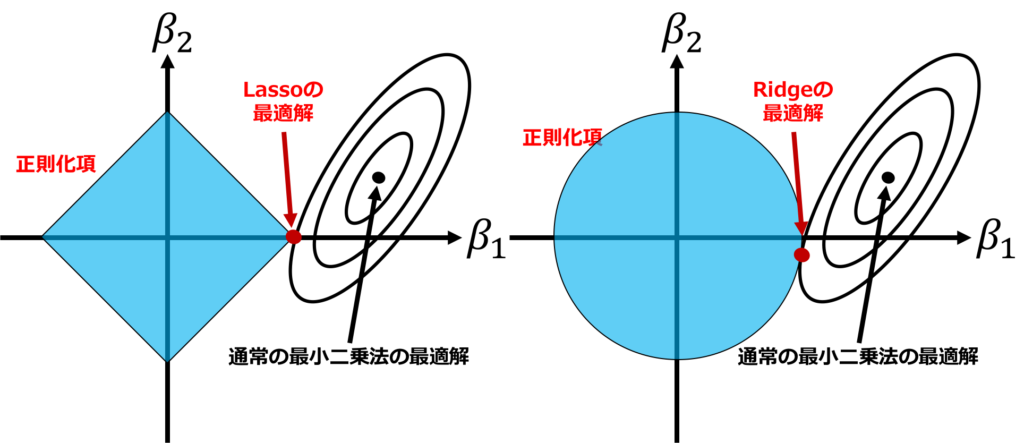
Ridge回帰は正則化手法であり、多重共線性などが起きていて通常の線形回帰ではパラメータが推定できないような場面でも罰則を与えることで推定できるようにしたものです。
次の式を最小化するように\(\beta\)を推定します。
\begin{eqnarray*}
\|{\bf y}-{\bf X}{\bf \beta}\|_2^2+\lambda\|{\bf \beta}\|_2^2\\
\end{eqnarray*}
第２項は正則化項と呼ばれ、なるべくパラメータ\(\beta\)の絶対値を小さくするような働きをします。
ここで、\(\lambda\)は正則化パラメータであり、解析者が設定するかクロスバリデーションなどで決定する必要があります。
詳しく知りたい場合、「Ridge回帰」の論文を見るとよいでしょう！
Proposed is an estimation procedure based on adding small positive quantities to the diagonal of X′X. Introduced is the ridge trace, a method for showing in two dimensions the effects of nonorthogonality.
引用：Google-“Ridge Regression: Biased Estimation for Nonorthogonal Problems”
Lasso回帰
Lasso回帰も正則化手法です。Ridge回帰とは異なりパラメータのいくつかを0に推定できるという特徴があります。
これをスパース推定と呼びます。次の式を最小化するように\(\beta\)を推定します。
\begin{eqnarray*}
\|{\bf y}-{\bf X}{\bf \beta}\|_2^2+\lambda\|{\bf \beta}\|_1\\
\end{eqnarray*}
今回は、線形回帰はglm()関数、LassoとRidgeはglmnetパッケージのglmnet()関数を用います。
詳しく知りたい場合、「Lasso回帰」の論文を見るとよいでしょう！
We propose a new method for estimation in linear models. the ‘lasso’ minimizes the residual sum of squares subject to the sum of the absolute value of the coefficients being less than a constant. Because of the nature of this constraint it tends to produce some coefficients that are exactly 0 and hence gives interpretable models.
引用：Google-“Regression Shrinkage and Selection via the Lasso”
Lasso回帰・Ridge回帰用の人工データ生成
データは、実データではなく自分で発生させる人工データを用います。
今回のデータの生成モデルを次に示します。
\begin{eqnarray*}
y_i&=&1+{\bf x}_i^T{\bf \beta}+\epsilon_i\\
{\bf \beta}&=&(1,0,-1,0,0)^T\\
{\bf x_i}&\sim& N({\bf \mu},{\bf \Sigma})\\
{\bf \mu}&=&{\bf 0}_5\\
{\bf \Sigma}&=&{\bf I}_5\\
\epsilon_i&\sim& N(0,1^2)\\
i&=&1,2,\cdots,n\\
\end{eqnarray*}
説明変数は、平均0・独立で発生させています。
また、\(\beta\)の設定から変数2・変数4・変数5は目的変数に寄与していません。
線形回帰・Lasso回帰・Ridge回帰をRで実装
先ほど説明したデータで解析をしてみましょう！
サンプルサイズ\(n\)は1100とします。
100個のデータを学習データ、残りの1000個のデータをテストデータとして実験します。
それぞれ３手法で推定された回帰係数と予測誤差(MSPE;Mean Squared Prediction Error)を計算してみましょう。
線形回帰・Lasso回帰・Ridge回帰の回帰係数
■通常の線形回帰で推定された回帰係数
(Intercept) 1.110727505
x1 0.862992782
x2 -0.024437489
x3 -0.757605621
x4 -0.098294387
x5 -0.008577822
■Lasso回帰で推定された回帰係数
(Intercept) 1.0713394
x1 0.7781268
x2 .
x3 -0.6778876
x4 .
x5 .
■Ridge回帰で推定された回帰係数
(Intercept) 1.08903319
x1 0.81095492
x2 -0.02288852
x3 -0.71278554
x4 -0.09335028
x5 -0.01748969
(Intercept)は定数項を表しています。
どうでしょうか、Lasso回帰は変数1と変数3以外は完全に0になっていることがわかります。
つまり、自動的に変数選択ができました！これは嬉しいですね！
回帰係数の2乗和を比較
また、推定された回帰係数の２乗和を計算すると次のようになりました。
■通常の線形回帰
> sum(as.matrix(result_glm$coefficients)^2)
2.562771
■Lasso
> sum(coefficients(result_lasso,s=”lambda.min”)^2)
2.212781
■Ridge
> sum(coefficients(result_ridge,s=”lambda.min”)^2)
2.361248
やはり、通常の線形回帰と比較して小さくなっています。
MSPEを比較
最後に、MSPEを比較します。
※MSPEは、Mean square prediction errorで予測値と観測値の差の二乗平均を取った値です。
■通常の線形回帰
> mean((data_test$y-yhat_glm)^2)
1.119285
■Lasso
> mean((data_test$y-yhat_lasso)^2)
1.171355
■Ridge
> mean((data_test$y-yhat_ridge)^2)
1.153019
最も良いのは通常の線形回帰になりました。
これはサンプルをたくさんあって、説明変数に相関もなく多重共線性が起きていないから当たり前ですね！
もっと、変数を増やしてみたりするとLassoやRidgeがMSPEで勝つこともあるでしょう。
ちなみに、このプログラムでは一回の計算なので結果の信頼性には欠けます。
そのため、続いてシミュレーションを何回か行って精度を検証していきましょう！
線形回帰・Lasso回帰・Ridge回帰の精度をシミュレーションで比較
どの手法が良いか・どのモデルが良いかを比較する為にはシミュレーションを繰り返して、指標の平均やばらつきをみて判断することが大切です。
たった一回の結果では本当に差があるのか偶然なのか信頼性に欠けるからです。
今回は線形回帰モデルの人工データを用いて線形回帰・Lasso・Ridgeの精度比較を行います。
実験の設定と手順
・比較手法：通常の線形回帰・Lasso回帰・Ridge回帰
・評価指標：MSPE(平均二乗予測誤差)
・シミュレーション回数：100回
実験の流れは簡単にこんな感じです。
- 人工データを生成
- データを解析
- 指標を算出して結果を格納
- 1~3を100回繰り返す
- 結果の平均とばらつきで比較
人工データ生成
今回のデータの生成モデルを次に示します。
\begin{eqnarray*}
y_i&=&1+{\bf x}_i^T{\bf \beta}+\epsilon_i\\
{\bf \beta}&=&(1,-1,0,\cdots,0)^T\in {\bf R}^p\\
{\bf x_i}&\sim& N({\bf \mu},{\bf \Sigma})\\
{\bf \mu}&=&{\bf 0}_p\\
{\bf \Sigma}&=&{\bf I}_p\\
\epsilon_i&\sim& N(0,1^2)\\
i&=&1,2,\cdots,n\\
\end{eqnarray*}
説明変数は\(p\)次元であり、平均0・独立で発生させています。
また、\(\beta\)はp次元ベクトルであり、変数1と変数2のみが目的変数へ寄与があります。
つまり、かなりスパースな設定になっています。
今回は、\(p\)を5,10,50と変化させて実験してみます。
シミュレーション実験
シミュレーション実験をしてみましょう。
サンプルサイズ\(n\)は1100とします。
100個のデータを学習データ、残りの1000個のデータをテストデータとして実験します。
今回用いるコード（\(p=50\)の場合）を載せておきます。
実行する前に入っていないパッケージはインストールしておいてください。
ばらつきも含めて見たいので結果を箱ひげ図で表します。
通常の線形回帰はglmと表記してあります。
・\(p=5\)の結果
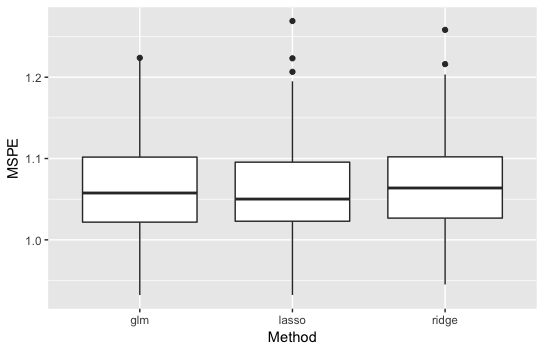
説明変数の数も多くないのであまり手法の差は見えません。
・\(p=10\)の結果
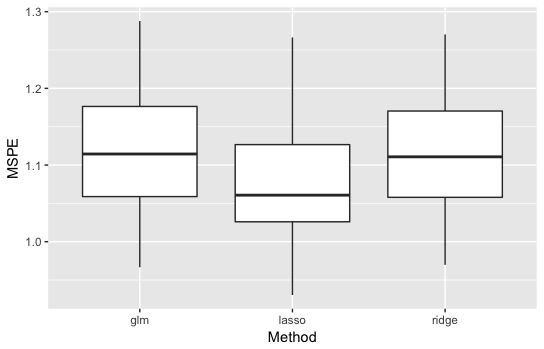
通常の線形回帰とRidgeは同じくらいですが、Lassoが良い精度を示しています。
説明変数が多くなってスパース性が上がったことが原因でしょう。
・\(p=50\)の結果
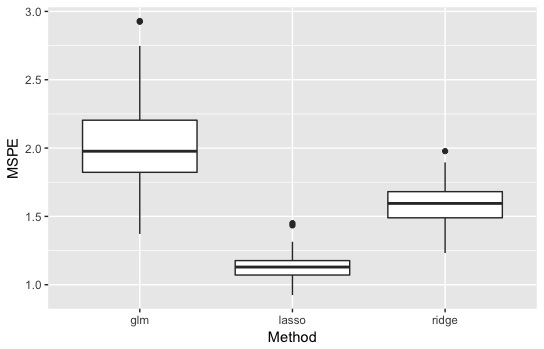
通常の線形回帰が最も悪くなり、Lassoが最も良くなりました。
差もかなり大きいです。
通常の線形回帰が悪い理由：サンプルサイズが100なのに対して説明変数が50次元なので推定が不安定になった。
Ridgeが２番目の理由：正則化しているので推定は安定しているがスパース性を考慮していないのでLassoより劣った。
よって、説明変数が多くて回帰係数がスパースのとき、Lassoは予測精度が通常の線形回帰・Ridgeと比べて良いことがわかりました。
こんな感じで手法の精度を比べたいときは、シミュレーションを繰り返して比較しましょう！
しかし、「今回は人工データだからたくさんデータを生成できるけど実データで精度比較したいときはどうするの？」という疑問が出てくると思います。その場合には交差検証法を使って比較します。
Ridge・Lassoについて理論から知りたい方はこちらの記事をご覧ください！
また、機械学習手法やデータサイエンスの広範な範囲について知りたい方はぜひ以下の記事をチェックしてみてくださいね！
さらに当メディアでは機械学習やデータサイエンスについて幅広く学べるスクール「スタアカ」を展開しています！
ぜひチェックしてみてください！
スタビジのコンテンツをさらに深堀りしたコンテンツが動画と一緒に学べるスクールです。
プレミアムプランでは私がマンツーマンで伴走させていただきます！ご受講お待ちしております！
