ホテリング管理図

この記事では、管理図の原点であり、今では様々な手法の土台となっているホテリング管理図について見ていきたいと思います。

ホテリング管理図とは

ホテリング管理図とは、1947年にHottelingが考案した多変量異常検知の手法です！

多変量管理図を理解する上で一番はじめに理解するべき全ての基礎となる手法です。

ホテリング管理図では、マハラノビス距離を用いて異常検知を行います。

マハラノビス距離とは変数の相関関係を考慮した上で距離を算出します。

相関関係は考慮しない純粋な距離はユークリッド距離と呼ばれ馴染みが深いですね！

では、マハラノビス距離とは具体的にどのような距離なのでしょうか？

マハラノビス距離とは

マハラノビスとは相関関係を考慮した距離！

体重と身長の２変数で考えてみましょう！

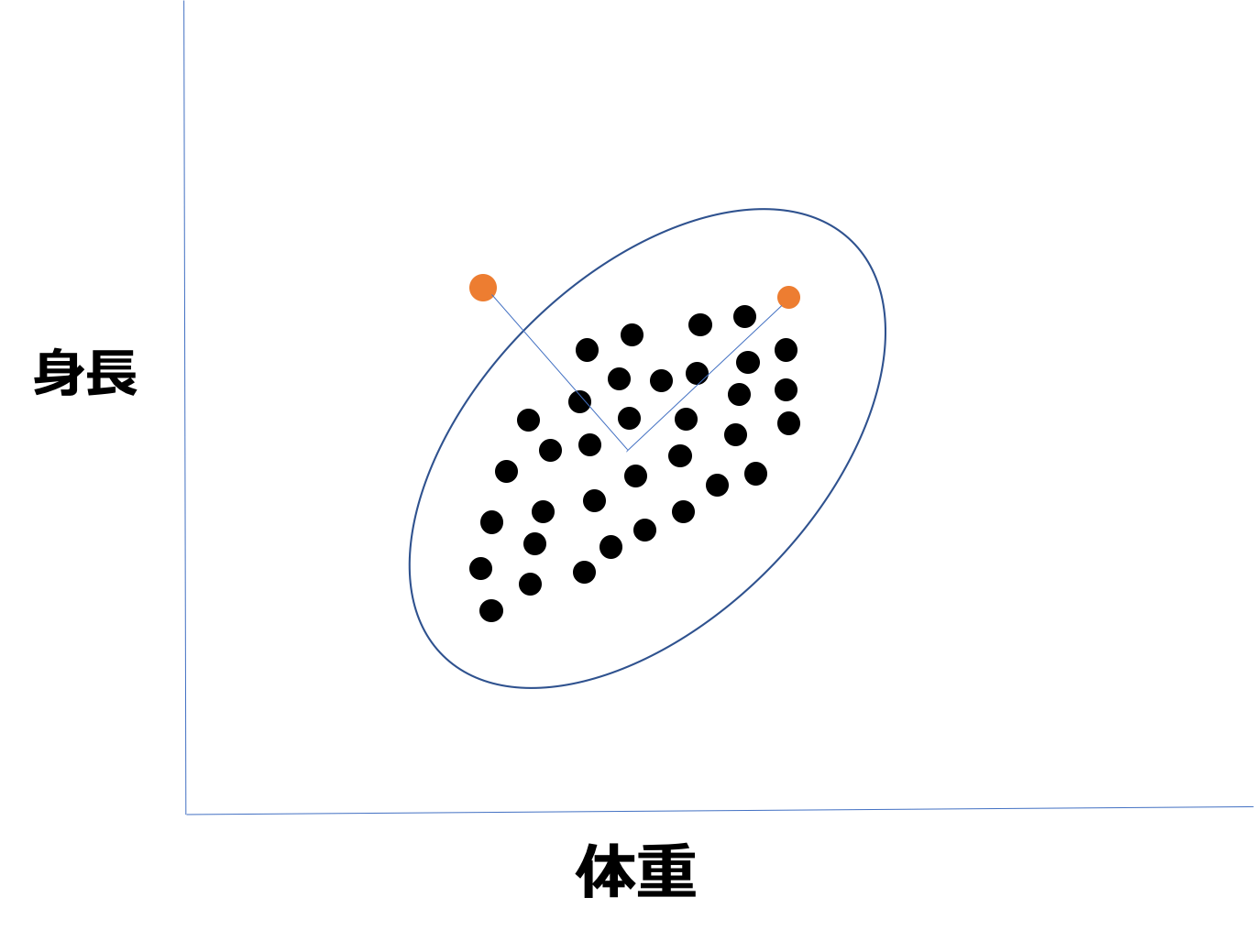
身長を縦軸に体重を横軸に取りましょう。

この時、オレンジの点が2つありますよね。どちらが異常でしょうか？

視覚的に見るとあきらかに左の点ですね。ただ、この2つの点は全体の中心点からのユークリッド距離は一緒なのです。

すなわちユークリッド距離で異常を判断するのは妥当ではない！！ということがわかりますね！

そこで相関関係を考慮したマハラノビス距離の登場です！

具体的には変数の分散共分散行列の逆行列を変数ベクトルに掛けあわせて算出しますよ！

具体的な手順

MT法による解析の手順は以下の通りです。

1. 正常と分かっているp次元のデータ\({\bf x}_i,(i=1,2,\cdots,n)\)から標本平均ベクトル\(\hat{\mu}\)と標本共分散行列\(\hat{{\bf \Sigma}}\)を計算します。
   \begin{eqnarray*}
   \hat{\mu}&=&\frac{1}{n}\sum_{i=1}^n{\bf x}_i\\
   \hat{{\bf \Sigma}}&=&\frac{1}{n}\sum_{i=1}^n({\bf x}_i-\hat{\mu})({\bf x}_i-\hat{\mu})^{T}\\
   \end{eqnarray*}
2. 判別したいデータ\({{\bf x}’}\)の異常スコア\(d({{\bf x}’})\)を計算します。
   \begin{eqnarray*}
   d({{\bf x}’})&=&({{\bf x}’}-\hat{\mu})^{T}{\bf \hat{\Sigma}}^{-1}({{\bf x}’}-\hat{\mu})\\
   \hat{{\bf \Sigma}}&=&\frac{1}{n}\sum_{i=1}^n({\bf x}_i-\hat{\mu})({\bf x}_i-\hat{\mu})^{T}\\
   \end{eqnarray*}
3. \(d({{\bf x}’})\)がある閾値より小さければ正常、大きければ異常と判別します。

実はこのホテリング管理図の考え方に対して、異常に寄与している変数を見つけ出すSN比という指標を取り入れたのが田口玄一先生が考案したMT法です。

そちらもあわせて学習されるとより理解が深まるでしょう！

ホテリング管理図　まとめ

ホテリング管理図は非常に古い手法ですが、これを基に様々な発展的な手法が生み出されています。

他の管理図については以下の記事をご覧ください！

管理図とは当サイト【スタビジ】の本記事では、品質管理の分野でよく使われる管理図について徹底的に見ていきます。単変量管理図と多変量管理図の2タイプがあり、多変量管理図は研究も盛んでまだまだこれから新しい手法が登場するでしょう！...