ベイズ統計学は最近になって脚光を浴びるようになってきた新たな手法。
伝統的な統計学とは一線を画す考え方だったのですが、現在は切っても切り離せない存在となってきています。
この記事では、統計学を勉強する上で非常に重要な分野であるベイズ統計学について説明していきます。
ベイズは高校生の確率の教科書などにも載っている、ベイズの定理を基本の原則として、様々な方面へ応用できます。
ここでは大きな枠組みを捉えるということで、
・ベイズ統計学とは
・ベイズの定理
・ベイズ推定
・MCMC（マルコフ連鎖モンテカルロ法）
・プログラミング言語（Stan/WinBugs）
・オススメ勉強法
の順番で解説していきますよ！
以下の動画でも簡単に解説していますので、こちらも参考にしてみてください！
目次
ベイズ統計学ってなに？
ベイズ統計学は非常に奥が深く面白い分野なんです！
ベイズ統計の定理
ベイズの定理はベイズ統計学の基本中の基本。大事な式なので覚えておきましょう。
\begin{eqnarray*}
p(A|B)&=&\frac{p(B|A)p(A)}{p(B)}
\end{eqnarray*}
これは以下の条件付き確率と同時確率の関係から導出できます。
\begin{eqnarray*}
p(A,B)=p(B|A)p(A)=p(A|B)p(B)
\end{eqnarray*}
この関係式を変形するとベイズの定理が導出されることが分かるでしょう。
ある町で１００人に１人かかる病気Aがある。
病気Aにかかった人が検査Bを受けると９割が陽性と判定される。
健康な人が検査Bを受けると9.5割が陰性と判定される。
陽性と判定された時、病気Aにかかっている可能性はどのくらいか。
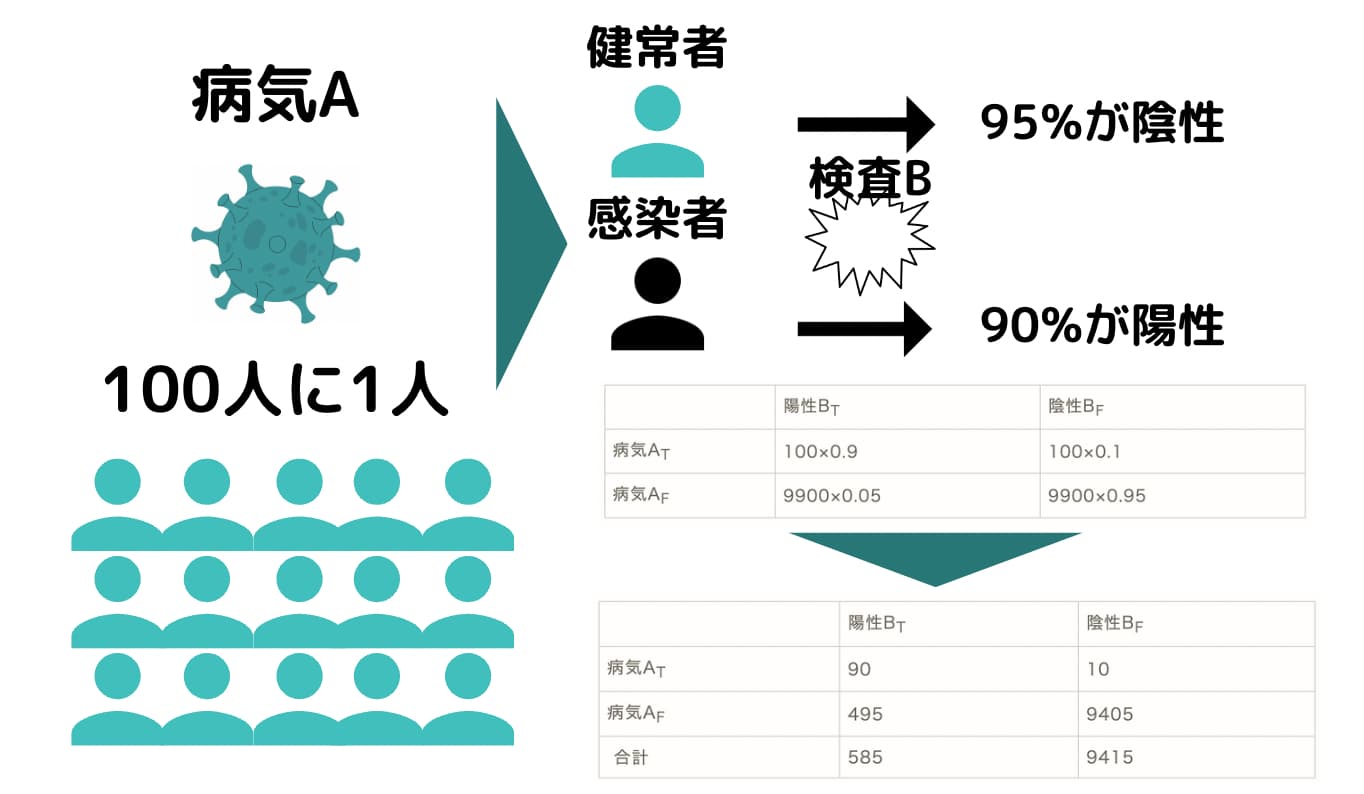
まずは、ベイズの定理は使わず実際の数値をあてはめて考えていきましょう！
この町に10000人いると考えてみましょう！
| 陽性BT | 陰性BF | |
| 病気AT | 100×0.9 | 100×0.1 |
| 病気AF | 9900×0.05 | 9900×0.95 |
| 陽性BT | 陰性BF | |
| 病気AT | 90 | 10 |
| 病気AF | 495 | 9405 |
| 合計 | 585 | 9415 |
実際に数値を当てはめても算出することができますが、ベイズの定理を用いることでこの数値を算出することができます。
おさらいですが、ベイズの定理は以下のように表すことが出来ました。
\begin{eqnarray*}
p(A|B)&=&\frac{p(B|A)p(A)}{p(B)}
\end{eqnarray*}
この時、今回のケースでは以下のようになっていますね。
A：病気である事象
B：陽性と判定される事象
求めたいのは、
P(A|B)：陽性と判定された時に本当に病気にかかっている確率
ベイズの定理を使えば、P(A|B)を求めるのにP(A)・P(B)・P(B|A)の情報さえ分かればよさそうですね。
この時、
P(A)：病気にかかっている確率 ＝ 0.01
P(B|A)：病気にかかっている時に陽性と判定される確率 ＝ 0.9
P(B)：陽性と判定される確率 =？？
P(B)は確率の分解をして求めていきます。
\begin{eqnarray*}
p(B)&=&p(B|A_T)p(A_T)+p(B|A_F)p(A_F)=0.9×0.01+0.05×0.99=0.0585
\end{eqnarray*}
ということは・・・
\begin{eqnarray*}
p(A|B)&=&\frac{p(B|A)p(A)}{p(B)}=0.01*0.9/0.0585=0.15384615384
\end{eqnarray*}
となります！
さっきの15.4％と一致しましたね！
さらにベイズの定理の面白さを知るのにおすすめなのがモンティ・ホール問題という問題。
モンティ・ホール問題は以下のような問題です。
あなたの前に閉じた3つのドアABCがあって、1つのドアの後ろには当たりが、2つのドアの後ろにははずれがある。
あなたが1つのドアを選択した後、司会が残りのドアのうちはずれのドアを開けてあなたに見せる。
ここであなたは、最初に選んだドアを、残っている開けられていないドアに変更してもよいと言われる。
あなたは変更するべきか？変更しないべきか？
この時、実はドアを変更したほうが当たる確率が2倍になるのです！
以下の記事でベイズの定理からモンティ・ホール問題について解説しているので是非チェックしてみてください！
ベイズ推定
先ほどのベイズの定理や例題では基本的に確率を元に考えていました。
しかし、ベイズの枠組みはそれだけではおさまりません。
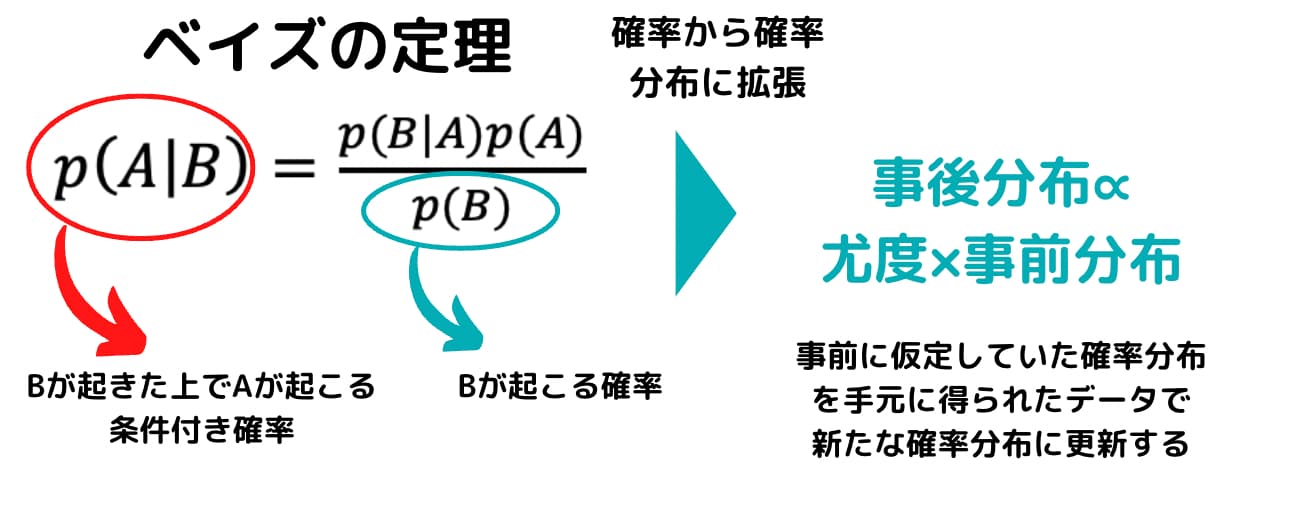
このベイズ推定では、ベイズの定理における確率を確率分布へと拡張させ考えていきます。
ベイズ推定に関しては事前分布と事後分布、そして尤度という考え方が非常に重要です。
事前分布は前から持っている情報。尤度は手に入れた情報。
事後分布は前情報と手に入れた情報を合わせた情報というイメージを持っていれば良いでしょう。
\begin{eqnarray*}
p(A|B){\propto}p(B|A)p(A)
＝事後分布{\propto}尤度×事前分布
\end{eqnarray*}
表の出る確率が0.5のコインが一般的なイメージですが、もしかしたら0.3かもしれないしはたまた0.7かもしれません。
本当のところは分かりません。
ベイズ統計学では、パラメータ（表の出る確率）が何なのかを確率分布で表します。
事前にある程度の情報がある時は、その情報を基にして事前分布を定義します。
一方で事前分布にどんな分布を設定したらよいか分からない時はどうすればよいでしょう？
ベイズでは事前情報の全くない状態を無情報事前分布と言い、一般的には一様分布を用いることが多いです。
実際に起きた事象を基に確率分布を更新していき、パラメータ（表の出る確率）の事後分布を算出するのがベイズ推定なのです。
MCMC（マルコフ連鎖モンテカルロ法）
さっきも出てきましたが、ベイズ統計学の最近の台頭の立役者です。
MCMCがなかったら正直ベイズ統計学はここまで盛り上がっていないはずです。
では、MCMCとは何なのでしょうか？
そうなんです。実はMCMCは非常に簡単な方法で、基本的には以下のようなアルゴリズムです。
１．あるパラメータの尤度を計算する
２．そこからパラメータを上下に動かし尤度を計算し、よくなった方に動く。
３．定常状態になるまでパラメータを動かす。
ベイズ統計で使うプログラミング言語
続いてベイズを勉強するためのプログラミング言語に関してです。
ベイズのアルゴリズムは基本的にどんなプログラミング言語でも記述することができますが、より容易に記述するための言語が実装されています。
例えば、StanやWinBugsなどです。
どちらも使ったことがありますが、現環境だと圧倒的にStanの方がオススメです。
Stanは記述に癖がなく、RやPythonで回すことができます。エラーも分かりやすいため初心者にはStanをおすすめします。
StanをRで実装するなら
Stan×Rを勉強するなら以下の本が圧倒的にオススメ！
■StanとRでベイズ統計モデリング
Stanを勉強する上でのオススメ本は以下にまとめています！
StanをPythonで実装するなら
Stan×Pythonなら以下のUdemy講座が圧倒的におすすめ！
この教材では、ベイズの基本的な概念からMCMC・階層ベイズ・状態空間モデルをPythonとStanを使いながら実装していきます。
理論と実装が分かりやすく学べるので非常におすすめなんです！
なかなかStanが学べる教材はないので貴重です。
ぜひチェックしてみてくださいねー！
ベイズ統計学 まとめ
ベイズ統計学について簡単にまとめてきました。
実はベイズ統計学は非常に奥が深くて色んな考え方があるんです！
ベイズを勉強するとは言っても色んな書籍があってなかなかどれが良いか分からないと思います。
以下の書籍が特にオススメなので是非読んでみて下さい。
■データ解析のための統計モデリング入門
回帰モデルからベイズモデルまでの流れがスムーズに分かります。
以下の記事にベイズ統計学のオススメ本をまとめているのであわせてご覧ください！
イラスト出典：Illustration by Stories by Freepik
スタビジのコンテンツをさらに深堀りしたコンテンツが動画と一緒に学べるスクールです。
プレミアムプランでは私がマンツーマンで伴走させていただきます！ご受講お待ちしております！
