こんにちは！スタビジ編集部です！
機械学習の分野において広く利用されているシグモイド関数。
「聞いたことはあるけど、細かい数式とかはわからない！」という方も多いのではないでしょうか。
本記事では、そんな方に向けて、シグモイド関数の概要からPythonによる実装方法までをわかりやすく解説していきます！
シグモイド関数とは？
シグモイド関数とは、下記の数式で表される関数です。
\(\displaystyle f(x) = \frac{1}{1+e^{-x}}\)
図示するとこのようなグラフを描くことができます。
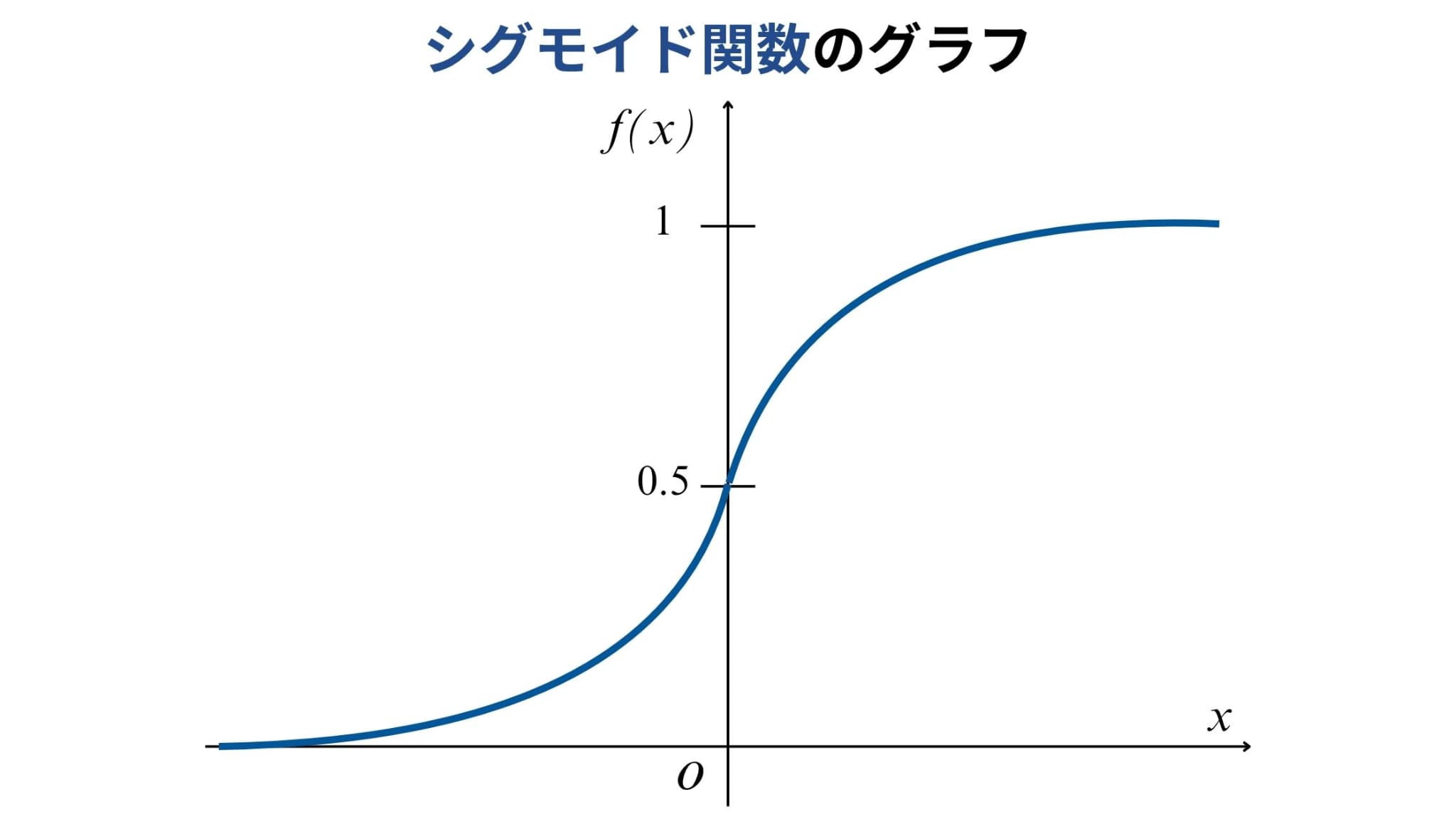
数式や図を見るとわかるように、どんな入力値\(x\)に対しても0〜1の出力が返されることが特徴です。
このことから、シグモイド関数の出力は確率のように解釈することができます。
具体例を用いて説明していきます。
例えば、「ある患者がA病という病気にかかっているかどうか」を判定する場合を考えてみましょう。
その患者に対して血液検査などを行った結果、1.4というスコアが算出されたとします（スコアの算出方法は独自で決まっているものとします）。
その値をシグモイド関数の入力\(x\)として渡すと、
\(\displaystyle f(1.4) = \frac{1}{1+e^{-1.4}} ≒ 0.8\)
となり、出力は約0.8となります。
つまり、この0.8はその患者がA病にかかっている確率（=80%）と解釈することができるのです。
なお、病気にかかっているかどうか判定する場合は、閾値をあらかじめ設定しておくことが必要です（閾値を50%と設定した場合、50%以上であれば病気であると判定）。
この考えを応用したのがロジスティック回帰であり、上記のようなデータを学習することで、患者がA病であるかどうかを予測するモデルを作成することができます。
ソフトマックス関数との違い
シグモイド関数と似た関数に、ソフトマックス関数があります。
\(\displaystyle φ(u_i) = \frac{e^{u_i}}{\sum_{k=1}^{N} e^{u_k}}\)
どちらも出力が0〜1となる関数ですが、ソフトマックス関数は複数の入力に対して複数の出力を返す、シグモイド関数は一つの入力に対して一つの出力を返すという違いがあります。
この性質から、シグモイド関数は二値分類に、ソフトマックス関数は多値分類に利用されています。
ソフトマックス関数については以下の記事で詳しく解説しています！
シグモイド関数の利用場面
ここまでシグモイド関数について解説してきましたが、実際にはどのような場面で利用されているのでしょうか。
1. ロジスティック回帰
一番有名なのは、概要部分でも触れたロジスティック回帰でしょう。
\(\displaystyle y = \frac{1}{1+e^{-z}}\)
モデル自体がシグモイド関数の形をしており、入力\(z\)の部分が、下記のような重回帰モデルの形となっています。
\(\displaystyle z = a_{1}x_{1} + a_{2}x_{2} + … +a_{n}x_{n} + b\)
二値分類のためのモデルとして、様々な分野で活用されています。
2. 活性化関数
シグモイド関数は、ニューラルネットワークの活性化関数として利用されることがあります。
シグモイド関数が活性化関数として利用されるのは微分可能であることが主な理由です。
微分可能であることにより、ニューラルネットワークにおける誤差逆伝播法で活用することができます。
誤差逆伝播法については以下の記事で詳しく解説しています！
シグモイド関数をPythonで実装
それでは実際にシグモイド関数をPythonで実装していきましょう！
下記コードでは、冒頭で示した数式を定義し、matplotlibを使ってグラフを表示しています。
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
# シグモイド関数
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# xの範囲を設定
x = np.linspace(-10, 10, 200) # -10 から 10
y = sigmoid(x)
# グラフ描画
plt.figure(figsize=(6, 4))
plt.plot(x, y, label="f(x)", color="blue")
# 補助線
plt.axhline(0, color="black", linewidth=0.5, linestyle="--")
plt.axhline(1, color="black", linewidth=0.5, linestyle="--")
plt.axvline(0, color="black", linewidth=0.5, linestyle="--")
# タイトル等
plt.title("シグモイド関数")
plt.xlabel("x")
plt.ylabel("f(x)")
plt.legend()
plt.grid(True)
plt.show()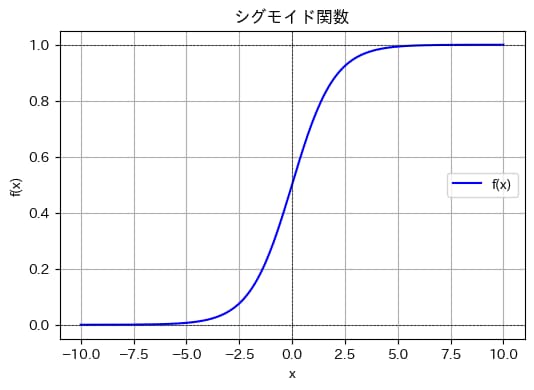
きちんと\(f(x)\)の範囲が0〜1に収まっていることがわかりますね！
まとめ
ここまで、シグモイド関数の概要とPythonでの実装方法について解説してきました。
冒頭でも述べたように、シグモイド関数は様々な分野で広く利用されている関数です。
本記事で得た知識をもとに、ぜひ実務でも活用してみましょう！
さらに詳しくAIやデータサイエンスの勉強がしたい！という方は当サイト「スタビジ」が提供するスタビジアカデミーというサービスで体系的に学ぶことが可能ですので是非参考にしてみてください！
AIデータサイエンス特化スクール「スタアカ」
| 【価格】 | ライトプラン：1280円/月 プレミアムプラン：149,800円 |
|---|---|
| 【オススメ度】 | |
| 【サポート体制】 | |
| 【受講形式】 | オンライン形式 |
| 【学習範囲】 | データサイエンスを網羅的に学ぶ 実践的なビジネスフレームワークを学ぶ SQLとPythonを組み合わせて実データを使った様々なワークを行う マーケティングの実行プラン策定 マーケティングとデータ分析の掛け合わせで集客マネタイズ |
データサイエンティストとしての自分の経験をふまえてエッセンスを詰め込んだのがこちらのスタビジアカデミー、略して「スタアカ」！！
当メディアが運営するスクールです。
24時間以内の質問対応と現役データサイエンティストによる複数回のメンタリングを実施します！
カリキュラム自体は、他のスクールと比較して圧倒的に良い自信があるのでぜひ受講してみてください！
他のスクールのカリキュラムはPythonでの機械学習実装だけに焦点が当たっているものが多く、実務に即した内容になっていないものが多いです。
そんな課題感に対して、実務で使うことの多いSQLや機械学習のビジネス導入プロセスの理解なども合わせて学べるボリューム満点のコースになっています！
Pythonが初めての人でも学べるようなカリキュラムにしておりますので是非チェックしてみてください！
ウォルマートのデータを使って商品の予測分析をしたり、実務で使うことの多いGoogleプロダクトのBigQueryを使って投球分析をしたり、データサイエンティストに必要なビジネス・マーケティングの基礎を学んでマーケティングプランを作ってもらったり・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践してもらったりする盛りだくさんの内容になってます！
・BigQuery上でSQL、Google Colab上でPythonを使い野球の投球分析
・世界最大手小売企業のウォルマートの実データを用いた需要予測
・ビジネス・マーケティングの基礎を学んで実際の企業を題材にしたマーケティングプランの策定
・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践して稼ぐ
スタビジのコンテンツをさらに深堀りしたコンテンツが動画と一緒に学べるスクールです。
プレミアムプランでは私がマンツーマンで伴走させていただきます！ご受講お待ちしております！
