Box-cox変換を用いて正規分布に従わないデータを解析してみよう！

こんにちは！

あるデータに対して線形回帰分析（一般的に用いられる重回帰分析）を行ってみたけど上手くいかない・・・

そんなことよくありますよね！

なんでも線形回帰分析を適応していいわけではないんです。

この記事では、実際にデータによってはどのような問題が発生してしまうのか、どのように解決していけばよいのか見ていきましょう！

以下のYoutube動画でも詳しく解説しています！

どんな問題があるの？

一般的に良く用いられる線形回帰分析というのは、データが正規分布に従うという仮定を置いているんですね！

※厳密には残差が正規分布に従う

正規分布というのはこんな分布！

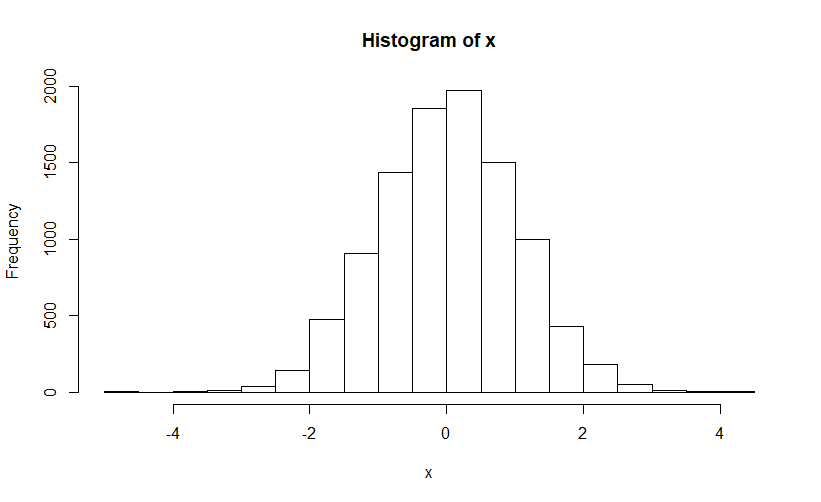
統計学で最も良く出てくる分布ですね！

データの分布がこのようになっていないと上手く線形回帰分析が当てはまらないんです！

でも実際世の中のデータはこんなきれいな正規分布に従っていないものばかり！

Box-Cox変換で解決！

それでは、どうすればよいのでしょうか？

このようにデータの従う分布が決められているような線形回帰分析などの手法をパラメトリックモデルと呼びます。

これに対して、最近流行りの機械学習手法はノンパラメトリックモデルと呼ばれ、背後に分布を想定していないものが多いです。

だからランダムフォレストやサポートベクター回帰などのノンパラメトリックモデル手法を使って解析することは一つの手でしょう！

ただ、やはりデータの構造が分かるならそれに沿った解析を行いたいし、パラメトリックモデルの方が解析結果の解釈が容易です。

そこで大きく分けて二つの方法が存在します。

一つは、正規分布でない分布を背後に仮定した回帰手法を用いること。

ポアソン回帰などがその例ですね。

あとはそれらの回帰分析を混合した一般化線形混合モデルなども存在します。

これらに関しては、以下の記事で詳しく取り上げておりますので良かったら見てみてください！

https://toukei-lab.com/%E7%B5%B1%E8%A8%88%E3%83%A2%E3%83%87%E3%83%AB

そして二つ目は、データの構造を無理やり正規分布に変換しちゃうというもの！

Box-Cox変換と呼びます。

定義は以下の通りです。

\begin{eqnarray}
{y}^\lambda
=
\begin{cases}
\frac{ {y}^\lambda-1 }{ \lambda } & ( \lambda \neq 0 ) \\
log{(y_i)} & ( \lambda = 0 )
\end{cases}
\end{eqnarray}

でもこのBox-cox変換はなんでもかんでも変換しちゃえば良いというものではなくて説明変数がある程度正規分布に従わないと目的変数を正規変換してもあまり意味ないんです。

また、Box-cox変換の弱点は定義をみれば分かると思いますが、負の値は変換できないということ。

これを改善してくれたのがYeo-Johnson変換です。

定義は以下の通り。

\begin{eqnarray}
{y}^\lambda
=
\begin{cases}
\frac{{y+1}^\lambda-1}{\lambda} & ( \lambda \neq 0 , y\geq0) \\
log{(y+1)} & ( \lambda = 0 , y\geq0)\\
\frac{-[(-y+1)^{2-\lambda}-1]}{(2-\lambda)}& ( \lambda \neq 2 , y\lt0)\\
-log{(-y+1)} & ( \lambda = 2 , y\lt0)\\
\end{cases}
\end{eqnarray}

複雑そうに見えますが、そんなこともないですよー！

でもあんまり使わないかなーという印象です。

ちなみにBox-cox変換は、Rで簡単に実装できます。最適な$\lambda$もRで一発で求めることができちゃうんです！

具体的には、carパッケージのpowerTransformという関数を用いて、$\lambda$を推定し、bcPower関数で変換を行います。

Yeo-Johnson変換もパッケージありますが、ここでは取り上げません。

それでは、実際に実データを用いて解析を行ってみましょう！

Box-Cox変換を用いて実データ解析

今回用いるデータは北京における大気汚染PM2.5です。

中国における大気汚染の問題は日に日に深刻になっていますが、過去のデータから将来のPM2.5の値は予測することができるのでしょうか？

解析するデータの構造は以下の通り。

このデータでは、PM2.5の濃度を目的変数、年を除いた他の10の変数を説明変数として解析を行います。

先ほども申し上げましたが、解析の目的としては現状観測されているPM2.5の濃度から将来のPM2.5を予測するというもの。

サンプルは、2010年1月1日～2014年12月31日まで存在し、1時間ごとに測定されています。

2010年1月1日～2013年12月31日の4年間のデータから2014年1月1日～2014年12月31日までの各時間のpm2.5の濃度を予測します。

まず、データを取り込み、学習データと予測データに分けます。

その後回帰分析を行い、予測値と観測値の差を計算します。

ここで用いる評価指標はRMSEと呼ばれるもので、予測値と観測値の差の二乗和の平均に平方根をとったものです。

予測精度の評価指標としてよく用いられます。

library(dplyr)
library(car)

data<-read.csv("Beijing_PM2.5.csv")
data2<-data%>%filter(pm2.5!="NA")#欠損値削除
data2<-data2[,-1]
data.train<-data2%>%filter(year!="2014")#学習データ作成
data.test<-data2%>%filter(year=="2014")#テストデータ作成

#スタンダードな回帰
result<-lm(pm2.5~.,data=data.train[,-1])#回帰モデル作成
pre<-predict(result,data.test)#予測値
rmse1<-sqrt(mean((data.test$pm2.5-pre)^2))#RMSEを計算

RMSEの値は81.098となりました。

うーん、PM2.5に関して詳しく見てみると、最小の値が0で、最大の値が994、標準偏差が92であるため、相当ばらつきの大きいデータとなっていることがわかります。

ここで、ヒストグラムを描いてみると以下のようになります。

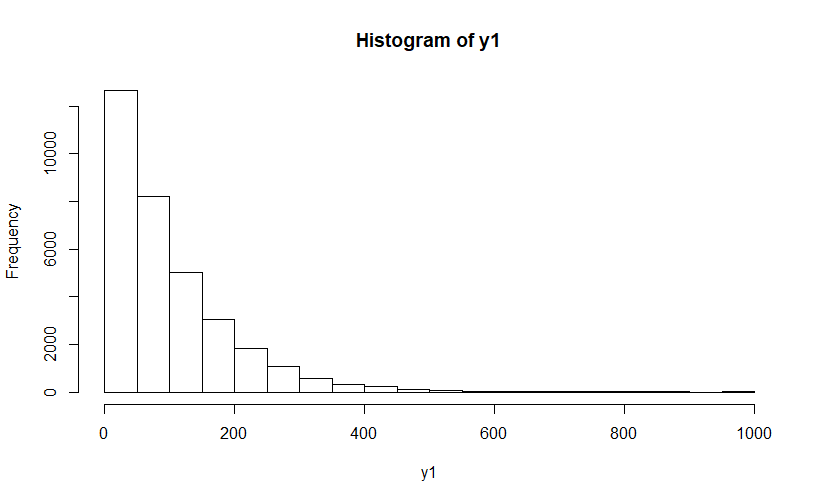
全く正規分布になっていませんね！カイ二乗分布に近いようです。

ここで、Box-cox変換の出番！！変換を施し再度計算してみましょう！

#Box-cox変換を施した回帰
y1=(data.train$pm2.5+0.1)#0を無くすためのの補正
p1<-powerTransform(y1)
data.train[,5]<-bcPower(y1,p1$lambda)
result<-lm(pm2.5~.,data=data.train[,-1])#回帰モデル作成
pre<-predict(result,data.test)#予測値
pre2<-((pre*p1$lambda)+1)^(1/p1$lambda)
rmse2<-sqrt(mean(data.test$pm2.5-pre2)^2)#RMSEを計算

この時、RのpowerTransformだと0の値に対して計算をしてくれないので、0.1をプラスして補正をかけてます。

そんで最終的には定義に従って逆変換を施してます！

この逆変換に関しては、パッケージはないので自分で定義から定式化してみましょう！

実際にRMSEを計算してみると23.03になりました！大幅な改善！

ぶっちゃけ他の機械学習手法使った方が予測精度的には良くなるかもしれませんが、アルゴリズムわからずとりあえず使うよりも、データの構造を把握した上で基本的な手法を用いたほうが解釈容易性も高く、相手に伝えやすかったりします！

時と場合によって使いわけましょう！

Box-cox変換　まとめ

ここまでご覧いただきありがとうございました！

Box-cox変換を使ってこんなことができるよ！というお話でした！

Box-cox変換を行わずに単純なLog変換でも問題ないこともあります。

データの構造に偏りが見られたときは変換してみましょう！

よりさらに深く統計学や機械学習を学びたい人のために勉強法を以下にまとめていますのでぜひチェックしてみてください！

【初心者必見】統計学入門に必要な知識と独学勉強方法を簡単に学ぼう！当ブログ【スタビジ】の本記事では、統計学入門に必要な知識をカンタンにまとめ、それらをどのように効率的に独学で勉強していけばよいかをお話ししていきます。統計学は難しいイメージが少しありますが、学び方をしっかり考えれば大丈夫！ 【入門】機械学習のアルゴリズム・手法をPythonとRの実装と一緒に解説！当サイト【スタビジ】の本記事では、入門者向けに機械学習についてカンタンにまとめていきます。最終的にはどのように機械学習を学んでいけばよいかも見ていきます。細かい手法の実装もPython/Rを用いておこなっていくので適宜参考にしてみてください。

また、当メディアではデータサイエンティストになるための分野を体系的に学ぶスクールを運営しておりますので、データサイエンス全般に興味のある方は是非チェックしてみてください！