スタビジ
スタアカで学ぶ
カテゴリ

Webマーケ

Webマーケの記事すべてSEOサイト運営データマネジメントビジネス・マーケ概論広告

インタビュー

インタビューの記事すべて

おすすめサービス

おすすめサービスの記事すべて

おすすめ勉強法

おすすめ勉強法の記事すべて

おすすめ書籍

おすすめ書籍の記事すべて

データサイエンス

データサイエンスの記事すべてデータ解析品質工学多変量解析機械学習統計学

プログラミング

プログラミングの記事すべてPythonRSQLプログラミングスクール

スタビジについて

記事一覧運営者情報お問い合わせ

【3分で分かる】T法とシミュレーション実験

公開 更新 読了 約15分
目次
ウマたんウマたん

本記事では、タグチメソッドの回帰手法「T法」についてまとめていきます。重回帰分析では、説明変数から目的変数が発生していると考えています。一方でT法では、目的変数から説明変数が発生していると考えています。

T法とは、タグチ流の多変量解析手法の一つであり予測のための方法です。

T法について細かく見ていきましょう！

T法とは？

用いられる、データタイプは重回帰分析と同じです。

つまり、一つの目的変数と複数の説明変数があり、連続変量を考えています。

重回帰分析との違いは、データ発生の背景にあります。

重回帰分析では、説明変数から目的変数が発生していると考えています。

一方でT法では、目的変数から説明変数が発生していると考えています。

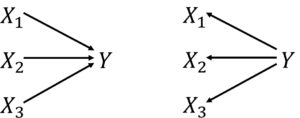
左図：重回帰のモデル（説明変数は独立）、右図：T法のモデル

T法では、「重り」と「秤」のモデルとしてよく知られています。

一つの「重り」を複数の「秤」で測ったときにそれぞれの秤の重要性によって総合して「重り」の重さを推定する方法と考えられています。

秤の重要性はSN比と呼ばれます。

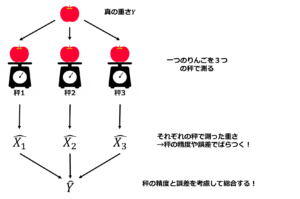
図：重りと秤の図

T法の解析手順

T法による解析の手順は以下の通りです。

  1. 学習データの中から目的変数が中位にあるmm個のデータを単位空間とします。学習データから単位空間の平均を引くことでデータの基準化を行います。
    \begin{eqnarray*}
    \bar{x}_{j}&=&\frac{1}{m}\sum_{i=1}^n{x^{unit}_{ij}}, \bar{y}=\frac{1}{m}\sum_{i=1}^n{y^{unit}_{i}}\\
    X_{ij}&=&x^{signal}_{ij}-\bar{x}_{j}, M_{i}=y^{signal}_{i}-\bar{y}\\
    \end{eqnarray*}

  2. 比例定数βj^\hat{\beta_j}とSN比ηj^\hat{\eta_j}を算出します。
    \begin{eqnarray*}
    \hat{\beta_j}&=&\frac{\sum_{i=1}^lX_{ij}M_i}{r}\\
    \hat{\eta_j}&=&
    \begin{cases}
    \frac{\frac{1}{r}(S_{\beta_j}-V_{e_j})}{V_{e_j}} & (S_{\beta_j}>V_{e_j})\\
    0 & (S_{\beta_j} \leq V_{e_j})
    \end{cases} \\
    r&=&{\sum_{i=1}^lM_{i}^2}\\
    S_{T_j}&=&{\sum_{i=1}^lX_{ij}^2}\\
    S_{\beta_j}&=&\frac{(\sum_{i=1}^lX_{ij}M_i)^2}{r}\\
    S_{e_j}&=&S_{T_j}-S_{\beta_j}\\
    V_{e_j}&=&\frac{S_{e_j}}{l-1}\\
    \end{eqnarray*}

  3. 逆推定をすることで各説明変数に対する目的変数の推定値M^ij\hat{M}_{ij}を求めます。
    M^ij=Xijβj^\displaystyle \hat{M}_{ij}=\frac{X_{ij}}{\hat{\beta_j}}

  4. 各説明変数に対する目的変数の推定値M^ij\hat{M}_{ij}をSN比ηj^\hat{\eta_j}によって重み付け総合をして基準化済みの総合推定値M^i\hat{M}_{i}を算出します。
    \begin{eqnarray*}
    \hat{M}_{i}&=&\frac{1}{\sum_{j=1}^p\hat{\eta}_j}{\sum_{j=1}^p{\hat{\eta}_j\hat{M}_{ij}}}\\
    \end{eqnarray*}

  5. 単位空間の平均を加えることで基準化前の総合推定値y^i\hat{y}_{i}を求めます。
    \begin{eqnarray*}
    \hat{y}_{i}&=&\frac{1}{\sum_{j=1}^p\hat{\eta}_j}{\sum_{j=1}^p{\hat{\eta}_j\hat{M}_{ij}}}+\bar{y}\\
    \end{eqnarray*}

T法の計算詳細

ここではT法の計算について比例項による変動とSN比の算出の仕方の説明します。

また、比例定数の二乗の推定値の求め方からもう一つのSN比が用いられることがあるのでその紹介をします。

まず、T法のモデル次は次のように式で表されます。
\begin{eqnarray*}
X_{ij}&=&\beta_jM_i+\epsilon_{ij},\epsilon_{ij} \sim N(0,\sigma_j^2)\\
\end{eqnarray*}

T法における比例項による変動SβjS_{\beta_j}は次のように求めています。
\begin{eqnarray*}
S_{\beta_j}&=&{\sum_{i=1}^l\hat{X}_{ij}^2}\\
&=&{\sum_{i=1}^l{(\hat{\beta}_jM_i)}^2}\\
&=&{\sum_{i=1}^l{\left(\frac{\sum_{t=1}^lX_{tj}M_t}{r}M_i\right)}^2}\\
&=&{\sum_{i=1}^l{\frac{\left({\sum_{t=1}^lX_{tj}M_t}\right)^2}{r^2}{M_i}^2}}\\
&=&\frac{\left({\sum_{t=1}^lX_{tj}M_t}\right)^2}{r^2}{\sum_{i=1}^l{{M_i}^2}}\\
&=&\frac{\left({\sum_{i=1}^lX_{ij}M_i}\right)^2}{r}\\
\end{eqnarray*}
続いてSN比ηj\eta_jの定義は
\begin{eqnarray*}
\eta_j&=&\frac{\beta_j^2}{\sigma_j^2}
\end{eqnarray*}
であるので、η^j\hat{\eta}_jは
\begin{eqnarray*}
\hat{\eta}_j&=&\frac{\hat{\beta}_j^2}{\hat{\sigma}_j^2}
\end{eqnarray*}
となります。σ^j2\hat{\sigma}_j^2は誤差分散の推定値を表すのでVejV_{e_j}になります。
そしてβ^j2\hat{\beta}_j^2は二つの計算方法があります。
一つ目は、β^j\hat{\beta}_jの二乗つまりβj\beta_jの推定値の二乗を用いる方法です。
この場合、η^j\hat{\eta}_jは
\begin{eqnarray*}
\hat{\eta}_j&=&\frac{\hat{\beta}_j^2}{\hat{\sigma}_j^2}\\
&=&\frac{\left({\frac{\sum_{i=1}^lX_{ij}M_i}{r}}\right)^2}{V_{e_j}}\\
&=&\frac{{\frac{1}{r}}S_{\beta_j}}{V_{e_j}}\\
\end{eqnarray*}
となります。
二つ目は、βj2\beta_j^2の推定値を用いる（推定値の二乗ではなく二乗の推定値を用いる）方法です。
βj2\beta_j^2の推定値はβj2\beta_j^2とSβjS_{\beta_j}の関係から次のように求めます。
\begin{eqnarray*}
S_{\beta_j}&=&\frac{\left({\sum_{i=1}^lX_{ij}M_i}\right)^2}{r}\\
E[S_{\beta_j}]&=&E\left[\frac{\left({\sum_{i=1}^lX_{ij}M_i}\right)^2}{r}\right]\\
&=&\frac{1}{r}E\left[\left({\sum_{i=1}^lX_{ij}M_i}\right)^2\right]\\
&=&\frac{1}{r}\left(E\left[{\sum_{i=1}^lX_{ij}M_i}\right]^2+V\left[{\sum_{i=1}^lX_{ij}M_i}\right]\right)\\
\end{eqnarray*}
ここで、
\begin{eqnarray*}
E\left[{\sum_{i=1}^lX_{ij}M_i}\right]&=&{\sum_{i=1}^l{E[X_{ij}]}M_i}\\
&=&{\sum_{i=1}^l(\beta_jM_i)M_i}=\beta_j{\sum_{i=1}^lM_i^2}=\beta_jr\\
V\left[{\sum_{i=1}^lX_{ij}M_i}\right]&=&{\sum_{i=1}^l{V[X_{ij}]}M_i^2}\\
&=&{\sum_{i=1}^l{\sigma_j^2}M_i^2}=\sigma_j^2r\\
\end{eqnarray*}
であるので、
\begin{eqnarray*}
E[S_{\beta_j}]&=&\frac{1}{r}\left(E\left[{\sum_{i=1}^lX_{ij}M_i}\right]^2+V\left[{\sum_{i=1}^lX_{ij}M_i}\right]\right)\\
&=&\frac{1}{r}\left((\beta_jr)^2+(\sigma_j^2r)\right)\\
&=&\beta_j^2r+\sigma_j^2\\
\end{eqnarray*}
となります。したがって、
\begin{eqnarray*}
\beta_j^2&=&\frac{1}{r}\left(E[S_{\beta_j}]-\sigma_j^2\right)\\
\hat{\beta}_j^2&=&\frac{1}{r}\left(S_{\beta_j}-V_{e_j}\right)\\
\end{eqnarray*}

この場合、η^j\hat{\eta}_jは
\begin{eqnarray*}
\hat{\eta}_j&=&\frac{\hat{\beta}_j^2}{\hat{\sigma}_j^2}\\
&=&\frac{\frac{1}{r}\left(S_{\beta_j}-V_{e_j}\right)}{V_{e_j}}\\
\end{eqnarray*}

この二つの違いは式を見ればVejV_{e_j}を引くかどうかになっています。

田口玄一氏がT法を考案されたときは二つ目の方法でSN比を算出しています。

一方で、近年の論文では一つ目の方法を用いているものも多いです。

一つ目の方法は場合分けの必要がなく簡便です。

二つ目の方法はVejV_{e_j}がSβjS_{\beta_j}よりも大きい場合にはその項目のSN比は0と定義するので変数選択がされます。

しかし、全てのSN比が0になる場合もありそのときには総合推定値が計算不可能になってしまいます。

結局どちらの方法もηj\eta_jの不偏推定量ではないのでどちらが良いかは分かりませんが、僕としては計算が簡便な一つ目の方法をおすすめします。

T法を使ったシミュレーション実験

続いてT法と重回帰分析をシミュレーション実験によって精度比較をしてみたいと思います！

まず、T法の計算について少しおさらいします。T法は個々の説明変数と目的変数とで逆単回帰を行い、変数毎の逆推定値を比例定数とSN比によって重み付け総合することで目的変数の総合推定値を算出します。総合推定値の式は次のようになりました。

\begin{eqnarray*}
\hat{y}_{i}&=&\frac{1}{\sum_{j=1}^p\hat{\eta}_j}\sum_{j=1}^p{\hat{\eta}_j}\frac{X_{ij}}{\hat{\beta_j}}+\bar{y}\\
\end{eqnarray*}

ここで、
\begin{eqnarray*}
\hat{\alpha}_{h}&=&\frac{\hat{\eta}_h}{\hat{\beta_h}\sum_{j=1}^p\hat{\eta}_j}\\
\end{eqnarray*}

とおくと、
\begin{eqnarray*}
\hat{y}_{i}&=&\sum_{j=1}^p{\hat{\alpha}_j}{X_{ij}}+\bar{y}\\
\end{eqnarray*}

と表記出来ます。
よって、T法の総合推定値も重回帰モデルっぽく書くことが出来るわけです。
そこで、まず重回帰モデルの人工データで比較してみます。
比較手法としては重回帰、Lasso、Rdigeを取り上げます。

ただ比較において注意が必要で、厳密にはT法は学習データを単位空間と信号空間に分けて解析を行います。

信号空間は単位空間の平均によって基準化され、モデルは信号空間のデータのみで構築されます。しかし、それでは重回帰やLasso・Ridgeとはモデル構築用のデータ数が異なってしまいます。

そこで、今回はT法ではなく拡張手法であるTa法を用います。Ta法は単位空間を設定せずに全ての学習データの平均を用いて基準化する方法です。T法の拡張手法に関して詳しくは以下の記事で！

Ta法・Tb法こんにちは！

実験の設定と手順

・比較手法：重回帰・Lasso回帰・Ridge回帰・Ta法

・評価指標：MSPE(平均二乗予測誤差)

・シミュレーション回数：100回

実験の流れは簡単にこんな感じです。

  1. 人工データを生成
  2. データを解析
  3. 指標を算出して結果を格納
  4. 1~3を100回繰り返す
  5. 結果の平均とばらつきで比較

人工データ生成

今回のデータの生成モデルを次に示します。

\begin{eqnarray*}
y_i&=&1+{\bf x}_i^T{\bf \beta}+\epsilon_i\\
{\bf \beta}&=&(\beta_1,\beta_2,0,\cdots,0)^T\in {\bf R}^p\\
{\bf x_i}&\sim& N({\bf \mu},{\bf \Sigma})\\
{\bf \mu}&=&{\bf 0}_p\\
{\bf \Sigma}&=&{\bf I}_p\\
\epsilon_i&\sim& N(0,1^2)\\
i&=&1,2,\cdots,n\\
\end{eqnarray*}

説明変数はpp次元であり、平均0・独立で発生させています。
また、β\betaはpp次元ベクトルであり、変数1と変数2のみが目的変数へ寄与があります。
今回は、ppを5と100の場合で実験します。

シミュレーション開始

シミュレーション実験をしてみましょう。
サンプルサイズn=ntrain+ntestn=n_{train}+n_{test}はテストデータのサンプルサイズntestn_{test}は1000として、学習データのサンプルサイズntrainn_{train}は変化させます。

今回用いるコード（p=5,ntrain=20p=5,n_{train}=20の場合）を載せておきます。
実行する前に入っていないパッケージはインストールしておいてください。
ちなみにT法（Ta法）についてはMTSYSというパッケージを用いています。MTSYSにはMT法やRT法も入っています。
MTSYSを用いたTa法を実行するやり方の詳細はこちらへ！

MTシステムを実装出来るRパッケージここではMTシステムを実装するのに便利なR言語のMTSYSパッケージを紹介します。 
library(MASS)
library(mvtnorm)
library(glmnet)
library(MTSYS)
library(ggplot2)
library(tidyr)

times <- 100

n_train <- 20
n_test <- 1000
p <- 5

β0 <- 1 ##定数項
β <- c(1,-1,numeric(p-2))
β <- c(β0,β)

μ <- numeric(p)
Σ <- diag(p)

σ <- 1 ##誤差標準偏差

MSPE <- data.frame(glm=numeric(times)+NaN, lasso=numeric(times)+NaN,
                   ridge=numeric(times)+NaN, Ta=numeric(times)+NaN)

for(t in 1:times){
  X <- rmvnorm((n_train+n_test),μ,Σ)
  X <- cbind(rep(1,(n_train+n_test)),X)
  ε <- rnorm((n_train+n_test),0,σ)
  y <- X%*%β+ε
  
  data <- cbind(X,y)
  data <- as.data.frame(data)
  colnames(data) <- c("Int",paste0('x', 1:p),"y")
  
  ##学習データとテストデータを作成
  data_train <- data[1:n_train,]
  data_test <- data[-(1:n_train),]
  
  ##glm(普通の線形回帰)
  result_glm <- glm(formula=y~., data=data_train[,colnames(data_train)!="Int"], family=gaussian(link="identity"))
  
  ##glmnet(lasso)
  result_lasso <- cv.glmnet(x=as.matrix(data_train[,!(colnames(data_train) %in% c("Int","y"))]), 
                            y=data_train$y, family="gaussian",alpha=1)
  
  ##glmnet(ridge)
  result_ridge <- cv.glmnet(x=as.matrix(data_train[,!(colnames(data_train) %in% c("Int","y"))]), 
                            y=data_train$y, family="gaussian",alpha=0)
  
  ##MTSYS(Ta)
  result_Ta <- Ta(sample_data = data_train[, colnames(data_train) != "Int"],
                 subtracts_V_e = TRUE,
                 includes_transformed_data = TRUE)
  

  
  ##予測誤差を算出
  yhat_glm <- as.matrix(data_test[,colnames(data_test)!="y"])%*%as.matrix(result_glm$coefficients)
  MSPE$glm[t] <- mean((data_test$y-yhat_glm)^2)
  
  yhat_lasso <- as.matrix(data_test[,colnames(data_test)!="y"])%*%coefficients(result_lasso,s="lambda.min")
  MSPE$lasso[t] <- mean((data_test$y-yhat_lasso)^2)
  
  yhat_ridge <- as.matrix(data_test[,colnames(data_test)!="y"])%*%coefficients(result_ridge,s="lambda.min")
  MSPE$ridge[t] <- mean((data_test$y-yhat_ridge)^2)
  
  yhat_Ta <- forecasting(model = result_Ta,
                                newdata = data_test[, -which (colnames(data_test) %in% c("Int", "y"))],
                                includes_transformed_newdata = TRUE)$y_hat
  MSPE$Ta[t] <- mean((data_test$y-yhat_Ta)^2)
  
  cat("t=",t," ")
}

##ggplotで箱ひげ図を描く
g <- ggplot(gather(MSPE), aes(y=value,x=key))
g <- g + geom_boxplot()
g <- g + xlab("Method")
g <- g + ylab("MSPE")

plot(g)

ばらつきも含めて見たいので結果を箱ひげ図で表します。
重回帰はglmと表記してあります。

・p=5,ntrain=20p=5, n_{train}=20の結果

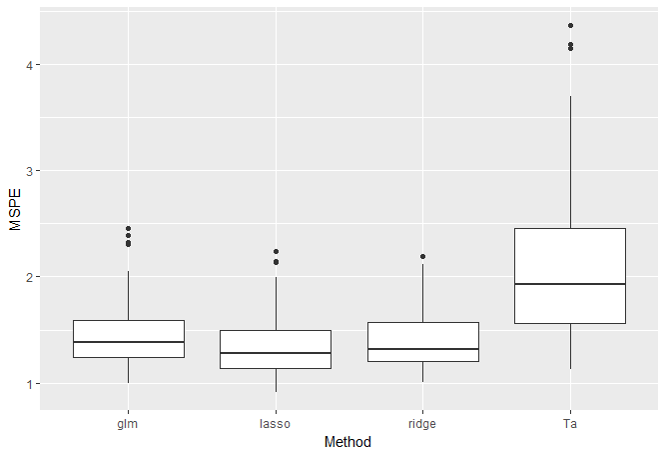
やはり説明変数の数も多くないのでどの手法も同程度ですね。

・p=5,ntrain=1000p=5, n_{train}=1000の結果
学習データ数をかなり多くした結果です。

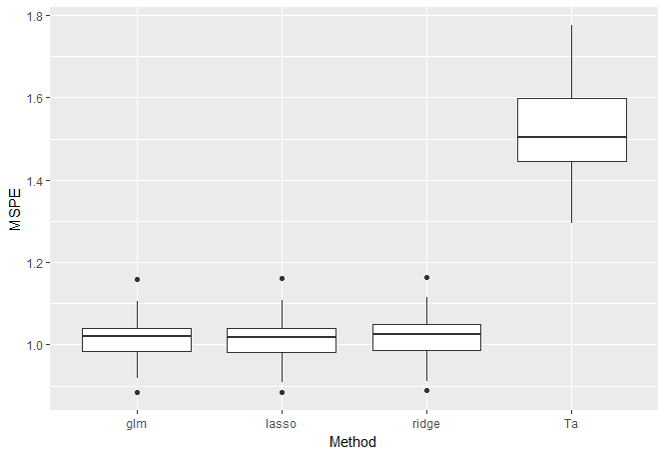
傾向はntrain=20n_{train}=20のときと変わりません。ここで、推定された係数を見てみましょう。

・重回帰

> as.matrix(result_glm$coefficients)
[,1]
(Intercept) 0.96814597
x1 1.01957322
x2 -0.99977962
x3 0.02176648
x4 0.04343735
x5 -0.00206636

・Lasso

> coefficients(result_lasso,s="lambda.min")
6 x 1 sparse Matrix of class "dgCMatrix"
1
(Intercept) 0.96733620
x1 0.99592767
x2 -0.97756963
x3 .
x4 0.02051056
x5 .

・Rdige

> coefficients(result_ridge,s="lambda.min")
6 x 1 sparse Matrix of class "dgCMatrix"
1
(Intercept) 0.9675938914
x1 0.9577254944
x2 -0.9391526386
x3 0.0205584744
x4 0.0380564049
x5 -0.0004578514

・Ta

> α_hat <- t(t(((result_Ta$eta_hat)/(result_Ta$beta_hat))/sum(result_Ta$eta_hat))) > α_hat
[,1]
x1 1.512973
x2 -1.497028
x3 0.000000
x4 0.000000
x5 0.000000

重回帰・Lasso・Ridgeの３手法は似たような値になっており、Lassoだけがいくつか自動的に係数が0になっています。一方で、Ta法はいくつか自動的に係数が0になっているが、変数1，2の係数が真値と比べて大きいですね。

よって、標本サイズが大きくなっても重回帰モデルのデータにおいてTa法は重回帰分析やLasso等と同じくらいの精度にはならなそうです。

・p=100,ntrain=10p=100, n_{train}=10の結果
次に小標本高次元で実験してみます。この設定では重回帰は計算不可能なので結果から除外しています。

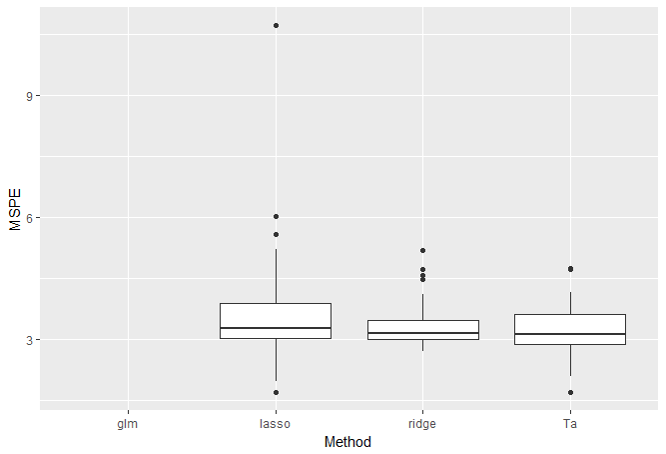
うーん。LassoよりTa法の方がよさそうではありますが、Ridgeと比べると微妙ですね。
重回帰モデルの人工データでの実験なのでこんなものでしょう。

T法を使って実データ解析

こんどは実データで実験してみます。
plsパッケージにあるgasolineデータを用います。
gasolineデータはオクタン価（１変数）とガソリンの拡散反射の近赤外線分光データ（401変数）で構成されています。
サンプルサイズは全部で60です。
オクタン価を近赤外線分光データで説明するモデルを構築して精度比較してみましょう。

学習データとしてランダムに30サンプルを抽出、残ったデータをテストデータとします。

  1. 学習データとしてランダムに30サンプルを抽出、残ったデータをテストデータとする。
  2. データを解析
  3. 指標を算出して結果を格納
  4. 1~3を100回繰り返す
  5. 結果の平均とばらつきで比較

実データ解析で用いたプログラムは以下の通りです。

library(MASS)
library(mvtnorm)
library(glmnet)
library(MTSYS)
library(ggplot2)
library(tidyr)
library(pls)

times <- 100

n_train <- 30 # < 60
n_test <- nrow(as.matrix(gasoline))-n_train
p <- ncol(as.matrix(gasoline))-1


MSPE <- data.frame(lasso=numeric(times)+NaN, ridge=numeric(times)+NaN, Ta=numeric(times)+NaN)

for(t in 1:times){
  data <- data.frame(Int = rep(1,nrow(as.matrix(gasoline))), as.matrix(gasoline)[,c((1+1):(p+1))],
                     octane = gasoline$octane)

  sample_train <- sample(1:nrow(gasoline),n_train)

  ##学習データとテストデータを作成
  data_train <- data[sample_train,]
  data_test <- data[-sample_train,]
  
  ##glmnet(lasso)
  result_lasso <- cv.glmnet(x=as.matrix(data_train[,!(colnames(data_train) %in% c("Int", "octane"))]), 
                            y=data_train$octane, family="gaussian",alpha=1)
  
  ##glmnet(ridge)
  result_ridge <- cv.glmnet(x=as.matrix(data_train[,!(colnames(data_train) %in% c("Int", "octane"))]), 
                            y=data_train$octane, family="gaussian",alpha=0)
  
  ##MTSYS(Ta)
  result_Ta <- Ta(sample_data = data_train[, colnames(data_train) != "Int"],
                  subtracts_V_e = TRUE,
                  includes_transformed_data = TRUE)
  
  ##予測誤差を算出
  yhat_lasso <- as.matrix(data_test[,colnames(data_test)!="octane"])%*%coefficients(result_lasso,s="lambda.min")
  MSPE$lasso[t] <- mean((data_test$octane-yhat_lasso)^2)
  
  yhat_ridge <- as.matrix(data_test[,colnames(data_test)!="octane"])%*%coefficients(result_ridge,s="lambda.min")
  MSPE$ridge[t] <- mean((data_test$octane-yhat_ridge)^2)
  
  yhat_Ta <- forecasting(model = result_Ta,
                         newdata = data_test[, -which (colnames(data_test) %in% c("Int", "octane"))],
                         includes_transformed_newdata = TRUE)$y_hat
  MSPE$Ta[t] <- mean((data_test$octane-yhat_Ta)^2)
  
  cat("t=",t," ")
}

##ggplotで箱ひげ図を描く
g <- ggplot(gather(MSPE), aes(y=value,x=key))
g <- g + geom_boxplot()
g <- g + xlab("Method")
g <- g + ylab("MSPE")

plot(g)

結果は次のようになりました。

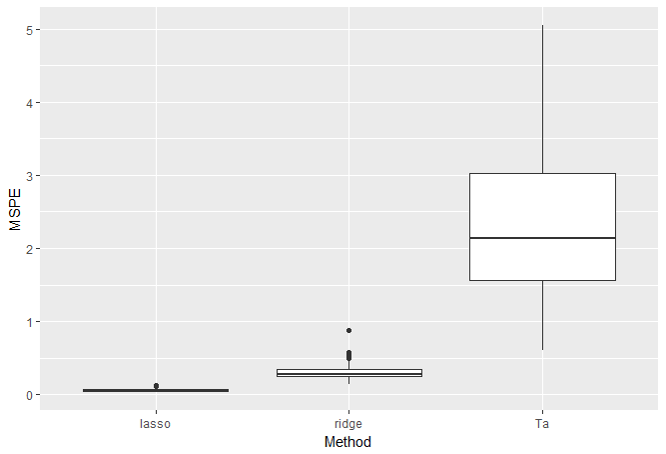
Ta法は全然良くないですね（笑）
というのもこのデータは説明変数間の相関が非常に高いデータとなっています。T法（Ta法）は多重共線性が起きていても解析出来る手法ではありますが多重共線性を克服しているわけではありません。

人工データでの実験のときは説明変数間は独立であったためそこそこの精度を保てていました。

では、T法（Ta法）は使えない手法なのかというとそうとも言えません。T法は変数毎に逆単回帰を行っているだけなので逆行列の計算が必要なく非常に計算が簡便です。エクセルでも簡単に計算することが出来て、統計手法に慣れていない方でも直観的に解釈しやすい手法だと思います。

ただ、まだ適用場面が限定的であることは否めません。T法はロジスティック回帰やポアソン回帰を用いるような目的変数が二値データやカウントデータへ適用する研究は不十分ですし、説明変数に質的データがあるときも適用が難しいです。

まだまだ、課題があるT法という手法ですが、解析する環境やデータの性質によっては使用すると良いかもしれません。

T法　まとめ

本記事では、t法の詳細やシミュレーションについて見てきました。

T法だけでなく、統計学や機械学習・データサイエンス、Pythonに興味のある方は以下の記事でまとめていますので是非チェックしてみてください！

【初心者必見】統計学入門に必要な知識と独学勉強方法を簡単に学ぼう！当ブログ【スタビジ】の本記事では、統計学入門に必要な知識をカンタンにまとめ、それらをどのように効率的に独学で勉強していけばよいかをお話ししていきます。統計学は難しいイメージが少しありますが、学び方をしっかり考えれば大丈夫！ 【5分で分かる】機械学習の独学勉強ロードマップを徹底的にまとめていく！当サイト【スタビジ】の本記事では、機械学習の独学勉強ロードマップについて徹底的にまとめていきます。機械学習をいきなり理論からしっかり勉強しようとすると挫折しかねません。そこで、この記事ではなるべく挫折しないロードマップをお伝えしてきますよ！ 【5分で分かる】データサイエンティストに必要なスキルと独学勉強ロードマップ！当サイト【スタビジ】の本記事では、データサイエンティストに求められるスキルとそれを身に付けるための勉強法について徹底的にまとめていきます！入門者でも、しっかりデータサイエンティストについて理解しある程度独学で駆け出しの状態までいけることを目指します。 【Python独学勉強法】Python入門を３ヶ月で習得できる学習ロードマップ当サイト【スタビジ】の本記事では、過去僕自身がPythonを独学を駆使しながら習得した経験をもとにPythonを効率よく勉強する方法を具体的なコード付き実装例と合わせてまとめていきます。Pythonはできることが幅広いので自分のやりたいことを明確にして勉強法を選ぶことが大事です。
スポンサーリンク

ウマたんスタビジ編集長

大学院は理系の統計科学研究室で、ベイズ統計学・時系列分析・異常検知を研究。日系・外資の消費財メーカーのデータサイエンティストを経て、現在は会社を経営しながらデータサイエンティストとして働いています。

プロフィールXYouTube
スタビジアカデミー

読んだ内容を、手を動かして身につける

データサイエンス・AIを、動画と課題で体系的に学べるオンラインスクール。

スタアカを見てみる

あわせて読みたい

品質工学の記事をもっと見る →