こんにちは！スタビジ編集部です！
機械学習について学んだことがある方は、一度は耳にしたことがあるかもしれない「最急降下法」。
しかし、「聞いたことはあるけれど、実際にどういうアルゴリズムなのかはよく分からない…」という方も多いのではないでしょうか。
本記事では、そんな方に向けて、最急降下法の基本的な仕組みからPythonによる実装方法までをわかりやすく解説します。
目次
最急降下法とは？基本概念をわかりやすく解説
最急降下法とは、目的関数の最小値を求めるための最適化アルゴリズムです。
目的関数の勾配（傾き）計算と、関数の値が最も小さくなる方向、つまり「最急降下」方向への移動を繰り返すことで、最小値を見つけていきます。
このアルゴリズムは、特に機械学習や深層学習で、モデルのパラメータを最適化する際によく使われています。
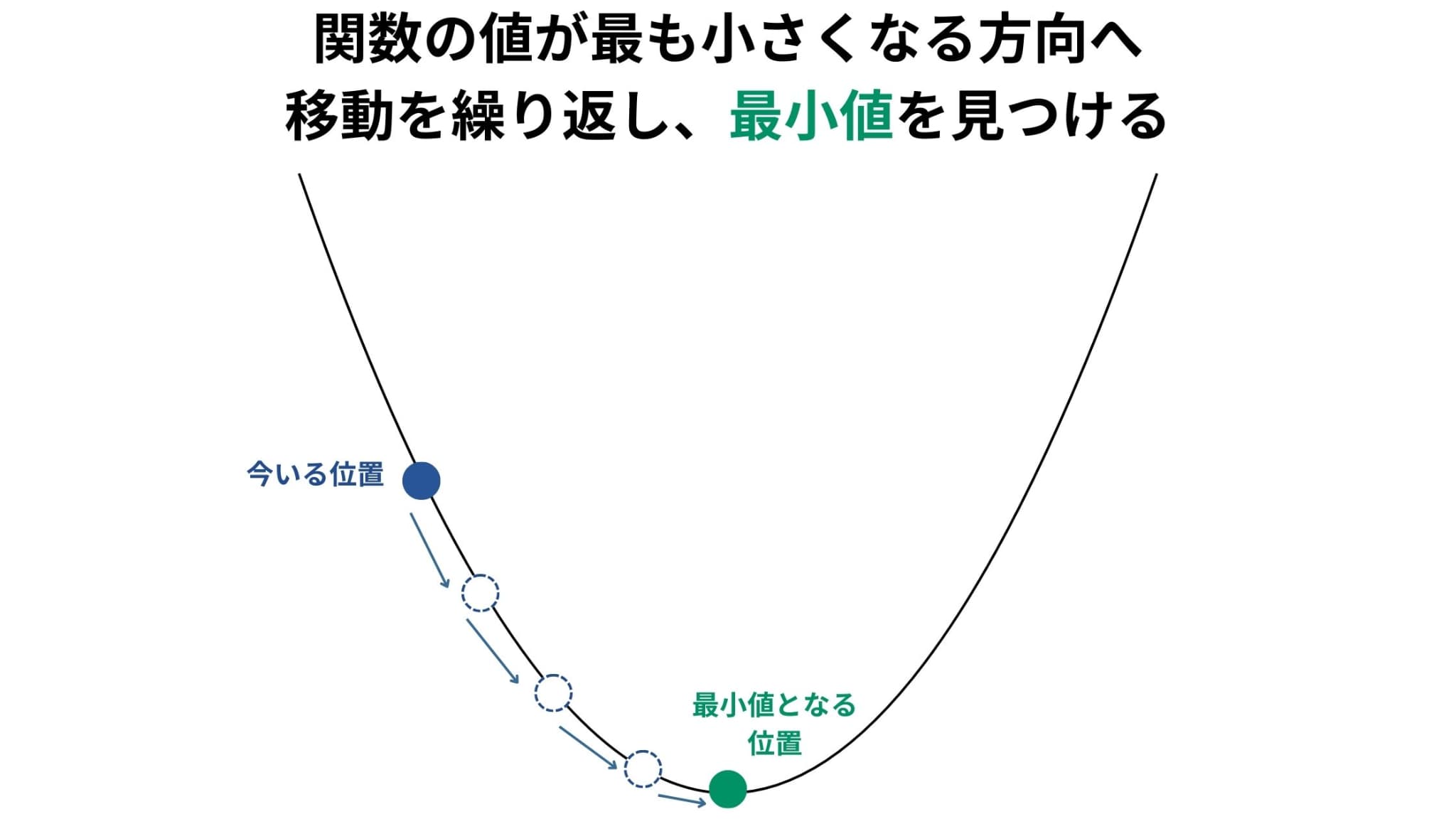
最急降下法のアルゴリズム
最急降下法のアルゴリズムは次の4ステップで説明することができます。
1. 初期位置の設定
2. 勾配（傾き）の計算
3. 位置の更新
4. 終了条件を満たすまで2~3の繰り返し
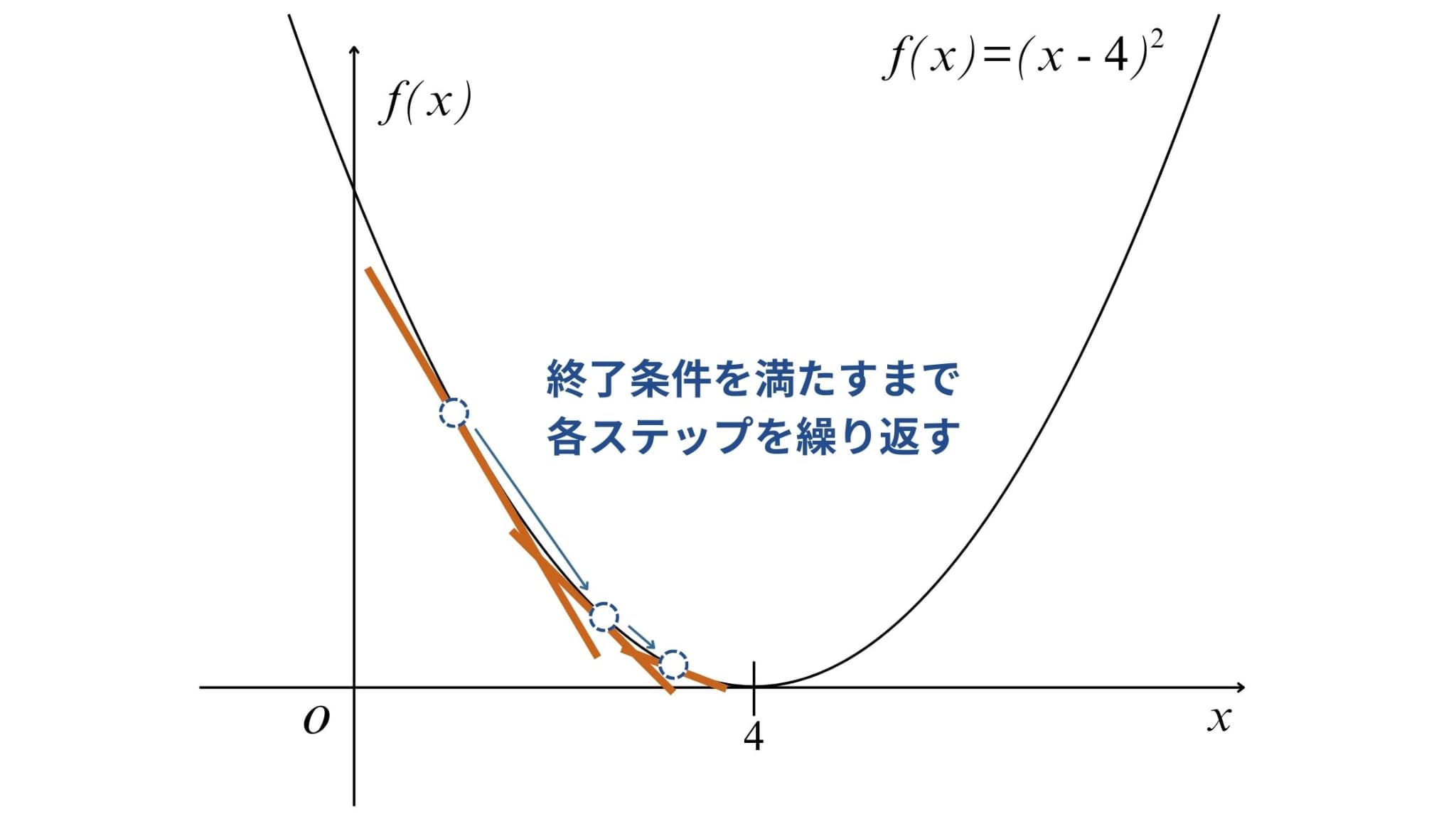
下記の目的関数を例として、各ステップについて詳しく見ていきましょう！
目的関数：\(f(x)=(x-4)^{2} \)
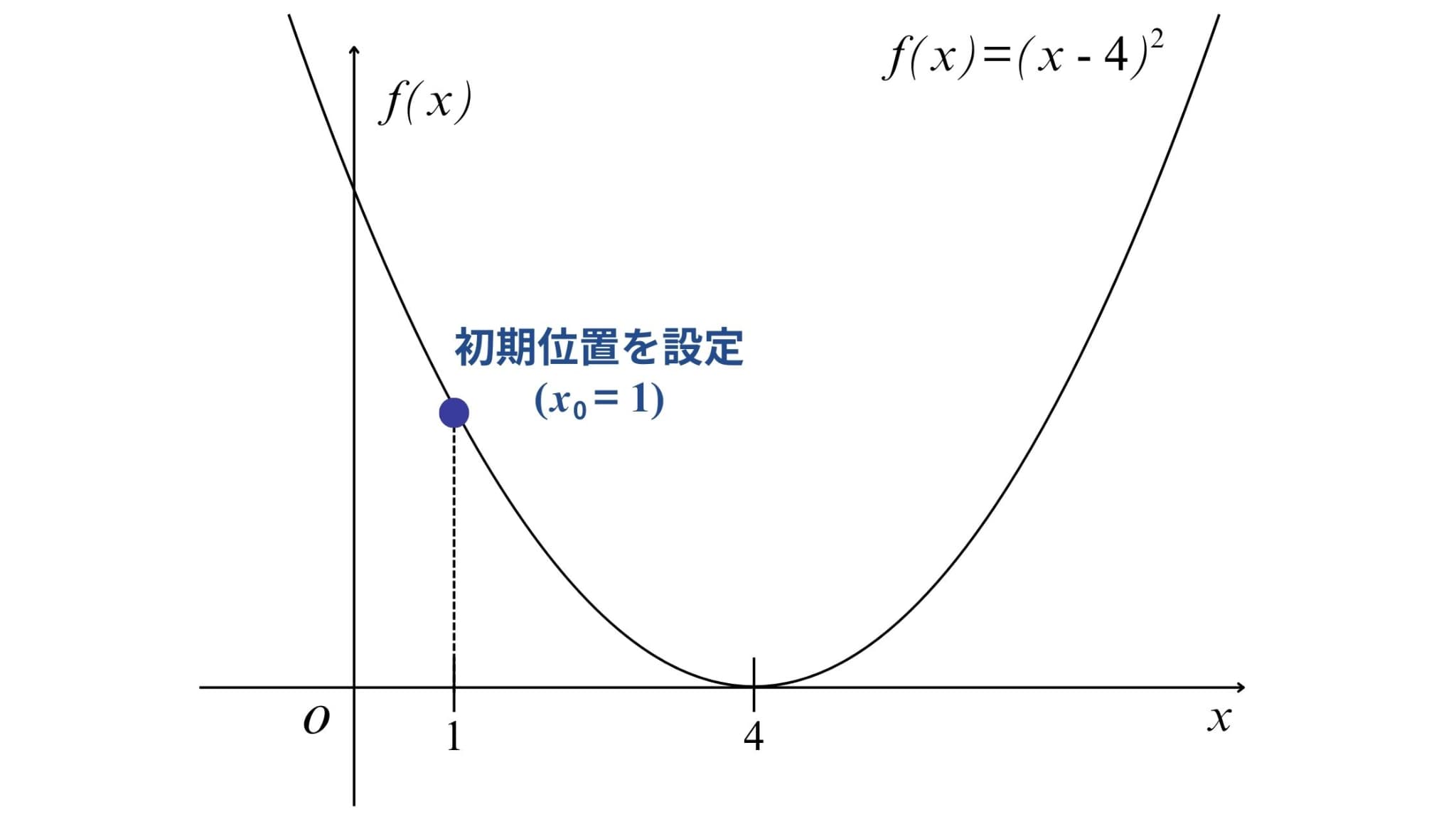
1. 初期位置の設定
まずは初期位置の設定を行います。
多くの場合ランダムに設定しますが、ひとまず今回は\(x_{0}=1\)を初期位置としてみましょう。
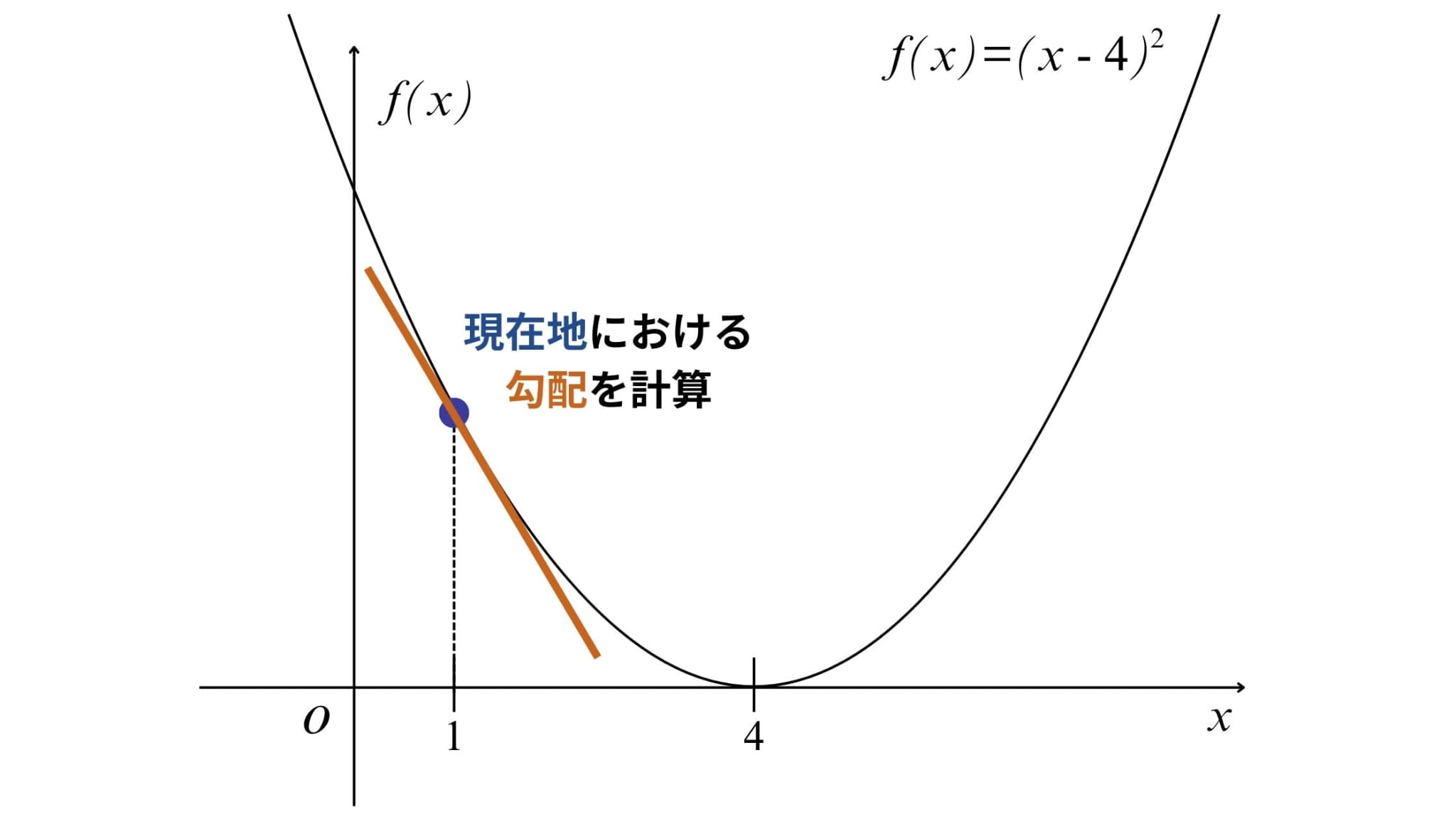
2. 勾配（傾き）の計算
続いて現在地における勾配（傾き）を計算します。
勾配は目的関数を微分すればOK！今回の場合、導関数は以下の式で表すことができます。
導関数：\(f^{‘}(x)=2x-8\)
そのため、\(x_{0}=1\)における勾配は\( f^{‘}(x_{0})=2\times1-8=-6 \)となります。
3. 位置の更新
そして、位置を更新（移動）します。
ここで必要となるのがステップ幅\(\eta\)（イータ）です。
\(\eta\)は移動する幅を決めるパラメータです。小さすぎると「ちょっとずつ進む」ため収束に時間がかかってしまい、大きすぎると「飛びすぎる」ため発散してしまう可能性があります。
そのため、移動の様子を観察しながら適切な値を見つけていく必要があります。
今回は\(\eta=0.25\)として、位置を更新してみます。
現在地を\(x_{k}\)として位置の更新を式で表すと
位置の更新：\(x_{k+1}=x_{k}-\eta\times f^{‘}(x_{k})\)
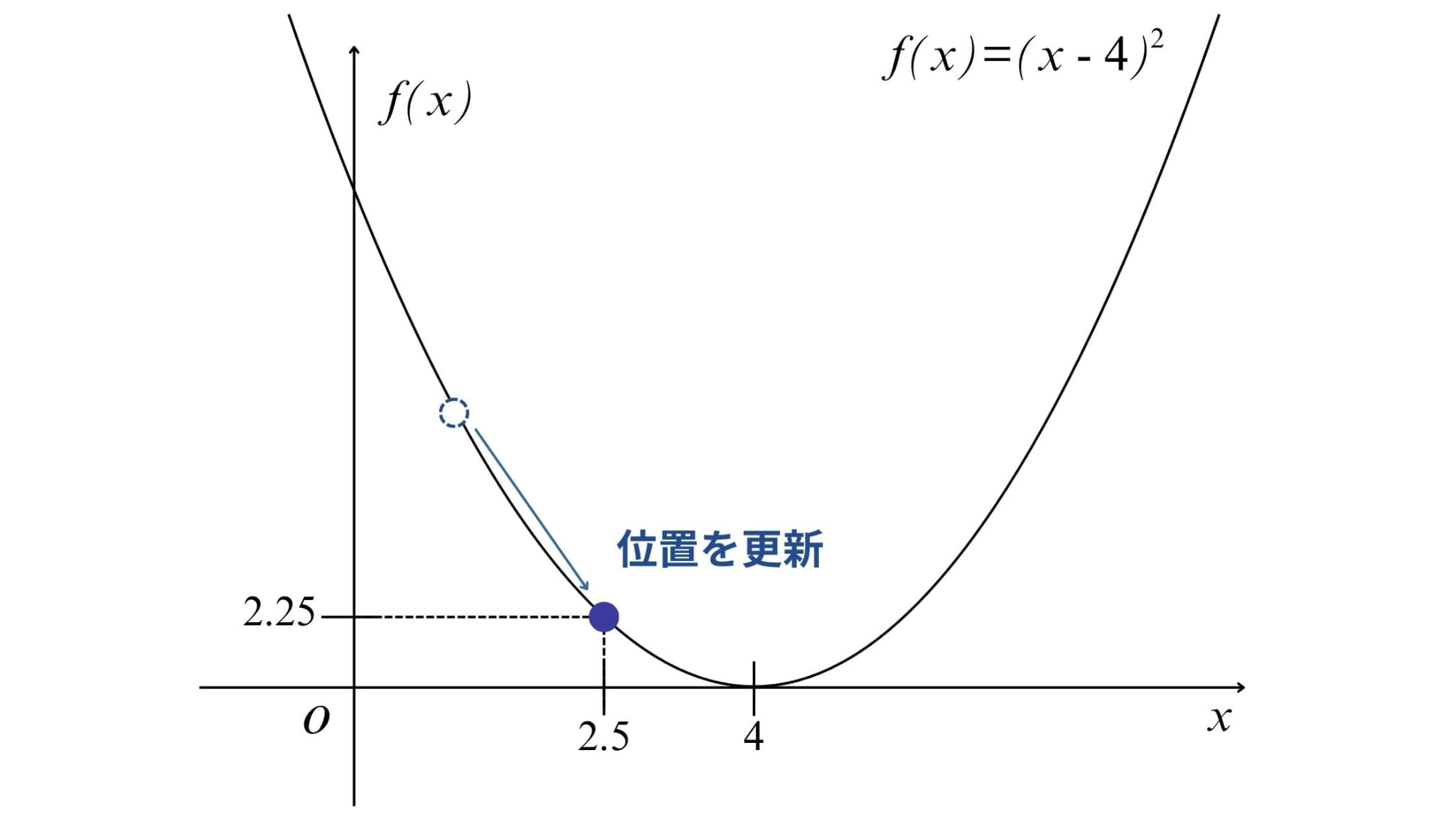
となるので、更新後の位置\(x_{1}\)は\(x_{1}=1-0.25\times -6=2.5\)となります。
このとき、目的関数の値は\(f(2.5)=(2.5-4)^{2}=2.25 \)となります。
4. 終了条件を満たすまで2~3の繰り返し
あとは2~3を繰り返し、終了条件を満たせばアルゴリズムは終了し、最小値とそのときの\(x\)の値が求まるというわけです（今回の例だと\(x=4\)のとき最小値0）。
終了条件には、「勾配の大きさが十分に小さい」、「（更新回数が）最大反復数に達したとき」などがあります。
最急降下法のメリット・デメリット
ここまで最急降下法の概要について解説してきましたが、メリットとデメリットの両方が存在します。
メリット：計算がシンプルで汎用性が高い
先ほど述べたように、最急降下法は「最急降下方向への移動を繰り返すことで、最小値を見つけていく」という、シンプルなアルゴリズムです。
故に、実装が簡単で、理解しやすい点が大きな強みです。
線形回帰・ロジスティック回帰・ニューラルネットワークなど、多くの機械学習モデルに適用することができます。
派生系アルゴリズムには以下のようなものがあります。
・SGD（確率的勾配降下法）
・モーメンタム法
・RMSProp
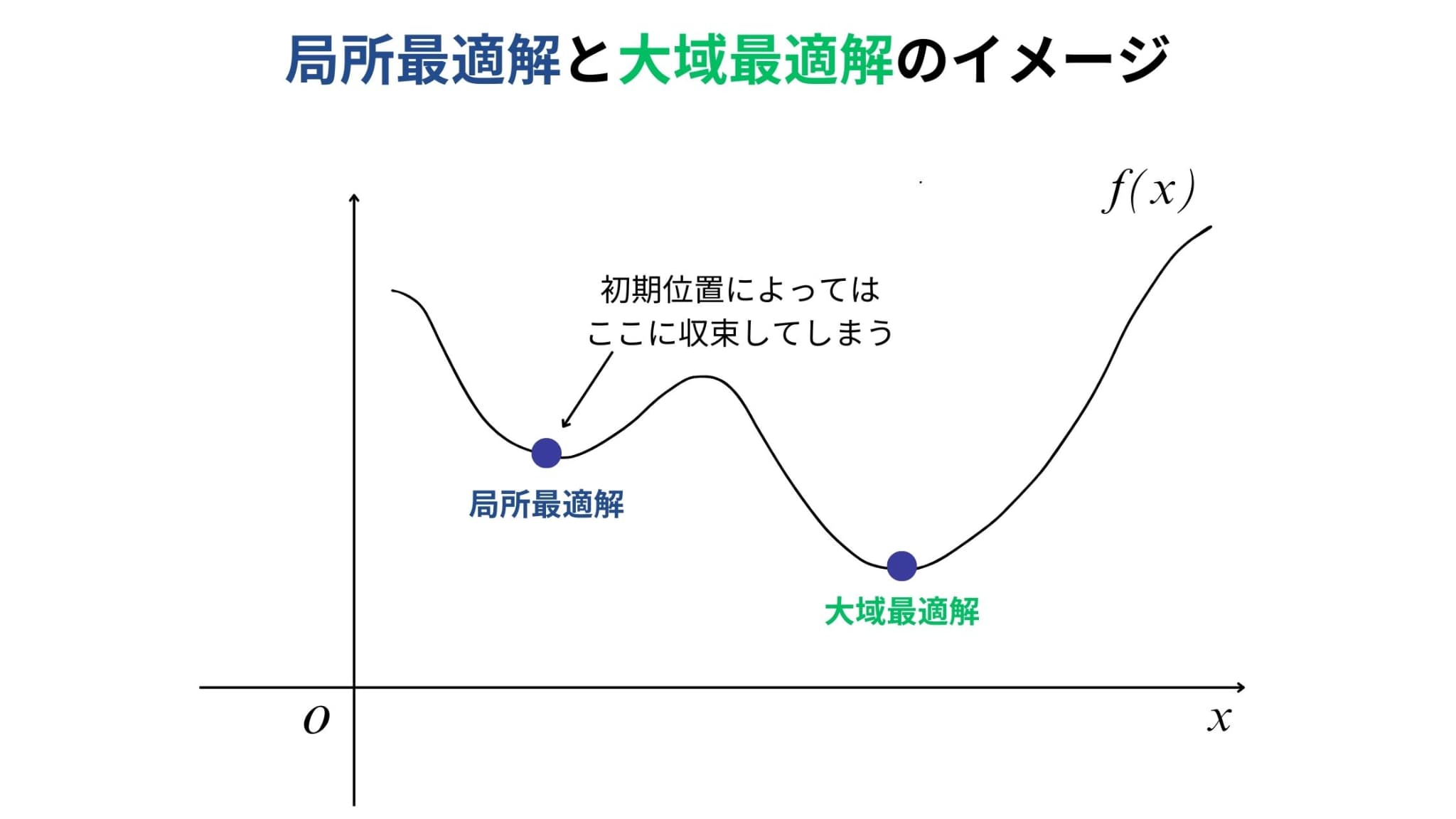
デメリット：局所最適解に陥る可能性がある
最急降下法は、初期位置を決めてそこから逐次的に最適解を探していくアルゴリズムです。
そのため局所最適解に陥ってしまい、大域最適解に到達できなくなってしまう可能性があります。
最急降下法をPythonで実装
それでは実際に最急降下法をPythonで実装していきましょう！
アルゴリズムの説明で用いた目的関数を例に実装してみます（初期位置、ステップ幅も同様）。
目的関数：\(f(x)=(x-4)^{2}\)
終了条件として、「勾配が十分小さい」または「更新回数が1,000回に達したとき」を設定しています。
import numpy as np
import matplotlib.pyplot as plt
# 目的関数 f(x) = (x - 4)^2
def f(x):
return (x - 4)**2
# 勾配（微分） f'(x) = 2(x - 4)
def df(x):
return 2 * (x - 4)
# 最急降下法の実装
def gradient_descent(df, init_x, eta=0.1, max_iter=1000, tol=1e-6):
x = init_x # 初期値を設定
history = [x] # 更新の履歴を保存
converged = False # 収束フラグ
for i in range(max_iter): # 最大反復回数までループ
grad = df(x) # 現在の点での勾配を計算
# 収束判定：勾配が十分小さければ終了
if abs(grad) < tol:
print(f"収束しました (step={i+1})")
converged = True
break
new_x = x - eta * grad # 勾配方向にステップ幅 eta で更新
history.append(new_x) # 新しい点を履歴に追加
x = new_x # 更新した値を次のステップの初期値に
# 収束しなかった場合の表示
if not converged:
print("収束しませんでした（最大反復回数に到達）")
return x, history, converged
# ===== 実行部分 =====
# 初期値を設定
x0 = 1.0
# ステップ幅（学習率）
eta = 0.25
# 最急降下法を実行
xmin, history, converged = gradient_descent(df, init_x=x0, eta=eta)
# 収束したときのみ表示
if converged:
print("推定された最小値のx:", xmin)
print("そのときのf(x):", f(xmin))
# ===== 可視化 =====
# 描画範囲の設定
x_vals = np.linspace(-1, 8, 400) # x軸の範囲
y_vals = f(x_vals) # f(x) の値を計算
plt.figure(figsize=(8, 6))
plt.plot(x_vals, y_vals, label="f(x)") # 目的関数の曲線を描画
# 更新の履歴（赤い点と軌跡）
history = np.array(history)
plt.plot(history, f(history), color="red", linestyle="--", marker="o", label="更新の軌跡")
# 収束した場合のみ最小点を強調表示
if converged:
plt.scatter(xmin, f(xmin), color="blue", s=100, label="最小値 (推定)")
# グラフの装飾
plt.title("最急降下法の収束過程（f(x) = (x-4)^2）", fontsize=14)
plt.xlabel("x")
plt.ylabel("f(x)")
plt.legend()
plt.grid(True)
plt.show()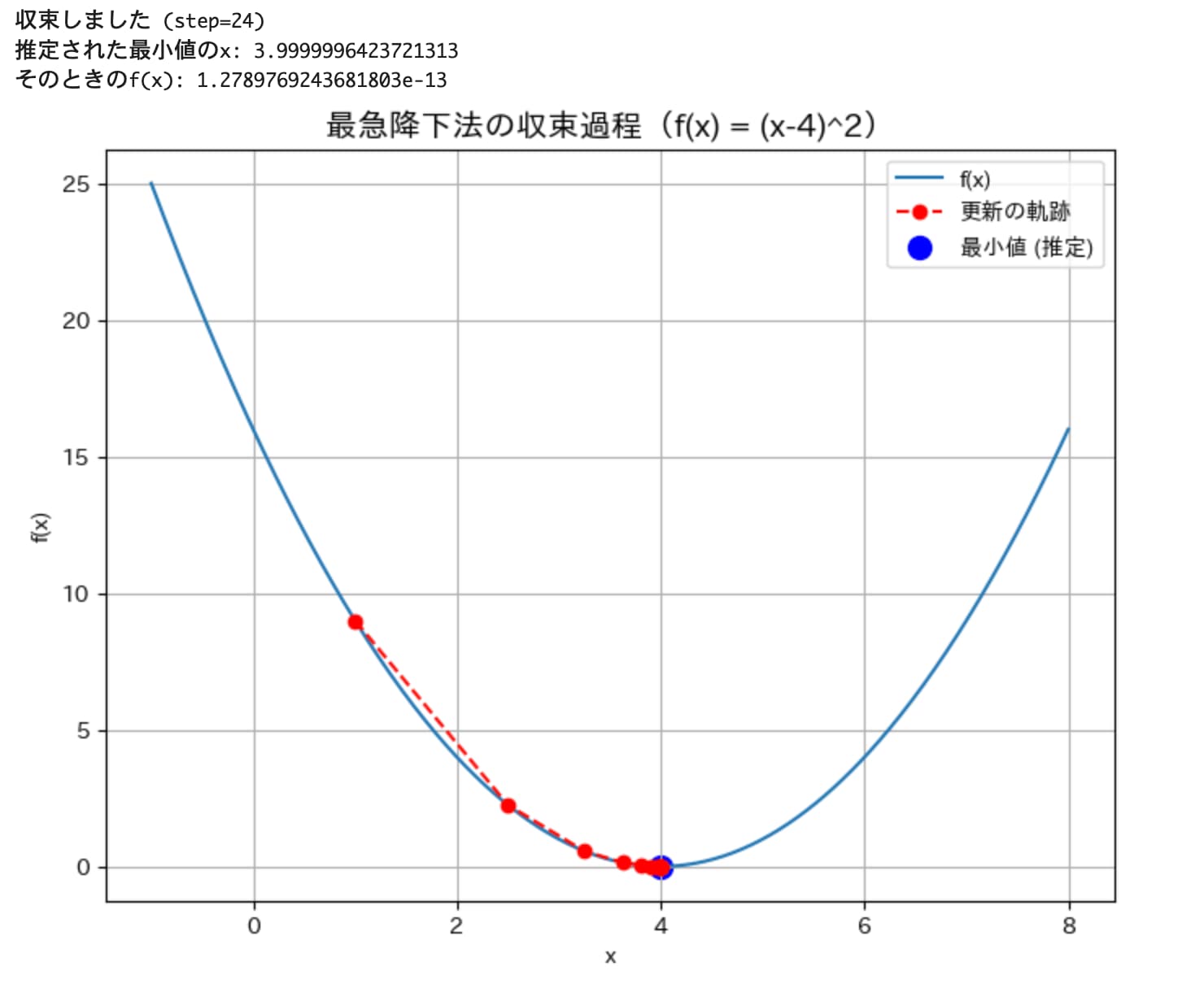
更新回数は24回で、最小値とその時の\(x\)もしっかりと求められています。
続いて、ステップ幅を小さくした場合（eta = 0.01）はどうなるでしょうか。
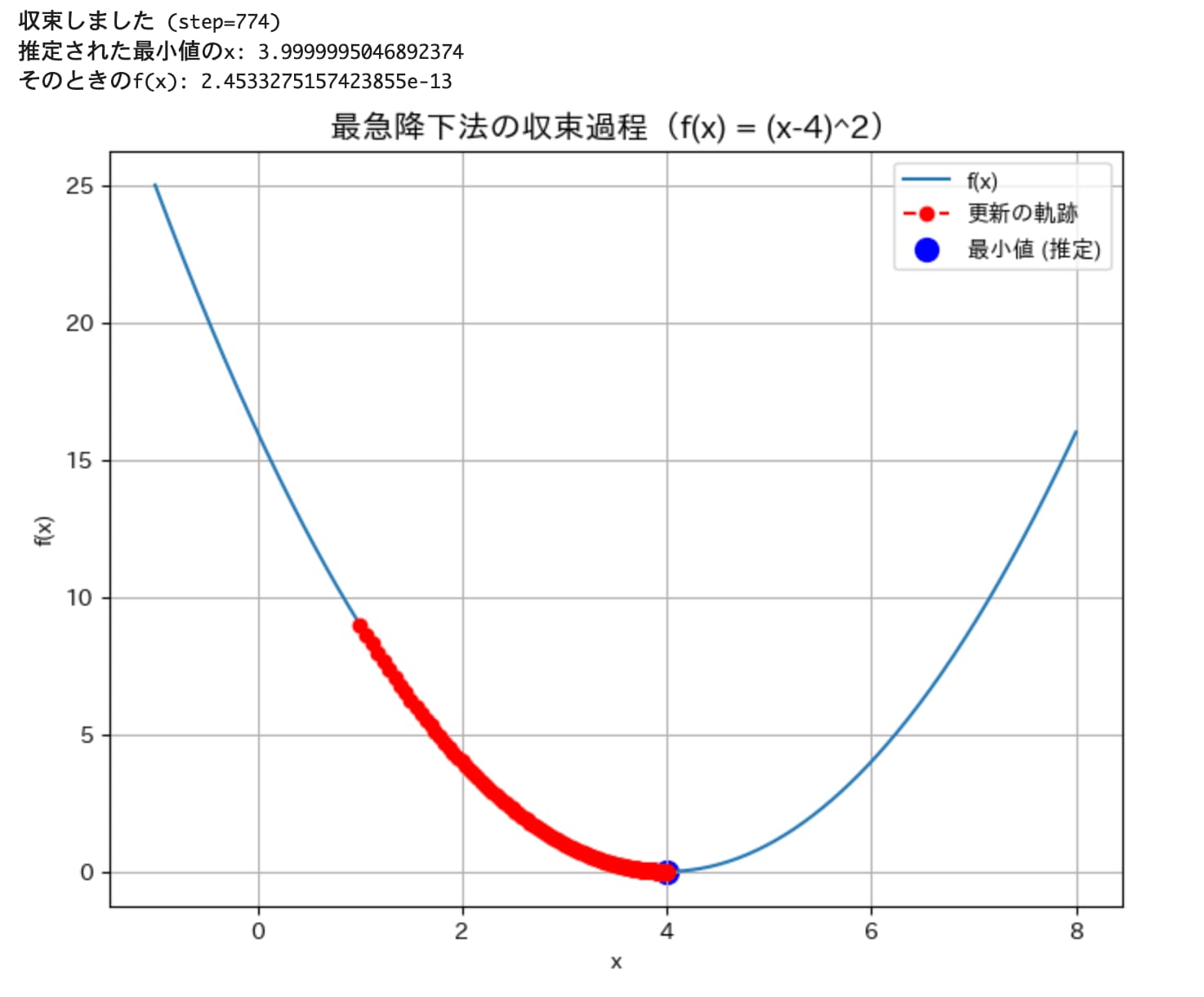
きちんと最小値を求められていますが、更新回数は774回と先ほどより大幅に増えていることがわかります。
今度はステップ幅を大きくした場合（eta = 1.0）についても見てみましょう。
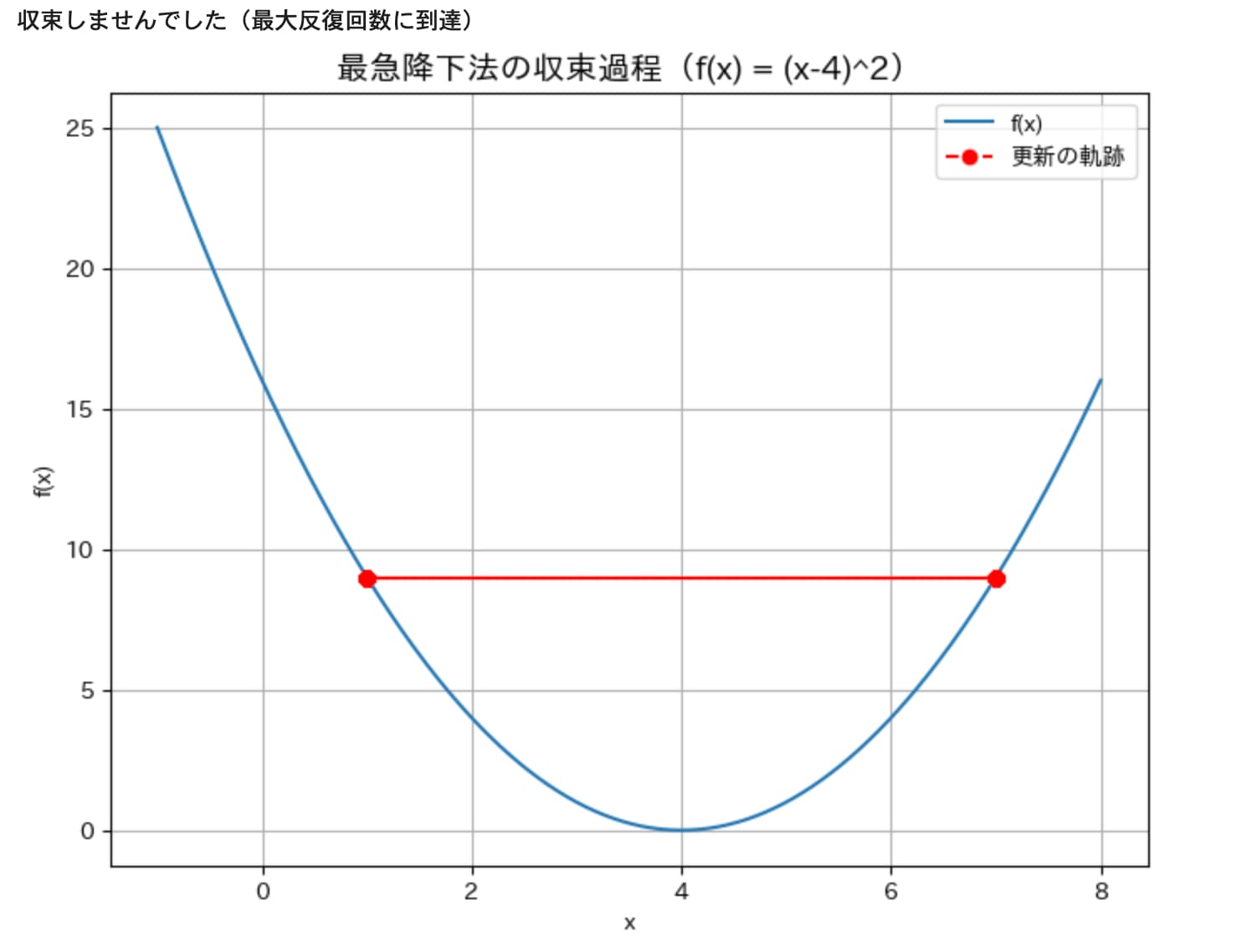
更新回数が1000回を超えても収束しませんでした（この場合、赤点の部分を繰り返し行き来しているだけとなっています）。
このように、ステップ幅の値によって、収束するか否か、または収束する速さが決まってきます。
可能であれば上図のように可視化を行い、移動の様子を観察しながら適切な値を見つけていきましょう！
最急降下法 まとめ
ここまで、最急降下法の概要とPythonでの実装方法について解説してきました。
最急降下法は「最も急な方向へ移動する」という、シンプルな手法です。
シンプルだからこそ理解しやすく、他の発展的なアルゴリズムを学ぶための出発点としても非常に重要な手法です。
これをきっかけに派生系の手法も学び、実際の問題に応じて適切な手法を選択できるようになっていきましょう！
さらに詳しくAIやデータサイエンスの勉強がしたい！という方は当サイト「スタビジ」が提供するスタビジアカデミーというサービスで体系的に学ぶことが可能ですので是非参考にしてみてください！
AIデータサイエンス特化スクール「スタアカ」
| 【価格】 | ライトプラン：1280円/月 プレミアムプラン：149,800円 |
|---|---|
| 【オススメ度】 | |
| 【サポート体制】 | |
| 【受講形式】 | オンライン形式 |
| 【学習範囲】 | データサイエンスを網羅的に学ぶ 実践的なビジネスフレームワークを学ぶ SQLとPythonを組み合わせて実データを使った様々なワークを行う マーケティングの実行プラン策定 マーケティングとデータ分析の掛け合わせで集客マネタイズ |
データサイエンティストとしての自分の経験をふまえてエッセンスを詰め込んだのがこちらのスタビジアカデミー、略して「スタアカ」！！
当メディアが運営するスクールです。
24時間以内の質問対応と現役データサイエンティストによる複数回のメンタリングを実施します！
カリキュラム自体は、他のスクールと比較して圧倒的に良い自信があるのでぜひ受講してみてください！
他のスクールのカリキュラムはPythonでの機械学習実装だけに焦点が当たっているものが多く、実務に即した内容になっていないものが多いです。
そんな課題感に対して、実務で使うことの多いSQLや機械学習のビジネス導入プロセスの理解なども合わせて学べるボリューム満点のコースになっています！
Pythonが初めての人でも学べるようなカリキュラムにしておりますので是非チェックしてみてください！
ウォルマートのデータを使って商品の予測分析をしたり、実務で使うことの多いGoogleプロダクトのBigQueryを使って投球分析をしたり、データサイエンティストに必要なビジネス・マーケティングの基礎を学んでマーケティングプランを作ってもらったり・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践してもらったりする盛りだくさんの内容になってます！
・BigQuery上でSQL、Google Colab上でPythonを使い野球の投球分析
・世界最大手小売企業のウォルマートの実データを用いた需要予測
・ビジネス・マーケティングの基礎を学んで実際の企業を題材にしたマーケティングプランの策定
・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践して稼ぐ
スタビジのコンテンツをさらに深堀りしたコンテンツが動画と一緒に学べるスクールです。
プレミアムプランでは私がマンツーマンで伴走させていただきます！ご受講お待ちしております！
