一般化線形モデルのポアソン回帰をわかりやすく解説しPythonで回帰モデル実装!

こんにちは!スタビジ編集部です!
こんな感じで、なんとなく重回帰分析を使っていませんか?
実は重回帰分析というのは線形モデルの一種であり、目的変数の分布に正規分布を仮定しているという制限があるのです。
そのため、目的変数が連続量のように見えるが実際は正の値しか取らないカウントデータであるとき、重回帰分析を行ってしまうとうまく予測ができない場合があります。
そんなときに有用なのがポアソン回帰分析!
目的変数がポアソン分布に従うときに使える、一般化線形モデルの一種です。
この記事では、そんなポアソン回帰分析について、機械学習との違いや活用例を交えて詳しく解説していきます!

以下のYoutube動画でも解説していますので合わせてチェックしてみてください!
目次
ポアソン回帰とは

ポアソン回帰とは、まれにしか起こらないような現象に関するカウントデータを分析するための手法です。
これは、そのような場合のカウントデータが近似的にポアソン分布に従うという性質を利用しています。
ポアソン分布とは簡単に言うと、ある期間に平均λ回起こるような事象が一定期間にk回発生する確率の分布のことです。
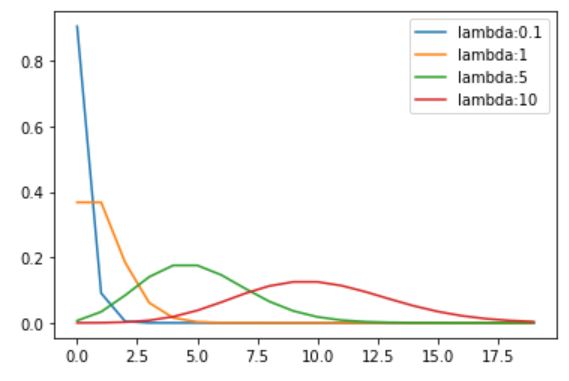
下のグラフは、ポアソン分布のパラメータであるλの値を変化させたときの、分布の形をそれぞれ示しています。
縦軸は確率、横軸はk(確率変数)を表しています。
そうなんです。
実は、λが十分に大きいとき、ポアソン分布は正規分布に近似できるという性質があります。
そのため、目的変数の分布がそのような場合には重回帰分析を適用しても問題ありません。
しかし、例えばλ=1のときをみてみると、右裾が長く、かつ確率変数の値が正であるということがわかります。
これでは目的変数の分布が正規分布であると仮定している重回帰分析は使えませんよね。
そこで、ポアソン回帰分析を用いるというわけです。
ポアソン回帰の理論

ここからはポアソン回帰の理論的な部分を説明していきます。
1. ポアソン回帰モデル
あるカウントデータ\(y_{i}\)が、平均\(\lambda_{i}\)のポアソン分布に従っているとします。
このとき、特定の\(y_{i}\)の値が生じる確率\(P(y_{i}|\lambda_{i})\)は、
\(\displaystyle P(y_{i}|\lambda_{i})=\frac{\lambda^{y_{i}}_{i}\exp(-\lambda_{i})}{y_{i}!}\)
と表すことができます。
ただし、
\(\displaystyle \lambda_{i}=\exp(X^T_{i}\beta)\)
であるとします(\(\lambda_{i}\)は複数の説明変数\(X^T_{i}\)とパラメータ\(\beta\)によって決定する、ということ)。
この式を対数変換すると、
\(\displaystyle \log\lambda_{i}=X^T_{i}\beta\)
となります。
ポアソン回帰では、上記の式に基づき\(\lambda_{i}\)を予測していきます。
つまり、パラメータ\(\beta\)を推定していくというわけです。
2. パラメータ\(\beta\)の推定
続いて、パラメータ\(\beta\)を推定していきます。
ポアソン回帰では、最尤法を用いてパラメータを推定していきます。
同時確率関数\(P(y_{1},y_{2},…,y_{n}|\lambda_{1},\lambda_{2},…,\lambda_{n})\)は
\begin{eqnarray*}
\displaystyle P(y_{1},y_{2},…,y_{n}|\lambda_{1},\lambda_{2},…,\lambda_{n}) &=&\prod_{i=1}^{n} P(y_{i}|\lambda_{i}) \\ &=&\prod_{i=1}^{n} \exp(y_{i}\log\lambda_{i}-\lambda_{i}-\log y_{i}!)\\ &=& \exp\left(\sum_{i=1}^{n}(y_{i}\log\lambda_{i}-\lambda_{i}-\log y_{i}!)\right)\\
\end{eqnarray*}
となるので、対数尤度関数は
\begin{eqnarray*}
\displaystyle \log L(\beta) &=& \log\left(\exp\left(\sum_{i=1}^{n}(y_{i}\log\lambda_{i}-\lambda_{i}-\log y_{i}!)\right)\right) \\ &=& \sum_{i=1}^{n}(y_{i}X^T_{i}\beta-\exp X^T_{i}\beta-\log y_{i}!) \\
\end{eqnarray*}
となります。
この対数尤度関数を\(\beta\)で偏微分していき、推定を行います。
この計算は式で綺麗に求めるのは難しいためニュートン法などの数値計算方法を用いる必要があります。
ポアソン回帰を行う際の注意点

ここで、ポアソン回帰を行う際の注意点を2つ述べておきます。
1. カウントデータ=ポアソン回帰はNG
カウントデータであるからといって、むやみにポアソン回帰を適用させてはいけません。
ポアソン分布は、np=λのままでnを十分大きく、pを十分に小さくした場合の二項分布です。
つまり極限分布ですから、発生数はカウントできるものの、発生率の分母nが不特定多数または非常に膨大で、事実上無限大に近い時によく当てはまります。
例えば地震の発生件数や、飛行機墜落事故の発生件数などがポアソン分布への当てはまりが良いとして知られています。
一方で、医療分野におけるカウントデータ例として、一定時間内に疾患を発症した例数や疾患による死亡例数があります。
これらのカウントデータは、疾患を発症しない例数や疾患によって死亡しない例数を特定することができる、すなわち発生率の分母nを特定することが可能です。
つまり、このようなデータはポアソン分布に近似するとは言えないため、カウントデータではなく出現率や死亡率のデータとして扱い、ロジスティック回帰などを適用する必要があります。
2. ポアソン回帰の制約に注意
上でも述べたように、ポアソン回帰はポアソン分布を仮定した回帰モデルです。
つまり、目的変数の期待値と分散が等しいということを仮定しています(ポアソン分布の性質)。
しかし実際のデータでは、ポアソン分布に従うように見えても、過小分散であったり過分散であったりということがあります。
そのような場合、ポアソン回帰を適用したとしても当てはまりがよくないことがあるので気をつけましょう。
仮に過分散であることがわかった場合には、負の二項分布を仮定した回帰モデルを適用することがあります。
ポアソン回帰の活用例

ここではポアソン回帰の適用例を3つ紹介していきます。
1. 交通データ
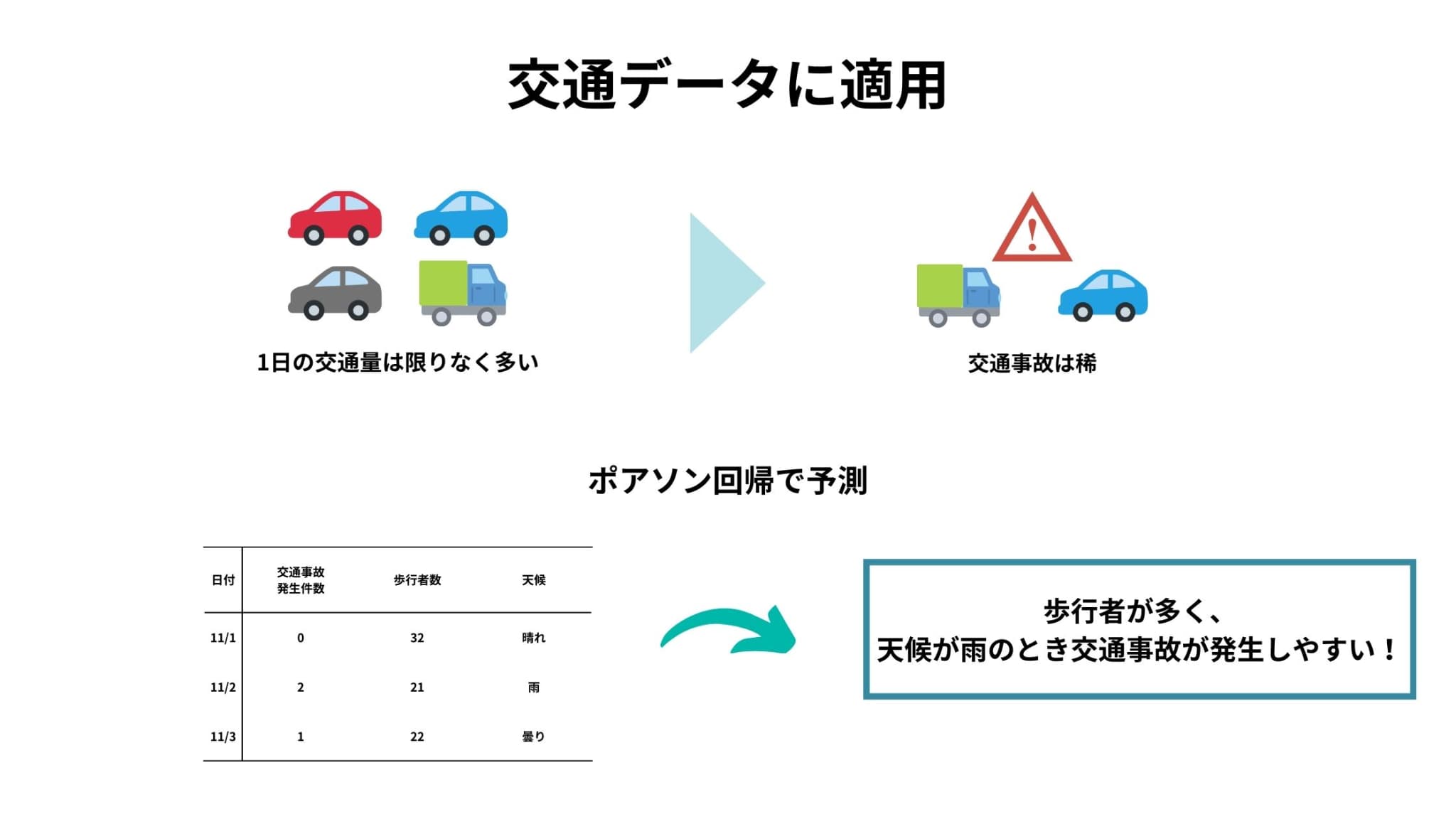
ポアソン回帰がよく適用される例として、交通事故の予測・要因分析があります。
交通事故の発生件数は、母数を一日の交通量と考えるならば稀にしか起こらない現象のカウントデータと考えることができ、大抵の場合ポアソン分布にも従います。
例えば、天候や周囲の交通状況などを説明変数として事故の発生件数を予測するモデルなどがあります。
2. スポーツデータ
スポーツデータに対しても、ポアソン回帰を用いることがあります。
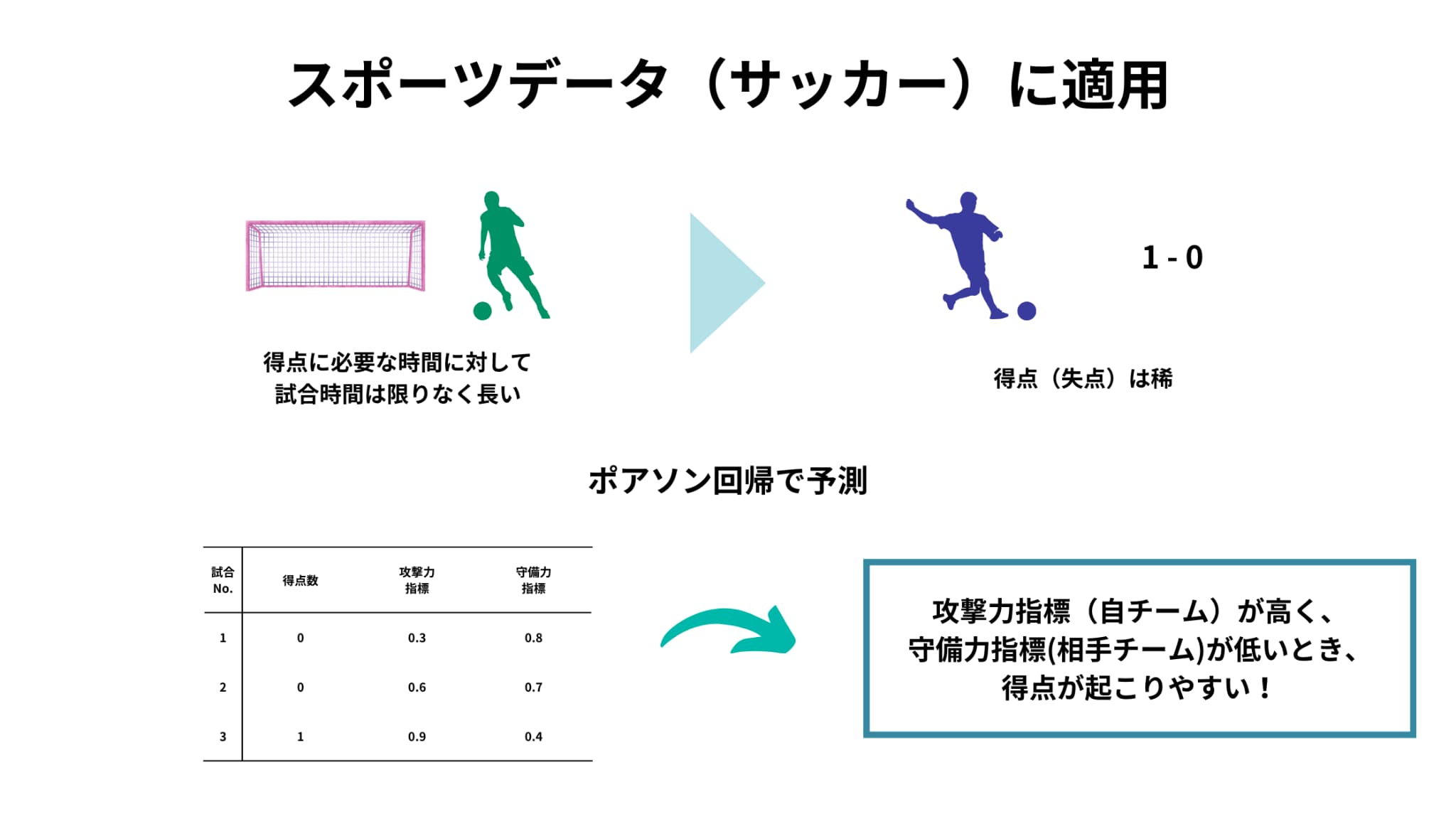
特に有名なのが、サッカーの得失点の予測。
サッカーは得失点の少ないスポーツです。得点が決まる最小単位の時間を10秒と考えると、試合時間90分はそれに対して非常に長いです。つまり、サッカーにおける得失点は稀にしか起こらない現象のカウントデータと考えることができ、ポアソン分布への当てはまりが良い事例として知られています。
例えば、攻撃力や守備力を表す指標を説明変数として得失点を予測するモデルなどがあります。
他にも、野球におけるヒット数やホームラン数などもポアソン分布への当てはまりが良い場合があります。
3. 購買データ
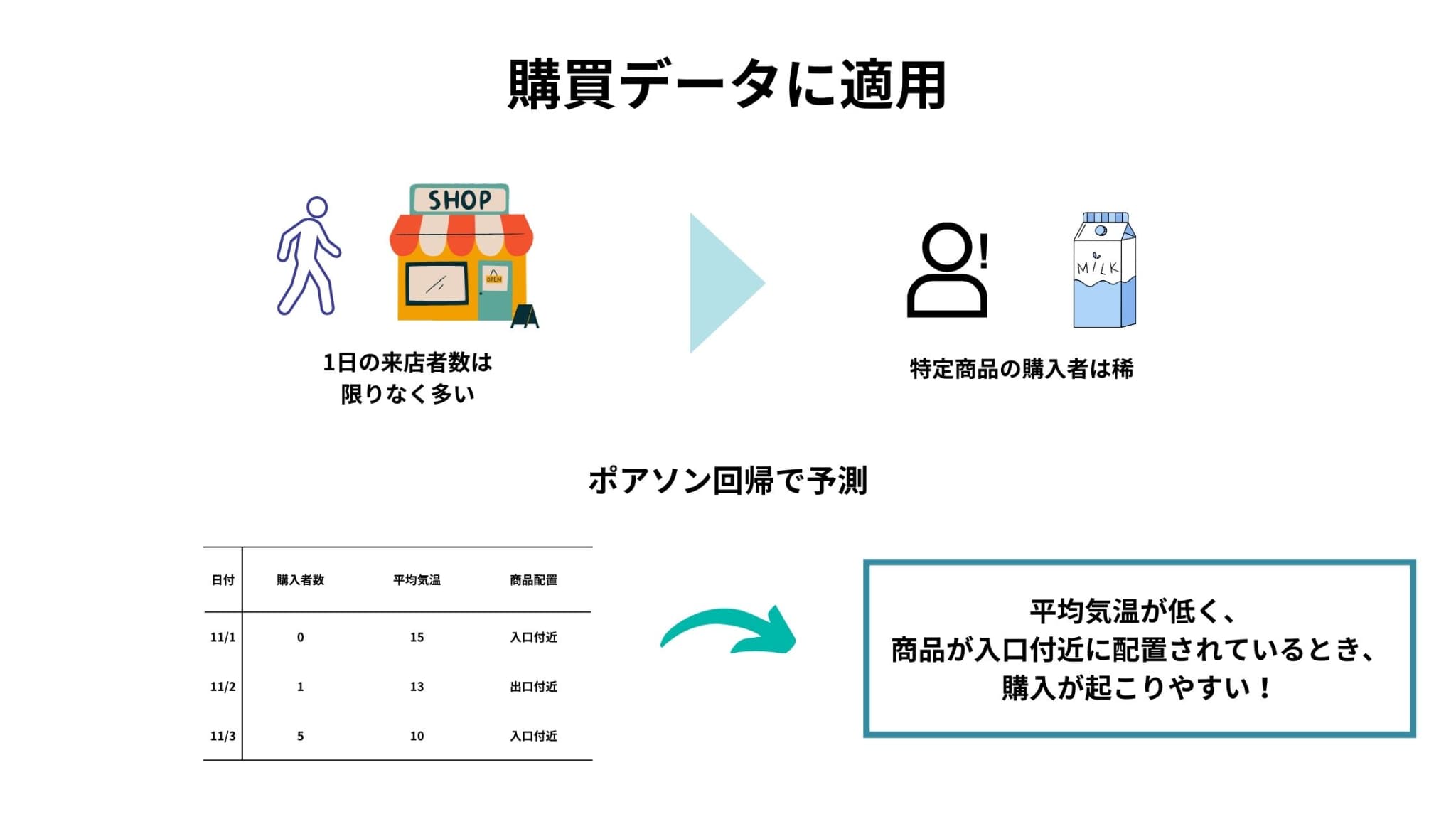
購買データに対しても、ポアソン回帰を用いることがあります。
例えば、ある商品の購入者数。
ある商品の購入者数は、母数を来店者数と考えるならば稀にしか起こらない現象のカウントデータと考えることができ、ポアソン分布への当てはまりが良い場合があります。
この場合、日付ごとの天候や商品の配置場所を説明変数として購入者数を予測するモデルなどが考えられます。
ポアソン回帰をPythonでやってみよう

ここからは、Pythonで実際にポアソン回帰をやっていきます!
同時に通常の重回帰分析も行い、どちらの予測精度の方が良いかを確認します。
以下の流れで分析を進めていきます。
1. ライブラリのインストール
2. データの準備
3. 分析の準備
4. ポアソン回帰の実行
5. モデルの評価
1. ライブラリのインストール
今回はsklearnのPoissonRegressorを使ってポアソン回帰を行っていきます。
分析で使用する他のモジュール等もここで全てimportしておきます
#モジュール等のインポート
import urllib
from urllib import request
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import PoissonRegressor
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error2. データの準備
今回はポルトガルの公立高校の生徒の成績データを使っていきます。
2005年から2006年の実データ(N = 649)で、家庭環境や欠席傾向に関するデータが格納されています。
#データの準備
url = 'https://raw.githubusercontent.com/okeefj22/CA4010-data-project/master/datasets/student-por.csv'
data_path = 'data.csv'
urllib.request.urlretrieve(url, data_path)
#データの読み込み
df = pd.read_csv('data.csv')
df.head(5)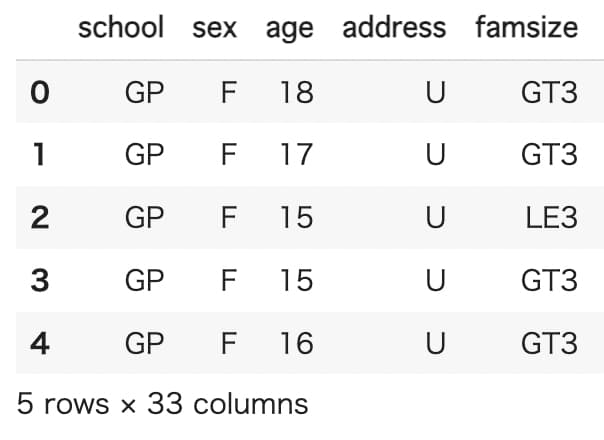
3. 分析の準備
今回は1年間の欠席の回数(absences)を目的変数として分析を行っていきます。
目的変数のヒストグラムがこちら。
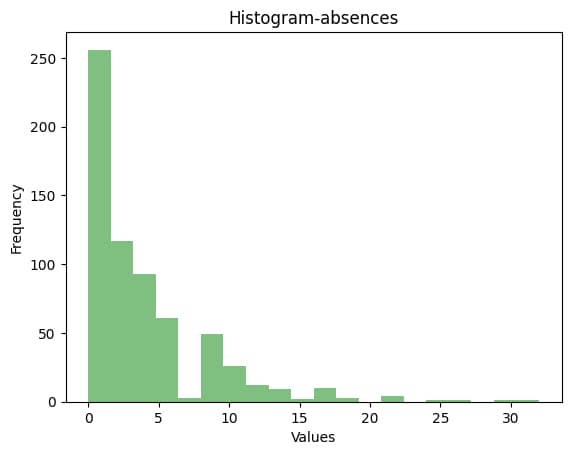
右裾が長い分布となっており、正規分布よりもポアソン分布に近い形になっていることがわかります。
続いて、分析に使うデータを選択し、学習データとテストデータに分けていきます。
特徴量として、性別(sex)、年齢(age)、住所(address)、父親の学歴(Fedu)、勉強時間(studytime)、家族との関係性(famrel)を使用します。
#使用する変数のみのデータフレームを作成
data_df = df[['sex','age','address','Fedu','studytime','famrel','absences']]
#カテゴリ変数のダミー変数化
data_df = pd.get_dummies(data_df, drop_first=True)
#特徴量と目的変数に分ける
X = data_df.drop('absences', axis=1) #特徴量
y = data_df['absences'] # 目的変数
# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 分割後のデータのサイズを確認
print("Training data size:", X_train.shape, y_train.shape)
print("Testing data size:", X_test.shape, y_test.shape)4. ポアソン回帰の実行
学習データを使って回帰モデルを作成し、テストデータを使ってその精度を確認します。
なお、比較のため、重回帰分析も行います。
#ポアソン回帰の実行
pr = PoissonRegressor()
pr.fit(X_train, y_train)
y_pr_predict = pr.predict(X_test)
#重回帰分析の実行
lr = LinearRegression()
lr.fit(X_train, y_train)
y_lr_predict = lr.predict(X_test)5. モデルの評価
両者のモデルの評価はMSE(平均二乗誤差)を用いて行います。
MSEとはその名の通り、予測値と正解値の差の二乗の平均のことです。
値が小さいほど誤差の少ない良いモデルと言えます。
#モデルの評価
evaluation = pd.DataFrame()
evaluation.loc['Poisson Regression', 'mse'] = mean_squared_error(y_test, y_pr_predict)
evaluation.loc['Linear Regression', 'mse'] = mean_squared_error(y_test, y_lr_predict)
evaluation
若干ですが、ポアソン回帰のMSEの方が小さくなりました。
つまり、ポアソン回帰の方が当てはまりの良いモデル(予測精度が高い)と言えます。
特徴量選択をより丁寧に行えば、さらに良い結果が得られるでしょう。
まとめ
ここまでご覧いただきありがとうございました!
本記事ではポアソン回帰の概要からPythonでの実装方法まで解説していきました。
近年は様々な機械学習手法が発展してきたこともあり、変数の分布も特に考慮せず分析を始めがちですが、しっかりと分布を確認することでより良い結果が得られることが多々あります。
手元のデータを分析する場合、分布を確認し、最適な分析手法を選択するということを心がけていきましょう!
また、今回分析に用いたPythonについて勉強したい方は以下の記事を参考にしてみてください!

さらに詳しくAIやデータサイエンスの勉強がしたい!という方は当サイト「スタビジ」が提供するスタビジアカデミーというサービスで体系的に学ぶことが可能ですので是非参考にしてみてください!
AIデータサイエンス特化スクール「スタアカ」

| 【価格】 | ライトプラン:1280円/月 プレミアムプラン:149,800円 |
|---|---|
| 【オススメ度】 | |
| 【サポート体制】 | |
| 【受講形式】 | オンライン形式 |
| 【学習範囲】 | データサイエンスを網羅的に学ぶ 実践的なビジネスフレームワークを学ぶ SQLとPythonを組み合わせて実データを使った様々なワークを行う マーケティングの実行プラン策定 マーケティングとデータ分析の掛け合わせで集客マネタイズ |
データサイエンティストとしての自分の経験をふまえてエッセンスを詰め込んだのがこちらのスタビジアカデミー、略して「スタアカ」!!
当メディアが運営するスクールです。
24時間以内の質問対応と現役データサイエンティストによる複数回のメンタリングを実施します!
カリキュラム自体は、他のスクールと比較して圧倒的に良い自信があるのでぜひ受講してみてください!
他のスクールのカリキュラムはPythonでの機械学習実装だけに焦点が当たっているものが多く、実務に即した内容になっていないものが多いです。
そんな課題感に対して、実務で使うことの多いSQLや機械学習のビジネス導入プロセスの理解なども合わせて学べるボリューム満点のコースになっています!
Pythonが初めての人でも学べるようなカリキュラムにしておりますので是非チェックしてみてください!
ウォルマートのデータを使って商品の予測分析をしたり、実務で使うことの多いGoogleプロダクトのBigQueryを使って投球分析をしたり、データサイエンティストに必要なビジネス・マーケティングの基礎を学んでマーケティングプランを作ってもらったり・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践してもらったりする盛りだくさんの内容になってます!
・BigQuery上でSQL、Google Colab上でPythonを使い野球の投球分析
・世界最大手小売企業のウォルマートの実データを用いた需要予測
・ビジネス・マーケティングの基礎を学んで実際の企業を題材にしたマーケティングプランの策定
・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践して稼ぐ