【5分でわかりやすく解説】k-means法とは?RとPythonで実装してみよう!
こんにちは!
データサイエンティストのウマたん(@statistics1012)です!
大学院時代は、クラスター分析を用いて回帰分析の精度を高める手法の研究などを行っていました。
クラスター分析は非常に便利な手法でビジネスの場でもよく使われます。

そんなクラスター分析には実は階層的クラスター分析と非階層的クラスター分析があるということをご存知でしょうか?
階層的クラスター分析は分かりやすく、結果が出た後に分類の様子からクラスタ数を決めることが可能です。
ただデータ量が多くなると計算に時間がかかるというデメリットがあります。
一方非階層的クラスター分析は、クラスタ数をあらかじめ決めておかなくてはいけませんが膨大なデータでも比較的計算が早く終わるというメリットがあります。
どちらの手法も一長一短ですが、一般的にビジネスの場では膨大なデータを扱うことが多いため非階層的クラスター分析が良く用いられます。
この記事では、そんな非階層的クラスター分析の中で最もよく用いられるk-means法についてまとめていきます。
k-means法を進化させたx-means法についても紹介していきますので是非参考に!
・k-means法のメリット
・k-means法のデメリット
・k-means法のデメリットを解消した最強の手法「x-means法」
・k-means法とx-means法をRで実装してみよう!
・k-means法をPythonで実装してみよう!
以下の動画でも分かりやすく解説しているので是非チェックしてみてください!
目次
k-means法とは

まず、初めにk-means法とは何か見ていきましょう!
1.代表点を適当に決める
2.ユークリッド距離をもとにデータを代表点を持つクラスタに割り当て
3.クラスタの重心点を代表点とする
4.代表点が変わらなければ終了。変われば2へ
具体的にk-means法がどういうフローを取るのか図で見ていきます。
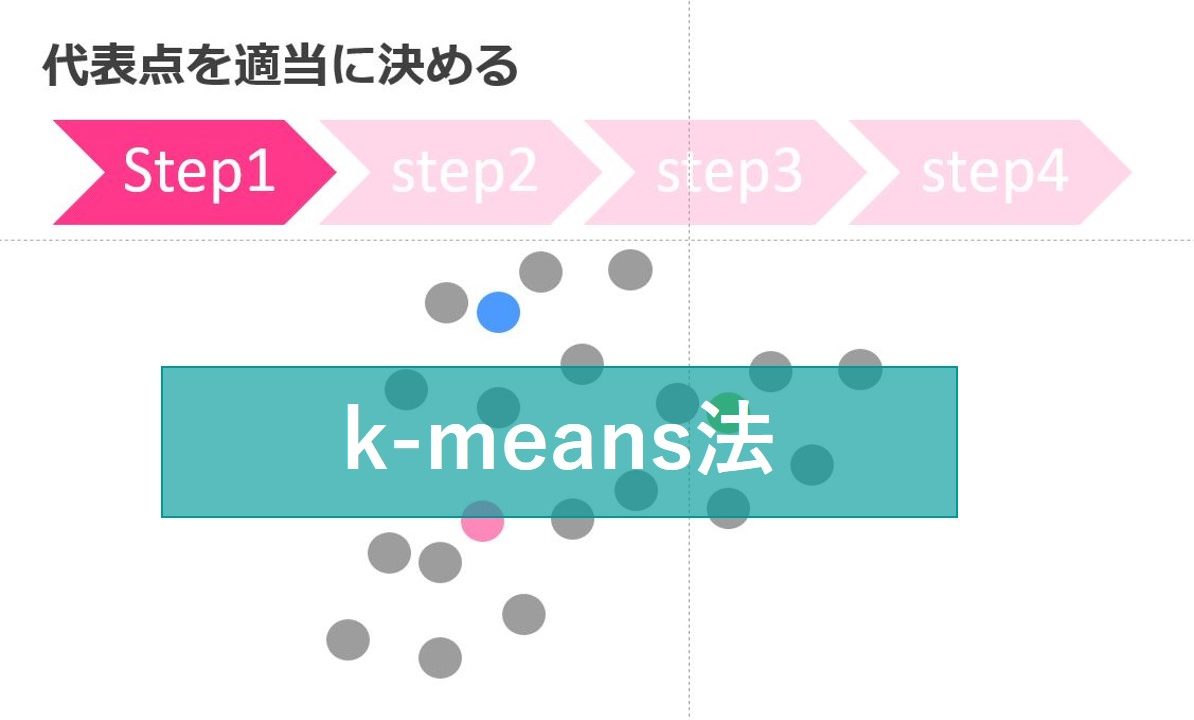
代表点を決める
まず代表点を適当に決めます。
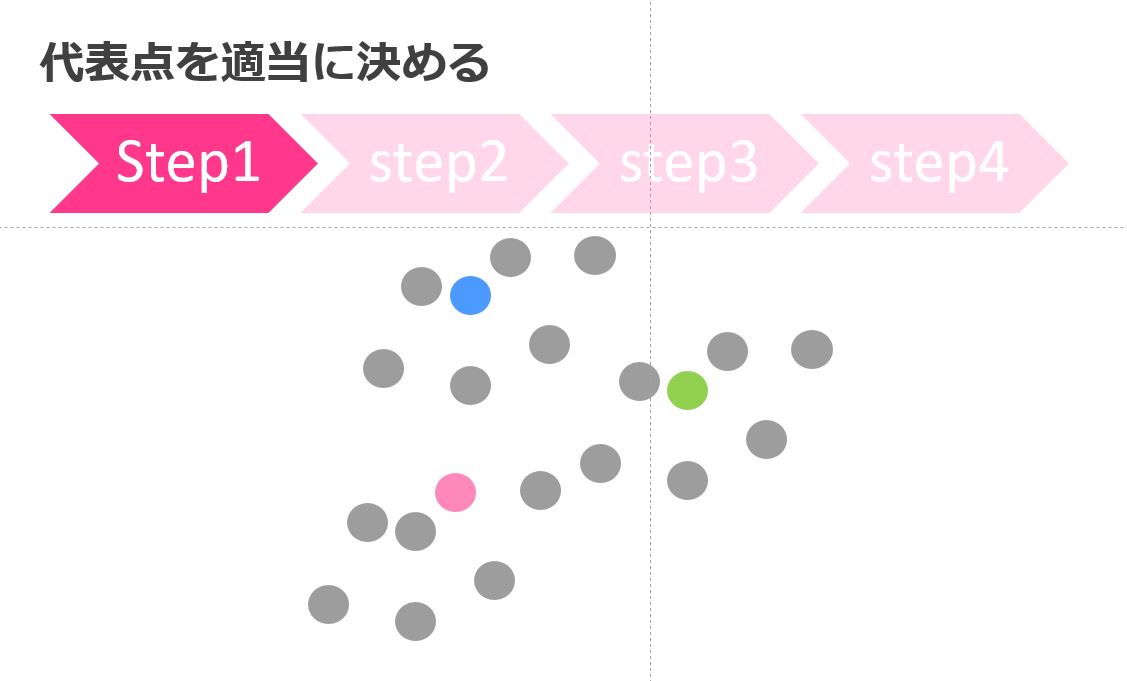
この際にクラスタが3つなら3つの代表点が選ばれます。
クラスタに分ける
続いてStep2、ユークリッド距離を計算して各データはどの代表点に近いかでグループ分けします。
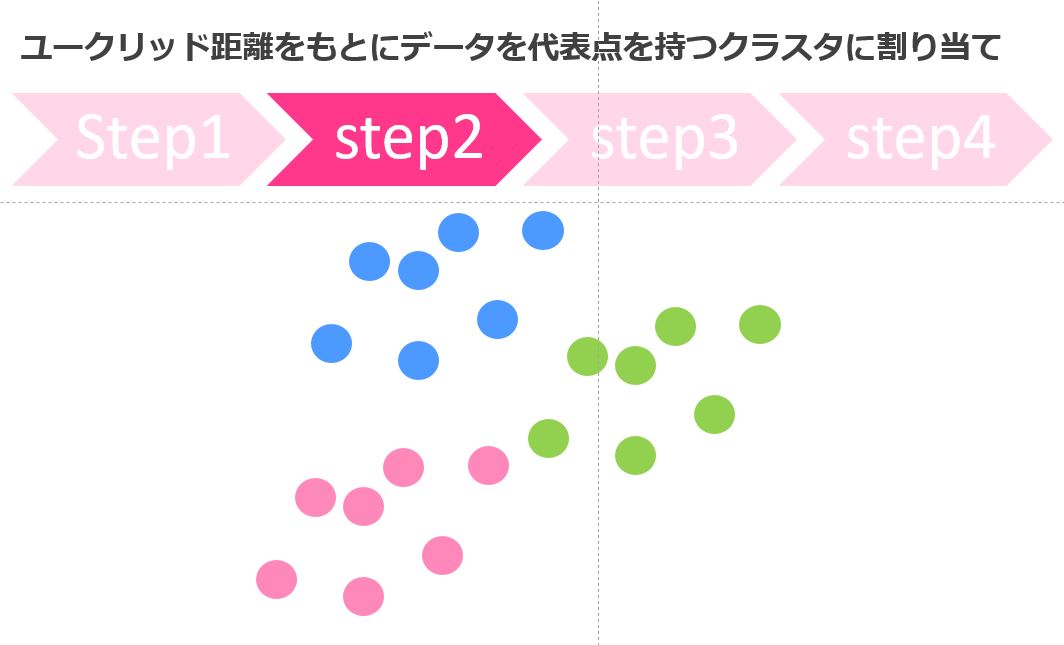
最初の適当な点が今回は比較的良かったので綺麗に分かれていますが、毎回そうとは限りません。
重心点を計算する
続いてStep3、各クラスタの重心点を計算します。
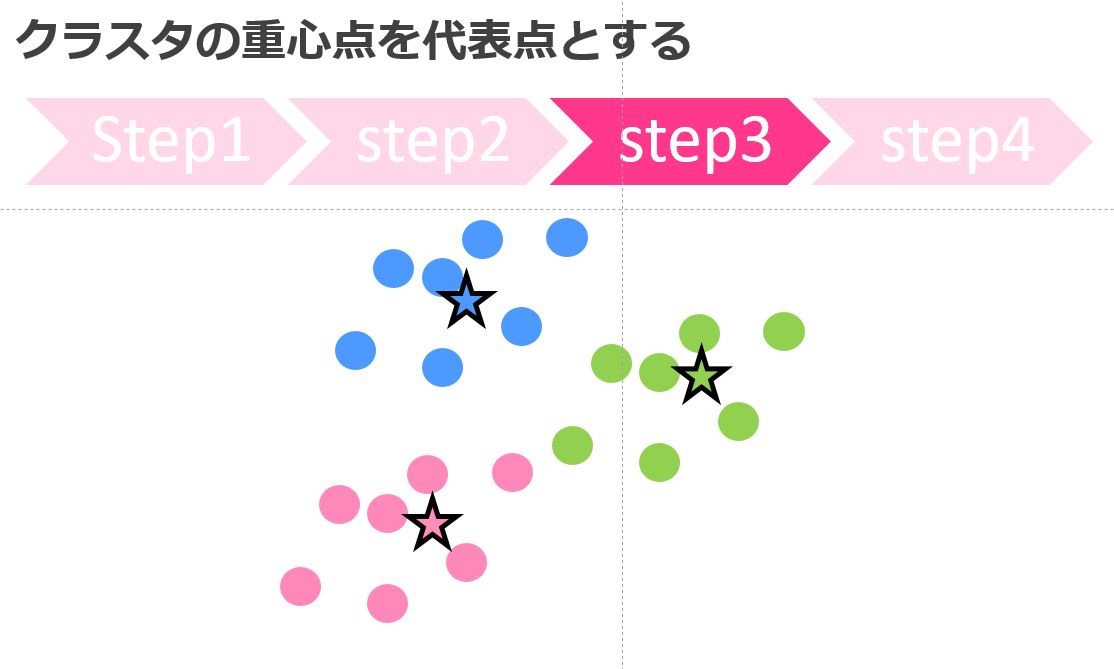 このクラスタの重心点が次の代表点になります。
このクラスタの重心点が次の代表点になります。
クラスタを再分類
そしてまたStep2に戻って・・・を繰り返して最終的に代表点が動かなくなったら終了!
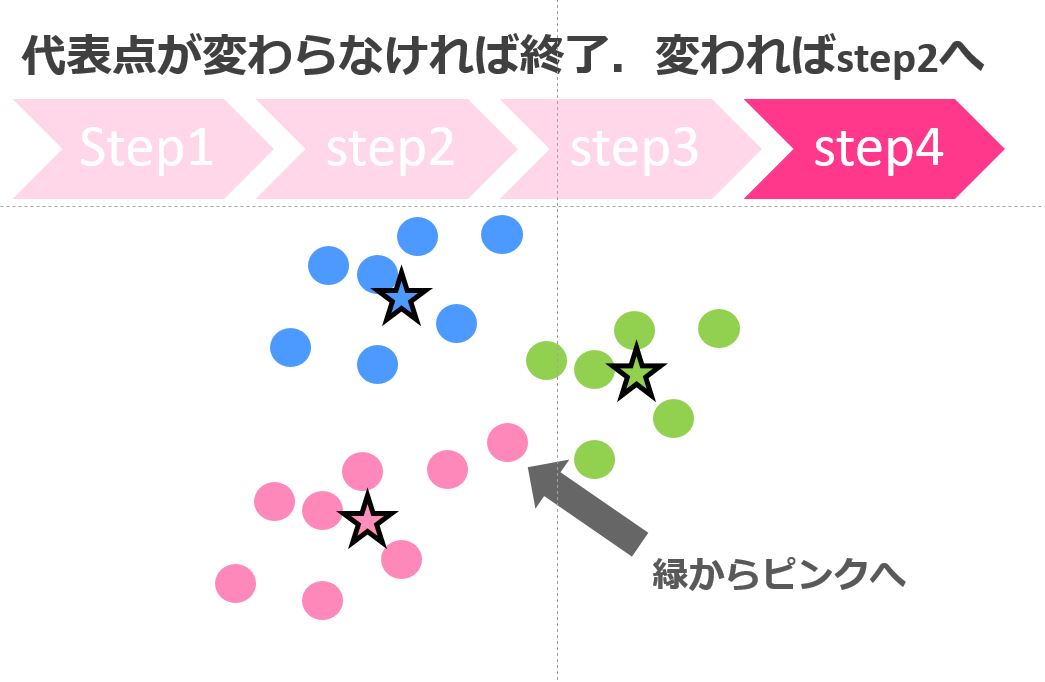
今回は緑の〇が一つピンクになりました。
※イメージしやすいように手で作っているので少し違和感あるかも
非常に単純なアルゴリズムなんです。
k-means法のメリット

そんなk-means法ですが、どんなメリットがあるのでしょうか?
アルゴリズムが単純で分かりやすい
k-means法のアルゴリズムは図で考えると非常に単純で分かりやすいんです。
アルゴリズムを覚える必要はありませんが、ある程度説明できるのと説明できないのとでは説得力が違います。
計算負荷が少ない
アルゴリズムが単純であることと関連するのですが、その分計算負荷が少ないので膨大なデータに対しても素早く計算することが可能です。
そのため、大量のデータを扱うことの多いビジネスの場ではk-means法が好んで使用されます。
k-means法のデメリット

ただ、一方でk-means法のデメリットも存在します。
クラスタ数をあらかじめ決めなくてはいけない
先ほども書きましたが、k-means法はクラスタ数をあらかじめ決めなくてはいけません。
クラスタ数をいくつか動かしてみて最も最適なクラスタ数を探すと良いでしょう。
クラスタに意味を与えるのがマーケターの仕事なのです。
ちなみに自動で最適なクラスタ数を算出してくれる「x-means法」という手法もありますので後で見ていきましょう!
局所最適解になってしまう
代表点を決めてそこから逐次的に最適解を探していくため、局所最適になってしまい、大局的最適解であるとは限りません。
そのため代表点の選び方によって結果が変わることがあります。
k-means法とk近傍法の違い
k-means法と名前の似ている手法にk近傍法という手法があります。
これらの手法、実は全然違うんです!!笑
k-means法は教師なし学習であるのに対してk近傍法は教師あり学習!
k近傍法は周りの教師データから未知データのラベルを判別する分類系の機械学習手法です。
そしてkとは手法に与えるパラメーターで、近くに存在する学習データのクラス数を示しています。
たとえば、このような状況では
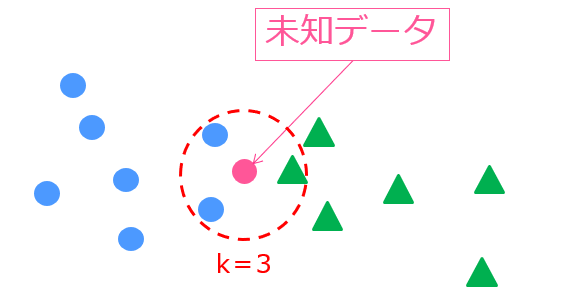
k=3なので未知データの周りの3つのデータを判断材料とします。
実際に見てみると、青〇のクラスが2つ、緑△のクラスが1つなので、未知データは青〇と判断されます。
詳しくは以下の記事でまとめているのでご覧ください!

k-means法のデメリットを解消した最強の手法「x-means法」

実はk-means法のデメリットを解消した「x-means法」という手法があるんです。
「x-means法」を使えば、最適なクラスタ数を自動で決めてくれます。
「x-means法」はPelleg and Moore(2000)によって名づけられたもので,始めに十分に小さなクラスタ分割から始めて、各クラスタについて2分割が適当であると判断される限り分割を繰り返すものです。
アルゴリズムは以下。
1.クラスタ数をnとしk-means法を行う。⇛C1,C2,…Cn
2.Ci(i=1,2,…,n)にクラスタ数を2としk-means法を行う。
3.分割前のBIC (ベイズ情報量基準)と分割後のBICを比較し大きくなるならその分割をし,そうでないなら分割しない。
4.2,3を分割できるクラスタがなくなるまで繰り返す。
BICはある種の回帰分析の変数選択の場面で用いられることがある、サンプル数をペナルティ項として課した指標です。
AIC(赤池情報量基準)などと仲間です。
この時、BICの式を簡単に書くと以下のようになります。
BIC=ー(尤度)+k×(サンプル数)
サンプル数が大きければ大きいほどBICは大きくなり、尤度が小さければ小さいほどBICが大きくなります。
今回のケースでは、クラスタ内多変量正規分布のばらつきが小さいほど尤度は小さくなります。
そのため、サンプルが多くてかつばらつきが少ないクラスターができるとBICが大きくなるというイメージ。
そのロジックを使って、BICが大きくなるのであれば分割するというようなアルゴリズムになっているのがこのx-means法なのです。
これだけ聞くとx-means法の方が良さそうですが、k-means法は元々局所最適解に陥りやすいのにもかかわらずx-means法はさらに局所最適解に陥りやすくなっています。
簡易的に計算する分にはx-means法を使ってもよいかもしれませんが、最適なクラスタ数を精緻に探す場合はk-means法のほうが良いかもしれません。
詳しくは以下の論文(石岡[2000])を読んでいただくと良いと思います。
k-means法とx-means法をRで実装してみよう!

それでは、最後にk-means法とx-means法をそれぞれRで実装していきましょう!
Rのパッケージ内に入っているk-means法と先ほどの石岡[2000]の論文中のx-means法を使って比較してみます。
(x-means法はパッケージがないので別途実装が必要ですが、ネットにソースが落ちています)
データは、irisというめちゃんこ有名なR内のデータセット(150サンプル5変数で花びらの特徴を表したデータセット)を使います。
3つの花のタイプに分かれているので、そのラベルがk-means法とx-means法で上手く分類できるかどうか見ていきます。
実際に行ってみた結果がこちら
■k-means法
| 1 | 2 | 3 | |
| setosa | 0 | 50 | 0 |
| versicolor | 48 | 0 | 2 |
| virginica | 14 | 0 | 36 |
■x-means法
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| setosa | 28 | 22 | 0 | 0 | 0 | 0 | 0 | 0 |
| versicolor | 0 | 0 | 18 | 4 | 6 | 20 | 0 | 2 |
| virginica | 0 | 0 | 1 | 13 | 0 | 0 | 12 | 24 |
k-means法は明示的にクラスタ数を3と指定しているのでそれなりに綺麗にクラスタが分かれていますが、x-mean法ではクラスタ数が8つに分かれてしまっています・・・
x-means法は非常に便利な手法ですが、気を付けて使わないといけないですね。
k-means法をPythonで実装してみよう!

k-means法は、RでもできますしもちろんPythonでも実装できちゃいます!
同じくirisデータを分類してみましょう!
やっていることはRと変わりません。
正答率は88%になりました!
RもPythonもk-means法を行う分にはそれほど変わりませんが、Pythonの方ができることの幅が広いのでPythonに慣れておくことをオススメします!

Pythonの勉強方法については以下にまとめていますので参考にしてみてください!

k-means法をビジネスで活かす場面

さて、k-means法の種類や仕組み・そしてRでの実装について分かったところでどのようにビジネスに活かしていけばよいのか見ていきましょう!
ここでは2つの観点でk-means法の使いどころを見ていきます。
・セグメントの可視化
・教師あり学習の特徴量生成
セグメントの可視化
もう既にお分かりの通り、k-means法を使えばお客さんの行動データや属性データを基にいくつかのセグメントに分けることができます。
あるセグメントは、年配の女性で購入金額が高い層
もう一方のセグメントは、若い男性で購入金額が低い層、などが考えれます。
この2つのセグメントに対して行うコミュニケーションは変えるべきだということが分かりますね。
このように、セグメントの可視化を行いセグメントのユーザー像を明確にすることで、マーケティング活動を効率化することが可能になります。
このセグメントの可視化においてユーザー像を想像するのはマーケターの腕の見せ所で、クラスター数を変化させてどのようなセグメント定義であれば最適なコミュニケーション設計ができるのか考えていくことになります。
教師あり学習の特徴量生成

先ほども紹介しましたが、教師あり学習というのは正解が紐づいているデータを学習する手法のことを指しましたね。
教師あり学習を使うと、過去の顧客の購買という正解データから未来の購買を予測することが可能です。
そんな、顧客の購買を予測するときにクラスター分析で得られたクラスターを特徴量として新たに追加して使うことがあります。
これによりインプットされるデータがリッチになって、他の特徴量で表現できなかったことが表現できるようになる可能性があります。
つまりk-means法によって生成された特徴量を使って顧客の購買予測精度の向上が見込めるんです。
特徴量に関するテクニックは以下の記事で詳しくまとめています!

効果が本当に見込めるかどうかはデータによりますが、精度を向上させる手段として覚えておくとよいでしょう!
1つ目の可視化に関しては現状を把握することに重きが置かれていましたが、2つ目では予測の精度を高めるための1つの情報として使われました。
どちらもやっていることはさほど変わらないのですが、k-means法には色々な使い方があるということは理解しておきましょう。
k-means法 まとめ
ここまでご覧いただきありがとうございました!
本記事では、k-mean法をメインに見てきました。
最後にk-means法についてまとめておきましょう!
■k-means法のメリット
・計算負荷が少ない
・アルゴリズムが単純で説明しやすい
■k-means法のデメリット
・クラスタ数をあらかじめ決めなくてはいけない
・局所最適解に陥りやすい
k-mean法はとても優秀で汎用性の高い手法であり、様々なビジネスシーンで使われます。
是非使ってみてください!
ちなみに階層的クラスター分析に関してもっと詳しく知りたい方は以下の記事を参考にしてみてください。

また機械学習やデータサイエンスについてもっと詳しく知りたい方はぜひ以下の記事を参考にしてみてください!


当メディアでは、k-meansを含めた様々な機械学習手法やデータサイエンスの知識を体系的に学べるスタアカ(スタビジアカデミー)というスクールを展開していますので是非チェックしてみてください!






















