【5分でわかりやすく解説】k近傍法とは?理論とRでの実装方法!

こんにちは!
データサイエンティストのウマたん(@statistics1012)です!
アルゴリズムが分かりやすくて使いやすい手法であるk近傍法!
この記事ではそんなk近傍法というクラス判別の手法をご説明します!
アルゴリズムも非常に分かりやすく使いやすいk近傍法についてみていきましょう!
最後にはRでの実装方法も見ていきますよー!
他の手法についてはこちらも合わせてご参照ください!


k近傍法とは

それではk近傍法の解説からはじめましょう!
以下の動画でも解説しているのでぜひチェックしてみてください!
k近傍法とはデータを分類する時に活躍する手法です。
ある未知データが与えられたとき、周りの学習データのクラスからその未知データの分類を決定するもの。
そしてkとは手法に与えるパラメーターで、近くに存在する学習データのクラス数を示しています。
たとえば、このような状況では、
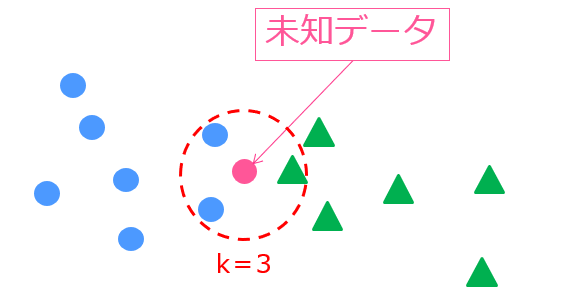
k=3なので未知データの周りの3つのデータを判断材料とします。
実際に見てみると、青〇のクラスが2つ、緑△のクラスが1つなので、未知データは青〇と判断されます。
続いてこのkを5にするとどうなるでしょう?
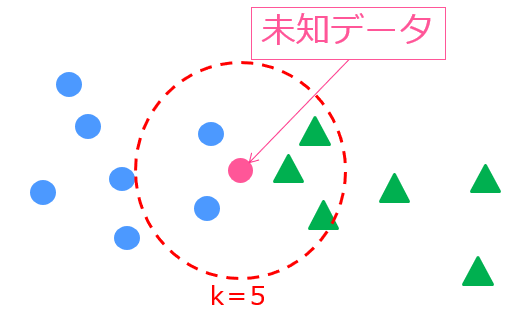
k=5なので周りの5個を判断材料とします。
実際に見てみると、青〇のクラスが2つ、緑△のクラスが3つなので、未知データは緑△と判断されます。
kの値を変えることで分類されるクラスが変わりましたね!
今回挙げた例は非常に分類が難しい例であり、このような場合はそれほど多くありませんがkの値によって分類されるクラスが変わる可能性はあるよ!というお話でした。
ちなみにRで解析する時はclassパッケージのknnという関数を使うと良いでしょう!
この時デフォルトではk=1になっています。すなわちこれは、近くの1つしか判断材料に入れないということ。
これは最近傍法というk近傍法の特殊な例になってしまい局所最適に陥りやすいです。
あまりにも大きすぎるkの値は不均衡データに対して上手く分類できなくなってしまう可能性もありますが、ある程度大きい値にした方が良いでしょう!
個人的には5が推奨です。解析の時は大抵5を選択していました。
実はこのk近傍法の考え方を不均衡データに応用したSMOTEという方法があります。
k近傍法の識別規則

それでは、具体的にk近傍法の識別規則について数式で見ていきましょう!
\begin{eqnarray}
\left\{
\begin{array}{l}
j&…&((k_j)=max(k_1,…,k_K)の時)\\
reject&…&((k_1,…,k_j)=max(k_1,…,k_K)の時)\\
\end{array}
\right.
\end{eqnarray}
非常に簡単な数式になりました!
この時\(k_i\)は近傍kのうち、クラスiに属するデータ数を表しています。
近傍kの中でも最もクラスjに属するデータが多いときそのデータをjと識別します。
最もデータ数が多いクラスが多数存在する場合は識別不能となります。
k近傍法は非常に分かりやすいアルゴリズムなのでとっかかりやすいです!
Rのパッケージで一発で出来ちゃうんで使ってみましょう!
ちなみにk近傍法と名前の似ている手法にk-means法という機械学習手法があります。
名前は似ていても手法は全く違います!k-means法は教師なし学習でありクラスター分析の一種!
k-means法については以下の記事でまとめているのでよければご覧ください!
k近傍法をRで実装!

k近傍法はRやPythonで簡単に実装することができます。実際にRを用いてk近傍法を実装してみましょう!
今回は、Kaggleの公式サイトで提供されているTitanicのデータを使います。
kaggleに関しては以下の記事で詳しく解説しているのであわせてチェックしてみてください。
データのクレンジングを行い、欠損値は削除、不要と考えられる項目は削除します。
生死(Survive)を目的変数としそれ以外を説明変数とします。
サンプル数714のうちランダムに400個のデータを取り出し学習データとし、残りの314を予測データとします。
学習データで予測モデルを作り、予測データにあてはめ真値と予測値の判別率を精度として比較します。
シミュレーション回数は10回とし、上記の手順を10回繰り返し、結果を平均したものを最終アウトプットとします。
k近傍法をXGboost、ランダムフォレスト、サポートベクターマシン、ナイーブベイズ、ニューラルネットワークの5手法と比較します!他の手法については他の記事をご覧ください。
classというパッケージに入っているknnという関数を用います。
他の手法では大丈夫なんですが、knnは文字列として入っている質的変数を数値に直さなくてはいけないのでこのような処理を施しています。
titanic[,4]<-as.numeric(titanic[,4])
titanic[,9]<-as.numeric(titanic[,9])関数knnでは学習データと未知データと目的変数を与えます。データによっては、パラメータkで精度が大きく変わる可能性があります。
#k-nn
knn<-knn(train.data,test.data,train.data[,"Survived"] ,prob=T,k=3)
test.data.knn<-cbind(test.data,"predict"=knn)
result[i,6]<-sum(test.data.knn$predict==test.data.knn$Survived)/nrow(test.data.knn)結果は以下のようになりました。やはりk近傍法が最も精度が低い・・・
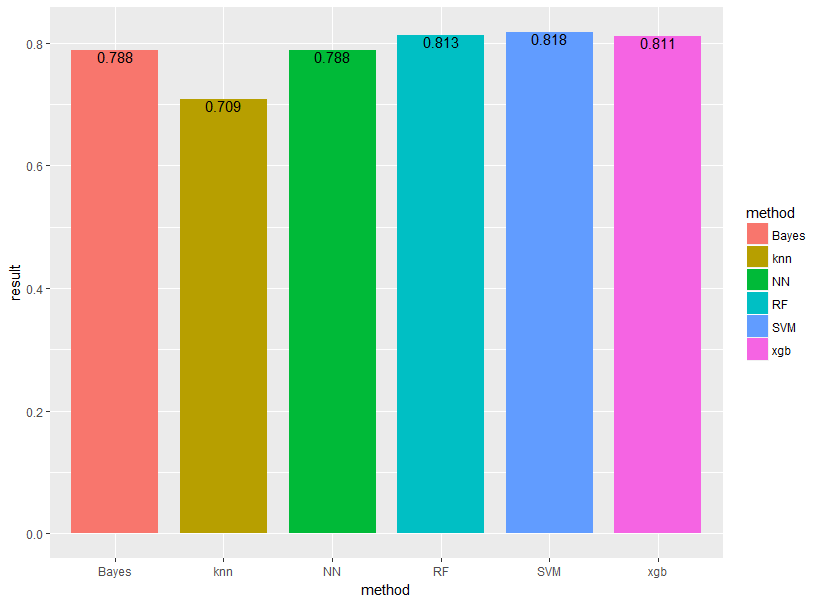
他の機械学習手法に比べるとアルゴリズムが非常にシンプルなのでしょうがない!
k近傍法 まとめ
本記事では、k近傍法について見てきました。
k近傍法はアルゴリズムがシンプルで分かりやすく、精度も比較的高いのでビジネスシーンでも用いられることが多いです。
是非k近傍法を使ってみてください。
ちなみにk近傍法に関しては、機械学習の王道本「はじめてのパターン認識」で取り上げていますのでそちらを読んで理解を深めると良いでしょう!
もし機械学習手法について理解を深めたいのであれば以下の記事を参考にしてみてください!

また、機械学習の勉強やデータサイエンスの勉強については以下の記事で詳しく解説しています!