機械学習の分類・予測精度における評価指標を徹底解説!

こんにちは!
データサイエンティストのウマたん(@statistics1012)です!
ビジネス貢献の生まれる機械学習手法を実装するためには正しく評価をすることが非常に重要です。
CRISP-DMというデータ分析プロセスのフローにおいてもEvaluationはModelingの後のフェーズになっており、ここを間違えると初期のビジネス理解に戻ってしまっています。
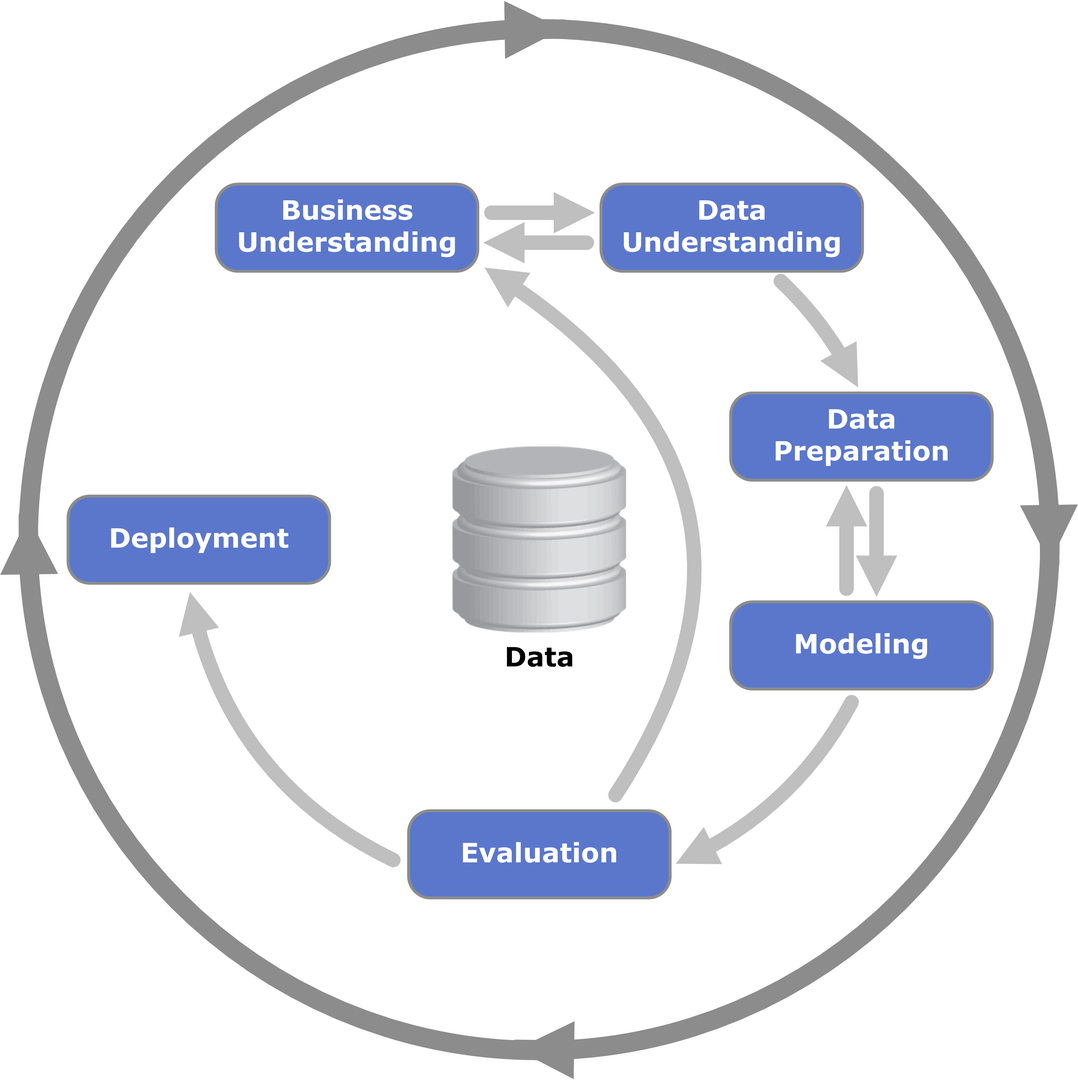
(出典:Wikipedia-‘Cross-industry standard process for data mining’)
正しい評価方法を知らないと、机上検証ではよい評価を算出していたとしても、実際に運用に載せた時に全く事業貢献しないモデルを生み出してしまうかもしれません。
ここでは、ビジネス観点で本当に正しい機械学習モデル構築・データ分析の評価方法について見ていきましょう!
機械学習における評価指標については以下のYoutube動画でも解説していますので是非チェックしてみてください!
目次
機械学習における評価指標の種類

まずは、モデルを評価する上でどのような評価指標があるのか確認しておきましょう!
評価指標には様々な指標があります。
回帰タスクにおける予測精度であれば、
MAE
MSE
RMSE
決定係数(寄与率)
などを用いることが一般的です。
分類タスクにおける分類精度であれば、
正解率
適合率
再現率
F-mesure
などが一般的です。
それぞれについて詳しく見ていきましょう!
予測精度:MAE

回帰タスクとは売上などの量的変数を予測する課題のことです。
まずは、MAE(絶対平均誤差)。
Mean Absolute Errorの略でMAEと呼ばれます。
その名の通り、予測値\(\hat{y_i}\)と実測値\(y_i\)の絶対値の誤差の平均がMAEになり以下の式で表されます。
$$ MAE=\frac{1}{n}\sum_{i=1}^n|\hat{y_i}-y_i| $$
予測精度:MSE
続いてMSE(平均二乗誤差)。
Mean Square Errorの略でMSEと呼ばれます。
その名の通り、予測値\(\hat{y_i}\)と実測値\(y_i\)の誤差を二乗したものを平均したものがMSEになります。
$$ MSE=\frac{1}{n}\sum_{i=1}^n(\hat{y_i}-y_i)^2 $$
予測精度:RMSE
続いてRMSE(平均平方二乗誤差)。
Root Mean Square Errorの略でRMSEと呼ばれます。
その名の通り、予測値\(\hat{y_i}\)と実測値\(y_i\)の誤差を二乗したものを平均して平方根と取ったものがRMSEになります。
先ほどのMSEの平方根を取った指標です。
$$ RMSE=\sqrt{\frac{1}{n}\sum_{i=1}^n(\hat{y_i}-y_i)^2} $$
各種評価指標のPython実装に関しては以下の記事でまとめていますのでチェックしてみてください!

予測精度:決定係数(寄与率)
続いて決定係数(寄与率)。
$$ 決定係数=1-\frac{\Sigma(y_i – \hat{y_i})^2}{\Sigma(y_i – \bar{y})^2} $$
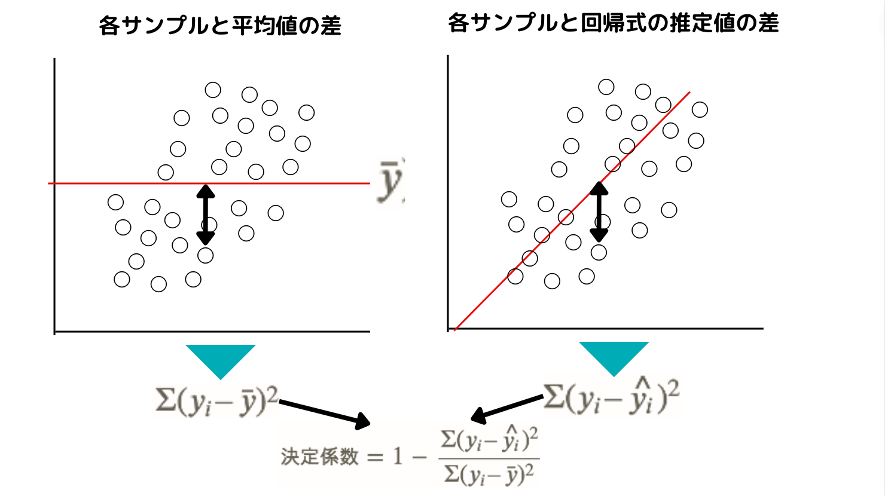
決定係数は、各サンプルの平均値との差の二乗を合計したものを分母として回帰式から得られた推定値との差の二乗を合計したものを分子としてそれを1から引いたものです。
0~1の値を取り1に近ければ近いほど回帰式のあてはまりが良いということになります。
これは図のように平均を引くだけシンプルなモデルと比較してどのくらい回帰式のあてはまりがよくなっているかを示す指標だと考えることができます。
分類精度:正解率

続いて分類タスク。
回帰タスクと違い分類タスクは「購入するか購入しないか」や、「不正か不正でないか」などの01の質的変数を予測するタスクのことを指します。
例えばクレジットカードの不正利用を判別したいとしましょう。
以下のようなマトリックスで表されます。
| 予測されたクラス | |||
| 異常 | 正常 | ||
| 実際のクラス | 異常 | a | b |
| 正常 | c | d | |
まず最も分かりやすいのが正解率(Accuracy)!
これは、
$$ Accuracy=\frac{a+d}{a+b+c+d} $$
で表します。
シンプルに全てのサンプルの中で実測値と予測値が一致した割合ですね。
以下のようになったとしましょう!
| 予測されたクラス | |||
| 異常 | 正常 | ||
| 実際のクラス | 異常 | 100 | 20 |
| 正常 | 80 | 800 | |
このような例だと正解率は900/1000=90%となります。
分類精度:適合率
他にもいくつか指標があります。
適合率(precision)は以下のように求めます。
$$ Precision=\frac{a}{a+c} $$
| 予測されたクラス | |||
| 異常 | 正常 | ||
| 実際のクラス | 異常 | a | b |
| 正常 | c | d | |
異常と予測されたクラスのうち実際に異常だったクラスの割合が適合率になります。
この場合は100/180=約56%になります。
分類精度:再現率
続いて、再現率(recall)!
再現率は以下のように求めます。
$$ recall=\frac{a}{a+b} $$
| 予測されたクラス | |||
| 異常 | 正常 | ||
| 実際のクラス | 異常 | a | b |
| 正常 | c | d | |
実際に異常だったクラスのうち、どのくらい異常と予測されたかです。
こちらは、100/120=83%となりました。
実は適合率と再現率はトレードオフの関係になります。
分類精度:F-measure
そしてそれら適合率と再現率を組みあわせて作られた指標がF-measureというものです。
F-measureは適合率と再現率の調和平均を取ります。
$$ F-measure=\frac{2}{\frac{1}{適合率}+\frac{1}{再現率}} $$
分類タスクにおける評価指標に関しては以下の記事でも詳しく解説しているのでチェックしてみてください!


機械学習の予測・分類精度評価ステップ
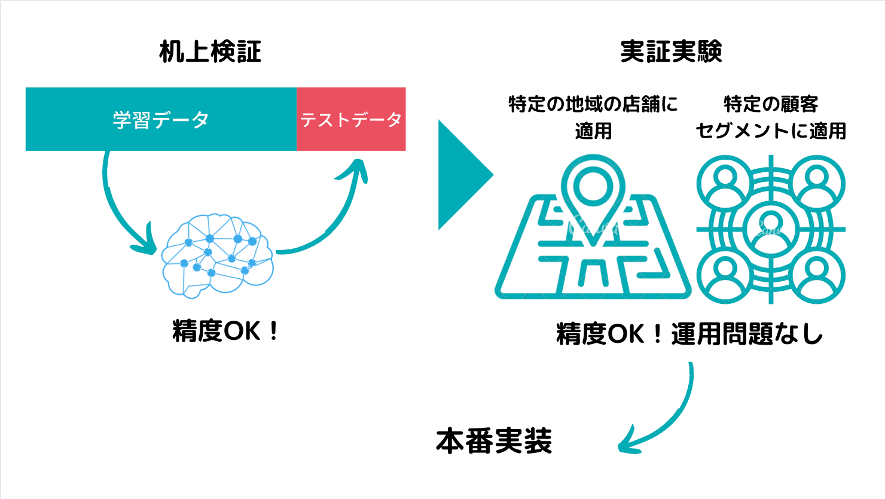
ここまででいくつかの評価指標について見てきましたが、実際にどのようにモデルを評価していくのでしょうか?
大きく分けて評価においては2つのステップがあります。
・机上検証における評価
・実際にテスト期間を設けての検証
机上検証における評価
作ったモデルにおいて既に持っているデータの中で机上検証を行うことは可能です。
例えば、現在が2021年4月だとして売上の需要予測をするのであれば2017年1月から2020年12月のデータを利用してモデルを構築し、そのモデルによって2021年1月〜3月の売上を予測することは可能です。
既に実測値も手元にあるので、どれくらいモデルの予測値との差があるか机上検証することが出来ます。
この場合は回帰タスクなので先程のMAEやRMSEなどを用いましょう。
もちろん分類タスクにおいても評価指標が変わるだけでプロセスは同じです。
実際にテスト期間を設けての検証
机上検証をおこなったとしても、同条件下でテスト期間を設けての現状のフローとの比較が必要になってきます。
売上予測なのであれば、実際に2021年4月以降のデータを予測してみて、現状の予測値との差を見てみる。
それで問題なさそうであれば運用に乗せて実装という方向に進んでいきます。
評価フェーズの注意点

さて、評価指標や評価ステップについて見てきましたが、最後に評価フェーズの注意点について確認しておきましょう!
過学習があると上手く評価できない
まずは、過学習という罠です。
過学習は別名「オーバーフィッティング」・「過適合」とかとも言ったりしますが、データ分析の分野では有名な罠です。
簡単に言うと、手元にあるデータだけにピッタリ合い未知データに対して全く合わないモデルを作ってしまうこと。
手元のデータだけ説明できても未知のデータを説明できるとは限らないんですね。
むしろ手元のデータに対してフィッティングし過ぎると未知データの予測精度は下がってしまいます。
データには必ずノイズ(誤差)が存在するため、完璧に当てることはほぼ不可能です。
完璧に当てようとするとノイズ自体にも適合したムダに複雑なモデルを作ってしまい、未知データには上手く当てはまらなくなってしまうのです。
過学習を防ぐためには学習モデルと検証データを分けてモデルを構築することが大事です。
疑似的に将来のデータを作り出すことで過学習を未然に防ぐモデル構築が行えるのです。
そしてこの学習データを検証データを分けて検証を行うことをバリデーションを呼びます。

実はバリデーションにはいくつかの方法があります。
以下の記事で詳しく解説しています。

また、過学習に関しては以下の記事でより詳しく解説しています。

不均衡データだと上手く評価できない
さらに分類タスクなのであれば、不均衡データという罠が生じる可能性があります。
不均衡データは2値分類なのであれば2つのサンプルデータに大きな差が生まれている状況を指します。
例えば先程のクレジットカードの例で以下のようになったとしましょう!
| 予測されたクラス | |||
| 異常 | 正常 | ||
| 実際のクラス | 異常 | 0 | 10 |
| 正常 | 0 | 990 | |
異常と正常が10:990なのでかなりの不均衡データになっていることが分かります。
この時、異常データは全く異常と予測出来ておらず、全て正常としてしまっているのですが、それでも正解率は990/1000=99%となることが分かります。
このように不均衡データになっていると、モデルが全く機能していないのに精度の評価は高く見えてしまうことになるのです。
これを回避するために不均衡データに対してはあらかじめ、オーバーサンプリングやアンダーサンプリングなどのサンプリング調整を行います。
以下の記事で不均衡データに対する対処法については詳しくまとめていますので是非チェックしてみてください!
せっかく評価結果がよくても業務フローに乗らない
また、せっかく評価結果がよくても業務フローに乗らないという問題があります。
これはCRISP-DMで言うビジネス理解の最初のフェーズである程度業務フローに乗せる時のイメージを現場とすりあわせておかないといけない問題なのですが、せっかくモデルを構築して検証しても業務フローに乗りませんということになりかねません。
例えば、1ヶ月前に予測がしたいのに、特徴量として1日前のデータをインプットしてしまっていたらそのモデルは業務に乗りません。
このように一見評価指標を見ると精度が高い!と思っても、業務フローに乗らないモデルになってしまっている可能性があるので注意が必要です。
機械学習の予測・分類精度における評価指標
本記事では、機械学習モデル構築における評価指標についてまとめてきました!
ぜひ評価指標の種類と評価のステップについて理解して使いこなせるようにしておきましょう!
以下の記事で機械学習の勉強法については詳しくまとめていますのであわせてチェックしてみてください!

また、ここで学んだ評価指標を実践で使っていくデータサイエンス全般を習得していくのであれば当メディアが運営する「スタアカ(スタビジアカデミー)」がオススメです!
世界最大小売業ウォルマートの実データを使って実践的な分析をしていきますよ!
ぜひチェックしてみてください!






















