こんにちは！
スタビジ編集部です！
今回は最小二乗法について解説していきます！
最小二乗法とは「データに一番よく合う直線や曲線を見つけるための方法」です。
これを使うと、たくさんの点（データ）の中で、それらの点に一番近い線を引くことができます。
この記事では、そんな最小二乗法の導出方法について解説していきます！
・最小二乗法の導出方法について解説！
以下のYoutube動画でも解説していますので合わせてチェックしてみてください！！
最小二乗法の導出方法について解説！
それでは具体的な事例で見ていきましょう！
たとえば、クラスの5人の友達で英語と数学のテストの点数の関係を調べたいとします。
5人の友達で英語と数学のテストの点数をグラフにプロットしてみることにしましょう。
しかし、みんなの点はバラバラで一つの線で完全には結べません。
そこで、最小二乗法を使うとこれらの点の「真ん中」を通るような直線を引くことができます。
これが「最も合っている直線」というわけです。
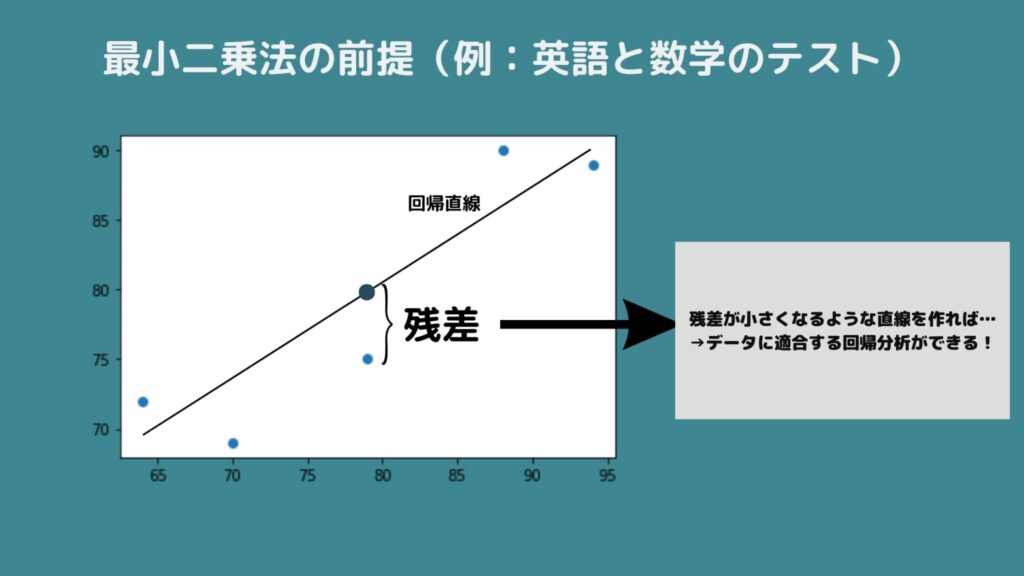
どうして「最も合っている」と言えるのかというと、各点から直線までの距離（これを「残差」といいます）の二乗（つまり、距離×距離）を合計したものが最小になる線を引くからです。
最小二乗法は「残差の平方和を最小にする方法」であり、これによって尤もらしい直線を表せるパラメータを導出することができるわけですね！
問題設定（単回帰分析の場合）
ここからちょっと数式をまじえて見ていきましょう！
実際に最小二乗法の問題設定を見ていきましょう！
最小二乗法は変数が大量にある多変数問題でも使えるのですが、ここではシンプルな単変数において単回帰分析を行いたいケースで数式展開をしていきましょう！
\(y_{i}\)は目的変数、\(x_{i}\)は説明変数、\(\hat{y_{i}}\)は予測値とすると残差平方和は以下のようになり、この式を最小化する\(β_{0}\)と\(β_{1}\)を見つけたいということになります。
\(E=\sum_{i=1}^{n}(y_{i}-(β_{0}+β_{1}x_{i}))^{2}\)
回帰式は\(β_{0}+β_{1}x_{i}\)で表されているので、回帰式で算出した予測値と観測値であるデータ\(y_{i}\)の差を2乗したものを合計していることがわかります。
これこそが残差平方和なのです。
繰り返しになりますが、最小二乗法のゴールは単回帰モデルにおけるパラメータ\(\hat{β_{0}}, \hat{β_{1}}\)を導出することです。
したがって先ほどの問題設定を\(β_{0}, β_{1}\)のそれぞれで偏微分してみましょう。偏微分した式が0になるパラメータが残差平方和を最小にする最適なパラメータになることが知られています。
\(\frac{δE}{δβ_{0}}=-2\sum_{i=1}^{n}(y_{i}-β_{0}-β_{1}x_{i})\)
\(\frac{δE}{δβ_{1}}=-2\sum_{i=1}^{n}(y_{i}-β_{0}-β_{1}x_{i})x_{i}\)
これらの式を0としたとき、式展開することができます。
左辺に0を代入して、そのまま左辺に項を移せばいいので簡単ですね！以下のようになります。
\(\sum_{i=1}^{n}y_{i} = nβ_{0}+\sum_{i=1}^{n}β_{1}x_{i}\)
\(\sum_{i=1}^{n}x_{i}y_{i} = \sum_{i=1}^{n}β_{0}x_{i}+\sum_{i=1}^{n}β_{1}x_{i}^{2}\)
それでは、これらの式を展開していきましょう！まず最初の式を展開すると…
\(nβ_{0}=\sum_{i=1}^{n}y_{i}-\sum_{i=1}^{n}β_{1}x_{i}\)
\(β_{0}=\frac{1}{n}\sum_{i=1}^{n}y_{i}-β_{1}\frac{1}{n}\sum_{i=1}^{n}x_{i}\)
\(β_{0} = \bar{y}-β_{1}\bar{x}\)
この式を使って、先ほどの2番目の式に代入しつつ計算すると…少し複雑ですが以下のように展開することができ
\(\sum_{i=1}^{n}x_{i}y_{i} = \sum_{i=1}^{n}(\bar{y}-β_{1}\bar{x})x_{i}+\sum_{i=1}^{n}β_{1}x_{i}^{2}\)
\(\sum_{i=1}^{n}x_{i}y_{i} = (\bar{y}-β_{1}\bar{x})n\bar{x}+\sum_{i=1}^{n}β_{1}x_{i}^{2}\)
\(\sum_{i=1}^{n}x_{i}y_{i} = n\bar{x}\bar{y}-nβ_{1}\bar{x}^{2}+β_{1}\sum_{i=1}^{n}x_{i}^{2}\)
\(\sum_{i=1}^{n}x_{i}y_{i} – n\bar{x}\bar{y} = β_{1}(\sum_{i=1}^{n}x_{i}^{2}-n\bar{x}^{2})\)
最終的に\(β_{1}\)を求めると以下の式ができますね！
\(β_{1}=\frac{\frac{1}{n}\sum_{i=1}^{n}x_{i}y_{i} – \bar{x}\bar{y}}{\frac{1}{n}\sum_{i=1}^{n}x_{i}^{2}-\bar{x}^{2}}\)
次に\(\frac{1}{n}\sum_{i=1}^{n}x_{i}^{2}-\bar{x}^{2}\)を変形しましょう。
\(\frac{1}{n}\sum_{i=1}^{n}x_{i}^{2}-\bar{x}^{2}=\frac{1}{n}\sum_{i=1}^{n}x_{i}^{2}-2\bar{x}^{2}+\bar{x}^{2}=\)
\(\frac{1}{n}\sum_{i=1}^{n}x_{i}^{2}-2\frac{\sum_{i=1}^{n}x_{i}}{n}\bar{x}+\bar{x}^{2}=\frac{1}{n}\sum_{i=1}^{n}(x_{i}^{2}-2\bar{x}x_{i}+n\bar{x}^{2})=\)
\(\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}\)
そして\(\frac{1}{n}\sum_{i=1}^{n}x_{i}y_{i} – \bar{x}\bar{y}\)を式展開しましょう。
\(\frac{1}{n}\sum_{i=1}^{n}x_{i}y_{i} – \bar{x}\bar{y}=\frac{1}{n}\sum_{i=1}^{n}x_{i}y_{i} – 2\bar{x}\bar{y}+\bar{x}\bar{y}=\)
\(\frac{1}{n}(\sum_{i=1}^{n}x_{i}y_{i}-2nx_{i}y_{i}+nx_{i}y_{i})=\frac{1}{n}\sum_{i=1}^{n}(x_{i}y_{i}-\bar{x_{i}}y_{i}-x_{i}\bar{y_{i}}+\bar{x}\bar{y})=\)
\(\frac{1}{n}\sum_{i=1}^{n}((x_{i}-\bar{x})(y_{i}-\bar{y}))\)
式展開した2つの式を、先ほどの式に代入すると…
\(β_{1}=\frac{\sum_{i=1}^{n}(x_{i}-\bar{x})(y_{i}-\bar{y})}{\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}}=\frac{S_{xy}}{S_{x}^{2}}\)
\(β_{1}\)は\(x\),\(y\)の共分散\(S_{xy}\)を\(x\)の分散\(S_{x}\)で除した値であることが分かります。
まとめると単回帰式におけるパラメータは以下の通りです！
\(β_{0} = \bar{y}-β_{1}\bar{x}\)
\(β_{1}=\frac{\sum_{i=1}^{n}(x_{i}-\bar{x})(y_{i}-\bar{y})}{\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}}\)
Pythonで見てみよう！
先程のデータを用いて\(β_{1}\)の計算が合っているかを確認していきましょう。
sklearn.linear_modelのLinearRegressionから求めた回帰係数\(β_{1}\)と共分散と分散から求めた回帰係数を比較していきます。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
x = pd.DataFrame([88,64,79,94,70])
y = pd.DataFrame([90,72,75,89,69])
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(x,y)
print("計算した回帰係数:{}".format(np.cov([[88,64,79,94,70],[90,72,75,89,69]],bias=True)[0,1]/np.var([88,64,79,94,70])))
print("切片:{},回帰係数:{}".format(model.intercept_,model.coef_))
計算した回帰係数はモジュールで求めた回帰係数と一致しているため、最小二乗法による回帰係数の求め方は合っていることが分かりましたね！
最小二乗法 まとめ
本記事では最小二乗法についてまとめました！
今回は回帰分析を使ったので、どのような手法なのか知りたい方はこちらもご覧ください！
また重回帰分析における回帰係数の求め方について詳しく書かれた記事もあるので、ぜひ参照してください！
このようなデータサイエンスの力を身に付けるためにはスタビジの記事やスクールを活用すると良いでしょう。
当メディアでは、データサイエンティストの経験を詰め込んだデータサイエンス特化のスクール「スタアカ（スタビジアカデミー）」を運営していますので，興味のある方はぜひチェックしてみてください！
AIデータサイエンス特化スクール「スタアカ」
| 【価格】 | ライトプラン：1280円/月 プレミアムプラン：149,800円 |
|---|---|
| 【オススメ度】 | |
| 【サポート体制】 | |
| 【受講形式】 | オンライン形式 |
| 【学習範囲】 | データサイエンスを網羅的に学ぶ 実践的なビジネスフレームワークを学ぶ SQLとPythonを組み合わせて実データを使った様々なワークを行う マーケティングの実行プラン策定 マーケティングとデータ分析の掛け合わせで集客マネタイズ |
データサイエンティストとしての経験をふまえてエッセンスを詰め込んだのがこちらのスタビジアカデミー、略して「スタアカ」！！
当メディアが運営するスクールです。
24時間以内の質問対応と現役データサイエンティストによる複数回のメンタリングを実施します！
カリキュラム自体は、他のスクールと比較して圧倒的に良い自信があるのでぜひ受講してみてください！
他のスクールのカリキュラムはPythonでの機械学習実装だけに焦点が当たっているものが多く、実務に即した内容になっていないものが多いです。
そんな課題感に対して、実務で使うことの多いSQLや機械学習のビジネス導入プロセスの理解なども合わせて学べるボリューム満点のコースになっています！
Pythonが初めての人でも学べるようなカリキュラムしておりますので是非チェックしてみてください！
ウォルマートのデータを使って商品の予測分析をしたり、実務で使うことの多いGoogleプロダクトのBigQueryを使って投球分析をしたり、データサイエンティストに必要なビジネス・マーケティングの基礎を学んでマーケティングプランを作ってもらったり・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践してもらったりする盛りだくさんの内容になってます！
・BigQuery上でSQL、Google Colab上でPythonを使い野球の投球分析
・世界最大手小売企業のウォルマートの実データを用いた需要予測
・ビジネス・マーケティングの基礎を学んで実際の企業を題材にしたマーケティングプランの策定
・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践して稼ぐ
データサイエンスに関する記事はこちら！
データサイエンスを勉強できるスクールやサイトは、ぜひこちらを参考にしてみてください！
スタビジのコンテンツをさらに深堀りしたコンテンツが動画と一緒に学べるスクールです。
プレミアムプランでは私がマンツーマンで伴走させていただきます！ご受講お待ちしております！
