統計的検定とは?具体例と種類について見ていこう!

アカデミックの世界でもビジネスの世界でも、ある事象に対して仮説を検証する時には必ず統計的検定を行います。
統計的検定を行わず、数値をただ比較して差がありそうだねと結論付けてしまうのは、あまりにも安直。
そんな統計学の中で非常に基礎でありながら重要な統計的検定について説明していきたいと思います。
以下の動画でも分かりやすく解説しているので、ぜひ見てみてください!
統計的検定ってなに?
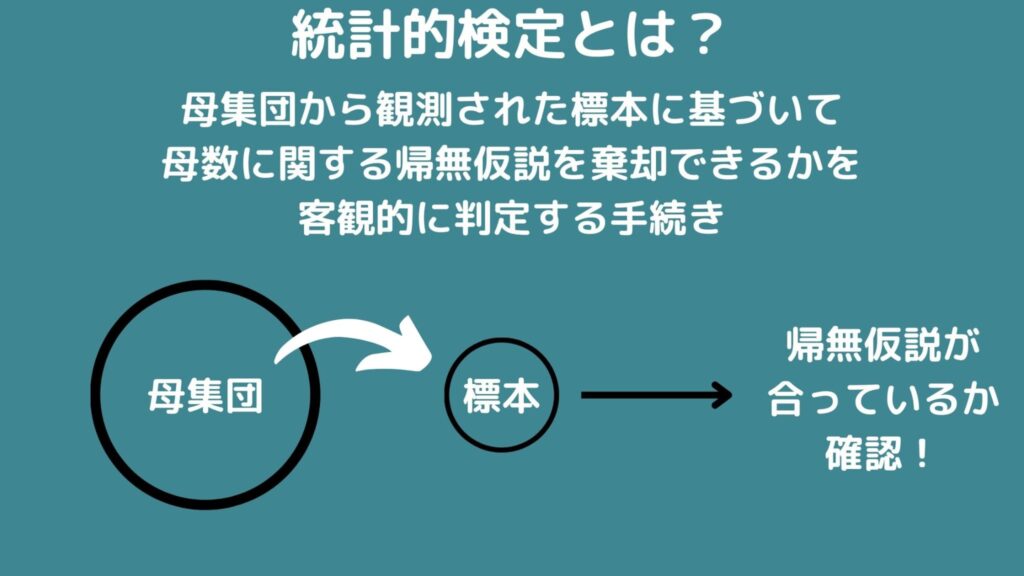
統計的検定は統計学を初めて学ぶ人にも早いうちに出てくる分野です。

統計学の中では基礎ですが、非常に深くて重要なテーマです。
ここでは、”一般的な”検定であるネイマン流の頻度論に基づく検定についてなるべく分かりやすく紹介します。
細かな検定の種類や計算方法ではなく、検定や推定がどのような考えなのかを分かりやすく伝えることを目的としています。
統計的検定はどんなときに使う?

統計的検定を用いる状況として、例えばアイス製造会社を考えてみましょう。
この会社が製造しているバニラアイスの内容量は200mlに設定しているはずです。
ある日、社長が「200mlになっていない気がする」と生産管理の担当者に伝えました。そこで、生産管理の担当者であるAさんとBさんは本当に200mlになっているかどうかを確かめることにしました。そして、製造した製品の中から無作為に10個ほど選んで内容量を測ったところ次のようになりました。
$$205,198,197,208,204,202,207,199,207,203 (ml)$$
このデータから平均値を計算すると\(\bar{x}=203\)でした。さて、設定は200mlからずれているのでしょうか。
そう、統計的検定はこのように人によって判断が変わりそうな微妙な事象を数理的に判断できる便利な手法なのです!
統計的検定に関する用語

ここで、具体例と照らしあわせて用語を整理します。
・母集団…ある傾向をもつアイスの集まり。(神にしか分からない)
・母数…母集団の特徴を定める傾向のこと。例えば、母平均や母分散。(神にしか分からない)
・標本…母集団から得られた観測値群のこと。今の場合、選んだアイス10個のこと。
・帰無仮説…何も違いがないという仮説。今の場合、「アイスの平均の設定が200mlでずれていない」ということ。
・対立仮説…何か違いがあるという仮説。今の場合、「アイスの平均の設定が200mlからずれている」ということ。
・棄却…帰無仮説を否定すること
ここで出てくる用語は覚えておきましょう!
統計的検定の流れ

では、実際に統計的検定の流れを説明して行きます。
検定では確率分布という道具を使います。
今回の場合はアイスの平均に関する検定なので正規分布を用います。
また、簡単のために母分散は\(4^2\)と知っていることにしておきます。そうすると母集団は\(N(\mu,4^2)\)に従います。そして、問題は\(\mu\)が200であるのかどうなのかということです。
仮に、\(\mu=200\)であるとしましょう。平均\(\bar{x}=203\)を正規化した\(u\)は\(N(0,1^2)\)に従います。
このとき、正規分布の確率密度関数から分布の端っこの面積が5%になる点はどこかを計算すると-1.960と1.960という値になります。
これはつまり\(N(0,1^2)\)に従うデータが「-1.960よりも小さい」あるいは「1.960よりも大きい」可能性が5%くらいしかあり得ないということを意味します。
さて、いま計算して\(|u|\)を求めると2.372という値になりました。この値は1.960より大きいです。どう思いますか?
確率分布に正規分布を用いましたが、正規分布以外を用いることもたくさんあります。
どんな分布を使うかはデータの種類や形式、検定したい母数の種類によって変わります。
しかし、検定の基本的な流れはどんな場合でも変わりません。
今回の説明が統計的検定というものの理解の助けになれば幸いです。
また、区間推定(95%信頼区間)の考え方もとても参考になります!
以下で分かりやすくまとめているのでぜひチェックを!

統計的検定の種類

この記事では単純な仮説検定について見てきましたが、統計的検定にはいくつかの種類があります。
それぞれの特徴について見ていきましょう!
押さえておきたい統計的検定の種類は以下の3つ!
F検定を使う場面はあまりないかも!
・t検定
・カイ二乗検定
・F検定
t検定
t検定は、母平均の検定に用いられます。つまり先ほどの例はt検定の一種。
しかしt検定とは言えどもいくつかの種類があるのです。ここで紹介したt検定は最も一般的な統計的検定であり、1標本のt検定と呼ばれます。
1つのサンプルデータが元々想定されている母平均と比較してズレているかを検定しています。
これ以外にも2つの標本の母平均を比較する2標本のt検定も存在しますし、回帰分析の回帰係数にもt検定が用いられているのです。
t検定について詳しくは以下の記事にまとめています!

カイ二乗検定
カイ二乗検定は、ビジネスシーンで使われることの多い検定手法になります。
カイ二乗検定では一般的に分布の乖離度を測るものでありABテストにて用いられることが多いです。
例えば、メールを送り以下のような結果が得られたとします。その時メールABの開封率には有意差がありますでしょうか?
| 送信数 | 開封数 | 開封率 | |
| メールA | 100000 | 12000 | 12% |
| メールB | 200 | 30 | 15% |
開封率だけ見るとありそうですが、どうでしょう?それを数理的に証明するのがカイ二乗検定なのです。
実際この場合、数理的に有意差があるとは言えません。
カイ二乗検定については以下の記事で詳しくまとめています。

ちなみにABテストをカイ二乗検定で行う有意差アプリケーションを作る方法を以下の記事にまとめていますのでよければご覧ください!
F検定
F検定は、t検定やカイ二乗検定と比較すると登場する場面が少ないのですが、t検定を行う前手の検定として行う場合があります。
F検定では、母分散の検定を行います。
t検定では、母分散が等しいと仮定して検定を行うためF検定を行い母分散が果たして正しいのか確認する場合があります。
統計的検定 まとめ
統計的検定についてまとめてきました!
基本的には、t検定とカイ二乗検定さえ押さえておけば問題ありません。
簡単にExcel、R、Pythonで実装も出来ますし、ネットで調べれば数値を入力するだけで解答してくれる便利なツールもあります。
統計の勉強にはPythonが非常に便利!

ぜひチェックしてみてください!
また当メディアで展開するスタアカではt検定やカイ二乗検定の具体的な実装方法を具体例を混じえながら学べます。
ご受講お待ちしております!
統計的検定においては以下の記事がオススメです。是非ご覧ください!
統計を最初から勉強する上で持っておきたい良書です。検定について詳しく載っています。
統計的検定をふまえた上でさらに統計学について学びたいという方は以下の記事をご覧ください。
統計学を学ぶステップをまとめています!

























